Funzione continua

La funzione in rosso è continua, quella in blu non lo è

In matematica, una funzione continua è una funzione che, intuitivamente, fa corrispondere a elementi sufficientemente vicini del dominio elementi arbitrariamente vicini del codominio.

Esistono diverse definizioni di continuità, corrispondenti ai contesti matematici in cui vengono utilizzate: la continuità di una funzione è uno dei concetti di base della topologia e dell'analisi matematica. La continuità di una funzione può essere definita anche in modo locale: in questo caso si parla di continuità in un punto del dominio. Una funzione continua è, per definizione, continua in ogni punto del proprio dominio. Una funzione che non è continua è detta discontinua, e i punti del dominio in cui non è continua sono detti punti di discontinuità.

Per esempio, la funzione $h(t)$ che descrive l'altezza di un uomo rispetto alla sua età può essere vista come una funzione continua: in periodi brevi l'uomo cresce di poco. Al contrario, la funzione $g(t)$ che rappresenta la quantità di denaro presente in un conto corrente nel tempo è una funzione discontinua, poiché prelievi e depositi le fanno fare salti da un valore all'altro.

Definizioni

La continuità di una funzione è un concetto topologico, e quindi la definizione generale di funzione continua si sviluppa con funzioni tra spazi topologici. Lo stesso concetto è però usato in ambiti meno generali, soprattutto per quanto riguarda il suo utilizzo in analisi matematica: è spesso presentata la definizione di continuità solo per funzioni tra spazi metrici, o ancora, solo per funzioni di una variabile reale.

Funzioni reali

Il grafico della funzione presenta un salto in x₀: la funzione non è continua

Nel caso di funzioni di una variabile reale, spesso la continuità è presentata come una proprietà del grafico: la funzione è continua se il suo grafico è formato da un'unica curva che non compia mai salti. Sebbene questa nozione possa essere usata nei casi più semplici per distinguere funzioni continue da funzioni discontinue, non è formalmente corretta, e può portare ad ambiguità o errori.

Definizione in termini di limite di una funzione

Una funzione $f$ si definisce continua nel punto $p$ del suo dominio se il suo limite per $x$ tendente a $p$ coincide con la valutazione della funzione in $p$, ovvero con $f(p)$. In simboli:

$\lim _{x\to p}f(x)=f(p)$

Tale definizione è usata maggiormente per funzioni definite su un intervallo della retta reale: infatti, essa ha senso solo se $p$ è un punto di accumulazione per il dominio di $f$. Essa è comunque estendibile anche nel caso di domini più complicati, che comprendono punti isolati: in essi, $f$ risulta continua per una "verità vuota" (dall'inglese vacuous truth).

La funzione si dice continua se è continua in ogni punto $p$ del dominio.

Definizione epsilon-delta

Studiando la funzione nel punto $p=2$, e scegliendo $\varepsilon =0.5$, basta scegliere $\delta =0.5$ per far sì che tutte le immagini dei punti in $(2-\delta ,2+\delta )$ distino per meno di $\epsilon$ da $f(2)=3.5$

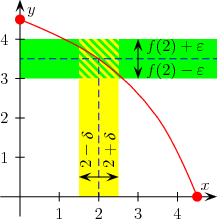
Una funzione $f\colon A\rightarrow \mathbb {R}$ definita su un sottoinsieme $A$ dei numeri reali a valori reali si dice continua in un punto $p\in A$ se per ogni numero $\varepsilon >0$, arbitrariamente piccolo, esiste un secondo numero $\delta >0$ tale che, $\forall x\in A\cap (p-\delta ,p+\delta )$, la funzione $f(x)$ dista da $f(p)$ per meno di $\varepsilon$, ovvero:

$|f(x)-f(p)|<\varepsilon$

In linguaggio simbolico, una funzione è continua in un punto $p$ se:

$\forall \varepsilon >0\ \exists \delta >0:|x-p|<\delta \Rightarrow |f(x)-f(p)|<\varepsilon$

Se questa proprietà vale per ogni punto nel dominio di definizione della funzione, allora si dice che la funzione è continua. In questo caso si dice che $f(x)\in C(A,\mathbb {R} )$, che è l'insieme delle funzioni continue a valori reali e variabili in $A$.

Più intuitivamente, se si vuole che la funzione $f(x)$ disti di un valore piccolo da $f(p)$ ci basta restringerci ad un intorno abbastanza piccolo del punto $p$. Se questo è possibile qualunque sia la distanza scelta (a meno di restringere ulteriormente l'intorno di $p$), allora la funzione è continua in $p$.

Questa definizione è equivalente a quella data in precedenza: essa è costruita dalla prima semplicemente esplicitando la definizione di limite di una funzione. È stata usata per la prima volta da Cauchy.

Funzioni tra spazi topologici

f è continua in un punto x ∈ X se (e solo se) per ogni intorno V di f(x) esiste un intorno U di x tale che f(U) ⊆ V. Intuitivamente, per quanto sia piccolo V esiste sempre un U contenente x che viene mappato in V.

La definizione di continuità data nel caso di funzioni reali può essere generalizzata in contesti più ampi, come quello degli spazi topologici.

Siano due spazi topologici $(X,\tau _{1})$, $(Y,\tau _{2})$ e sia $f:X\to Y$ un'applicazione. Allora:

$f$ si dice continua in $x_{0}\in X$ se $\forall \ V$ intorno di $f(x_{0})$ $\exists \ U$ intorno di $x_{0}$ tale che $f(U)\subseteq V$;

$f$ si dice continua se $\forall \ A$ aperto in $Y$ $f^{-1}(A)=\{x\in X|f(x)\in A\}$ è un insieme aperto in $X$.

Osserviamo che altre definizioni equivalenti di funzione continua sono:

• $f$ è continua in ogni punto $x\in X$;
• $\forall \ B\in \Gamma$ $f^{-1}(B)$ è aperto in $X$ con $\Gamma$ una base della topologia $\tau _{2}$;
• $\forall \ P\in \Pi$ $f^{-1}(P)$ è aperto in $X$ con $\Pi$ una prebase della topologia $\tau _{2}$;
• $\forall \ C$ chiuso in $Y$ $f^{-1}(C)$ è chiuso in $X$;
• $\forall \ T\subseteq Y$ $Cl(f^{-1}(T))\subseteq f^{-1}(Cl(T))$ con $Cl$ la chiusura di un sottoinsieme;
• $\forall \ S\subseteq X$ $f(Cl(S))\subseteq Cl(f(S))$ con $Cl$ la chiusura di un sottoinsieme.

La definizione di continuità è strettamente legata alla topologia scelta nel dominio e nel codominio: funzioni continue con alcune scelte di topologia possono non esserlo con altre. Per esempio, la funzione identità è continua se lo spazio di arrivo ha la stessa topologia dello spazio di partenza, oppure se ne ha una meno fine, ovvero con meno aperti. Se invece lo spazio di arrivo ha una topologia più fine, con più aperti, la funzione identità non risulta continua.

Funzioni tra spazi metrici

Gli spazi metrici sono spazi topologici nei quali la topologia è generata da una base di intorni circolari. Sia $f$ una funzione tra due spazi metrici $(X,d_{1})$ e $(Y,d_{2})$. La funzione f si dice continua in un punto $p$ se, per ogni scelta di $\varepsilon >0$, esiste un $\delta >0$, tale che, per ogni punto $x\in X$ che dista meno di $\delta$ da $p$, ovvero che:

$d_{1}(x,p)<\delta$

si ha che $f(x)$ dista per meno di $\varepsilon$ da $f(p)$, ovvero:

$d_{2}(f(x),f(p))<\varepsilon .$

La definizione può essere scritta servendosi della nozione di intorno sferico $B_{r}(p)$ centrato in $p$, di raggio $\delta$: in questo caso, la funzione è continua se $x\in B_{\delta }(p)\cap E$ implica che $f(x)\in B_{\varepsilon }(f(p))$ o, simbolicamente:

$\forall \varepsilon >0\quad \exists \delta >0:f(E\cap B_{\delta }(p))\subset B_{\varepsilon }(f(p)),$

dove $E$ è l'insieme di definizione di $f$.

Nel caso di funzioni reali, le definizioni coincidono se le due distanze su dominio e codominio non sono altro che il modulo della differenza tra due valori in $\mathbb {R}$.

Inoltre, questa definizione è valida per funzioni definite e a valori in tutti gli spazi vettoriali normati, dove la distanza sia la norma della differenza tra due punti. In particolare, è valida in $\mathbb {R} ^{n}$ con la norma euclidea, ed estende quindi la definizione di continuità a funzioni di più variabili.

Esempi

Una funzione cubica, espressa da un polinomio di terzo grado, è una funzione continua.

Sono esempi di funzioni continue:

• Le funzioni costanti $f(x)=c$.
• La funzione identità $f(x)=x$ da uno spazio topologico $(X,\tau _{1})$ allo stesso spazio $(X,\tau _{2})$, dove $\tau _{2}$ è la stessa topologia del dominio oppure una topologia meno fine.
• Le funzioni che associano ad una coppia di numeri $(x,y)$ la somma $x+y$, il prodotto $xy$ o il rapporto $x/y$ sono continue nel loro insieme di definizione in $\mathbb {R} ^{2}$.
• Le trasformazioni lineari fra spazi euclidei
• Le funzioni espresse da polinomi, come per esempio $f(x)=x^{3}+2x^{2}-3x+2$.
• Le funzioni razionali, in tutti i punti in cui sono definite, ovvero in tutti i punti in cui non si annulla il denominatore.
• La funzione esponenziale e il logaritmo naturale nei loro insiemi di definizione, ovvero $f(x)=\exp(x)$ e $f(x)=\log(x)$.
• Le funzioni seno e coseno, ovvero $f(x)=\cos(x)$ e $f(x)=\sin(x)$.
• La funzione valore assoluto $f(x)=|x|$ è continua (ma non derivabile in $x=0$).
• La funzione di Cantor e la curva di Koch sono esempi di funzioni continue con struttura frattale.
• La curva di Peano: una curva piana che ricopre l'intero quadrato.
• La funzione $f(x)=x^{x}$ nel suo dominio reale. Essa è definita e continua per ogni $x>0,$ e per valori di $x$ negativi interi e razionali con denominatore dispari.

La funzione di Heaviside presenta una discontinuità in 0.

Sono esempi di funzioni non continue:

• La funzione di Heaviside, definita come

$H(x)={\begin{cases}1&{\text{se }}x\geq 0\\0&{\text{se }}x<0.\end{cases}}$

• La funzione indicatrice di un sottoinsieme proprio di $\mathbb {R}$ è discontinua sulla frontiera dell'insieme.
• La funzione di Dirichlet è discontinua in ogni punto.

Proprietà delle funzioni continue

Sia $f\colon I\to \mathbb {R}$ una funzione continua a valori reali definita su un intervallo $I$. Valgono:

• Permanenza del segno: Se in un punto $p$ del suo dominio $f(p)>0$, allora esiste un intorno $U(p)$ tale che $f(x)>0$ in tutti i punti dell'intorno.
• Teorema dei valori intermedi: se $a$ e $b$ sono due punti del dominio, allora $f$ assume tutti i valori compresi fra $f(a)$ e $f(b)$.
• Teorema di Bolzano: se $a$ e $b$ sono due punti del dominio tali che $f(a)\cdot f(b)\,<\,0$ (ovvero se $f(a)$ e $f(b)$ hanno segno diverso), allora esiste almeno un $p\in (a,b)$ tale che $f(p)=0.$
• Teorema di Weierstrass: se l'intervallo $I$ è chiuso e limitato, ovvero se $I=[a,b]$, allora $f$ ammette massimo e minimo, ovvero esistono due punti $p$ e $q$ tali che $f(p)\leq f(x)\leq f(q)$ per ogni $x\in [a,b]$.

Se $f$ è una funzione continua biiettiva a valori reali definita su un intervallo, allora $f$ è strettamente monotona e la funzione inversa $f^{-1}$ è continua e strettamente monotona. L'implicazione non vale in generale per le funzioni il cui dominio non è un intervallo.

Sia $f\colon (X,d_{1})\to (Y,d_{2})$ una funzione tra spazi metrici. Valgono:

• Teorema di Weierstrass: se $X$ è un insieme compatto, allora $f$ assume massimo e minimo in $X$. In particolare esistono $p,q\in X$ tali che $f(p)\leq f(x)\leq f(q)$ per ogni $x\in X$.
• Se $f$ è biunivoca e $X$ è compatto, allora $f^{-1}$ è continua.
• Teorema di Heine - Cantor: se $X$ è compatto, allora $f$ è uniformemente continua.
• Se $f(x)=(f_{1}(x),\dots ,f_{n}(x))$, allora $f$ è continua se e solo se è continua ogni funzione $f_{i}(x)$. Questo risultato è valido quindi per le funzioni $f(x):\mathbb {R} \to \mathbb {R} ^{n}$.

Sia $f\colon (X,\tau _{1})\to (Y,\tau _{2})$ una funzione continua tra spazi topologici. Valgono:

• La controimmagine di un insieme aperto è un insieme aperto. Non è vero in generale che l'immagine di un insieme aperto sia un insieme aperto.
• La controimmagine di un insieme chiuso è un insieme chiuso.
• L'immagine di un insieme compatto è un insieme compatto.
• L'immagine di un insieme connesso è un insieme connesso.
• L'immagine di un insieme connesso per archi è un insieme connesso per archi.

Composizione

La composizione di funzioni continue è una funzione continua, ovvero se $f$ e $g$ sono due funzioni continue, allora anche:

$h(x)=(f\circ g)(x)=f(g(x))$

è una funzione continua.

Come conseguenza di questa proprietà si hanno le seguenti:

• La somma $f+g$ di due funzioni continue è una funzione continua.
• Il prodotto $f\cdot g$ di due funzioni continue è una funzione continua.
• Il quoziente $f/g$ di due funzioni continue è una funzione continua (nell'insieme di definizione, ovvero dove $g$ è diversa da 0).

In generale, l'inverso non è vero: ad esempio, se una funzione continua è somma di due funzioni, non è detto che entrambi gli addendi siano a loro volta funzioni continue. Ad esempio se

$f(x)={\begin{cases}0\quad {\text{se }}x\neq 1\\1\quad {\text{se }}x=1\end{cases}}\quad {\text{e}}\quad g(x)={\begin{cases}1\quad {\text{se }}x\neq 1\\0\quad {\text{se }}x=1\end{cases}},$

allora $f$ e $g$ non sono continue, ma

$f(x)+g(x)=1\quad {\text{e}}\quad f(x)g(x)=0$

sono entrambe continue su tutto $\mathbb {R}$. Analogamente se

$f(x)={\begin{cases}3\quad {\text{se }}x\neq 1\\9\quad {\text{se }}x=1\end{cases}}\quad {\text{e}}\quad g(x)={\begin{cases}1\quad {\text{se }}x\neq 1\\3\quad {\text{se }}x=1\end{cases}},$

allora $f$ e $g$ non sono continue, ma

${\frac {f(x)}{g(x)}}=3$

è continua su tutto $\mathbb {R}$.

Successioni

L'animazione mostra una sequenza di funzioni continue che converge puntualmente a una funzione discontinua

Data una successione di funzioni continue $f_{1},f_{2},\dotsc \colon I\to \mathbb {R}$ tali che il limite:

$f(x):=\lim _{n\to \infty }f_{n}(x)$

esiste finito per ogni $x\in \mathbb {R}$ (convergenza puntuale), allora non è necessariamente vero che $f(x)$ è una funzione continua. Se però la successione converge uniformemente, allora il limite puntuale $f(x)$ è continuo.

Derivazione e integrazione

Una funzione derivabile (o più in generale una funzione differenziabile) in un punto $p$ è sempre continua in quel punto. Non è vero l'inverso: esistono funzioni continue non derivabili, come ad esempio la funzione valore assoluto, continua in $0$ ma non derivabile nello stesso punto. Esistono anche funzioni a variabile reale continue in tutti i punti del dominio e non derivabili in nessuno di essi, come la funzione di Weierstrass.

Una funzione continua $f\colon [a,b]\rightarrow \mathbb {R}$ è sempre integrabile secondo Riemann (e quindi anche secondo Lebesgue). Inoltre, $f$ ammette sempre primitive e ogni sua primitiva è continua. Viceversa, non tutte le funzioni integrabili sono continue: per esempio, sono integrabili tutte le funzioni costanti a tratti.

Altri tipi di continuità

Continuità per successioni

Una funzione $f$ a valori reali è continua per successioni in $x_{0}$ se, per ogni successione $x_{n}$ a valori nel dominio della funzione e convergente a $x_{0}$, la successione $f(x_{n})$ converge a $f(x_{0})$.

Questa formulazione di continuità è dovuta ad Eduard Heine.

Una funzione continua è sempre continua per successioni, mentre, al contrario è possibile dare esempi di funzioni continue per successioni, ma non continue. L'inverso vale solo se il dominio $\scriptstyle {X}$ è uno spazio sequenziale, come lo sono gli spazi primo-numerabili e dunque in particolare gli spazi metrici: in questo caso, quindi, le due definizioni si possono considerare equivalenti.

Continuità a sinistra e a destra

Una funzione continua a destra

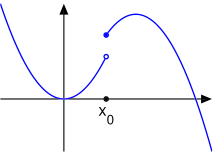
Una funzione reale $f$ si dice continua a destra in $x_{0}$ se:

$\lim _{x\to x_{0}^{+}}f(x)=f(x_{0}),$

dove il limite è inteso solo come limite destro.

Una funzione $f$ si dice continua a sinistra in $x_{0}$ se:

$\lim _{x\to x_{0}^{-}}f(x)=f(x_{0}).$

Una funzione è continua in un punto se e solo se è ivi continua a destra e a sinistra.

Queste proprietà non sono estendibili a funzioni a più di una variabile, in quanto nel piano, nello spazio, e generalmente in $\mathbb {R} ^{n}$ quando $n>1$ non esiste relazione d'ordine, ovvero non è possibile definire una "destra" o una "sinistra".

Semicontinuità

Una funzione semicontinua inferiormente: nel punto di salto, $f(x_{0})$ si trova in basso

Una funzione $f$ definita su uno spazio topologico $X$ a valori reali si dice semicontinua inferiormente in $x_{0}\in X$ se per ogni $\varepsilon >0$ esiste un intorno $U$ di $x_{0}$ tale che per ogni $x\in U$, si ha:

$f(x)>f(x_{0})-\varepsilon .$

Se invece vale, per ogni $x\in U$:

$f(x)<f(x_{0})+\varepsilon$

la funzione viene detta semicontinua superiormente in $x_{0}$.

Se la prima (o rispettivamente la seconda) proprietà vale in ogni punto del dominio, si dice che la funzione è semicontinua inferiormente (o rispettivamente semicontinua superiormente).

La semicontinuità (sia inferiore che superiore), è una proprietà più debole della continuità: esistono funzioni semicontinue ma non continue. Viceversa, una funzione è continua se e solo se è sia semicontinua inferiormente che semicontinua superiormente.

Continuità separata

Nel caso di funzioni di più variabili, è possibile definire una condizione più debole di continuità, detta continuità separata: una funzione $f$ è continua separatamente in un punto $p$ rispetto a una delle variabili $x_{i}$ se è continua la funzione di una variabile dipendente solo dal parametro $x_{i}$, lasciando le restanti variabili fissate al valore assunto nel punto in esame.

Continuità uniforme

Una condizione più forte (e globale) di continuità è quella di continuità uniforme: una funzione continua tra due spazi metrici si dice uniformemente continua se il parametro $\delta$ della definizione non dipende dal punto $p$ considerato, ovvero se è possibile scegliere un $\delta$ che soddisfi la definizione per tutti i punti del dominio.

Più precisamente, una funzione $f$ è uniformemente continua se, per ogni $\varepsilon >0$ esiste un $\delta >0$ tale che, comunque presi due punti $p$ e $q$ nel dominio di $f$ che distano per meno di $\delta$, allora le loro immagini $f(p)$ e $f(q)$ distano per meno di $\varepsilon$.

Equicontinuità

Quando gli elementi di un insieme di funzioni continue hanno il medesimo modulo di continuità, si parla di insieme equicontinuo. Nello specifico, Siano $X$ e $Y$ due spazi metrici e $F$ una famiglia di funzioni definite da $X$ in $Y$. La famiglia $F$ è equicontinua nel punto $x_{0}\in X$ se per ogni $\epsilon >0$ esiste $\delta >0$ tale che $d(f(x_{0}),f(x))<\epsilon$ per tutte le $f\in F$ e per ogni $x$ tali che $d(x_{0},x)<\delta$. La famiglia $F$ è equicontinua (in tutto $X$) se è equicontinua in ogni suo punto. La famiglia $F$ è uniformemente equicontinua se per ogni $\epsilon >0$ esiste $\delta >0$ tale che $d(f(x_{1}),f(x_{2}))<\epsilon$ per tutte le $f\in F$ e per ogni coppia di punti $x_{1}$ e $x_{2}$ in $X$ tali che $d(x_{1},x_{2})<\delta$.

Più in generale, quando $X$ è uno spazio topologico, un insieme $F$ di funzioni da $X$ in $Y$ è equicontinuo nel punto $x\in X$ se per ogni $\epsilon >0$ il punto $x$ possiede un intorno $U_{x}$ tale che:

$d_{Y}(f(y),f(x))<\epsilon \qquad \forall y\in U_{x},\quad \forall f\in F.$

Tale definizione è sapesso utilizzata nell'ambito degli spazi vettoriali topologici.

Spazio delle funzioni continue

L'insieme di tutte le funzioni continue su un dominio fissato $A$ e a valori reali:

$C(A,\mathbb {R} ):=\{f:A\to \mathbb {R} {\text{ }}|{\text{ }}f{\text{ è continua}}\}$

può essere dotato di una struttura di spazio vettoriale ponendo per $f$ e $g$ in tale insieme:

${\begin{matrix}f+g:&A&\longrightarrow &\mathbb {R} \\&x&\longmapsto &f(x)+g(x)\end{matrix}}$

e per $\alpha$ numero reale:

${\begin{matrix}\alpha f:&A&\longrightarrow &\mathbb {R} \\&x&\longmapsto &\alpha f(x)\end{matrix}}$

Lo spazio vettoriale così definito è detto spazio delle funzioni continue su $A$.

Se il dominio $A$ è compatto (e quindi per tutte le funzioni in $C(A,\mathbb {R} )$ vale il teorema di Weierstrass) nello spazio $C(A,\mathbb {R} )$ può essere definita una norma ponendo:

$\left\|f\right\|_{\infty }:=\sup _{x\in A}f(x)$

detta norma uniforme o norma del sup.

La coppia costituita dallo spazio $C(A,\mathbb {R} )$ e dalla norma uniforme individua uno spazio di Banach.

Bibliografia

• (EN) Michael Reed, Barry Simon, Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis, 2ª ed., San Diego, California, Academic press inc., 1980, ISBN 0-12-585050-6.
• Paolo Marcellini, Carlo Sbordone, Analisi Matematica Uno, Liguori Editore, 1998, ISBN 9788820728199.
• Paolo Maurizio Soardi, Analisi Matematica, CittàStudi, 2007, ISBN 978-88-251-7319-2.
• Marco Manetti, Topologia, Springer, 2008, ISBN 978-88-470-0756-7.
• (EN) Tom M. Apostol, Calculus, vol. 1, John Wiley & Sons, inc., 1967, ISBN 0-471-00005-1.
• (EN) A.V. Arkhangel'skii, Pontryagin, L.S., General Topology I, Springer-Verlag, 1990, ISBN 3-540-18178-4.
• Nicola Fusco, Paolo Marcellini, Carlo Sbordone: Lezioni di Analisi Matematica Due, Zanichelli, 2020, ISBN 9788808520203.
• Enrico Giusti, Analisi matematica 2, Bollati Boringhieri, 2008, ISBN 978-88-339-5706-7.

Voci correlate

• Classe C di una funzione
• Continuità assoluta
• Continuità uniforme
• Continuità separata
• Funzione semicontinua
• Modulo di continuità
• Operatore lineare continuo
• Punto di accumulazione
• Punto di discontinuità
• Funzione derivabile

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su funzione continua

Collegamenti esterni

• (EN) continuous function, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Funzione continua / Funzione continua (altra versione), su MathWorld, Wolfram Research.
• (EN) Funzione continua, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.