Derivata parziale
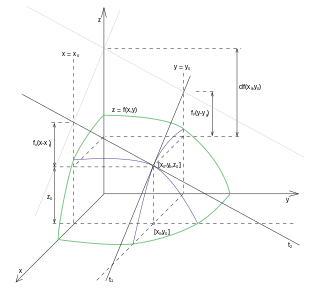
In analisi matematica, la derivata parziale è una prima generalizzazione del concetto di derivata di una funzione reale alle funzioni di più variabili. Se per funzioni reali la derivata in un punto rappresenta la pendenza del grafico della funzione (una curva contenuta nel piano ), la derivata parziale in un punto rispetto (ad esempio) alla prima variabile di una funzione rappresenta la pendenza della retta tangente alla curva ottenuta intersecando il grafico di (una superficie contenuta nello spazio ) con un piano passante per il punto e parallelo al piano .
Come tecnica di calcolo, la derivata parziale di una funzione rispetto a una variabile (lo stesso discorso può ripetersi per le altre variabili , ecc.) in un punto si ottiene derivando la funzione nella sola variabile , considerando tutte le altre variabili come se fossero costanti.
Definizione[modifica | modifica wikitesto]
Sia una funzione definita su un insieme aperto dello spazio euclideo
Dette e le basi canoniche di e rispettivamente, la funzione può essere scritta nel seguente modo:
La componente -esima della funzione è allora:
Si definisce derivata parziale di rispetto alla variabile il limite:[1]
Tale limite è a volte chiamato limite del rapporto incrementale di nel punto , e viene denotato anche con . La derivata parziale di una funzione, o nel caso di funzione vettoriale di una sua componente, si effettua quindi considerando le variabili diverse da quella rispetto a cui si vuole derivare come costanti e calcolandone il rapporto incrementale.
Se una funzione è differenziabile in , allora tutte le derivate parziali esistono in ,[1] e determinano completamente l'applicazione lineare che permette di approssimare la funzione nel punto:[2]
dove si annulla all'annullarsi dell'incremento .
La trasformazione è rappresentata nella base canonica dalla matrice jacobiana, ed è chiamata derivata della funzione in .
Il calcolo delle derivate parziali può essere svolto tramite il calcolo di derivate ordinarie. Supponendo di voler calcolare , si definisce . Allora:
La derivata parziale di in rispetto a è la derivata che si ottiene considerando la funzione come funzione della sola e considerando costanti le rimanenti.
Derivate parziali in R2[modifica | modifica wikitesto]
Si consideri una funzione con dominio in , insieme formato da tutte le coppie ordinate con e con valori in Tale funzione in ogni punto del proprio dominio può essere derivata sia rispetto a :
sia rispetto a :
Se entrambi i limiti esistono finiti, allora la funzione si dice derivabile in . Il vettore che ha per componenti e è detto gradiente della funzione in e si indica
Derivata direzionale[modifica | modifica wikitesto]
La derivata parziale è un caso particolare di derivata direzionale. Usando questo concetto si può definire la derivata parziale come:
con , ovvero il versore -esimo, cioè quel vettore, di modulo unitario, che ha tutte le componenti nulle tranne la -esima che è uguale a .
Notazioni[modifica | modifica wikitesto]
La notazione più comune fa uso del simbolo [3] simile alla usata nella notazione di Leibniz per la derivata di funzioni di una variabile. Altre notazioni per indicare la derivata di rispetto alla prima variabile () sono:
dove l'ultima notazione fa uso dei cosiddetti multiindici.
Derivate parziali di ordine superiore[modifica | modifica wikitesto]
Le operazioni di derivazione possono essere applicate anche alle funzioni ottenute come derivate parziali di una data funzione. Si possono definire quindi derivate parziali di ordine superiore al primo.
Si distingue a questo punto tra derivate parziali pure, quelle ottenute derivando ripetutamente sempre rispetto alla stessa variabile, e derivate parziali miste, cioè quelle in cui le variabili di derivazione non sono sempre le stesse. Un importante risultato, noto come teorema di Schwarz, afferma che se le derivate miste di second'ordine sono continue allora l'ordine di derivazione è ininfluente (cioè derivare prima rispetto e poi rispetto porta allo stesso risultato di derivare prima rispetto a e poi rispetto ).
Continuità delle derivate parziali[modifica | modifica wikitesto]
Se una funzione ha le derivate parziali prime continue nel suo dominio in , si dice che è una funzione di classe (si legge funzione di classe C uno in ).
In generale per un qualsiasi intero positivo se tutte le derivate parziali di ordine minore o uguale a della funzione sono continue nell'insieme di definizione , si dice che è di classe
Un punto di una superficie di equazione , si dice punto semplice se le tre derivate parziali della funzione sono continue e non nulle. Se invece le derivate rispetto alle tre variabili sono nulle, oppure una non esiste, il punto si dice singolare.
Note[modifica | modifica wikitesto]
Bibliografia[modifica | modifica wikitesto]
- Nicola Fusco, Paolo Marcellini, Carlo Sbordone, Lezioni di Analisi Matematica Due, Zanichelli, 2020, ISBN 9788808520203, capitolo 3.
- Walter Rudin, Principi di analisi matematica, Milano, McGraw-Hill, 1991, ISBN 88-386-0647-1.
Voci correlate[modifica | modifica wikitesto]
- Continuità separata
- Derivata direzionale
- Derivata totale
- Differenziale (matematica)
- Divergenza
- Equazione di Poisson
- Gradiente
- Laplaciano
- Nabla
- Rotore (fisica)
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) partial derivative, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Derivata parziale, su MathWorld, Wolfram Research.
| Controllo di autorità | GND (DE) 4454857-6 |
|---|





























































