Integrale multiplo


L'integrale multiplo è una forma di integrale definito esteso a funzioni di più variabili reali (ad esempio a funzioni della forma o della forma ).
Gli integrali definiti possiedono interpretazioni geometriche e fisiche significative: limitandosi per semplicità alle funzioni con valori positivi, mentre l'integrale definito per una funzione di una variabile rappresenta l'area della regione chiamata trapezoide compresa tra il suo grafico e l'asse delle ascisse, l'integrale definito per funzioni di due variabili (integrale doppio) fornisce la misura del volume del solido chiamato cilindroide compreso tra la superficie che ne dà il grafico e il piano contenente il suo dominio.
In generale gli integrali definiti di funzioni di 3 o più variabili sono interpretabili come misure di ipervolumi, ovvero di volumi di solidi di 4 o più dimensioni, non rappresentabili quindi graficamente. Un integrale triplo, integrale definito di una funzione di tre variabili, è interpretabile fisicamente come misura della massa di un corpo che occupa lo spazio che corrisponde al dominio e che ha la densità variabile fornita dai valori della funzione stessa.
Definizione[modifica | modifica wikitesto]
La definizione di integrale di Riemann nel caso di funzioni di più variabili è concettualmente simile a quella di integrale in una sola variabile, ma è complessivamente più laboriosa a causa della varietà di insiemi su cui è eseguita l'integrazione. Le funzioni semplici con cui approssimare le funzioni sono infatti definite su un'unione finita di rettangoli nella forma:[1]
dove . La misura di Peano-Jordan di ogni rettangolo è:
e una funzione semplice è definita da:
dove i coefficienti sono costanti reali, è una successione di rettangoli in e è la funzione caratteristica di . Se i rettangoli sono tutti disgiunti, e detta la loro unione, si definisce l'integrale della funzione semplice su nel seguente modo:
In questo contesto, una funzione è detta integrabile se può essere approssimata con precisione arbitraria da funzioni semplici maggioranti e minoranti. In modo equivalente, se per ogni esistono due funzioni semplici e tali che e:
Se è integrabile, il suo integrale è il limite degli integrali di e al crescere del numero di rettangoli, ossia al tendere a del loro diametro. Equivalentemente: l'integrale è l'estremo superiore degli integrali delle funzioni semplici minoranti, che è uguale all'estremo inferiore degli integrali delle funzioni semplici maggioranti.

Non è necessario che l'insieme dove operare l'integrale sia un'unione finita di rettangoli: poiché l'unione è limitata, è sempre possibile estendere la funzione integranda su un rettangolo "ambiente" contenente il dominio della funzione di partenza, considerando la funzione
Si definisce l'integrale di su come l'integrale di su . Tale definizione è ben posta in quanto si verifica facilmente che l'integrabilità e il valore dell'integrale non dipendono dalla scelta di , purché contenga .
Nel caso dell'integrale di Lebesgue, invece, la definizione non varia in nessun modo all'aumentare da una a più dimensioni, in quanto si basa solamente sulla misura degli insiemi. Anche in questo caso, per definire una misura su , si parte dai rettangoli e dalle loro unioni finite: queste formano un'algebra, su cui la misura definita precedentemente è σ-additiva. Allora, per il teorema di Carathéodory, questa può essere estesa a una misura (detta misura di Lebesgue) sulla σ-algebra di Lebesgue.
Proprietà[modifica | modifica wikitesto]
L'integrale multiplo condivide le proprietà che caratterizzano l'integrale per funzioni ad una variabile: è lineare, additivo (ovvero è possibile spezzare il dominio d'integrazione), monotono; il valore assoluto dell'integrale verifica
Valgono inoltre il teorema della media integrale e il teorema della media pesata.
Integrali doppio e triplo[modifica | modifica wikitesto]
Dalla definizione generale, nel caso in cui sia un sottoinsieme del piano, a volte si pone
e si parla di integrale doppio su ; allo stesso modo, se è un sottoinsieme di , il suo integrale triplo è
Nelle applicazioni più tecniche, come quelle nel campo dell'ingegneria, la tipologia dei problemi analizzata comporta quasi esclusivamente integrali doppi e tripli.
Integrale improprio[modifica | modifica wikitesto]

Come nel caso di una sola variabile, la definizione di integrale di Riemann richiede di integrare funzioni limitate su insiemi limitati. Per estendere la definizione agli altri casi, il primo passo è prendere in esame le funzioni positive, e considerare una successione crescente di compatti (ovvero di chiusi limitati in cui ) dove la funzione è limitata, il cui limite (che coincide con la loro unione) sia l'insieme di integrazione . In tal caso, la successione degli integrali sugli è una successione crescente, e quindi ha un limite; data inoltre un'altra successione di insiemi con le stesse caratteristiche, ogni elemento di quest'ultima è compreso tra due elementi (non necessariamente consecutivi) della prima, e quindi per il teorema dei carabinieri il limite è lo stesso.
Nel caso di funzioni a segno qualsiasi, è sufficiente dividerla nella sua parte positiva e nella sua parte negativa; l'integrale sarà quindi definito nel caso in cui possa essere definito separatamente per entrambe. Questo è equivalente a chiedere che l'integrale (improprio) del suo valore assoluto sia finito.[2]
L'integrale di Lebesgue, invece, non ha bisogno di questa costruzione, in quanto la sua definizione comprende già i casi in cui la funzione o il dominio d'integrazione non sono limitati.
Metodi di integrazione[modifica | modifica wikitesto]
La risoluzione dei problemi con integrali multipli consiste nella maggior parte dei casi nel riuscire a ricondurre i calcoli a una serie di integrali a una variabile, gli unici direttamente risolvibili.
Esame diretto[modifica | modifica wikitesto]
In pochi casi particolari è possibile evitare calcoli diretti e ottenere subito il risultato dell'integrazione. Uno di questi è il caso di integrazioni di funzioni costanti su rettangoli: in tal caso, conoscendo la misura del dominio, basta moltiplicarla per il valore della costante . Se , in si avrà il volume di un parallelepipedo, mentre in il suo ipervolume.
In altri casi si può sfruttare la disparità della funzione rispetto ad una variabile in congiunzione con la simmetria del dominio rispetto all'asse corrispondente, ottenendo un integrale nullo: ad esempio, la funzione è dispari in , e quindi il suo integrale nel semicerchio superiore è uguale a .
Formule di riduzione[modifica | modifica wikitesto]
Un elemento essenziale nel calcolo degli integrali multipli è dato dalla possibilità di "spezzare" l'integrale in più dimensioni in diversi integrali su , dove può essere applicato, ad esempio, il teorema fondamentale del calcolo integrale. Si vorrebbe avere cioè una formula del tipo
dove, per semplicità di notazione, si considerano gli integrali sull'intero spazio (cui ci si può sempre ricondurre moltiplicando per la funzione caratteristica): in questo caso, si può risolvere prima l'integrale più a destra (trattando le prime variabili come costanti) e poi la parte restante, eventualmente portando fuori un'altra variabile (e così via). Questa formula tuttavia non è sempre valida. Nel caso più generale, i due teoremi fondamentali in questo caso sono il teorema di Tonelli e quello di Fubini: il primo garantisce la validità della formula nel caso di funzioni positive, mentre il secondo nel caso di funzioni il cui integrale del valore assoluto converge. Sono in un certo senso analoghi, rispettivamente, ai teoremi della convergenza monotona e della convergenza dominata per lo scambio delle operazioni di limite e integrale. Un altro caso in cui si può effettuare la riduzione, più particolare ma di considerevole interesse pratico, è nel caso che sia continua e l'insieme di integrazione sia un rettangolo limitato.
Entrambi si riferiscono ad espressioni più generali di quella precedente: l'integrale può essere infatti diviso in due parti di qualunque dimensione (purché, ovviamente, la loro somma sia uguale alla dimensione di partenza). Sebbene la maggior parte degli integrali non abbia bisogno di questa generalizzazione, essa è utile, ad esempio, per il calcolo del volume delle ipersfere, cioè delle sfere -dimensionali.[3]

L'estensione dell'integrale a tutto , sebbene utile nella dimostrazione dei teoremi di Tonelli e Fubini, non è tuttavia agevole per il calcolo effettivo degli integrali. In questo caso si sfrutta la nozione di dominio semplice (detto anche normale): questo è un insieme in cui una coordinata è costantemente compresa tra i valori di due funzioni (misurabili) delle altre variabili. Ad esempio, nel caso di due variabili, l'integrale di su un dominio normale rispetto all'asse , definito dalle funzioni e , con tra e , è
mentre, se il dominio fosse normale rispetto all'asse , si avrebbe
Cambio di variabili[modifica | modifica wikitesto]
A volte il dominio su cui bisogna integrare non è facilmente rappresentabile in forma normale (ad esempio perché dato in forma implicita). In questo caso si può ricorrere ad un cambio di variabili per aggirare il problema e integrare funzioni note su regioni "comode", ovvero domini semplici o comunque descrivibili in maniera più semplice. Formalmente, dati due insiemi e , una funzione e un diffeomorfismo (cioè un'applicazione biunivoca, differenziabile e con inversa differenziabile) da ad , allora:[4]
dove indica la matrice jacobiana di . In pratica, le variabili vengono trasformate secondo il cambio di variabile, ma compare un "elemento di volume" corrispondente al determinante della jacobiana.
Ad esempio, volendo integrare la funzione sull'insieme , una possibile trasformazione è
cioè
la cui jacobiana è
e il cui determinante è quindi
che è possibile risolvere usando il teorema di Tonelli (o quello di Fubini).
Alcuni cambi di variabile sono molto comuni: il primo, in due dimensioni, è il passaggio a coordinate polari, mentre gli altri due, in , sono il passaggio a coordinate cilindriche e a coordinate sferiche.
Coordinate polari e sferiche[modifica | modifica wikitesto]

In , se il dominio sul quale si deve integrare presenta una simmetria radiale o delle caratteristiche circolari, un cambio di variabile molto usato è il passaggio in coordinate polari. La relazione fondamentale per effettuare la trasformazione della funzione è
L'elemento d'area della trasformazione è
La formula totale del passaggio in coordinate polari è quindi
L'intervallo massimo in cui può variare è , mentre , essendo la misura di una lunghezza, può avere esclusivamente valori positivi.
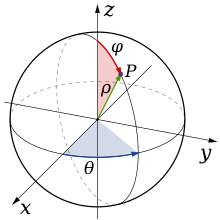
In più di due dimensioni, le coordinate polari sono generalizzate dalle coordinate sferiche e da quelle ipersferiche (per quattro o più dimensioni; sono dette anche "sferiche generalizzate" o semplicemente "sferiche"). In tre dimensioni una possibile trasformazione è
dove varia tra e , mentre tra e ; , come nel caso precedente, può andare da a infinito. Lo jacobiano della trasformazione è:
Il dominio di integrazione che meglio si adatta a questo passaggio è ovviamente la sfera.
In dimensioni, il passaggio di coordinate impiega, oltre alla distanza , anche angoli , l'ultimo dei quali assume valori che variano tra e , mentre gli altri tra e :
cui corrisponde un elemento di volume
Coordinate cilindriche[modifica | modifica wikitesto]

Un'altra possibile generalizzazione delle coordinate polari ad sono le coordinate cilindriche. In esse, un piano (tipicamente quello ) è parametrizzato attraverso le coordinate polari, mentre l'altezza rimane invariata: questo cambio di variabili è quindi adatto per domini con una base circolare o, comunque, in cui la difficoltà d'integrazione è slegata da una delle variabili (ad esempio se l'insieme di integrazione è un cilindro o un cono).
La relazione è
e, poiché l'ultima variabile rimane fissa ed è totalmente indipendente dalla variazione delle altre, l'elemento d'area coincide con quello del passaggio in coordinate polari, cioè è esattamente .
Per completezza lo si dimostra:
Esempio di applicazioni matematiche[modifica | modifica wikitesto]
Calcoli di volume[modifica | modifica wikitesto]
Grazie ai metodi precedentemente descritti è possibile dimostrare il valore del volume di alcuni solidi.
- Cilindro
- Considerando come dominio la base circolare di raggio e come funzione la costante dell'altezza , si applica direttamente il passaggio in coordinate polari.
- Verifica: Volume = area di base * altezza =
- Sfera
- È di rapida dimostrazione la formula applicando il passaggio in coordinate sferiche della funzione costante integrato sulla sfera di raggio stessa.
- Il volume del tetraedro con vertice nell'origine e spigoli di lunghezza adagiati sui tre assi cartesiani può essere calcolato tramite le formule di riduzione considerando, ad esempio, la normalità rispetto al piano e all'asse e come funzione la costante .
- Verifica: Volume = area di base * altezza / 3 =
Integrali in una dimensione[modifica | modifica wikitesto]
A volte un integrale multiplo può semplificare il calcolo di un integrale in una sola variabile. Un esempio classico è il calcolo della funzione gaussiana, fondamentale nella teoria della probabilità, esteso a tutto l'intervallo reale. L'integrale da calcolare è
Il suo quadrato si può scrivere come
ove si è usato il teorema di Tonelli. Passando in coordinate polari si ottiene
che può essere integrato facilmente ottenendo
e quindi
Attraverso questa tecnica è possibile calcolare (riconducendo l'integrale a quello appena calcolato) il valore della funzione gamma in : esso è
che, attraverso la trasformazione , risulta essere uguale a
Sommatorie[modifica | modifica wikitesto]
Un interessante esempio di utilizzo dell'integrale multiplo è nel calcolo dei valori della funzione zeta di Riemann. Infatti può essere riscritto come
sfruttando il teorema della convergenza monotona per scambiare la serie e l'integrale. Effettuando la sostituzione
si ha
dove è il determinante jacobiano e il dominio è il quadrato che ha per diagonale il segmento di estremi e ; questo è simmetrico rispetto all'asse , così come la funzione e quindi l'integrale può essere calcolato solo su metà del dominio, e poi spezzato come
e notando che in entrambi i casi la derivata dell'arcotangente è l'altro fattore (a parte per una costante nel secondo caso), si ottiene
In maniera simile, usando un integrale -dimensionale, si possono calcolare i valori di .[5]
Volume di un solido di rotazione[modifica | modifica wikitesto]
Nel caso del calcolo del volume di un solido di rotazione è possibile sfruttare una formulazione alternativa semplificata che deriva da un cambiamento di coordinate sferico. Nel caso di un solido che ruota attorno all'asse e poggia sul piano abbiamo:
dove e sono gli estremi in cui è compreso e è una funzione che descrive il comportamento del raggio del solido di rotazione sul piano . La formulazione, alternativa al teorema di Pappo-Guldino, si può estendere anche al caso di una rotazione sugli altri assi.
Alcune applicazioni pratiche[modifica | modifica wikitesto]

Questi integrali sono utilizzati in numerosi ambiti della fisica.
In meccanica il momento d'inerzia viene calcolato come un integrale di volume (ovvero un integrale triplo) della densità pesata col quadrato della distanza dall'asse:
Nell'ambito dell'elettromagnetismo le equazioni di Maxwell possono essere scritte sotto forma di integrali multipli per calcolare i campi elettrici e magnetici totali. Ad esempio il campo elettrico generato da una distribuzione di carica si ottiene tramite un integrale triplo di una funzione vettoriale:
Note[modifica | modifica wikitesto]
- ^ Per evitare sovrapposizioni tra due rettangoli, gli intervalli sono considerati chiusi a sinistra e aperti a destra. Si potrebbe procedere allo stesso modo con intervalli aperti a sinistra e chiusi a destra.
- ^ Giusti, pp. 64–66.
- ^ Giusti, pp. 46–48.
- ^ W. Rudin, p. 256.
- ^ Martin Aigner, Günter M. Ziegler, Proofs from THE BOOK, Milano, Springer, 2006, ISBN 88-470-0435-7.
Bibliografia[modifica | modifica wikitesto]
- Walter Rudin, Principi di analisi matematica, Milano, McGraw-Hill, 1991, ISBN 88-386-0647-1.
- Robert A. Adams, Calcolo differenziale 2. Funzioni di più variabili, Milano, CEA, 2007, ISBN 88-408-1390-X.
- Enrico Giusti, Analisi matematica 2, Torino, Bollati Boringhieri, 2003, ISBN 88-339-5706-3.
- (EN) Richard L. Wheeden e Antoni Zygmund, Measure and Integral - An introduction to Real Analysis, CRC Press, 1977, ISBN 0-8247-6499-4.
- Nicola Fusco, Paolo Marcellini, Carlo Sbordone, Lezioni di Analisi Matematica Due, Zanichelli, 2020, ISBN 9788808520203, capitoli 8 e 9.
Voci correlate[modifica | modifica wikitesto]
- Integrale
- Teorema della divergenza
- Teorema del rotore
- Teorema di Green
- Teorema di Stokes
- Teorema di Fubini
Collegamenti esterni[modifica | modifica wikitesto]
- integrale multiplo, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) multiple integral, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Integrale multiplo, su MathWorld, Wolfram Research.
- (EN) Integrale multiplo, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
| Controllo di autorità | Thesaurus BNCF 19573 · GND (DE) 4224692-1 · BNE (ES) XX552555 (data) |
|---|































































































![{\displaystyle {\begin{aligned}{\text{Volume}}&=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{R}h\rho \;\mathrm {d} \rho \\&=h2\pi \left[{\frac {\rho ^{2}}{2}}\right]_{0}^{R}\\&=\pi R^{2}h\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea6205ce745ca5d18bf155ae9c4ac7d8f70b8a41)


![{\displaystyle {\begin{aligned}{\text{Volume}}&=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }\sin \theta \;\mathrm {d} \theta \int _{0}^{R}\rho ^{2}\;\mathrm {d} \rho \\&=2\pi \int _{0}^{\pi }\sin \theta {\frac {R^{3}}{3}}\;\mathrm {d} \theta \\&={\frac {2}{3}}\pi R^{3}{\Big [}-\cos \theta {\Big ]}_{0}^{\pi }\\&={\frac {4}{3}}\pi R^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/440ca3d00df781982b71b3bdb3d35597de26ee48)


![{\displaystyle {\begin{aligned}{\text{Volume}}&=\int _{0}^{l}\;\mathrm {d} x\int _{0}^{l-x}\;\mathrm {d} y\int _{0}^{l-x-y}\;\mathrm {d} z\\&=\int _{0}^{l}\;\mathrm {d} x\int _{0}^{l-x}(l-x-y)\;\mathrm {d} y\\&=\int _{0}^{l}\left(l^{2}-2lx+x^{2}-{\frac {(l-x)^{2}}{2}}\right)\;\mathrm {d} x\\&=l^{3}-ll^{2}+{\frac {l^{3}}{3}}-\left[{\frac {l^{2}}{2}}-lx+{\frac {x^{2}}{2}}\right]_{0}^{l}\\&={\frac {l^{3}}{3}}-{\frac {l^{3}}{6}}\\&={\frac {l^{3}}{6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f743d7f0817591c65c55f1db009f965813489ea8)




![{\displaystyle I^{2}=-\int _{0}^{2\pi }\mathrm {d} \theta \left[e^{-{\frac {\rho ^{2}}{2}}}\right]_{\rho =0}^{\rho =+\infty }=\int _{0}^{2\pi }\mathrm {d} \theta =2\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a5c3d97d33b3dedace9919a229a331e9152fc7)







![{\displaystyle =\sum _{n=0}^{+\infty }\left(\int _{[0,1]^{2}}x^{n}y^{n}\mathrm {d} x\mathrm {d} y\right)=\int _{[0,1]^{2}}\sum _{n=0}^{+\infty }x^{n}y^{n}\mathrm {d} x\mathrm {d} y=\int _{[0,1]^{2}}{\frac {1}{1-xy}}\mathrm {d} x\mathrm {d} y,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d0de18906368db7e5bfd204d17664dc07cdb8c)


![{\displaystyle \int _{[0,1]^{2}}{\frac {1}{1-xy}}\mathrm {d} x\mathrm {d} y=\int _{A}{\frac {2}{1-u^{2}+v^{2}}}\mathrm {d} u\mathrm {d} v,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7d59d24d16d92c766857d7a5c873b6dff17c80)


















