Campo elettrico

Da Wikipedia, l'enciclopedia libera.

Questa voce o sezione di fisica non riporta fonti o riferimenti sufficienti.

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili, secondo le linee guida sull'uso delle fonti.

Il campo elettrico è una perturbazione dello spazio, conseguente alla presenza di cariche elettriche, che si propaga a velocità finita, ossia la velocità della luce.

Indice

1 Introduzione
2 Campo elettrostatico nel vuoto
3 Linee di flusso e superfici equipotenziali
4 Equazioni di Maxwell per il campo elettrostatico
5 Condizioni di raccordo tra dielettrici
6 Campo creato da una carica in moto
7 Voci correlate

[modifica] Introduzione

Dati i fatti sperimentali come l'attrazione e la repulsione tra sostanze trattate in maniera opportuna (per esempio per strofinìo), si sono definiti due stati di elettrizzazione della materia: positiva e negativa. Corpi elettrizzati entrambi positivamente o entrambi negativamente si respingono mentre corpi elettrizzati in modo opposto si attraggono. Per riconoscere l'elettrizzazione di un corpo si usa uno strumento chiamato elettroscopio a foglie, costituito da un'ampolla di vetro nella quale è inserita un'asta metallica la quale, all'interno dell'ampolla, ha due linguette metalliche molto sottili, mentre all'esterno essa può essere messa a contatto con un corpo carico. Mettendo a contatto un corpo carico ad esempio positivamente con l'asta, si nota facilmente come le linguette (giustappunto chiamate foglie) si allontanano l'una dall'altra, in proporzione all'elettrizzazione del corpo che è stato messo a contatto e in opposizione al loro peso che tende a farle ricadere verso il basso. Questo dimostra soprattutto come l'elettrizzazione del corpo si "trasferisca" alle foglie dell'elettroscopio. Si parla di quantità di carica o di quantità di elettricità trasferita. Questa nuova grandezza fisica è una misura quantitativa dello stato di elettrizzazione della materia. Mettendo a contatto un corpo carico (cioè elettrizzato, in qualche modo) con un corpo non carico, quello che succede è semplicemente che una certa quantità di carica si trasferisce sean pike locke is awesome all'altro corpo.

Tutto ciò è dovuto alla natura microscopica della materia e in particolare alle proprietà dei componenti fondamentali dell'atomo. Infatti ogni atomo è composto dal nucleo ove risiedono protoni e neutroni e da una zona esterna dove si trovano gli elettroni. In condizioni normali un atomo è neutro, cioè ha lo stesso numero di elettroni e protoni. Per quantificare la carica elettrica si prende allora la carica più piccola esistente in natura, quella dell'elettrone che è negativa e pari a e = 1,602 189 2 ∙ 10^-19 C, uguale ed opposta a quella del protone, dove C è l'unità di misura della carica chiamata coulomb nel SI. Il neutrone non possiede carica elettrica. Così un corpo carico elettricamente di una certa carica Q, ha in effetti una carica data da un numero intero di volte la carica elementare, se negativa: -Q = n ∙ e; vale inoltre il principio di conservazione della carica elettrica, secondo il quale in un sistema isolato, la somma algebrica delle cariche elettriche è costante.

Importante far notare che la presenza di carica negativa in un corpo è dovuta all'eccesso di elettroni che si trasferiscono a questo corpo, viceversa, la presenza di carica positiva è dovuta a difetto di elettroni e non al trasferimento di protoni. Questo è anche il motivo per cui l'asta dell'elettroscopio è isolata dall'ampolla di vetro, altrimenti gli elettroni si trasferirebbero anche sul vetro, producendo un effetto minimo se non nullo sulle foglie.

Infine, la differenza fondamentale tra conduttori e isolanti: i primi sono in genere metalli che per la loro struttura reticolare hanno elettroni esterni debolmente legati ai rispettivi nuclei, essi possono facilmente staccarsi e viaggiare entro il reticolo cristallino. Un tale tipo di legame è detto legame metallico, e la disponibilità di elettroni liberi rende tali materiali conduttori, poiché lo strofinìo produce l'energia necessaria a far passare una certa quantità di elettroni da un corpo ad un altro. I secondi invece, sono generalmente non metalli o composti, che hanno elettroni fortemente legati ai nuclei, per questo motivo non vi sono all'interno dell'isolante che pochi elettroni liberi, che ne fanno pessimi conduttori; un discorso a parte va fatto per alcuni elementi che hanno proprietà intermedie tra questi, i cosiddetti semiconduttori, che proprio per le loro particolari caratteristiche vengono utilizzati in elettronica. A partire da questi fatti sperimentali Coulomb formulò la sua famosa Legge di Coulomb, quantificando la forza elettrica attrattiva o repulsiva che due corpi puntiformi carichi elettricamente si scambiano a distanza. Questa legge fondamentale è il punto di partenza di tutta la teoria dell'elettricità e dell'elettrostatica, che permette di introdurre i concetti di campo elettrico.

Un corpo carico elettricamente produce nello spazio circostante (al limite in tutto lo spazio circostante), la presenza di un nuovo stato di cose: se introduciamo un'altra carica elettrica, questa risente l'effetto di una forza , appunto la forza elettrica o forza di Coulomb, che segue la legge di Coulomb, cioè essa è direttamente proporzionale al prodotto delle due cariche e inversamente proporzionale al quadrato della loro distanza. Questo nuovo stato di cose è quello che chiamiamo campo elettrico, che è un campo vettoriale di forze.

[modifica] Campo elettrostatico nel vuoto

Se nello spazio poniamo una carica elettrica Q possiamo determinare la forza che produce su una carica molto piccola e per convenzione positiva posta nelle vicinanze detta carica di prova q₀. Come si vede dall'esperienza, tale forza è proporzionale alla carica elettrica di prova q₀; è quindi logico definire il vettore campo elettrico E in un punto, come il rapporto tra la forza elettrica generata dalla carica Q e il valore della carica di prova stessa; questo rapporto rende indipendente il campo dalla particolare carica di prova usata:

$\mathbf E = \frac {\mathbf F} {q_0}$

(Dalla definizione si ricava che l'unità di misura del campo elettrico è $\frac{N}{C}$ , cioè newton/coulomb. Essa equivale anche a $\frac{V}{m}$ , cioè volt/metro).

In realtà, per una maggiore precisione matematica, bisognerebbe dire che il rapporto precedente viene calcolato con delle cariche di prova q_{0 i}, positive e via via sempre più piccole senza mai essere nulle, cioè il campo elettrico è definito tramite il limite

$\mathbf{E}=\lim_{q_{0} \to 0}\frac{\mathbf{F}}{q}$ ,

ciò perché la carica di prova non deve perturbare il campo elettrico dovuto alla carica detta generatrice, Q.

Campo elettrostatico per una carica puntiforme nello spazio

In questo modo, dalla legge di Coulomb, come nella figura sopra, per una carica puntiforme Q posta in r' (ad esempio un monopolo elettrico), il campo elettrico, in un punto qualsiasi r, è definito dalla seguente espressione:

$\mathbf E (\mathbf r) = \frac {Q}{4 \pi \epsilon_0} \frac {\mathbf r - \mathbf r'}{\left \| \mathbf r - \mathbf r' \right \|^3}$

dove ε₀ è la costante dielettrica nel vuoto, assumendo di considerare successivamente il caso del campo elettrico nella materia.

Per un numero n di cariche puntiformi q_i distribuite nello spazio, possiamo calcolare il campo elettrostatico in un punto P, identificato dal vettore posizione r:

$\mathbf E_0(\mathbf r) = \displaystyle\sum_{i=1}^n \mathbf E_{0i} (\mathbf r) = \frac {1}{4 \pi \epsilon_0} \sum_{i=1}^n q_i \frac {\mathbf r - \mathbf r'} {\left \| \mathbf r - \mathbf r' \right \|^3}$

Per una distribuzione continua di carica, si può ancora scrivere:

$\mathbf E_0(\mathbf r) = \frac {1}{4 \pi \epsilon_0} \iiint_{\Omega} \rho(\mathbf r')\frac {\mathbf r - \mathbf r'} {\left \| \mathbf r - \mathbf r' \right \|^3} \operatorname{d}x \operatorname{d}y \operatorname{d}z$

dove ρ(r) rappresenta la densità di distribuzione di carica nello spazio, ovvero:

$\rho(\mathbf r) = \lim_{\Delta V \to 0}\frac{\Delta q}{\Delta V} = \frac{\operatorname{d}q}{\operatorname{d}V}$

e Ω rappresenta il dominio occupato dalla distribuzione.

[modifica] Linee di flusso e superfici equipotenziali

Linee di flusso uscenti per il campo elettrico prodotto da una carica positiva nello spazio

Linee di flusso entranti per il campo elettrico prodotto da una carica negativa nello spazio

Linee di flusso prodotte da due cariche uguali ed opposte di segno nello spazio-Dipolo elettrico

Linee di flusso prodotte da due cariche uguali e dello stesso segno nello spazio

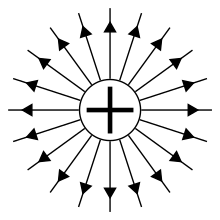
Il campo elettrico è un campo vettoriale rappresentato attraverso linee di campo (ortogonali in ogni punto dello spazio alle superfici equipotenziali), che sono più fitte intorno alla carica e si diradano all'aumentare della distanza. Se la carica considerata è positiva le linee di campo si dicono uscenti (si irradiano in tutte le direzioni a partire dalla carica) e la carica è definita sorgente; se la carica considerata è negativa le linee di campo sono dette entranti (sono dirette verso la carica) e la carica è definita pozzo.

Visto che il campo elettrico è il gradiente del potenziale

$\mathbf{E}_0 = - \operatorname{grad} V_0 = - \nabla V_0$

il potenziale è rappresentato attraverso un campo scalare caratterizzato da linee di livello a potenziale costante (dette per questo motivo superfici equipotenziali) perpendicolari alle linee di flusso del campo elettrico per definizione.

Nelle figure sono rappresentati esempi notevoli di linee di flusso da considerarsi nello spazio. Nelle prime due figure si hanno le linee di flusso di cariche isolate. Le successive invece sono rispettivamente le rappresentazioni delle linee di flusso di un dipolo elettrico cioè un sistema di due cariche uguali ed opposte e due cariche uguali che hanno linee di flusso che si respingono.

[modifica] Equazioni di Maxwell per il campo elettrostatico

Il campo si dice elettrostatico perché viene generato da una distribuzione di carica ρ(r) indipendente dal tempo. Inoltre il campo elettrostatico è conservativo, cioè la circuitazione del campo elettrostatico è nulla lungo qualsiasi linea chiusa:

$\oint_{\gamma} \mathbf E_0 \cdot \operatorname{d}\mathbf l = 0$

Questo segue dal fatto che una condizione necessaria e sufficiente perché un campo vettoriale sia conservativo in un insieme semplicemente connesso (ad esempio, un insieme stellato o convesso) è che l'integrale del campo lungo una linea chiusa sia nullo.

In maniera alternativa si può anche dire che il campo elettrostatico è conservativo, e quindi esiste una funzione scalare (il potenziale elettrico) tale che l'integrale per andare da un punto A ad un punto B non dipenda dal cammino percorso ma solo funzione degli estremi:

$\int_{A}^{B} \mathbf E_0 \cdot \operatorname{d}\mathbf l = -(V_0(B) - V_0(A))$

riuscendo: $\mathbf E_0 = - \nabla V_0$

[modifica] Nel vuoto

Ora possiamo dare le due equazioni fondamentali dell'elettrostatica nel vuoto che sono la prima e la terza equazione di Maxwell. Dal teorema della divergenza e dal teorema del flusso ricaviamo la prima equazione di Maxwell nel vuoto:

$(1)\qquad\nabla\cdot\mathbf E = \frac{\rho}{\epsilon_0}$ .

Per la conservatività del campo elettrostatico, ovvero utilizzando il rotore, possiamo dare la terza equazione di Maxwell nel vuoto nelle forme:

$(2)\qquad\mathbf E_0 = -\nabla V_0$

$(3)\qquad\nabla\times\mathbf E = 0$

Combinando la (1) con la (2) si ottiene:

$\operatorname{div}(\operatorname{grad} V_0) = \frac {\partial^2 V_0} {\partial x^2} + \frac {\partial^2 V_0} {\partial y^2} + \frac {\partial^2 V_0} {\partial z^2} = \nabla\cdot\nabla V_0 = \nabla^{2} V_0 = - \frac {\rho} {\epsilon_0}$

dove con $\nabla^{2}$ si indica l'operatore differenziale laplaciano; si ottiene la cosiddetta equazione di Poisson

$\nabla^{2} V = -\frac{\rho}{\epsilon_{0}}$ ,

che in condizioni di assenza di cariche diventa la nota equazione di Laplace

$\nabla^{2} V=0$ .

dalla quale risulta che in assenza di cariche il potenziale è una funzione armonica.

[modifica] Condizioni al contorno

Concretamente, risolvere l'equazione di Poisson in regioni di spazio limitate significa risolvere il problema generale dell'elettrostatica per opportune assegnate condizioni al contorno, con assenza o presenza di conduttori, presenza di cariche elettriche localizzate o no e così via. In particolare se ne distinguono tre tipi:

condizioni al contorno di Dirichlet

In questo caso il campo elettrostatico è generato da un sistema di conduttori di geometria nota e potenziali noti. Si risolve l'equazione di Laplace, dove le condizioni al contorno sono i potenziali V₀^∞ = 0 e V₀ = V_0i sui conduttori; una volta ricavati i potenziali per ogni punto nello spazio, si ricava il campo elettrostatico mediante:

$\mathbf E_0 = - \nabla V_0$

e poi determinare la densità di carica superficiali σ_i sui conduttori mediante il teorema di Coulomb. Infine si può trovare la carica netta totale su tutti i conduttori e i coefficienti di capacità su questi tramite il sistema:

$\begin{cases} Q_1 = c_{11} V_{01} + c_{12} V_{02} + \ldots + c_{1n} V_{0n} \\ Q_2 = c_{21} V_{01} + c_{22} V_{02} + \ldots + c_{2n} V_{0n} \\ \ldots \\ \ldots \\ Q_n = c_{n1} V_{01} + c_{n2} V_{02} + \ldots + c_{nn} V_{0n} \end{cases}$

condizioni al contorno di Neumann

In questo caso il campo elettrostatico è dato da un sistema di conduttori di geometria nota di cui sono note le cariche su ognuno di essi. In questo caso si danno dei potenziali arbitrari sui conduttori V₀ = V_0i^p e si risolve il problema di Dirichlet come sopra. Siccome le cariche sono note e i coefficienti di capacità sono indipendenti alle cariche e ai potenziali (dipendenti solo dal loro rapporto), dal sistema sopra si ricavano i veri V₀ = V_0i.

condizioni al contorno miste

Un esempio può essere quello di avere una distribuzione di carica ρ nota nello spazio e un sistema di conduttori di cui si conoscono solo le cariche su ognuno di essi. Il problema è risolvere l'equazione di Poisson.

[modifica] In presenza di dielettrici

Finora si è parlato di campo elettrostatico nel vuoto attraverso la costante dielettrica nel vuoto ε₀. Nel caso ci si trovi in presenza di mezzi materiali si ha un effetto di polarizzazione della materia. Questo fenomeno è sperimentalmente accertato come un effetto capace di diminuire il potenziale elettrico in un condensatore e all'opposto aumentare la sua capacità elettrica, di uno stesso fattore che si chiama costante dielettrica relativa ε_r.

La presenza di materiale nello spazio ove esista un campo elettrico E modifica il campo stesso perché si polarizza e si crea entro il materiale una certa quantità di carica indotta che va sotto il nome di carica di polarizzazione ρ_p, rappresentata dal vettore polarizzazione elettrica P. Partendo dalle equazioni di Maxwell per il campo elettrostatico nel vuoto dove però la prima equazione va modificata aggiungendo le cariche di polarizzazione:

$\nabla \cdot \mathbf E = \frac {\rho + \rho_p}{\epsilon_0}$

Poiché la densità di carica di polarizzazione ρ_p = - ∇ ∙ P, possiamo, con semplici passaggi matematici, porre sotto la divergenza:

$\nabla \cdot (\epsilon_0 \mathbf E + \mathbf P) = \rho$

e così eliminare dall'equazione le cariche di polarizzazione che sono in generale ignote. Si chiama D = ε₀ E+ P vettore spostamento elettrico ed è necessario chiarire quale sia la relazione che intercorre tra D e E, ovvero tra P e E (vedi Polarizzazione nei materiali). Se questa relazione si riduce ad un fattore costante, il materiale si dice dielettrico omogeneo e isotropo, caso più semplice in cui la relazione diventa:

$\mathbf D = \epsilon_0 \epsilon_r \mathbf E = \epsilon \mathbf E$

dove ε è la costante dielettrica assoluta del materiale. In questo caso le equazioni di Maxwell per il campo elettrostatico nella materia assumono la semplice forma:

$\begin{cases} \nabla \cdot \mathbf E = \displaystyle\frac{\rho}{\epsilon} & (1) \\ \nabla \times \mathbf E = 0 & (2)\end{cases} \qquad \Longrightarrow \qquad \begin{cases} \nabla \cdot \mathbf D = \rho & (3)\\ \nabla \times \mathbf D = 0 & (4)\end{cases}$

La (3) vale sempre e ovunque (nel vuoto, nella materia e indipendentemente dal regime), mentre in generale D non è conservativo, per cui si è soliti indicare fra le equazioni di Maxwell la (2) sia in elettrostatica che in elettrodinamica, modificandola con la legge di Faraday.

[modifica] Condizioni di raccordo tra dielettrici

Rimanendo nel caso di dielettrici perfetti ed isotropi, vediamo quali sono le condizioni di raccordo del campo elettrostatico quando attraversa due dielettrici di costante dielettrica relativa ε₁, ε₂. Sulla superficie di separazione prendiamo una superficie cilindrica di basi dS e altezza dl infinitesima, di ordine di grandezza superiore alla base, e applichiamo il flusso di Gauss uscente dalle basi; che ci deve dare un flusso infinitesimo nullo poiché non vi è carica all'interno:

$0 = \Phi_{\mathbf D} = \mathbf D_1 \cdot \operatorname{d} \mathbf S + \mathbf D_2 \cdot \operatorname{d} \mathbf S = \operatorname{d}S (D^{n}_{1} - D^{n}_{2})$

dove Dⁿ₁, Dⁿ₂ sono le componenti normali del campo di spostamento elettrico e allora riesce:

$D^{n}_{1} = D^{n}_{2}$

In termini di campo elettrico abbiamo:

$\epsilon_1 E^{n}_{1} = \epsilon_2 E^{n}_2 \Longrightarrow \frac{E^{n}_1}{E^{n}_2} = \frac{\epsilon_2}{\epsilon_1}$

Per la componente tangenziale del campo elettrico vale il teorema di Coulomb cioè la direzione del campo elettrico è solo normale alla superficie del conduttore e la componente tangenziale, quindi:

$E^{t}_1 = E^{t}_2$

che in termini di campo di spostamento elettrico:

$\frac{D^{t}_1}{\epsilon_1} = \frac{D^{t}_2}{\epsilon_2} \Longrightarrow \frac{D^{t}_1}{D^{t}_2} = \frac{\epsilon_1}{\epsilon_2}$

In definitiva, attraversando la superficie di separazione tra due dielettrici perfetti ed isotropi la componente normale del campo elettrico subisce una discontinuità mentre quella tangenziale non si modifica, viceversa per il campo di spostamento elettrico, mettendo insieme le due relazioni si ottiene la legge di rifrazione delle linee di forza del campo elettrico:

$\frac{E^{t}_1}{\epsilon_1 E^{n}_1} = \frac{E^{t}_2}{\epsilon_2 E^{n}_2} \Longrightarrow \frac{\tan \theta_1}{\tan \theta_2} = \frac{\epsilon_1}{\epsilon_2}$

dove

$\tan \theta = \frac{E^t}{E^n}$

è l'angolo di rifrazione.

[modifica] Campo creato da una carica in moto

Una carica q in moto con una velocità costante v crea un campo

$\mathbf{E}=\frac{1}{4\pi\varepsilon_0}\frac{1-v^2/c^2}{(1-v^2\sin^2\theta/c^2)^{3/2}}\frac{q}{r^2} \widehat{\mathbf{r}}$

dove θ è l'angolo tra la direzione di moto della carica e il raggio vettore r tracciato dalla carica al punto di osservazione del campo.

Se la carica è accelerata, all'espressione precedente si aggiunge un termine dipendente dall'accelerazione e legato alle onde elettromagnetiche irradiate dalla carica.

[modifica] Voci correlate

Portale Elettromagnetismo: accedi alle voci di Wikipedia che trattano di elettromagnetismo

Campo elettrico

Da Wikipedia, l'enciclopedia libera.

Indice

[modifica] Introduzione

[modifica] Campo elettrostatico nel vuoto

[modifica] Linee di flusso e superfici equipotenziali

[modifica] Equazioni di Maxwell per il campo elettrostatico

[modifica] Nel vuoto

[modifica] Condizioni al contorno

[modifica] In presenza di dielettrici

[modifica] Condizioni di raccordo tra dielettrici

[modifica] Campo creato da una carica in moto

[modifica] Voci correlate

Visite

Strumenti personali

Ricerca

Navigazione

comunità

Stampa/esporta

Strumenti

Altre lingue