Elettrodinamica quantistica

Teoria quantistica dei campi

Diagramma di Feynman Storia della teoria quantistica dei campi Background Teoria di gauge Teoria dei campi Simmetria di Poincaré Meccanica quantistica Rottura spontanea di simmetria Simmetria in fisica Crossing Coniugazione di carica Parità Simmetria T Strumenti Anomalia Teoria effettiva di campo Valore di aspettativa Ghost di Faddeev-Popov Diagramma di Feynman Formula di riduzione LSZ Funzione di partizione Propagatore Quantizzazione Rinormalizzazione Vuoto quantico Teorema di Wick Assiomi di Wightman Equazioni Equazione di Dirac Equazione di Klein-Gordon Equazione di Proca Equazione Wheeler-DeWitt Modello standard Interazione elettrodebole Meccanismo di Higgs Cromodinamica quantistica Elettrodinamica quantistica Teoria di Yang-Mills Teorie incomplete Gravità quantistica Teoria delle stringhe Supersimmetria Technicolor Teoria del tutto Scienziati Adler • Bethe • Bogoliubov • Callan • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg •Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Wilczek • Zimmermann • Zinn-Justin

L'elettrodinamica quantistica (o QED, dall'inglese Quantum Electro-Dynamics) è la teoria quantistica del campo elettromagnetico

La QED descrive tutti i fenomeni che coinvolgono le particelle elettricamente cariche interagenti per mezzo della forza elettromagnetica, includendo allo stesso tempo la teoria della relatività ristretta.

Matematicamente ha la struttura di una teoria di gauge abeliana con un gruppo di gauge U(1); dal punto di vista fisico questo significa che le particelle cariche interagiscono fra loro attraverso lo scambio di bosoni a massa nulla detti fotoni.

La QED è stata definita "il gioiello della fisica" per le predizioni estremamente accurate di quantità come il momento magnetico anomalo del muone e lo spostamento di Lamb-Retherford dei livelli energetici dell'idrogeno.

Storia

La prima formulazione di una teoria quantistica descrivente l'interazione fra radiazione e materia è dovuta a Paul Adrien Maurice Dirac che, negli anni venti, per primo riuscì a calcolare il coefficiente di emissione spontanea di un atomo. Dirac propose la quantizzazione del campo elettromagnetico visto come un insieme di oscillatori armonici, introducendo il concetto di operatori di creazione e distruzione di particelle. Negli anni a seguire, grazie anche ai lavori di Wolfgang Pauli, Eugene Wigner, Pascual Jordan, Werner Heisenberg e ad una formulazione elegante dell'elettrodinamica quantistica dovuta a Enrico Fermi, peraltro descritta in un lavoro classico , era chiaro che, in linea di principio, si sarebbe dovuti essere in grado di eseguire, per qualsiasi processo, i relativi calcoli. Lavori successivi di Victor Weisskopf e F. Bloch e A. Nordsieck, nel 1936 e 1937, misero in realtà in evidenza come tali calcoli fossero affidabili al più solo al primo ordine della teoria delle perturbazioni, un problema a suo tempo già evidenziato anche da Robert Oppenheimer. Agli ordini successivi comparivano quantità infinite che rendevano i calcoli senza senso mettendo così in dubbio la consistenza della teoria stessa. Sembrava esistere una incompatibilità di fondo tra relatività ristretta e meccanica quantistica senza una strada percorribile per sanarla.

Le difficoltà si acuirono sul finire degli anni quaranta. Il perfezionamento delle tecniche a microonde aveva infatti reso possibile effettuare misure di precisione, in particolare per lo spostamento dei livelli dell'atomo di idrogeno , oggi noto come spostamento di Lamb, e il momento magnetico dell'elettrone che mettevano in evidenza delle discrepanze non spiegabili dalla teoria stessa.

La prima indicazione di una possibile via di uscita fu fornita da Hans Bethe. La storia racconta che, nel 1947, mentre era in viaggio per raggiungere Shelter Island per una conferenza proprio su queste problematiche a cui avrebbe dovuto fare una presentazione, sul treno completò il primo calcolo, non-relativistico, dello spostamento delle righe dell'atomo di idrogeno come misurato da Lamb e Retherford. Nonostante le limitazioni inerenti al calcolo effettuato, l'accordo era eccellente. L'idea era semplicemente di attribuire gli infiniti a correzioni a grandezze come la massa o la carica elettrica che in realtà sono fissate ad un valore finito. Come tali, gli infiniti finiscono riassorbiti in esse e il risultato finale del calcolo è finito e in accordo con gli esperimenti. Tale procedura fu detta rinormalizzazione.

Sulla base di questa intuizione fu possibile ottenere delle formulazioni completamente covarianti e finite dell'elettrodinamica quantistica grazie ai lavori fondamentali di Sin-Itiro Tomonaga, Julian Schwinger, Richard Feynman e Freeman Dyson. I primi tre ricevettero il premio Nobel nel 1965 il loro contributo, che riguardava formulazioni covarianti e gauge-invarianti che permettevano il calcolo delle quantità osservabili. L'equivalenza tra tali formulazioni fu provata da Dyson. La procedura di rinormalizzazione, necessaria per attribuire un senso fisico ad alcune divergenze presenti negli integrali della teoria, divenne successivamente uno degli aspetti essenziali delle teorie quantistiche dei campi e un loro criterio di accettabilità.

Matematica

Formulazione Lagrangiana

La densità di lagrangiana QED per l'interazione di elettroni e positroni attraverso lo scambio di fotoni è

$\mathcal{L}=\bar\psi(i\hbar c\gamma_\mu D^\mu-mc^2)\psi -\frac{1}{4\mu_0}F_{\mu\nu}F^{\mu\nu}$

dove $\ \psi$ e la sua aggiunta di Dirac $\bar\psi$ sono i campi che rappresentano le particelle cariche, che per elettroni e positroni sono rappresentati dagli spinori di Dirac.

$D_\mu = \partial_\mu+i\frac{e}{\hbar}A_\mu$

è la derivata covariante di gauge, con e la costante di accoppiamento (uguale alla carica elementare), A_μ il potenziale vettore covariante del campo elettromagnetico ed infine

$F_{\mu\nu} = [D_\mu,D_\nu]=\partial_\mu A_\nu - \partial_\nu A_\mu$

che definisce il tensore del campo elettromagnetico.

La parte di lagrangiana che contiene il tensore F_μν del campo elettromagnetico descrive l'evoluzione del campo libero, ovvero senza alcun potenziale aggiuntivo, mentre l'equazione di Dirac con la derivata covariante di gauge descrive tanto l'evoluzione dei campi dell'elettrone e del positrone liberi, quanto la loro interazione con il campo elettromagnetico stesso.

Alla lagrangiana data è prassi aggiungere una prescrizione che determini la scelta della gauge senza introdurre tale scelta a priori sui potenziali. Tale termine prende la forma

$\delta\mathcal{L}=-\frac{\xi}{2}(\partial_\mu A^\mu)^2$

dove $\xi$ è un parametro il cui valore determina il tipo di gauge prescelto. La gauge di Landau, con il limite $\xi\rightarrow 0$, è equivalente classicamente alla gauge di Lorenz, e quando il limite è preso dopo aver quantizzato la teoria migliora il rigore di certe dimostrazioni di equivalenza e di esistenza. La maggior parte dei calcoli in teoria quantistica dei campi sono resi più semplici nella gauge di Feynman-'t Hooft per la quale è $\xi=1$. Altre scelte di gauge sono possibili come quella di Yennie con $\xi=3$.

Quantizzazione settore bosonico

La formulazione più nota dell'elettrodinamica quantistica è quella che fa ricorso alla soluzione delle equazioni del moto come insieme di oscillatori armonici. Si considerano le equazioni del moto per i campi liberi e si risolvono classicamente attraverso una serie di Fourier nella forma

$A_\mu(x)=\sum_\mathbf{k\lambda}\sqrt{\frac{\hbar}{2\omega_\mathbf{k}\varepsilon_0}}\left(\varepsilon_{\mu\lambda}\alpha_{\mathbf{k}\lambda}e^{ik\cdot x}+\varepsilon^*_{\mu\lambda}\alpha_{\mathbf{k}\lambda}^*e^{-ik\cdot x}\right).$

essendo $\lambda=1,2$ per i vettori di polarizzazione. Imponendovi la gauge di Lorenz, ma altre scelte sono possibili, e le equazioni del moto $\Box A_\mu=0$, si ottengono le condizioni $k\cdot\varepsilon_\lambda =0$ e $k^2=0$. Quindi si promuovono i coefficienti $\alpha_{\mathbf{k}\lambda}$ e $\alpha^*_{\mathbf{k}\lambda}$ ad operatori $a_{\mathbf{k}\lambda}$ e $a_{\mathbf{k}\lambda}^\dagger$ e si sostituisce tale potenziale in forma operatoriale nella corrispondente hamiltoniana

$H=\frac{1}{2}\int d^3x\left[\varepsilon_0|\dot{\mathbf{A}}|^2+\frac{1}{\mu_0}|\nabla\times \mathbf{A}|^2\right]$

che produce il seguente risultato

$H=\frac{1}{2}\sum_{\mathbf{k}\lambda}(a_{\mathbf{k}\lambda}a_{\mathbf{k}\lambda}^\dagger+a_{\mathbf{k}\lambda}^\dagger a_{\mathbf{k}\lambda})\omega_\mathbf{k}$

essendo per il campo elettromagnetico $\omega_\mathbf{k}=c|\mathbf{k}|$. Perché l'energia sia definita positiva, dobbiamo richiedere che

$[a_{\mathbf{k}\lambda},a_{\mathbf{k'}\lambda'}^\dagger]=\delta_{\mathbf{kk'}}\delta_{\lambda\lambda'}$

essendo [,] il commutatore definito come $[A,B]=AB-BA$, e dunque riconosciamo gli ordinari operatori di creazione e distruzione con il campo elettromagnetico descritto da un insieme di oscillatori armonici quantistici descriventi ognuno particelle con caratteristiche di bosoni che, per questo caso, prendono il nome di fotoni. L'hamiltoniana prende allora la forma

$H=\frac{1}{2}\sum_{\mathbf{k}\lambda}\left(a_{\mathbf{k}\lambda}^\dagger a_{\mathbf{k}\lambda}+\frac{1}{2}\right)\omega_\mathbf{k}$

in cui vediamo la comparsa di una costante infinita poiché il vettore d'onda non è limitato. Questa costante può essere eliminata osservando che siamo partiti dal limite classico per postulare la corrispondente hamiltoniana quantistica ma, dati i problemi di ordinamento degli operatori, questa scelta non può essere univoca. La costante infinita si elimina perciò con il cosiddetto prodotto normale, indicato con $:\ldots :$ che forza tutti gli operatori di creazione a sinistra. Va altresì detto che, per un volume finito, tale contributo di punto zero produce effetti fisici reali come osservato nell'effetto Casimir.

È interessante notare come, nel caso specifico della scelta della gauge di Lorenz, tale quantizzazione presenta il problema degli stati a norma negativa che implicano una violazione della unitarietà. Questo problema, che è dovuto alla simmetria di gauge di cui gode il campo elettromagnetico, può essere superato con il metodo di Gupta-Bleuler che garantisce che i calcoli effettuati forniscano un risultato fisico.

In effetti, una scelta di gauge di uso comune è quella della gauge di Coulomb in cui si impone la condizione

$\nabla\cdot\mathbf{A}=0.$

Questa scelta di gauge è manifestamente non covariante ed è la controindicazione per questa scelta specifica. Nonostante ciò, i calcoli si possono effettuare senza che per questo si abbiano inconsistenze.

Quantizzazione settore fermionico

La quantizzazione del settore fermionico procede in modo analogo, considerando le soluzioni dell'equazione di Dirac in assenza di interazione ed eseguendo uno sviluppo in serie di Fourier. Avremo

$\psi(x)=\sum_{\mathbf{p}s}\left[b_{\mathbf{p}s}u_{\mathbf{p}s}e^{-ip\cdot x/\hbar}+d^\dagger_{\mathbf{p}s}v_{\mathbf{p}s}e^{ip\cdot x/\hbar}\right]$

con le condizioni

$(c\gamma^\mu p_\mu+mc^2)u_s(\mathbf{p})=0$

e

$(-c\gamma^\mu p_\mu+mc^2)v_s(\mathbf{p})=0.$

A questo va considerato l'aggiunto di Dirac dato da $\bar\psi=\psi^\dagger\gamma^0$ essendo $\gamma^0$ una delle matrici di Dirac. Notiamo che in questo caso abbiamo operatori di creazione e distruzione per due tipi di particelle: in realtà una è l'antiparticella dell'altra. L'Hamiltoniana in questo caso dà il risultato

$H=\sum_{\mathbf{p}s}[b_{\mathbf{p}s}^\dagger b_{\mathbf{p}s}-d_{\mathbf{p}s}d_{\mathbf{p}s}^\dagger]\omega(\mathbf{p})$

essendo $\omega(\mathbf{p})=\sqrt{|\mathbf{p}|^2c^2+m^2c^4}$, e l'energia sarà definita positiva se e solo se

$\{b_{\mathbf{p}s},b_{\mathbf{p'}s'}^\dagger\}=\delta_{\mathbf{pp'}}\delta_{ss'}$

e

$\{d_{\mathbf{p}s},d_{\mathbf{p'}s'}^\dagger\}=\delta_{\mathbf{pp'}}\delta_{ss'}$

dove ora {,} è il cosiddetto anticommutatore ossia $\{A,B\}=AB+BA$. I fermioni obbediscono perciò a regole di anticommutazione. Dunque gli operatori b annichilano una particella e i d un'antiparticella e i corrispondenti coniugati creano rispettivamente una particella ed un'antiparticella. Queste avranno carica elettrica opposta.

Rappresentazione di interazione

Per eseguire i calcoli in presenza di interazione, si assume l'esistenza di un operatore di evoluzione U tale che, per un dato stato iniziale, si produca il corrispondente stato finale. L'ampiezza di transizione si calcola

$M_{fi} =\langle f|U|i \rangle.$

Un appropriato insieme di stati asintotici, finali e iniziali, è garantito dalle soluzioni delle corrispondenti teorie libere date sopra. Per determinare l'operatore di evoluzione, consideriamo di risolvere l'equazione di Schrödinger per l'elettrodinamica quantistica ricorrendo alla cosiddetta rappresentazione di interazione. In questo caso, gli stati vengono fatti evolvere nel tempo attraverso l'Hamiltoniana di interazione che nel nostro caso ha la forma

$V=e\int d^3x \bar\psi(x)\gamma^\mu\psi(x)A_\mu(x)$

e l'operatore di evoluzione prende la forma

$U=T\exp\left[-\frac{i}{\hbar}\int_{t_0}^t dt'V(t')\right]$

essendo T l'operatore cronologico. Questa espressione ha significato solo come sviluppo in serie ed abbiamo perciò uno sviluppo perturbativo per determinare le osservabili di interesse in elettrodinamica quantistica. Da notare che la determinazione delle ampiezze di probabilità come descritte qui è equivalente all'uso della matrice S. La serie perturbativa così ottenuta prende il nome di serie di Dyson. Il parametro di sviluppo è la cosiddetta costante di struttura fine data da $e^2/\hbar c$ che, alle energie di interesse, è un parametro piccolo dando formalmente senso alla serie che così si ottiene. In realtà tale sviluppo è al più asintotico ma la serie non converge.

Diagrammi di Feynman

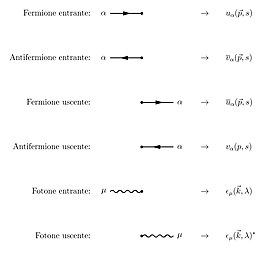
I termini della serie perturbativa possono essere descritti in modo grafico in maniera semplice utilizzando delle regole fissate a priori dette diagrammi di Feynman. Tali regole si ottengono attraverso il teorema di Wick. In elettrodinamica quantistica sono le seguenti

tenendo altresì conto che, per ogni diagramma chiuso (loop), occorre introdurre un'integrazione sui momenti $\int d^4p/(2\pi)^4$. Un tipico esempio di processo in elettrodinamica quantistica è il cosiddetto effetto Compton, ossia un urto elastico tra elettrone e fotone. Avremo i seguenti diagrammi di Feynman a descriverlo:

da cui è possibile infine ottenere la sezione d'urto del processo.

Il problema della rinormalizzabilità

Quando si va ad ordini superiori nello sviluppo in serie dell'operatore di evoluzione, ci si accorge che i diagrammi di Feynman contengono uno almeno dei seguenti tre diagrammi:

• 

  Polarizzazione del vuoto funzione $\Pi$

• 

  Auto-energia funzione $\Sigma$

• 

  Funzione vertice $\Gamma.$

Sulla base delle succitate regole di Feynman, tali diagrammi implicano un'integrazione sui momenti e questo fa comparire integrali divergenti, ossia non ben definiti matematicamente. Occorre allora introdurre una prescrizione per il trattamento di questi termini. Ciò si attua attraverso la cosiddetta procedura di rinormalizzazione. Tale procedura implica che, termini come quelli indicati portano correzioni alle costanti della teoria, quali massa e carica elettrica, che in realtà sono fissate sperimentalmente. Come tali, gli infiniti possono essere riassorbiti in tali costanti e, fatto questo, si ritrova alla fine del calcolo un valore finito per le grandezze di interesse. L'accordo che così si ha con i dati sperimentali, come ad esempio il fattore giromagnetico dell'elettrone, è eccezionalmente buono. Infatti, la rinormalizzabilità di una teoria è diventato un criterio per stabilire se una teoria dei campi quantizzati sia o meno valida. Tutte le teorie che descrivono le interazioni fondamentali sono rinormalizzabili. Incidentalmente, il fatto che ci sia un numero finito di diagrammi divergenti, tre nel caso dell'elettrodinamica quantistica, è un criterio per stabilire se una teoria sia rinormalizzabile o meno. Questo perché, quando il numero di tali diagrammi è finito, le costanti necessarie per la rinormalizzazione sono anch'esse in numero finito e questo non inficia il potere predittivo della teoria stessa.

Bibliografia

Testi tecnici

• Claude Cohen-Tannoudji, Jacques Dupont-Roc, Gilbert Grynberg, Photons and Atoms: Introduction to Quantum Electrodynamics (John Wiley & Sons 1997) ISBN 0-471-18433-0
• Feynman, R.P., Quantum Electrodynamics (Perseus Publishing, 1998), ISBN 0-201-36075-6
• Jauch, J. M., F. Rohrlich, F., The Theory of Photons and Electrons (Springer-Verlag, 1980)

Testi divulgativi

• Feynman, R.P., QED: La strana teoria della luce e della materia, Adelphi, ISBN 88-459-0719-8

Testi di storia

• Silvan Schweber, QED and the Men Who Made it: Dyson, Feynman, Schwinger, Tomonaga, (Princeton University Press, 1994), ISBN 0-691-03327-7
• Julian Schwinger, Selected Papers on Quantum Electrodynamics, (Dover, 1958), ISBN 978-0-486-60444-2

Voci correlate

• Modello Standard
• Scattering
• Diagramma di Feynman
• Propagatore
• Fotoni
• Bosone (fisica)
• Bosoni vettore
• Bosoni vettori assiali
• Equazione di Dirac
• Lista delle particelle
• Teoria di gauge

Altri progetti

• Wikiquote

• Wikiquote contiene citazioni di o su Elettrodinamica quantistica

Collegamenti esterni

• Marcello Ciafaloni Complementi di Fisica Teorica: Introduzione alla teoria dei campi (Università di Firenze)
• Roberto Casalbuoni Elettrodinamica Quantistica (Università di Firenze)
• Roberto Casalbuoni Teoria dei campi: Storia e Introduzione (Università di Firenze, 2001)

Portale Meccanica quantistica: accedi alle voci di Wikipedia che trattano di meccanica quantistica