Teoria delle stringhe
In fisica, la teoria delle stringhe (string theory, lett. "teoria delle corde") è un quadro teorico nel quale le particelle puntiformi sono sostituite da oggetti uno-dimensionali chiamati stringhe, caratterizzati da determinati "modi di vibrazione". La teoria descrive come le stringhe si propagano nello spazio e nel tempo e come interagiscono tra loro.[1] A scale di distanza maggiori della sua lunghezza, la stringa è assimilabile a una particella ordinaria, con massa, carica e le altre proprietà determinate dal suo modo di vibrazione. Poiché uno di questi corrisponde al gravitone, l'ipotetica particella mediatrice della gravità, la teoria delle stringhe è una teoria di gravità quantistica.
Questa teoria è stata studiata per la prima volta sul finire degli anni 1960 per descrivere l'interazione forte, prima di venir abbandonata in favore della cromodinamica quantistica. Successivamente, ci si accorse che le caratteristiche che la rendevano inadatta in fisica nucleare ne facevano un'ottima candidata per una teoria quantistica della gravità. La prima versione, la teoria di stringa bosonica, incorporava solo i bosoni; successivamente furono descritti anche i fermioni tramite la teoria delle superstringhe, che postula una simmetria tra le due classi di particelle, la supersimmetria. Sono state formulate cinque teorie di superstringhe coerenti, prima che negli anni 1990 venisse ipotizzato che tutte fossero casi particolari di un'unica teoria 11-dimensionale nota come teoria M. Alla fine del 1997, si scoprì la corrispondenza AdS/CFT, una relazione tra la teoria delle stringhe con una particolare teoria quantistica dei campi.
La teoria delle stringhe è una branca della fisica teorica vasta e sfaccettata che aspira a rispondere a varie domande profonde sui fondamenti della fisica. Ha contribuito a vari progressi in fisica matematica, dove è stata applicata a diversi problemi legati ai buchi neri, alla cosmologia dell'universo primordiale, alla fisica nucleare e alla fisica della materia condensata; inoltre, ha stimolato una serie di sviluppi di alcune questioni di matematica pura. Poiché potenzialmente offre una descrizione della gravità unificata con la fisica delle particelle, è una candidata per la teoria del tutto, un modello matematico che possa descrivere tutte le interazioni fondamentali in un unico quadro teorico. Tuttavia, nonostante molta ricerca sia dedicata a questo aspetto, non è ancora chiaro fino a che punto la teoria delle stringhe possa descrivere la realtà nella sua interezza.
Uno dei problemi della teoria è che la formulazione completa non è sempre definita in modo soddisfacente in tutti gli scenari teorici possibili. Un altro è che si ritiene che descriva un enorme "paesaggio" (landscape) di possibili universi ([2] universi), il che rende complicati i tentativi di identificare la fisica delle particelle all'interno della teoria. Queste difficoltà hanno portato alcuni membri della comunità scientifica a criticare questo approccio e ad avere dubbi sull'utilità di proseguire la ricerca in questo ambito.
Storia[modifica | modifica wikitesto]

La teoria delle stringhe nacque come teoria per spiegare il comportamento degli adroni. Durante gli esperimenti condotti con gli acceleratori di particelle, i fisici avevano osservato che lo spin di un adrone non è mai maggiore di un certo multiplo della radice della sua energia. Nessun semplice modello adronico, ad esempio quello che li considera composti da una serie di particelle più piccole legate da un qualche tipo di forza, spiega tali relazioni. Nel 1968 Veneziano, allora ricercatore presso il CERN di Ginevra, intuì che una vecchia formula matematica denominata funzione beta di Eulero, ideata 200 anni prima dal matematico svizzero Leonhard Euler, forniva informazioni importanti sull'interazione forte, senza però spiegare la correlazione.[3] Nel 1970 Nambu, Nielsen e Susskind tentarono una spiegazione, rappresentando la forza nucleare attraverso stringhe vibranti ad una sola dimensione; era però un'ipotesi che contraddiceva le esperienze. La comunità scientifica perse quindi interesse per la teoria e il Modello standard, con le sue particelle e i suoi campi, rimase dominante.
Poi, nel 1974, Schwarz e Scherk, e indipendentemente Yoneya, studiarono alcuni modelli della vibrazione di stringa e trovarono che le loro proprietà combaciavano esattamente con le ipotetiche particelle mediatrici della forza gravitazionale, i gravitoni. Schwarz e Scherk argomentarono che la teoria delle stringhe non aveva avuto successo perché i fisici ne avevano frainteso gli scopi. Questo condusse allo sviluppo della teoria di stringa bosonica. D'altra parte, con lo sviluppo della cromodinamica quantistica, il bisogno originario di una teoria degli adroni fu diretto verso il modello dei quark.
Si osservò che in seguito alla quantizzazione della teoria di stringa bosonica, basata sull'azione di Nambu-Goto e su quella di Poljakov, ogni diverso stato di vibrazione della stringa dava luogo a una diversa particella. Le stringhe considerate sono sia aperte, con due punti terminali definiti, che chiuse, con gli estremi congiunti a formare un anello. Tuttavia, la stringa bosonica ha vari problemi: tra gli altri, prevede l'esistenza del tachione. Questi problemi di coerenza portarono alla teoria delle superstringhe, che introduce i fermioni tramite la supersimmetria, una relazione matematica tra bosoni e fermioni.
Gli anni ottanta e i novanta sono stati protagonisti di due periodi prolifici per la teoria delle stringhe, noti come "rivoluzioni delle superstringhe". La prima avvenne tra il 1984 e il 1986 e cominciò con la scoperta dell'annullamento dell'anomalia nella teoria di stringa tipo I con il meccanismo introdotto da Green e Schwarz. Nello stesso periodo sono state presentate altre teorie di stringa, come la stringa eterotica. La seconda rivoluzione cominciò nel 1994 quando Witten e altri trovarono forti prove a dimostrazione che le differenti teorie delle superstringhe non sono che i diversi limiti di una sconosciuta teoria a undici dimensioni, chiamata teoria M.
Principi di base[modifica | modifica wikitesto]

Panoramica[modifica | modifica wikitesto]
Nel XX secolo, emersero due quadri teorici per la formulazione delle leggi della fisica. Una è la teoria della relatività generale di Albert Einstein, la teoria che spiega la forza di gravità e la struttura dello spaziotempo a livello macroscopico. L'altra è la meccanica quantistica, una formulazione completamente diversa che usa i principi della probabilità per descrivere fenomeni fisici a livello microscopico. Verso la fine degli anni 1970, questi due quadri si sono rivelati sufficienti a spiegare gran parte delle caratteristiche osservate nell'universo, dalle particelle elementari agli atomi all'evoluzione delle stelle e all'universo nel suo insieme.[4]
Nonostante i successi suddetti, ci sono ancora molti problemi che vanno risolti. Uno dei problemi più profondi della fisica moderna è la gravità quantistica.[4] La teoria della relatività generale è formulata secondo la struttura della fisica classica mentre le altre forze fondamentali sono descritte nel quadro della meccanica quantistica. Una teoria quantistica della gravità è necessaria al fine di riconciliare la relatività generale con i principi della meccanica quantistica, ma nascono difficoltà quando si tenta di applicare i metodi della teoria quantistica alla forza di gravità.[5] Oltre al problema della gravità quantistica, ci sono molti altri problemi fondamentali nella fisica dei nuclei atomici, buchi neri e l'universo primordiale.[N 1]
La teoria delle stringhe è un quadro teorico che mira a rispondere a queste domande e a molte altre. Il punto di partenza della teoria è l'idea che le particelle puntiformi della fisica delle particelle possono essere modellizzate come oggetti uno-dimensionali chiamati stringhe. La teoria delle stringhe descrive come le stringhe si propagano nello spazio e interagiscono tra di loro. In una determinata versione della teoria delle stringhe, c'è un solo tipo di stringa, che potrebbe sembrare come un piccolo anello o segmento e può vibrare in diversi modi. A scale di distanza maggiori della scala della stringa, una stringa assomiglierà a una particella ordinaria, con massa, carica e le altre proprietà determinate dal modo di vibrazione della stringa. In questo modo, tutte le diverse particelle elementari possono essere viste come stringhe vibranti. In questa teoria, uno degli stati di vibrazione dà origine al gravitone, l'ipotetica particella che media l'interazione gravitazionale: perciò la teoria delle stringhe è una teoria di gravità quantistica.[6]
Uno dei principali sviluppi degli ultimi decenni nella teoria delle stringhe è stata la scoperta di alcune "dualità", trasformazioni matematiche che identificano una teoria fisica con un'altra. Studiosi della teoria delle stringhe hanno scoperto un certo numero di queste dualità tra diverse versioni della teoria delle stringhe, e questo ha portato alla congettura che tutte le versioni coerenti della teoria delle stringhe siano sussunte in un unico quadro teorico noto come teoria M o M-teoria.[7]
Gli studi sulla teoria delle stringhe hanno anche prodotto una serie di risultati sulla natura dei buchi neri e sull'interazione gravitazionale. Ci sono alcuni paradossi che sorgono quando si cerca di capire gli aspetti quantistici dei buchi neri, e il lavoro sulla teoria delle stringhe ha cercato di chiarire questi problemi. Alla fine del 1997 questa linea di lavoro è culminata nella scoperta della corrispondenza anti-de Sitter / teoria dei campi conforme o AdS/CFT.[8] Questo è un risultato teorico che mette in relazione la teoria delle stringhe con altre teorie fisiche che sono meglio comprese a livello teorico. La corrispondenza AdS/CFT ha implicazioni per lo studio dei buchi neri e della gravità quantistica, ed è stata applicata ad altre materie, compresa la fisica nucleare[9] e della materia condensata.[10][11]
Poiché la teoria delle stringhe incorpora tutte le interazioni fondamentali, compresa la gravità, molti fisici sperano che alla fine sarà sviluppata fino al punto in cui descriverà completamente l'universo, rendendola una teoria del tutto. Uno degli obiettivi della ricerca attuale nella teoria delle stringhe è quello di trovare una soluzione della teoria che riproduca lo spettro osservato di particelle elementari, con una piccola costante cosmologica, contenente materia oscura e un meccanismo plausibile per l'inflazione cosmica. Sebbene ci siano stati progressi verso questi obiettivi, non si sa fino a che punto la teoria delle stringhe descriva il mondo reale o quanta libertà la teoria permetta nella scelta dei dettagli.[12]
Uno dei problemi della teoria delle stringhe è che la teoria completa non contiene una definizione soddisfacente per tutte le circostanze. Lo scattering di stringhe è più facilmente definita con le tecniche della teoria perturbativa, ma non è noto in generale come definire la teoria delle stringhe in maniera non perturbativa.[13] Non è chiaro neanche se ci sia un qualche principio secondo il quale la teoria scelga il suo stato di vuoto, lo stato fisico che determina le proprietà dell'universo.[14] Questi problemi hanno convinto alcuni della comunità scientifica a criticare questi approcci all'unificazione e a dubitare sul valore del proseguimento della ricerca su questo ambito di problemi.[15]
Stringhe[modifica | modifica wikitesto]
L'applicazione della meccanica quantistica agli oggetti fisici, come il campo elettromagnetico, che sono estesi nello spazio e nel tempo, è nota come teoria quantistica dei campi. In fisica delle particelle, le teorie dei campi formano la base per la comprensione delle particelle elementari modellizzate come eccitazioni nei campi fondamentali.[16]
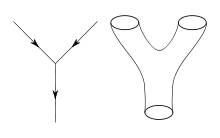
In teoria quantistica dei campi, tipicamente si calcolano le probabilità dei vari eventi fisici usando le tecniche della teoria perturbativa. Sviluppata da Richard Feynman e altri nella prima metà del XX secolo, la teoria quantistica dei campi perturbativa usa particolari diagrammi noti come diagrammi di Feynman per organizzare i calcoli. Si immagina che questi diagrammi rappresentano i percorsi delle particelle puntiformi e le loro interazioni.[16]
Il punto di partenza della teoria delle stringhe è l'idea che le particelle puntiformi possono essere modellizzate come oggetti uno-dimensionali chiamati stringhe.[17] L'interazione delle stringhe è più facilmente definita con le tecniche della teoria delle perturbazioni usate nell'ordinaria teoria quantistica dei campi. Al livello dei diagrammi di Feynman, questo significa sostituire il diagramma uno-dimensionale con una superficie due-dimensionale (2D) che rappresenta il moto di una stringa.[18] A differenza della teoria dei campi, la teoria delle stringhe non ha una definizione completa non perturbativa, per cui le risposte a molte domande teoriche rimangono fuori portata.[19]
Nelle teorie della fisica delle particelle basate sulla teoria delle stringhe, la scala di lunghezza caratteristica delle stringhe è assunta essere dell'ordine della lunghezza di Planck, pari a 10−35 metri, la scala alla quale gli effetti della gravità quantistica sono ritenuti significativi.[18] Su scale di lunghezza molto maggiori, come le scale osservabili nei laboratori di fisica, tali oggetti sarebbero indistinguibili dalle particelle puntiformi, e lo stato vibrazionale della stringa determinerebbe il tipo della particella. Uno degli stati vibrazionali di una stringa corrisponde al gravitone, l'ipotetica particella che media l'interazione gravitazionale: perciò la teoria delle stringhe è una teoria di gravità quantistica.[6]
La versione originale della teoria delle stringhe era la teoria delle stringhe bosoniche, ma questa versione descriveva solo i bosoni, una classe di particelle che trasmettono forze tra le particelle di materia, o fermioni. La teoria delle stringhe bosoniche è stata infine sostituita da teorie chiamate teorie delle superstringhe. Queste teorie descrivono sia bosoni che fermioni, e incorporano un'idea teorica chiamata supersimmetria. Nelle teorie con supersimmetria, ogni bosone ha una controparte che è un fermione, e viceversa.[20]
Ci sono diverse versioni della teoria delle superstringhe: tipo I, tipo IIA, tipo IIB, e due sapori della teoria di stringa eterotica (SO(32) e E8 × E8). Le diverse teorie permettono diversi tipi di stringhe e le particelle che emergono a basse energie mostrano diverse simmetrie. Per esempio, la teoria di tipo I comprende sia stringhe aperte (segmenti con punti estremi) e stringhe chiuse (che formano anelli), mentre le teorie di tipo IIA, IIB e eterotiche comprendono solo stringhe chiuse.[21]
Dimensioni extra[modifica | modifica wikitesto]

Nella vita quotidiana, ci sono tre dimensioni familiari (3D) dello spazio: altezza, larghezza e lunghezza. La teoria della relatività ristretta tratta il tempo come una dimensione alla pari con le tre dimensioni spaziali, per cui lo spazio e il tempo non sono modellizzati come entità separate, ma sono unificati in uno spaziotempo quadridimensionale (4D). Va considerato inoltre che nella relatività generale la gravità è vista come una conseguenza della geometria dello spaziotempo.[22]
A dispetto del fatto che l'universo è ben descritto da uno spaziotempo 4D, ci sono molte motivazioni per cui i fisici considerano teorie con ulteriori dimensioni. In alcuni casi, modellizzando lo spaziotempo in un numero superiore di dimensioni una teoria diventa matematicamente più trattabile[N 2]; ci sono poi situazioni dove le teorie con due o tre dimensioni spaziotemporali aggiuntive sono utili per descrivere fenomeni in fisica della materia condensata.[16] In questi scenari le dimensioni aggiuntive dello spaziotempo che potrebbero esistere oltre alle 4 canoniche in qualche modo non hanno potuto ancora essere osservate negli esperimenti.[23]
Le varie teorie di stringa richiedono dimensioni extra dello spaziotempo per essere coerenti dal punto di vista matematico. Nel caso delle stringhe bosoniche, lo spaziotempo ha 26 dimensioni, mentre per le superstringhe è 10-dimensionale e in teoria M le dimensioni sono 11.

La compattificazione è un modo di modificare il numero di dimensioni in una teoria fisica: si suppone che alcune delle dimensioni extra si "chiudano" su sé stesse a formare dei cerchi.[24] Nel limite in cui queste dimensioni arrotolate diventano molto piccole, si ottiene una teoria in cui lo spaziotempo ha effettivamente un numero inferiore di dimensioni rilevabili. Un'analogia diffusa per questo procedimento è considerare un oggetto multidimensionale come un tubo da giardino. Se il tubo è visto da una distanza sufficiente, sembra avere solo una dimensione, la sua lunghezza, tuttavia, quando ci si avvicina, si scopre che esso contiene una seconda dimensione, la sua circonferenza. Così, una formica che cammini sulla superficie interna del tubo si muove in due dimensioni.
La compattificazione può essere usata per costruire modelli in cui lo spaziotempo è effettivamente quadridimensionale. Tuttavia, non tutti i modi di compattare le dimensioni producono un modello con le proprietà giuste per descrivere la natura. In un modello in grado di descrivere correttamente la fisica delle particelle, le dimensioni extra compattate devono assumere la forma di varietà di Calabi-Yau,[24] un particolare spazio topologico dotato tipicamente di sei dimensioni. Prende il nome dai matematici Eugenio Calabi e Yau Shing-Tung.[25]
Un altro approccio per ridurre il numero di dimensioni è il cosiddetto scenario "mondo-brana", in cui si assume che l'universo osservabile sia un sottospazio quadridimensionale di uno spazio di dimensioni superiori. In tali modelli, i bosoni della fisica delle particelle nascono da stringhe aperte con gli estremi attaccati al sottospazio quadridimensionale, mentre la gravità nasce da stringhe chiuse che si propagano attraverso lo spazio più grande. Questa idea gioca un importante ruolo nei tentativi di sviluppare modelli basati sulla teoria delle stringhe in grado di descrivere la fisica del mondo reale, e fornisce una spiegazione naturale per la debolezza della gravità rispetto alle altre forze fondamentali.[26]
Dualità[modifica | modifica wikitesto]

Un fatto degno di nota della teoria delle stringhe è che le diverse versioni della teoria risultano essere tutte correlate in modi altamente non banali. Una delle relazioni che possono esistere tra diverse teorie delle stringhe è chiamata S-dualità. Si tratta di una relazione che dice che un insieme di particelle fortemente interagenti in una teoria può, in alcuni casi, essere vista come un insieme di particelle debolmente interagenti in una teoria completamente diversa. In parole povere, si dice che un insieme di particelle è fortemente interagente se si combina e decade spesso e debolmente interagente se lo fa raramente. La teoria di stringa di tipo I risulta essere equivalente secondo la S-dualità alla teoria delle stringhe eterotica SO(32). Allo stesso modo, la teoria delle stringhe di tipo IIB è legata a se stessa in modo non banale dalla S-dualità.[27]
Un'altra relazione tra diverse teorie delle stringhe è la T-dualità, in cui si considerano le stringhe che si propagano intorno ad una dimensione circolare extra. La T-dualità afferma che una stringa che si propaga intorno ad un cerchio di raggio R è equivalente ad una stringa che si propaga intorno ad un cerchio di raggio 1/R nel senso che tutte le quantità osservabili in una descrizione sono identificate con le quantità nella descrizione duale. Per esempio, una stringa ha una quantità di moto mentre si propaga intorno a un cerchio, e può anche avvolgersi intorno al cerchio una o più volte. Il numero di volte che la stringa si avvolge intorno a un cerchio è chiamato numero di avvolgimenti. Se una stringa ha quantità di moto p e numero di avvolgimenti n in una descrizione, avrà quantità di moto n e numero di avvolgimenti p nella descrizione duale. Per esempio, la teoria delle stringhe di tipo IIA è equivalente alla teoria delle stringhe di tipo IIB attraverso la T-dualità, e anche le due versioni della teoria delle stringhe eterotiche sono correlate dalla T-dualità.[27]
In generale, il termine dualità si riferisce a una situazione in cui due sistemi fisici apparentemente diversi risultano essere equivalenti in modo non banale. Due teorie legate da una dualità non devono necessariamente essere teorie delle stringhe. Per esempio, la dualità di Montonen-Olive è un esempio di relazione di dualità S tra teorie quantistiche di campo. La corrispondenza AdS/CFT è un esempio di dualità che mette in relazione la teoria delle stringhe con una teoria quantistica di campo. Se due teorie sono collegate da una dualità, significa che una teoria può essere trasformata in qualche modo in modo da finire per assomigliare all'altra teoria. Si dice allora che le due teorie sono duali l'una all'altra sotto la trasformazione. Detto altrimenti, le due teorie sono descrizioni matematicamente diverse degli stessi fenomeni.[28]
Brane[modifica | modifica wikitesto]

In teoria delle stringhe e altre teorie correlate, una brana è un oggetto fisico che generalizza la nozione di una particella puntiforme a dimensioni superiori. Per esempio, una particella puntiforme può essere vista come una brana di dimensione zero, mentre una stringa può essere vista come una brana di dimensione uno, ed è anche possibile considerare brane a dimensioni superiori. Nella dimensione p, sono chiamate p-brane. La parola "brana" deriva dalla parola "membrana" che si riferisce a una brana bidimensionale.[29]
Le brane sono oggetti dinamici che possono propagarsi nello spazio-tempo secondo le regole della meccanica quantistica. Hanno massa e possono avere altri attributi come la carica. Una p-brana spazia su un volume (p+1)-dimensionale nello spaziotempo chiamato il suo volume di mondo (worldvolume). I fisici studiano spesso campi analoghi al campo elettromagnetico che vivono sul volume di mondo di una brana.[29]
Nella teoria delle stringhe, le D-brane sono una classe importante di brane che sorgono quando si considerano le stringhe aperte. Quando una stringa aperta si propaga attraverso lo spaziotempo, i suoi punti finali devono trovarsi su una D-brana. La lettera "D" in D-brana si riferisce a una certa condizione matematica sul sistema nota come condizione al contorno di Dirichlet. Lo studio delle D-brane nella teoria delle stringhe ha portato a risultati importanti come la corrispondenza AdS/CFT, che ha fatto luce su molti problemi della teoria quantistica dei campi.[29]
Tipi di teorie[modifica | modifica wikitesto]
| Tipo | Dimensioni | Dettagli |
|---|---|---|
| Bosonica | 26 | Solo bosoni, nessun fermione, quindi solo forze, niente materia, sia stringhe chiuse che aperte; incongruenza maggiore: una particella con massa immaginaria, chiamata tachione |
| I | 10 | Supersimmetria tra forze e materia, con stringhe sia aperte che chiuse, nessun tachione, gruppo simmetrico SO(32) |
| IIA | 10 | Supersimmetria tra forze e materia, solo stringhe chiuse, nessun tachione, fermioni privi di massa con spin in entrambe le direzioni (non-chirali) |
| IIB | 10 | Supersimmetria tra forze e materia, solo stringhe chiuse, nessun tachione, fermioni privi di massa con spin in un'unica direzione (chirali) |
| HO | 10 | Supersimmetria tra forze e materia, solo stringhe chiuse, eterotiche, cioè le stringhe che si muovono verso destra differiscono da quelle che si muovono a sinistra, nessun tachione, gruppo simmetrico SO(32) |
| HE | 10 | Supersimmetria tra forze e materia, solo stringhe chiuse, eterotiche, cioè le stringhe che si muovono verso destra differiscono da quelle che si muovono a sinistra, nessun tachione, gruppo simmetrico E8×E8 |
Teoria delle stringhe bosoniche[modifica | modifica wikitesto]
La teoria di stringa bosonica è la teoria delle stringhe originale e la più semplice. Il nome deriva dal fatto che descrive solo particelle bosoniche. Questa teoria implica che le dimensioni dello spaziotempo siano 26 e prevede l'esistenza dei tachioni, che sono un tipo di particella ipotetica di massa immaginaria; questo è un segno di instabilità della teoria che rende quest'ultima incapace di descrivere la realtà. Tuttavia, la struttura matematica è abbastanza simile alle teorie più sofisticate, e predice l'esistenza di una particella identificabile con il gravitone, facendo di lei un esempio di teoria di gravità quantistica.
Teoria delle superstringhe[modifica | modifica wikitesto]
La teoria delle superstringhe è una particolare teoria che incorpora i fermioni, supponendo la presenza di una supersimmetria tra i due tipi di particelle sul foglio delle stringhe. Di fatto esistono cinque teorie delle superstringhe. Tutte e cinque prevedono un universo con 10 dimensioni (nove spaziali e una temporale) e non possiedono tachioni.
Altri oggetti sono presenti nelle teorie delle stringhe, ad esempio le Dp-brane, dove p è il numero di dimensioni spaziali dell'oggetto. Sono delle ipersuperfici definite come gli spazi sui quali sono fissati gli estremi delle stringhe aperte. Lo studio dello spettro mostra che le brane D1, D3, D5 e D7 possono essere incorporate in uno spazio descritto dalla teoria IIB, mentre in uno spazio dove vivono le stringhe IIA si possono introdurre le brane D0, D2, D4, D6 e D8. Le D1 hanno lo stesso numero di dimensioni di una stringa fondamentale, e di solito sono indicate con F1). Pur essendo due oggetti distinti, la simmetria chiamata S-dualità, che ha subito un gran numero di verifiche indirette, ha la proprietà di scambiare D1-brane con F1-brane.
Teoria M[modifica | modifica wikitesto]
Nel 1995, al congresso Strings '95, Edward Witten, mettendo assieme una serie di indizi, affermò l'esistenza di una teoria 11-dimensionale che soggiace tutte e cinque le teorie delle superstringhe e la supergravità a 11 dimensioni e che queste ultime sono casi limite di questa nuova teoria.[30] La chiamò teoria M, dove «la M significa "magia", "mistero" o "matrice", a seconda dei gusti».
Possibili prove[modifica | modifica wikitesto]
L'uomo non possiede la tecnologia per osservare le stringhe, in quanto dai modelli matematici dovrebbero avere dimensioni intorno alla lunghezza di Planck, circa 10−35 metri. Le concentrazioni di energia richieste a tali dimensioni sembrano definitivamente fuori dalla portata di qualsiasi strumento attuale o futuro.
Anisotropie nel fondo cosmico e stringhe cosmiche[modifica | modifica wikitesto]
Potremmo alla fine essere in grado di osservare le stringhe in maniera significativa, o almeno ottenere informazioni sostanziali osservando fenomeni cosmologici che possano chiarire gli aspetti della fisica delle stringhe. In particolare, visti i dati dell'esperimento WMAP, si suppone che gli esperimenti del satellite Planck dovrebbero far luce sulle condizioni iniziali dell'Universo, misurando con estrema precisione le anisotropie del fondo a microonde.
Nei primi anni 2000 i teorici delle stringhe hanno riportato in auge un vecchio concetto: la stringa cosmica. Le stringhe cosmiche, originariamente introdotte negli anni ottanta, sono oggetti differenti da quelli delle teorie delle superstringhe. Per alcuni anni le stringhe cosmiche sono state un modello molto in voga per spiegare vari fenomeni cosmici, come ad esempio la formazione delle galassie nelle prime epoche dell'universo. Ma esperimenti successivi — ed in particolare più precise misurazioni della radiazione cosmica di fondo — non sono stati in grado di confermare le ipotesi del modello delle stringhe cosmiche che per questo motivo fu abbandonato. Alcuni anni più tardi è stato osservato che l'universo in espansione può aver "stirato" una stringa "fondamentale" (del tipo che viene ipotizzato nella teoria delle superstringhe) fino ad allungarla a dimensioni macroscopiche. Una stringa così allungata può assumere molte delle proprietà della stringa del "vecchio" tipo, rendendo attuali ed utili i precedenti calcoli. Inoltre le moderne teorie delle superstringhe ipotizzano altri oggetti che potrebbero facilmente essere interpretati come stringhe cosmiche, ad esempio le D1-brane (dette anche D-stringhe) monodimensionali fortemente allungate. Come fa notare il fisico teorico Tom Kibble "i cosmologi delle teorie delle stringhe hanno scoperto stringhe cosmiche rovistando in ogni dove nel sottobosco". Le precedenti proposte metodologiche per ricercare le stringhe cosmiche possono essere ora utilizzate per investigare la teoria delle superstringhe. Ad esempio gli astronomi hanno anche riscontri numerosi di cosa potrebbe essere la lente gravitazionale indotta da stringhe.
Superstringhe, D-brane ed altri tipi di stringhe stirate fino alla scala intergalattica emettono onde gravitazionali che potrebbero essere rilevate utilizzando esperimenti del tipo LIGO. Esse possono anche provocare lievi irregolarità nella radiazione cosmica di fondo ancora impossibili da rilevare ma probabilmente osservabili in un prossimo futuro.
Sebbene accattivanti, queste prospettive cosmologiche sono carenti sotto un punto di vista: come precedentemente detto, la verifica sperimentale di una teoria richiede che i test siano in grado, in via di principio, di "rendere falsa" la teoria stessa. Per esempio, se si osservasse che il Sole durante un'eclissi solare non deflette la luce a causa della sua interazione gravitazionale, la teoria della relatività generale di Einstein sarebbe dimostrata erronea (naturalmente escludendo la possibilità di un errore nell'esperimento). Il fatto di non trovare stringhe cosmiche non dimostrerebbe che la teoria delle stringhe è fondamentalmente sbagliata ma solo che è sbagliata l'idea specifica di una stringa fortemente allungata a livello cosmico. Sebbene si possano fare, in via teorica, numerose misurazioni che dimostrino che la teoria delle stringhe è valida, fino ad ora gli scienziati non hanno escogitato dei "test" rigorosi.
Particelle a carica elettrica frazionaria[modifica | modifica wikitesto]
Alcuni dei modelli di spazi di Calabi-Yau prevedono la possibile esistenza di particelle dotate di carica elettrica frazionaria, secondo rapporti diversi da quelli finora attribuiti alle cariche quark e antiquark.
L'osservazione futura di tali particelle potrebbe essere una traccia della validità della teoria, sebbene non decisiva, visto che la sua eventuale fondatezza rimane compatibile anche con l'inesistenza di tali cariche frazionarie.
Critiche[modifica | modifica wikitesto]
Numero di soluzioni possibili[modifica | modifica wikitesto]
Per costruire i modelli di fisica delle particelle basati sulla teoria delle stringhe, i fisici cominciano tipicamente a specificare una forma per le dimensioni extra dello spaziotempo. Ognuna di queste forme corrisponde a un differente universo o "stato di vuoto", con una diversa collezione di particelle e forze. La teoria delle stringhe come è attualmente compresa ha un enorme numero di stati di vuoto, stimato intorno ai 10500, che potrebbe essere sufficientemente alto per dare spazio a quasi ogni fenomeno che potrebbe venire osservato a basse energie.[31]
Molti critici della teoria delle stringhe hanno espresso preoccupazioni circa il grande numero di universi possibili descritti dalla teoria delle stringhe. Nel suo libro Not Even Wrong, Peter Woit, docente presso il dipartimento di matematica della Columbia University, ha arguito che il gran numero dei diversi scenari possibili rende impossibile che la teoria delle stringhe possa essere un paradigma per costruire modelli della fisica delle particelle. Secondo Woit,
«The possible existence of, say, 10500 consistent different vacuum states for superstring theory probably destroys the hope of using the theory to predict anything. If one picks among this large set just those states whose properties agree with present experimental observations, it is likely there still will be such a large number of these that one can get just about whatever value one wants for the results of any new observation.[32]»
«L'esistenza possibile di, diciamo, 10500 stati di vuoto diversi consistenti per la teoria delle superstringhe probabilmente distrugge la speranza di usare la teoria per predire qualcosa. Se si scelgono in questo insieme solo quegli stati le cui proprietà concordano con le osservazioni sperimentali, è probabile ci sarà ancora un numero talmente grande di questi che si può ottenere il valore che si vuole per i risultati di qualsivoglia nuova osservazione»
Alcuni fisici ritengono che questo grande numero di soluzioni sia in realtà un vantaggio perché può permettere una spiegazione antropica naturale dei valori osservati delle costanti fisiche, in particolare il piccolo valore della costante cosmologica.[32] Il principio antropico è l'idea che alcuni dei numeri che appaiono nelle leggi della fisica non sono fissati da nessun principio fondamentale ma devono essere compatibili con l'evoluzione della vita intelligente. Nel 1987, Steven Weinberg pubblicò un articolo in cui sosteneva che la costante cosmologica non poteva essere troppo grande, altrimenti le galassie e la vita intelligente non avrebbero potuto svilupparsi.[33] Weinberg suggerì inoltre che ci potrebbe essere un enorme numero di possibili universi coerenti, ognuno con un diverso valore della costante cosmologica, e le osservazioni indicano un piccolo valore della costante cosmologica solo perché agli esseri umani capita di vivere in un universo che ha permesso l'esistenza di vita intelligente, e quindi di osservatori.[34]
Anche il fisico teorico Leonard Susskind afferma che la teoria delle stringhe fornisce una spiegazione antropica naturale per il piccolo valore della costante cosmologica.[35] Secondo Susskind, i diversi stati di vuoto previsti dalla teoria potrebbero essere considerati come universi all'interno di un multiverso. Il fatto che l'universo osservato abbia una piccola costante cosmologica è semplicemente una conseguenza tautologica del fatto che un piccolo valore è necessario per l'esistenza della vita.[36] Molti importanti teorici non concordano con l'affermazione di Susskind.[37] Secondo Woit, "in questo caso [il ragionamento antropico] non è altro che una giustificazione per il fallimento. Le idee scientifiche speculative falliscono non solo quando fanno predizioni errate, ma anche quando si rivelano insulse e incapaci di predire alcunché".[38]
Verificabilità[modifica | modifica wikitesto]
A tutt'oggi, la teoria delle stringhe non è verificabile, anche se ci sono aspettative che nuove e più precise misurazioni delle anisotropie della radiazione cosmica di fondo, possano dare le prime conferme indirette. Indubbiamente non è l'unica teoria in sviluppo a soffrire di questa difficoltà; qualunque nuovo sviluppo può passare attraverso una fase di non verificabilità prima di essere definitivamente accettato o respinto.
Come Richard Feynman scrive ne Il carattere della Legge Fisica, il test chiave di una teoria scientifica è verificare se le sue conseguenze sono in accordo con le misurazioni ottenute sperimentalmente. Non importa chi abbia inventato la teoria, "quale sia il suo nome", e neanche quanto la teoria possa essere esteticamente attraente: "se essa non è in accordo con la realtà sperimentale, essa è sbagliata" (ovviamente, ci possono essere fattori collaterali: qualcosa può essere andato male nell'esperimento, o forse chi stava valutando le conseguenze della teoria ha commesso un errore: tutte queste possibilità devono essere verificate, il che comporta un tempo non trascurabile). Nessuna versione della teoria delle stringhe ha avanzato una previsione che differisca da quelle di altre teorie - almeno, non in una maniera che si possa verificare sperimentalmente. In questo senso, la teoria delle stringhe è ancora in uno "stato larvale": essa possiede molte caratteristiche di interesse matematico, e può davvero diventare estremamente importante per la comprensione dell'Universo, ma richiede ulteriori sviluppi prima di poter diventare verificabile. Questi sviluppi possono essere nella teoria stessa, come nuovi metodi per eseguire i calcoli e derivare le predizioni, o possono consistere in progressi nelle scienze sperimentali, che possono rendere misurabili quantità che al momento non lo sono.
Si potrebbe tuttavia verificare la veridicità della teoria indirettamente analizzando i gravitoni. Gli attuali acceleratori di particelle non sono in grado di tracciare il momento in cui un gravitone sfugge per passare a una brana vicina.
Falsificabilità[modifica | modifica wikitesto]
Considerare la teoria sotto il solo profilo della sua verificabilità è comunque estremamente riduttivo ed apre il campo ad una serie di problemi. Non è infatti sufficiente l'accordo con i dati sperimentali per conferire lo status di teoria scientifica. Tutte le mere descrizioni di un fenomeno (sofisticatissime o banalissime come: "il sole sorge ogni mattina") sono in accordo con i dati sperimentali, e forniscono anche previsioni verificabili, ma senza essere per questo considerate teorie scientifiche.
La teoria delle stringhe ha dato delle predizioni ben precise tramite la corrispondenza AdS/CFT sulla viscosità dei fluidi fortemente accoppiati che sono in accordo[39] con i dati sperimentali osservati al RHIC.
Note[modifica | modifica wikitesto]
- ^ Physics World, "Stringscape", p. 39, su download.iop.org. URL consultato il 24 aprile 2012 (archiviato dall'url originale il 25 aprile 2012).
- ^ La teoria delle stringhe produce meno universi del previsto, su lescienze.it, 6 agosto 2018.
- ^ LA MADRE DI TUTTE LE TEORIE, su cosediscienza.it, Cose di Scienza. URL consultato il 14 giugno 2013 (archiviato dall'url originale il 26 luglio 2013).
- ^ a b Becker, Becker e Schwarz, p. 1.
- ^ Zwiebach, p. 6.
- ^ a b Becker, Becker e Schwarz, pp. 2–3.
- ^ Becker, Becker e Schwarz, pp. 9–12.
- ^ Becker, Becker e Schwarz, pp. 14–15.
- ^ Igor Klebanov e Juan Maldacena, Solving Quantum Field Theories via Curved Spacetimes (PDF), in Physics Today, vol. 62, n. 1, 2009, pp. 28–33 [28], Bibcode:2009PhT....62a..28K, DOI:10.1063/1.3074260. URL consultato il 29 dicembre 2016 (archiviato dall'url originale il 2 luglio 2013).
- ^ Subir Sachdev, Strange and stringy, in Scientific American, vol. 308, n. 44, 2013, pp. 44–51 [51], Bibcode:2012SciAm.308a..44S, DOI:10.1038/scientificamerican0113-44, PMID 23342451.
- ^ Zeeya Merali, Collaborative physics: string theory finds a bench mate, in Nature, vol. 478, n. 7369, 2011, pp. 302–304 [303], Bibcode:2011Natur.478..302M, DOI:10.1038/478302a, PMID 22012369.
- ^ Becker, Becker e Schwarz, pp. 3, 15–16.
- ^ Becker, Becker e Schwarz, p. 8.
- ^ Becker, Becker e Schwarz, pp. 13–14.
- ^ Woit.
- ^ a b c Anthony Zee, Parts V and VI, in Quantum Field Theory in a Nutshell, 2nd, Princeton University Press, 2010, ISBN 978-0-691-14034-6.
- ^ Becker, Becker e Schwarz, p. 2.
- ^ a b Becker, Becker e Schwarz, p. 6.
- ^ Zwiebach, p. 12.
- ^ Becker, Becker e Schwarz, p. 4.
- ^ Zwiebach, p. 324.
- ^ Wald, p. 4.
- ^ Zwiebach, p. 9.
- ^ a b Yau e Nadis, cap. 6.
- ^ Yau e Nadis, p. ix.
- ^ Lisa Randall e Raman Sundrum, An alternative to compactification, in Physical Review Letters, vol. 83, n. 23, 1999, pp. 4690–4693, Bibcode:1999PhRvL..83.4690R, DOI:10.1103/PhysRevLett.83.4690, arXiv:hep-th/9906064.
- ^ a b Becker, Becker e Schwarz.
- ^ Zwiebach, p. 376.
- ^ a b c Moore, Gregory, What is ... a Brane? (PDF), in Notices of the AMS, vol. 52, 2005, pp. 214–215. URL consultato il 29 dicembre 2016.
- ^ Edward Witten, Some Comments On String Dynamics (PDF), 23 luglio 1995.
- ^ Woit, pp. 240–242.
- ^ a b Woit, p. 242.
- ^ Steven Weinberg, Anthropic bound on the cosmological constant, in Physical Review Letters, vol. 59, n. 22, 1987, pp. 2607–2610, Bibcode:1987PhRvL..59.2607W, DOI:10.1103/PhysRevLett.59.2607, PMID 10035596.
- ^ Woit, p. 243.
- ^ Leonard Susskind, The Cosmic Landscape: String Theory and the Illusion of Intelligent Design, Back Bay Books, 2005, ISBN 978-0316013338.
- ^ Woit, pp. 242–243.
- ^ Woit, p. 240.
- ^ Woit, p. 249.
- ^ STRINGS LINK THE ULTRACOLD WITH THE SUPERHOT, su sciencenews.org, Science News. URL consultato il 4 maggio 2019 (archiviato dall'url originale il 22 luglio 2012).
- Annotazioni
- ^ Ad esempio, non sono ancora compresi il fenomeno del confinamento di colore, i paradossi dei buchi neri e l'origine dell'energia oscura.
- ^ Ad esempio, nel contesto della corrispondenza AdS/CFT, i teorici spesso formulano o studiano teorie di gravità in un numero non fisico di dimensioni spaziotemporali.
Bibliografia[modifica | modifica wikitesto]
- Katrin Becker, Melanie Becker e John Schwarz, String theory and M-theory: A modern introduction, Cambridge University Press, 2007, ISBN 978-0-521-86069-7.
- Michael Duff, The theory formerly known as strings, in Scientific American, vol. 278, n. 2, 1998, pp. 64–9, Bibcode:1998SciAm.278b..64D, DOI:10.1038/scientificamerican0298-64.
- Terry Gannon, Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms, and Physics, Cambridge University Press.
- Kentaro Hori, Sheldon Katz, Albrecht Klemm, Rahul Pandharipande, Richard Thomas, Cumrun Vafa, Ravi Vakil e Eric Zaslow (a cura di), Mirror Symmetry (PDF), Clay Mathematics Monographs, vol. 1, American Mathematical Society, 2003, ISBN 978-0-8218-2955-4 (archiviato dall'url originale il 19 settembre 2006).
- Juan Maldacena, The Illusion of Gravity (PDF), in Scientific American, vol. 293, n. 5, 2005, pp. 56–63, Bibcode:2005SciAm.293e..56M, DOI:10.1038/scientificamerican1105-56, PMID 16318027. URL consultato il 29 dicembre 2016 (archiviato dall'url originale il 1º novembre 2014).
- Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Knopf, 2005, ISBN 978-0-679-45443-4.
- Lee Smolin, The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next, New York, Houghton Mifflin Co., 2006, ISBN 978-0-618-55105-7.
- Robert Wald, General Relativity, University of Chicago Press, 1984, ISBN 978-0-226-87033-5.
- Peter Woit, Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law, Basic Books, 2006, p. 105, ISBN 978-0-465-09275-8.
- Yau Shing-Tung e Steve Nadis, The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions, Basic Books, 2010, ISBN 978-0-465-02023-2.
- Barton Zwiebach, A First Course in String Theory, Cambridge University Press, 2009, ISBN 978-0-521-88032-9. (correzioni online)
- Testi divulgativi
- Particelle, stringhe e altro di Warren Siegel, Di Renzo Editore (2008), ISBN 88-8323-204-6.
- L'universo elegante di Brian Greene, Einaudi (2000), ISBN 88-06-15523-7.
- La trama del cosmo di Brian Greene, Einaudi (2004), ISBN 88-06-18091-6
- La materia-specchio di Robert Foot, Macro Edizioni (2005) ISBN 88-7507-448-8
- Un universo diverso di Robert Laughlin, Codice Edizioni (2006) ISBN 88-7578-033-1
- Il cervello quantico di Jeffrey Satinover, Macro Edizioni (2002) ISBN 88-7507-408-9
- Il giardino delle particelle di Gordon Kane, Tea Edizioni (1997) ISBN 88-502-0125-7
- Il paesaggio cosmico: Dalla teoria delle stringhe al megaverso di Leonard Susskind, Adelphi (2006), ISBN 88-459-2153-0
- Neanche sbagliata. Il fallimento della teoria delle stringhe e la corsa all'unificazione delle leggi della fisica di Peter Woit, Codice Edizioni, (2007) ISBN 88-7578-072-2
- Rischiare con Dio (dopo Einstein) di Antonino Palumbo, Edizioni Scientifiche Italiane, (2006), ISBN 88-495-1257-0
- L'unificazione della conoscenza di Antonino Palumbo, Edizioni Scientifiche Italiane, (2008), ISBN 978-88-495-1745-3
- L'arte della fisica. Stringhe, superstringhe e teoria unificata dei campi di S. James Gates Jr, Di Renzo Edizioni (2006)
- Manuali
- Michael Green, John Schwarz and Edward Witten, Superstring theory, Cambridge University Press (1987). Il libro di testo originale.
- Vol. 1: Introduction, ISBN 0-521-35752-7.
- Vol. 2: Loop amplitudes, anomalies and phenomenology, ISBN 0-521-35753-5.
- Johnson, Clifford, D-branes, Cambridge University Press (2003). ISBN 0-521-80912-6.
- Joseph Polchinski, String Theory, Cambridge University Press (1998). Un testo moderno.
- Vol. 1: An introduction to the bosonic string, ISBN 0-521-63303-6.
- Vol. 2: Superstring theory and beyond, ISBN 0-521-63304-4.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikiquote contiene citazioni sulla teoria delle stringhe
Wikiquote contiene citazioni sulla teoria delle stringhe Wikimedia Commons contiene immagini o altri file sulla teoria delle stringhe
Wikimedia Commons contiene immagini o altri file sulla teoria delle stringhe
Collegamenti esterni[modifica | modifica wikitesto]
- stringhe, teorìa delle / La grande scienza. Teoria delle stringhe / La grande scienza. Teoria delle stringhe: una testimonianza, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- Teoria delle stringhe, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- (EN) Brian Greene, string theory, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- Tutto sulle stringhe, su scienzapertutti.lnf.infn.it.
- Un mondo fatto a stringhe su Focus
- (EN) The String Theory Web Site – ottimo sito con formule matematiche (per esperti)
- (EN) Unstrung – articolo di Jim Holt, per lo più critico, su The New Yorker
- (EN) Superstring theory - guida online
- (EN) Beyond String Theory - progetto in corso con vari aspetti della teoria delle stringhe
- (EN) The Elegant Universe - documentario NOVA di Brian Greene
- (EN) The Symphony of Everything – introduzione interattiva alla teoria delle stringhe
- (EN) Cosmic strings reborn? di Tom Kibble, conferenza del settembre 2004
- (EN) SCI.physics.STRINGS – Newsgroup dedicato alla teoria delle stringhe
- (EN) Resource Letter – una guida per studenti alla letteratura sulla teoria delle stringhe
- (EN) Superstrings! – tutorial online
- (EN) A popular blog on string theory – blog sulla teoria delle stringhe
- (EN) Is string theory even wrong? – critica alla teoria delle stringhe
- Davide Mauro, Dal Brahman alla Teoria delle Stringhe: la via orientale della fisica, su elapsus.it. URL consultato il 10 gennaio 2017.
| Controllo di autorità | Thesaurus BNCF 44297 · LCCN (EN) sh85129017 · GND (DE) 4224278-2 · BNF (FR) cb12277630h (data) · J9U (EN, HE) 987007541193405171 |
|---|
