Modello standard

Teoria quantistica dei campi

Diagramma di Feynman Storia della teoria quantistica dei campi Background Teoria di gauge Teoria dei campi Simmetria di Poincaré Meccanica quantistica Rottura spontanea di simmetria Simmetria in fisica Crossing Coniugazione di carica Parità Simmetria T Strumenti Anomalia Teoria effettiva di campo Valore di aspettativa Ghost di Faddeev-Popov Diagramma di Feynman Formula di riduzione LSZ Funzione di partizione Propagatore Quantizzazione Rinormalizzazione Vuoto quantico Teorema di Wick Assiomi di Wightman Equazioni Equazione di Dirac Equazione di Klein-Gordon Equazione di Proca Equazione Wheeler-DeWitt Modello standard Interazione elettrodebole Meccanismo di Higgs Cromodinamica quantistica Elettrodinamica quantistica Teoria di Yang-Mills Teorie incomplete Gravità quantistica Teoria delle stringhe Supersimmetria Technicolor Teoria del tutto Scienziati Adler • Bethe • Bogoliubov • Callan • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg •Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Wilczek • Zimmermann • Zinn-Justin

Il Modello standard (MS) è una teoria fisica che descrive tre delle quattro forze fondamentali note: l'interazione forte, elettromagnetica e debole (le ultime due unificate nell'interazione elettrodebole) e tutte le particelle elementari ad esse collegate.

Ha la forma di una teoria quantistica dei campi, rinormalizzabile e coerente sia con la meccanica quantistica che con la relatività ristretta.

Le previsioni del Modello standard sono state in larga parte verificate sperimentalmente con un'ottima precisione, tuttavia esso, non comprendendo la forza gravitazionale, per la quale non esiste ad oggi una teoria quantistica coerente, non può essere considerato una teoria completa delle interazioni fondamentali.

Il modello standard non prevede inoltre l'esistenza della materia oscura, che costituisce gran parte della materia dell'universo.

Cenni storici

L'unificazione delle interazioni elettromagnetica e debole nel Modello standard è dovuta a Steven Weinberg e Abdus Salam, e precedentemente a Sheldon Glashow, che introdusse una prima formulazione basata sul gruppo di gauge SU(2)xU(1), la quale incontrava difficoltà legate all'introduzione diretta delle masse dei bosoni vettori intermedi.
Successivamente, e indipendentemente, Weinberg nel 1967 e Salam nel 1968 la estesero e completarono, integrandola con la proposta di Peter Higgs ed altri di rottura spontanea di simmetria, che permette di dare origine alle masse di tutte le particelle descritte nel modello.

Dopo la scoperta al CERN dell'esistenza delle correnti neutre deboli mediate dal bosone $Z$, come previsto dal Modello standard, Weinberg, Salam e Glashow furono insigniti del premio Nobel per la fisica nel 1979.

Il modello come proposto in origine era limitato ai soli leptoni. I quark furono introdotti successivamente grazie anche ad un lavoro pivotale del 1970 dello stesso Glashow, John Iliopoulos e Luciano Maiani, che introdussero un quarto quark, detto charm, che aveva lo scopo di sopprimere fortemente le correnti a cambiamento di stranezza (meccanismo GIM).

Le particelle elementari nel Modello standard

Schema delle interazioni tra le particelle descritte dal Modello Standard.

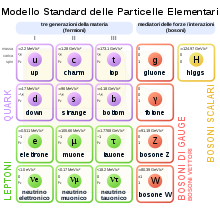
Nel Modello standard le particelle fondamentali sono raggruppate in due categorie:

• le particelle costituenti la materia, che risultano essere tutte fermioni, ovvero i quark e i leptoni. Questi ultimi comprendono i leptoni carichi e i neutrini.
• le particelle mediatrici delle forze, che risultano essere tutte bosoni, note anche come bosoni vettoriali o bosoni di gauge (i fotoni, i bosoni $W^{+}$, $W^{-}$ e $Z$ e i gluoni) in quanto la loro esistenza viene introdotta in base ad un principio di simmetria, detto appunto simmetria di gauge.

Tutta la materia ordinaria che osserviamo nel mondo macroscopico è costituita da quark e leptoni: è infatti costituita da atomi che sono a loro volta composti da un nucleo ed uno o più elettroni, che sono i più leggeri tra i leptoni carichi. Il nucleo è costituito a sua volta da protoni e neutroni che sono composti ciascuno da tre quark.

Nel Modello standard i fermioni sono raggruppati in famiglie, tre per i leptoni e tre per i quark. Le tre famiglie di leptoni comprendono ciascuna una particella carica (rispettivamente elettrone, muone e tau) ed un corrispondente neutrino. Le tre famiglie di quark prevedono ciascuna un quark di carica $+^{2}/_{3}$ ed uno di carica $-^{1}/_{3}$. I quark più leggeri sono up (u) e down (d), che combinati secondo lo schema uud formano il protone (di carica $+^{2}/_{3}+^{2}/_{3}-^{1}/_{3} = +1$), mentre combinati secondo lo schema udd formano il neutrone (di carica $+^{2}/_{3}-^{1}/_{3}-^{1}/_{3} = 0$).

I bosoni di gauge che mediano le interazioni sono: il fotone per l'interazione elettromagnetica, i due bosoni carichi W ed il bosone Z per l'interazione debole e i gluoni per l'interazione forte. Nel Modello standard è anche prevista la presenza di almeno un bosone di Higgs, la cui massa non viene prevista dal Modello e che è attualmente oggetto di ricerca da parte di alcuni grandi esperimenti, tra i quali Atlas e Compact Muon Solenoid (CMS), in fase di completamento presso l'acceleratore LHC al CERN. Il 4 Luglio 2012 è stato dato l'annuncio che i due esperimenti hanno osservato con un elevato grado di precisione (4,9 sigma per CMS e 5 sigma per Atlas) un nuovo bosone con una massa tra i 125 e i 126 GeV e con caratteristiche compatibili con il Bosone di Higgs. La scoperta è stata poi confermata ufficialmente il 6 Marzo 2013, nel corso di una conferenza tenuta dai fisici del CERN a La Thuile.

I gravitoni, cioè i bosoni che si pensa possano mediare l'interazione gravitazionale in una sua possibile formulazione quantistica, non sono considerati nel Modello standard.

L'unificazione delle forze fondamentali

Per approfondire, vedi teoria della grande unificazione.

Il Modello standard rappresenta un esempio di unificazione delle interazioni fondamentali perché le interazioni elettromagnetiche e deboli sono entrambe manifestazioni di un'unica interazione che prende il nome di forza elettrodebole. Altri esempi di unificazione sono avvenuti storicamente:

• Isaac Newton attribuì ad un'unica forza di gravità sia la caduta dei gravi che il moto dei pianeti. Questa unificazione prese il nome di gravitazione universale.
• James Clerk Maxwell, con le sue equazioni, unificò le forze elettriche e magnetiche in un'unica interazione elettromagnetica. Questa unificazione descrive le onde elettromagnetiche, che utilizziamo tutti i giorni per le nostre telecomunicazioni.

Molti fisici delle particelle ritengono che sia possibile un'unificazione delle forze ancora più profonda. L'interazione elettrodebole e quella forte, infatti, sono caratterizzate da due costanti di accoppiamento distinte nel Modello standard, ma la loro estrapolazione ad alte energie sembra indicare una possibile unificazione.

Il Modello Standard non può comprendere la gravità, la cui trattazione in relatività generale non è ad oggi compatibile con la meccanica quantistica.

Il principio di simmetria nel Modello standard

Per approfondire, vedi elettrodinamica quantistica e cromodinamica quantistica.

Alla base della formulazione del Modello standard viene posto un principio di simmetria. Questo consiste nell'invarianza della teoria sotto opportune trasformazioni, dette trasformazioni di gauge. L'invarianza di gauge garantisce la coerenza matematica e la predittività della teoria, ossia quella che tecnicamente viene definita la rinormalizzabilità della teoria.

Le trasformazioni di gauge sono relative a dei generatori: i bosoni vettori che descrivono le forze osservate in natura che sono quelle descritte dal gruppo unitario SU(3)×SU(2)×U(1). Questo gruppo è costituito dal prodotto del gruppo SU(2)×U(1) che descrive le interazioni elettromagnetiche e deboli, ed il gruppo SU(3) che descrive le interazioni forti.

La descrizione delle interazioni elettromagnetiche attraverso il gruppo U(1) prende il nome di elettrodinamica quantistica, o QED, mentre la descrizione delle interazioni forti attraverso il gruppo SU(3) prende il nome di cromodinamica quantistica, o QCD.

Le particelle che mediano le forze nelle simmetrie di gauge

Per approfondire, vedi bosoni di gauge.

Nelle teorie di gauge, ad ogni gruppo considerato corrispondono dei bosoni vettori, il cui numero dipende dal numero di generatori, che è una proprietà matematica del gruppo stesso. Al sottogruppo SU(2)×U(1) corrispondono il fotone, mediatore dell'interazione elettromagnetica, ed i bosoni W (carichi) e Z (neutro), mediatori dell'interazione debole, mentre al sottogruppo SU(3) corrispondono otto gluoni, dotati di carica di colore.

Particelle mediatrici delle forze

Forza elettromagnetica		Forza nucleare debole		Forza nucleare forte
Fotone	$\gamma$	Bosoni intermedi	$W^+$, $W^-$, $Z$	Gluone	$g$

I gluoni, a differenza dei fotoni, che hanno carica elettrica nulla, hanno la proprietà di avere carica di colore, e per questo sono a loro volta soggetti alla forza forte (questa proprietà può essere messa in relazione al fatto che SU(3) è un gruppo non abeliano). Similmente avviene per i bosoni W e Z che possono interagire tra loro. Questa proprietà è stata verificata sperimentalmente, in particolare all'acceleratore LEP, del CERN.

Le masse delle particelle ed il meccanismo di Higgs

Per approfondire, vedi bosone di Higgs.

Le teorie di gauge, di per sé, non sono in grado di descrivere bosoni vettori dotati di massa, e questo contraddirebbe quanto viene osservato sperimentalmente. Infatti, bosoni vettori massivi renderebbero la teoria non rinormalizzabile e quindi incoerente dal punto di vista fisico-matematico. Il meccanismo di rottura spontanea della simmetria del sottogruppo U(2)×U(1) è tuttavia in grado includere anche i bosoni massivi nel Modello standard, includendo nella teoria un ulteriore bosone massivo, detto bosone di Higgs. Il meccanismo di Higgs è anche in grado di spiegare, ma non prevedere quantitativamente, la massa dei fermioni.

Il 4 luglio 2012 il CERN ha annunciato che negli esperimenti Atlas e CMS dell'LHC è stata osservata, con un'attendibilità del 99,9996%, una particella compatibile con il bosone di Higgs, con massa compresa tra 125 GeV e 126 GeV .

Le tre generazioni di fermioni

I fermioni possono essere raggruppati in base alle loro proprietà di interazione in tre generazioni: la prima composta da elettroni, neutrini elettronici e dai quark up e down. Tutta la materia ordinaria è costituita, come si è visto, da elettroni e dai quark up e down. Le particelle delle due generazioni successive hanno massa maggiore delle precedenti (per quanto ne sappiamo; per i neutrini le attuali misure non permettono una misura diretta della massa, ma solo dei valori assoluti delle differenze di massa). A causa della loro maggior massa, i leptoni ed i quark della seconda e terza famiglia (o le particelle da essi costituite) possono decadere in particelle più leggere costituite da elementi della prima famiglia. Per questo, queste particelle sono instabili e presentano una breve vita media.

Organizzazione dei Fermioni

	1a generazione		2a generazione		3a generazione
Quark	Up	$u$	Charm	$c$	Top	$t$
	Down	$d$	Strange	$s$	Bottom	$b$
Leptoni	Neutrino elettronico	$\nu_e$	Neutrino muonico	$\nu_\mu$	Neutrino tauonico	$\nu_\tau$
	Elettrone	$e$	Muone	$\mu$	Tau	$\tau$

Elettrone, muone e tau e i loro corrispondenti neutrini sono classificati come leptoni.
A differenza dei quark, essi non posseggono alcuna carica di colore e quindi su di loro la forza nucleare forte non ha effetto. I quark, invece, possiedono una carica di colore, che li rende soggetti alla forza forte, che è mediata da bosoni vettori detti gluoni. I gluoni sono dotati di carica di colore e possono interagire tra di loro. Per questo motivo, e per l'elevato valore della costante di accoppiamento forte, la forza forte aumenta con l'aumentare della distanza, e fa sì che i quark non possano essere mai osservati liberi, nella materia ordinaria, ma solo combinati in stati che hanno carica di colore totale nulla.

Questi stati di colore neutro sono detti adroni, e si dividono in barioni, di tipo fermionico, composti da tre quark (come neutroni e protoni), e mesoni, di tipo bosonico, composti da una coppia quark-antiquark (come i pioni). La massa totale di tali particelle supera quella dei singoli componenti a causa dell'energia di legame.
Oltre a questi stati legati sono stati ipotizzati anche stati cosiddetti esotici costituiti da diverse combinazioni, come i pentaquark. Non esistono, tuttavia, ad oggi, evidenze sperimentali di tali stati.

Verifiche e predizioni

Il Modello standard ha predetto l'esistenza dei bosoni W e Z, del gluone, dei quark top e charm prima che tali particelle venissero osservate. Inoltre è stato sperimentalmente verificato che le caratteristiche teoriche di tali particelle sono, con buona precisione, quelle che effettivamente mostrano avere in natura.

L'acceleratore di elettroni e positroni LEP al CERN ha testato e verificato molte previsioni del Modello standard, in particolare sui decadimenti dei bosoni Z. Tra le verifiche effettuate è notevole la conferma dell'esistenza di tre famiglie di neutrini leggeri.

Sfide al Modello standard

Anche se il Modello standard ha avuto un grosso successo nello spiegare i risultati sperimentali, esso non è mai stato accettato come una teoria completa della fisica fondamentale, a causa della sua incompletezza in particolare nei seguenti punti:

1. Il modello contiene ben 19 parametri liberi, come le masse delle particelle e le costanti di accoppiamento, che devono essere determinati sperimentalmente, ma tutte queste masse non possono essere calcolate indipendentemente l'una dall'altra, quindi deve esistere fra loro una qualche relazione non prevista dal modello.
2. Il modello non può comprendere l'interazione gravitazionale.
3. Il modello non riesce a prevedere l'esistenza della materia oscura che costituirebbe gran parte della materia esistente nell'Universo.
4. Il modello standard non prevede massa per i neutrini.

Fin dal completamento del Modello standard sono stati fatti molti sforzi per superare questi limiti e trasformarlo in una teoria completa. Ad esempio la massa ai neutrini può essere aggiunta considerando anche le componenti destrorse di queste particelle. Un tentativo di superare il primo difetto è invece noto come grande unificazione: le cosiddette GUT (Grand unification theories, teorie della grande unificazione) ipotizzano che i gruppi SU(3), SU(2) e U(1) non siano altro che dei sottogruppi di un altro gruppo di simmetria ancora più grande. Ad alte energie (al di fuori dalla portata degli esperimenti condotti) la simmetria del gruppo unificatore è recuperata: a energie più basse invece si riduce a SU(3)×SU(2)×U(1) per un processo noto come rottura spontanea di simmetria.

La prima teoria di questo tipo venne proposta nel 1974 da Georgi e Glashow, con il gruppo SU(5) come gruppo di unificazione. Una proprietà distintiva di queste GUT è che, diversamente dal Modello Standard, prevedono tutte il fenomeno del decadimento protonico. Nel 1999 l'osservatorio di neutrini Super-Kamiokande ha stabilito di non aver mai osservato un decadimento protonico, stabilendo così un limite inferiore all'ipotetica emivita (tempo di dimezzamento) del protone pari a 6,7× 10³² anni. Questo ed altri esperimenti hanno invalidato, scartandole, numerose teorie GUT, fra cui quella basata sul gruppo SU(5).

Una possibile indicazione sperimentale a supporto di una unificazione delle interazioni è data dall'evoluzione delle costanti di accoppiamento dei tre gruppi SU(3), SU(2) e U(1) all'aumentare della scala di energia (tecnicamente detto running) che evolve in maniera tale che le costanti, estrapolate a grandi energie, tendono ad assumere valori vicini tra di loro. Tuttavia, la convergenza dei valori delle costanti non è esatta, cosa che fa pensare all'esistenza di ulteriori fenomeni non ancora scoperti che si manifestino tra la scala di energia della massa della Z e la scala di energia alla quale avviene la grande unificazione.

La prima conferma sperimentale della deviazione dalla formulazione originale del Modello standard venne nel 1998, quando l'esperimento Super-Kamiokande pubblicò risultati che indicavano una oscillazione dei neutrini fra tipi diversi. Questo implica che i neutrini abbiano una massa diversa da zero, dal momento che se avessero massa nulla non sarebbe possibile l'oscillazione tra sapori diversi di neutrini, oltre al fatto che dovrebbero viaggiare alla velocità della luce. Il Modello standard non prevede masse per i neutrini, che viaggiano alla velocità della luce, e presuppone soltanto l'esistenza di neutrini sinistrorsi, ovvero con spin orientato nella direzione opposta al verso del loro moto. Se i neutrini hanno una massa, allora devono per forza viaggiare più lentamente della velocità della luce ed è possibile che esistano neutrini destrosi (infatti sarebbe possibile sorpassare un neutrino, scegliendo un sistema di riferimento in cui la sua direzione di moto sia invertita senza influenzare il suo spin, rendendolo quindi destrorso). Da allora i fisici hanno rivisto il Modello Standard introducendo una massa per i neutrini, il che ha aggiunto 9 ulteriori parametri liberi (3 masse, 3 angoli di mixing e 3 fasi) oltre ai 19 iniziali; questo nuovo modello viene chiamato ancora Modello standard, nonostante le modifiche apportate.

Una ulteriore estensione del Modello standard si può trovare nella teoria della supersimmetria, che propone un compagno supersimmetrico massiccio per ogni particella del Modello standard convenzionale. La supersimmetria prevede l'esistenza di particelle stabili pesanti che hanno interazioni debolissime con la materia ordinaria. Queste particelle sono state candidate a spiegare la cosiddetta materia oscura dell'universo.

Elenco delle particelle del Modello standard

I bosoni mediatori (chiamati bosoni di gauge) presenti nel Modello standard sono:

• I fotoni, che mediano l'interazione elettromagnetica.
• I bosoni W e Z, che mediano la forza nucleare debole.
• I gluoni, in otto tipi diversi, che mediano la forza nucleare forte. Sei tipi di gluoni sono etichettati come coppie di colori e anti-colori (per esempio un gluone può portare rosso e anti-blu), mentre gli altri due sono una combinazione lineare di colore e anticolore, che formano le tre coppie rosso-antirosso, blu-antiblu e verde-antiverde.
• Il bosone di Higgs, che induce la rottura spontanea della simmetria dei gruppi di gauge ed è responsabile della massa inerziale.

I fermioni fondamentali del Modello standard, suddivisi per generazioni, sono:

Fermioni sinistrorsi nel Modello standard

1a generazione
Fermione (sinistrorso)	Simbolo	Carica elettrica	Isospin debole	Ipercarica	Carica di colore *	Massa **
Elettrone	$e^-$	$-1$	$-1/2$	$-1/2$	$\bold{1}$	511 keV
Positrone	$e^+$	$+1$	$0$	$+1$	$\bold{1}$	511 keV
neutrino elettronico	$\nu_e$	$0$	$+1/2$	$-1/2$	$\bold{1}$	< 2 eV
Quark up	$u$	$+2/3$	$+1/2$	$+1/6$	$\bold{3}$	~ 3 MeV ***
Antiquark up	$\bar{u}$	$-2/3$	$0$	$-2/3$	$\bold{\bar{3}}$	~ 3 MeV ***
Quark down	$d$	$-1/3$	$-1/2$	$+1/6$	$\bold{3}$	~ 6 MeV ***
Antiquark down	$\bar{d}$	$+1/3$	$0$	$+1/3$	$\bold{\bar{3}}$	~ 6 MeV ***
2a generazione
Fermione (sinistrorso)	Simbolo	Carica elettrica	Isospin debole	Ipercarica	Carica di colore *	Massa **
Muone	$\mu^-$	$-1$	$-1/2$	$-1/2$	$\bold{1}$	106 MeV
Antimuone	$\mu^+$	$+1$	$0$	$+1$	$\bold{1}$	106 MeV
neutrino muonico	$\nu_\mu$	$0$	$+1/2$	$-1/2$	$\bold{1}$	< 2 eV
Quark charm	$c$	$+2/3$	$+1/2$	$+1/6$	$\bold{3}$	~ 1,3 GeV
Antiquark charm	$\bar{c}$	$-2/3$	$0$	$-2/3$	$\bold{\bar{3}}$	~ 1,3 GeV
Quark strange	$s$	$-1/3$	$-1/2$	$+1/6$	$\bold{3}$	~ 100 MeV
Antiquark strange	$\bar{s}$	$+1/3$	$0$	$+1/3$	$\bold{\bar{3}}$	~ 100 MeV
3a generazione
Fermione (sinistrorso)	Simbolo	Carica elettrica	Isospin debole	Ipercarica	Carica di colore *	Massa **
Tauone (o tau)	$\tau^-$	$-1$	$-1/2$	$-1/2$	$\bold{1}$	1,78 GeV
Anti-tau	$\tau^+$	$+1$	$0$	$+1$	$\bold{1}$	1,78 GeV
neutrino Tauonico	$\nu_\tau$	$0$	$+1/2$	$-1/2$	$\bold{1}$	< 2 eV
Quark top	$t$	$+2/3$	$+1/2$	$+1/6$	$\bold{3}$	173 GeV
antiquark top	$\bar{t}$	$-2/3$	$0$	$-2/3$	$\bold{\bar{3}}$	173 GeV
Quark bottom	$b$	$-1/3$	$-1/2$	$+1/6$	$\bold{3}$	~ 4,2 GeV
antiquark bottom	$\bar{b}$	$+1/3$	$0$	$+1/3$	$\bold{\bar{3}}$	~ 4,2 GeV
Note: * - Queste cariche non sono normali cariche abeliane che possono essere sommate assieme ma autovalori delle rappresentazioni del gruppo di Lie. ** - Quella che si intende comunemente per massa nasce da un accoppiamento fra un fermione sinistrorso ed uno destrorso: per esempio, la massa di un elettrone deriva dall'accoppiamento fra un elettrone sinistrorso ed un elettrone destrorso, il quale è l'antiparticella di un positrone sinistrorso. Anche i neutrini mostrano una grande varietà nei loro accoppiamenti di massa, e per questo non è esatto parlare di masse dei neutrini nei loro tipi base o dire che un neutrino elettronico sinistrorso e un neutrino elettronico destrorso hanno la stessa massa, come questa tabella sembra suggerire. *** - Quello che in realtà è stato misurato sperimentalmente sono le masse dei barioni e degli adroni e diverse sezioni d'urto. Dal momento che i quark non si possono isolare a causa del confinamento della QCD, supponiamo che la quantità qui esposta sia la massa del quark alla scala di rinormalizzazione della transizione di fase della QCD. Per arrivare a calcolare questa quantità, i fisici devono costruire un modello su reticolo e provare ad assegnare masse diverse per i quark fino a trovare quelle per cui il modello approssima meglio i dati sperimentali. Poiché le masse dei quark di prima generazione sono molto al di sotto della scala QCD, le incertezze sono molto grandi: infatti gli attuali modelli di QCD su reticolo sembrano suggerire che le masse di questi quark siano significativamente più basse di quelle nella tabella.

Bibliografia

• (EN) G. t'Hooft. In Search of the Ultimate Building Blocks. Cambridge University Press, 2001. ISBN 978-0-521-57883-7
• (EN) W. Noel Cottingham e Derek A. Greenwood. An Introduction to the Standard Model of Particle Physics. Londra, Cambridge University Press, 1999. ISBN 978-0-521-58832-4
• (EN) F. Mandl e G. Shaw. Quantum Field Theory. ISBN 0-471-94186-7
• (EN) Y. Hayato et al.. Search for Proton Decay through p → νK⁺ in a Large Water Cherenkov Detector. Physical Review Letters 83, 1529 (1999).
• R. Oerter. La teoria del quasi tutto. Il Modello standard, il trionfo non celebrato della fisica moderna. 2006

Voci correlate

• Antimateria
• Big bang
• Bosone di Higgs
• Bosone vettore
• Bosone di gauge
• Cosmogonia
• QCD
• QED
• Elettromagnatismo
• Fisica delle particelle
• Forze fondamentali
• Gerarchia
• Modello di Kaluza-Klein
• Quark
• Supersimmetria
• Teoria della grande unificazione
• Teoria delle stringhe
• Teoria del tutto
• Teoria di gauge
• Trivialità quantistica

Altri progetti

• Commons

• Commons contiene immagini o altri file su Modello standard

Collegamenti esterni

• In SecondLife, il progetto "Scienza on the road" presenta molte discussioni sul Modello standard
• (EN) New Scientist story: Standard Model may be found incomplete
• (EN) The Universe Is A Strange Place, a lecture by Frank Wilczek
• (EN) Observation of the Top Quark at Fermilab
• Il Modello Standard, percorso in italiano - ScienzaPerTutti
• (EN) Particle Data Group

Portale Elettromagnetismo

Portale Fisica