Forza
In meccanica la forza è una grandezza fisica vettoriale in grado di mantenere o di indurre una variazione dello stato di quiete o di moto di un corpo, o di operare una sua distorsione.[1] L'interazione della forza con il corpo avviene sia a livello macroscopico, sia a quello delle particelle elementari che lo compongono. In presenza di più forze, l'effetto è determinato dalla risultante della loro composizione vettoriale.
La forza è descritta classicamente dalla seconda legge di Newton come derivata temporale della quantità di moto di un corpo rispetto al tempo.[2]
In formule:
che, nel caso la massa del corpo sia costante, si riduce a:
La legge evidenzia immediatamente il carattere vettoriale della forza, in quanto la derivata di un vettore è ancora un vettore.
Unità di misura[modifica | modifica wikitesto]
Sistema internazionale[modifica | modifica wikitesto]
L'unità di misura della forza nel SI è il newton, definito come:
Tenendo conto del secondo principio della dinamica, possiamo quindi affermare che una forza di 1 N imprime ad un corpo con la massa di 1 kg l'accelerazione di 1 m/s².
Altri sistemi di unità di misura[modifica | modifica wikitesto]
Nel sistema CGS la forza si misura in dyne.
Effetti[modifica | modifica wikitesto]
Le forze sono quindi le cause del cambiamento del moto dei corpi: possono pertanto mettere in moto un corpo che si trovava precedentemente in stato di quiete, modificare il movimento di un corpo già precedentemente in moto, o riportare il corpo in stato di quiete.
A livello pratico, le forze applicate ad un dato corpo possono avere due diversi tipi di effetti:[3]
- effetti statici: il corpo, anche se sottoposto a forze, rimane in quiete; ciò succede quando, dato uno stato iniziale di quiete, le forze subite dal corpo si bilanciano esattamente; il settore della meccanica che si occupa dello studio di questi effetti è la statica: essa analizza gli effetti delle forze sui corpi in quiete e ricerca le condizioni di equilibrio di corpi sottoposti ad un insieme di forze diverse; il più delle volte nel bilancio delle forze bisogna considerare reazioni vincolari e deformazioni dei materiali;
- effetti dinamici: inducono variazioni nella quantità di moto del corpo; la dinamica analizza appunto gli effetti delle forze sul movimento e cerca di prevedere il moto di un dato sistema di corpi se sono note le forze ad esso applicate, incluse le reazioni vincolari precedentemente citate.
Si dice ambiente di un corpo proprio l'insieme delle forze che altri corpi esercitano su di esso.

Definizione operativa di forza (punto di vista statico)[modifica | modifica wikitesto]
Da un punto di vista operativo, è possibile affermare che se un corpo è deformato rispetto al suo stato di riposo, allora è sottoposto all'azione di una forza[4].
Una definizione statica di forza è possibile misurando la deformazione di un corpo che segua la legge di Hooke, cioè tali che la deformazione sia direttamente proporzionale alla forza applicata. Ciò vuol dire che se si sospende ad una molla ideale un peso campione si ottiene un certo allungamento x, mentre se alla stessa molla si sospendono due pesi campione, uguali al precedente, l'allungamento risulta uguale a 2x. Utilizzando questa proprietà lineare delle molle è possibile costruire degli strumenti di misura delle forze, detti dinamometri.[5] Ogni volta che un dinamometro si allunga, significa che ad esso è applicata una forza.
Utilizzando un dinamometro si ottiene una misura indiretta della forza, in quanto la grandezza che viene misurata non è direttamente la forza, ma la deformazione della molla contenuta nel dinamometro; osserviamo tuttavia che la stessa situazione sperimentale ricorre nella misura della temperatura (ciò che si misura in realtà è la dilatazione del mercurio) o della pressione (viene misurata l'altezza di una colonna di liquido).
Definizione generale di forza[modifica | modifica wikitesto]
La forza generalizzata associata ad un grado di libertà del sistema i è:
Dove W è il lavoro della risultante attiva F agente sul sistema. Si tratta quindi in termini newtoniani per variabili lunghezza e angolo rispettivamente delle grandezze forza e momento meccanico prese lungo la variabile, nel caso più generale di una combinazione delle due.
Nel caso di vincoli bilaterali permettono di ignorare nell'analisi del sistema le reazioni vincolari (di risultante R), anche per sistemi scleronomi: dato uno spostamento virtuale , ottenuto considerando solo gli spostamenti ammissibili con i vincoli considerati come fissi all'istante di riferimento, il lavoro virtuale agente sull'n-esima particella del sistema vale:
Se i vincoli del sistema sono bilaterali, per il principio delle reazioni vincolari i lavori virtuali vincolari sono nulli, e cioè le reazioni sono ortogonali agli spostamenti virtuali:
Esprimendo in funzione delle coordinate generalizzate , e ricordando che per definizione di spostamento virtuale:
Il lavoro virtuale sulla particella sottoposta a vincoli bilaterali è cioè interamente calcolabile tramite le forze generalizzate agenti su di essa. A livello ingegneristico dove è necessario risalire allo sforzo che dovrebbe essere fatto da tutte le forze non vincolari se il sistema subisse uno spostamento virtuale , oppure alle sollecitazioni esterne imposte realmente dai vincoli, l'approccio Lagrangiano risulta quindi particolarmente utile.
In base alle equazioni di Lagrange del I tipo e in forma di Nielsen si può legare la forza generalizzata all'energia cinetica del sistema: , Si noti quindi che le forze generalizzate differiscono quindi per il secondo termine dalle cui si arriverebbe generalizzando la definizione newtoniana di forza come derivata totale temporale della quantità di moto, cioè il secondo principio della dinamica.
Carattere vettoriale della forza[modifica | modifica wikitesto]
La forza è una grandezza vettoriale, ovvero è descritta da un punto di vista matematico da un vettore. Ciò significa che la misura di una forza, ovvero la sua intensità misurata in newton, rappresenta solo il modulo della forza, che per essere definita necessita anche della specificazione di un punto di applicazione (il punto del corpo dove la forza agisce), di una direzione (fascio di rette parallele), della retta d'azione (la specifica retta del fascio sulla quale giace il vettore) e di un verso (indicato dall'orientamento del vettore).
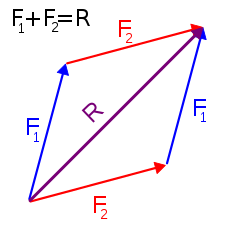
Il carattere vettoriale della forza si manifesta anche nel modo in cui è possibile sommare le forze. Come è possibile verificare sperimentalmente, due forze e con lo stesso punto di applicazione, ma direzioni diverse si sommano con la regola del parallelogramma (vedi figura a fianco). Ciò significa che se ad un corpo vengono contemporaneamente applicate le forze e , esso si muoverà lungo la direzione della diagonale del parallelogramma, come se ad esso fosse applicata solo la forza , detta, appunto somma o risultante.
Azione a distanza e campo di forze[modifica | modifica wikitesto]
Una forza può esercitarsi non necessariamente a contatto di un corpo, ma può anche esserci un campo di forze, cioè una regione in cui un corpo esercita la propria forza, esistente indipendentemente da un secondo corpo che ne subisca gli effetti.

Alcune forze possiedono una struttura tale che il lavoro compiuto su un corpo sia sempre esprimibile tramite una funzione scalare, chiamata potenziale, dipendente unicamente dagli estremi dello spostamento e non dalla traiettoria. Tali forze sono dette forze conservative e ammettono un'energia potenziale. L'energia potenziale (solitamente indicata con il simbolo U) rappresenta un campo scalare pari alla funzione potenziale cambiata di segno, di cui la forza è il gradiente:
Esempi classici di forze conservative sono la forza di gravità e la forza elettrica o di Coulomb. Esse sono caratterizzate dalle relazioni:
Il significato geometrico del gradiente di una funzione si può facilmente interpretare, almeno nel caso di funzioni in due variabili come nell'esempio in figura, come il vettore che indica, punto per punto, la massima pendenza, nella direzione crescente; il fatto che una forza conservativa sia pari a meno il gradiente dell'energia significa che è indirizzata in modo da minimizzare la stessa.
Problematicità del concetto di forza[modifica | modifica wikitesto]
La definizione operativa sopra presentata è quella più comune nei libri di testo, ma notiamo che non è soddisfacente, in quanto richiede l'introduzione della legge di Hooke e della forza peso, incappando in una definizione circolare (la definizione della legge di Hooke è dipendente dalla forza). In altre esposizioni della dinamica la forza è proprio definita dalla seconda legge della dinamica, oppure col rischio di incappare in un vero e proprio truismo. In altri trattati la forza viene introdotta come un concetto intuitivo, legato alle impressioni connesse allo sforzo muscolare: per evidenziare l'inadeguatezza di tale impostazione è sufficiente notare la pericolosità insita nella confusione tra concetti fisici appartenenti ad una teoria e concetti provenienti dall'esperienza ingenua: ad esempio mantenere sollevato un peso fermo comporta sforzo muscolare, ma non lavoro (nel senso fisico del termine).
In molte esposizioni recenti della meccanica, la forza è normalmente definita implicitamente in termini di equazioni che lavorano con essa: questa impostazione, qualora si vada a considerare la necessità di specificare il riferimento in cui tali equazioni valgono, non è completamente soddisfacente nel risolvere le problematiche associate alla definizione "classica". Alcuni fisici, filosofi e matematici, come Ernst Mach, Clifford Truesdell e Walter Noll, hanno trovato problematico questo fatto e hanno cercato una definizione più esplicita di forza, evidenziando peraltro la non essenzialità di questo concetto per la comprensione della meccanica. Ernst Mach criticò peraltro anche l'idea, a suo avviso metafisica, che le forze siano le cause del moto: solo i corpi possono influire sullo stato di moto di altri corpi e difficilmente si può pensare che la forza, un concetto astratto, possa essere la causa di alcunché.
Relazioni tra unità di forza e unità di massa[modifica | modifica wikitesto]
A livello del mare, l'accelerazione dovuta alla gravità (a nell'equazione di cui sopra) è 9,807 metri per secondo quadrato, quindi il peso di un chilogrammo è 1 kg × 9,807 m/s² = 9,807 N.
A volte, soprattutto in contesti di tipo ingegneristico, si distingue il chilogrammo massa (indicato con "kgm") per indicare il kg e il chilogrammo forza (o chilogrammo peso, indicato con "kgf") per indicare il valore di 9,807 N. Il chilogrammo peso non è tuttavia riconosciuto come unità di misura del Sistema Internazionale e sarebbe opportuno non usarlo per non creare confusione tra i concetti di massa e di peso.
Infatti la massa è una proprietà intrinseca dell'oggetto mentre il peso dipende dalla gravità.
Forze fondamentali della natura[modifica | modifica wikitesto]
Secondo le teorie scientifiche attualmente più accreditate, in natura esistono quattro forze, o meglio interazioni fondamentali che operano sui corpi: la gravità, l'interazione elettromagnetica, l'interazione nucleare forte e l'interazione debole. La prima, secondo la teoria della relatività generale è un effetto della geometria dello spazio-tempo, mentre le altre tre interazioni, che sono delle teorie di gauge, sono dovute a scambi di particelle, dette bosoni di gauge, secondo la seguente tabella:
| Forza elettromagnetica | Forza nucleare debole | Forza nucleare forte | |||
|---|---|---|---|---|---|
| Fotone | Bosoni vettori | W+, W -, Z | Gluoni | g | |
Il modello standard fornisce un riquadro coerente nel quale sono inserite le tre teorie di gauge, mentre ad oggi è stato impossibile ricondurre ad esso una versione quantistica della gravità, sebbene sia stata teorizzata una particella mediatrice (il gravitone) della quale non si hanno evidenze empiriche.
Note[modifica | modifica wikitesto]
- ^ https://www.britannica.com/science/force-physics
- ^ (EN) IUPAC Gold Book, "force"
- ^ Turchetti, p. 39.
- ^ Nota terminologica. La lingua inglese ha il solo termine strength per le parole italiane "forza" e "sforzo" che però sono distinte.
- ^ Turchetti, pp. 41-42.
Bibliografia[modifica | modifica wikitesto]
- Enrico Turchetti e Romana Fasi, Elementi di Fisica, 1ª ed., Bologna, Zanichelli, 1998, ISBN 88-08-09755-2.
Voci correlate[modifica | modifica wikitesto]
- Campo di forze
- Forza attiva
- Interazione forte
- Interazione debole
- Momento meccanico
- Dinamometro
- Newton (unità di misura)
- Dyne
- Strattone
Altri progetti[modifica | modifica wikitesto]
 Wikiquote contiene citazioni di o su forza
Wikiquote contiene citazioni di o su forza Wikizionario contiene il lemma di dizionario «forza»
Wikizionario contiene il lemma di dizionario «forza» Wikiversità contiene risorse su forza
Wikiversità contiene risorse su forza Wikimedia Commons contiene immagini o altri file su forza
Wikimedia Commons contiene immagini o altri file su forza
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) force, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | Thesaurus BNCF 8644 · LCCN (EN) sh85050452 · GND (DE) 4032651-2 · J9U (EN, HE) 987007543324305171 · NDL (EN, JA) 00926874 |
|---|