Relatività generale

La relatività generale, elaborata da Albert Einstein e pubblicata nel 1916[1], è l'attuale teoria fisica della gravitazione.
Essa descrive l'interazione gravitazionale non più come azione a distanza fra corpi massivi, come nella teoria newtoniana, ma come effetto di una legge fisica che lega la geometria (più specificamente la curvatura) dello spazio-tempo con la distribuzione e il flusso in esso di massa, energia e impulso. In particolare la geometria dello spazio-tempo identifica i sistemi di riferimento inerziali con le coordinate relative agli osservatori in caduta libera, che si muovono lungo traiettorie geodetiche. La forza peso risulta in questo modo una forza apparente osservata nei riferimenti non inerziali. La relatività generale è alla base dei moderni modelli cosmologici della struttura a grande scala dell'universo e della sua evoluzione.
Come disse lo stesso Einstein, fu il lavoro più difficile della sua carriera a causa delle difficoltà matematiche, poiché si trattava di far convergere concetti di geometria euclidea in uno spaziotempo curvo, che, in accordo con la relatività ristretta, doveva essere dotato di una struttura metrica di tipo lorentziano anziché euclideo. Egli trovò il linguaggio e gli strumenti matematici necessari nei lavori di geometria differenziale di Luigi Bianchi, Gregorio Ricci-Curbastro e Tullio Levi-Civita, che avevano approfondito nei decenni precedenti i concetti di curvatura introdotti da Carl Friedrich Gauss e Bernhard Riemann.
Storia[modifica | modifica wikitesto]
Nel 1905 Einstein risolve le contraddizioni presenti tra le equazioni di Maxwell dell'elettromagnetismo e la relatività galileiana pubblicando in un articolo la relatività ristretta. Questa nuova teoria è però a sua volta in contraddizione con la teoria della gravitazione universale di Newton e negli anni successivi Einstein cerca di modificare la teoria della gravitazione in modo da risolvere tale incompatibilità.
Dopo dieci anni di studi, nel 1915 egli propone un'equazione, oggi nota come equazione di campo di Einstein, che descrive la gravità come curvatura dello spaziotempo ed è il cuore di una teoria del tutto nuova: la relatività generale. Oltre a risolvere il conflitto con la relatività ristretta, la nuova teoria gravitazionale risulta anche più precisa di quella newtoniana nel prevedere la precessione del perielio di Mercurio.
L'equazione di campo di Einstein è una equazione differenziale alle derivate parziali non lineare, per la quale non esiste una formula risolutiva generale. Solo un anno dopo, nel 1916, l'astrofisico Karl Schwarzschild trova una particolare soluzione all'equazione, oggi nota come spaziotempo di Schwarzschild; questa soluzione è utilizzata nei decenni successivi come modello per descrivere i buchi neri.[2][3]
Nel 1919 Arthur Eddington organizza una spedizione in occasione di un'eclissi di Sole all'isola di Príncipe che verifica una delle conseguenze della teoria, la flessione dei raggi luminosi di una stella in presenza del forte campo gravitazionale del sole. Negli anni successivi Einstein si interessa alle implicazioni cosmologiche della relatività generale; per evitare l'universo dinamico (o in contrazione o in espansione) previsto dalla sua teoria e ottenere un universo statico, introduce nell'equazione di campo una nuova costante, detta costante cosmologica. Nel 1929 gli studi di Edwin Hubble mostrano però che l'universo è in espansione e il modello statico di Einstein viene abbandonato.
Le implicazioni della teoria vengono quindi studiate intensamente a partire dagli anni sessanta. Nel 1967 John Wheeler conia il termine buco nero. Una parte rilevante degli studi di fisica teorica degli ultimi decenni è dedicata a conciliare la relatività generale con la meccanica quantistica. Nel 2016 sono osservate per la prima volta le onde gravitazionali, una delle previsioni più significative della teoria.
Origini[modifica | modifica wikitesto]
Relatività ristretta e gravitazione[modifica | modifica wikitesto]

Con l'introduzione della relatività ristretta nel 1905 Einstein rende compatibili l'elettromagnetismo e la meccanica classica. Più precisamente, la teoria riesce nel difficile intento di conciliare i principi fisici seguenti:
- il principio di relatività galileiana, che asserisce che le leggi fisiche sono le stesse per tutti i sistemi inerziali. Matematicamente, ciò equivale a chiedere che tutte le leggi della fisica siano simmetriche (cioè invarianti) rispetto alle cosiddette trasformazioni galileiane;
- le equazioni di Maxwell governanti l'elettromagnetismo, e in particolare il fatto (conseguenza di queste equazioni) che le onde elettromagnetiche viaggiano sempre alla stessa velocità , indipendentemente dal sistema di riferimento scelto.
I due principi sono incompatibili. Per risolvere questa contraddizione, Einstein mantiene il principio di relatività, accetta come universale la costanza della velocità della luce introdotta dall'elettromagnetismo e sostituisce le trasformazioni galileiane con nuove trasformazioni, introdotte poco prima da Hendrik Lorentz e perciò dette trasformazioni di Lorentz. Questa modifica concettuale produce effetti concreti soltanto per corpi che viaggiano a velocità vicine a , ma cambia radicalmente le nozioni di spazio e di tempo, che, mentre nella meccanica galileiana sono distinte, nella teoria di Einstein divengono un tutt'uno nello spaziotempo (in seguito spaziotempo di Minkowski).
L'incongruenza fra le due teorie è felicemente risolta, ma la soluzione proposta crea una nuova contraddizione, questa volta con una teoria fisica vecchia di due secoli: la teoria della gravitazione universale. La teoria di Isaac Newton, infatti, è compatibile con il principio di relatività galileiana, ma non con il nuovo principio di relatività di Einstein. Le incongruenze principali sono le seguenti:
- secondo la relatività ristretta, nessuna informazione può viaggiare più veloce della luce. D'altro canto, secondo la teoria di Newton la forza di gravità ha effetto istantaneo: se il Sole si dovesse spostare in una direzione, la forza che esercita sulla Terra cambierebbe immediatamente, senza ritardo. L'informazione "il Sole si sposta" è quindi trasmessa istantaneamente, e quindi a velocità maggiori di
- la legge di gravitazione universale non è invariante rispetto alle trasformazioni di Lorentz: la forza di gravità non rispetta quindi il (nuovo) principio di relatività.
Principio di equivalenza[modifica | modifica wikitesto]

Nel 1908 Einstein enuncia un principio di equivalenza che darà successivamente un forte impulso allo sviluppo della teoria.[4] Come confermato dall' Esperienza di Eötvös e dagli esperimenti successivi, la massa inerziale e la massa gravitazionale di un corpo risultano avere lo stesso valore, cioè . Questa uguaglianza è un fatto sperimentale che non discende da alcun principio della fisica classica; i ruoli di queste due quantità sono infatti ben diversi: la massa inerziale misura quanto il corpo si opponga all'applicazione di una forza, come enunciato dal secondo principio della dinamica e cioè dalla formula
La massa gravitazionale misura invece la capacità di un corpo di attrarne un altro, di massa , secondo la legge di gravitazione universale
La massa gravitazionale ha nella legge di gravitazione universale lo stesso ruolo della carica elettrica nella legge di Coulomb.
Il fatto che queste due quantità (massa inerziale e massa gravitazionale) risultino sperimentalmente coincidere implica il fatto, osservato già da Galileo intorno al 1590, che la traiettoria di un corpo in caduta libera non dipenda dalle proprietà del corpo. Uguagliando le due formule, si ottiene infatti in particolare che la sua accelerazione è data da
I valori non dipendono infatti dalle proprietà del corpo in caduta.
Einstein studia le conseguenze della relazione formulando il seguente esperimento mentale. Si consideri un osservatore situato all'interno di una stanza chiusa. Se la stanza è poggiata sulla superficie terrestre, l'osservatore percepisce una forza verso il basso dovuta alla gravità: come mostrato in figura, lasciando cadere una palla potrà misurarne l'entità. Se la stanza è invece nello spazio, lontana da campi gravitazionali, contenuta in un razzo che sta accelerando verso l'alto, l'osservatore percepisce anche in questo caso una forza verso il basso: questa forza, dovuta all'inerzia del suo corpo, è la stessa forza che percepiamo normalmente alla partenza e all'arrivo in un ascensore. L'uguaglianza ha come conseguenza che l'osservatore non può in alcun modo capire se la forza che avverte sia dovuta a un campo gravitazionale o a un'accelerazione.
Analogamente, se la stanza è in caduta libera verso (ad esempio) la Terra, l'osservatore al suo interno non percepisce alcuna forza di gravità: se lascia cadere una moneta, osserva che questa non cade al suolo ma resta sospesa a mezz'aria. L'osservatore non ha nessuno strumento per capire se è in una zona dell'universo senza campi gravitazionali, o se invece sta cadendo verso un pianeta.
La curvatura dello spazio-tempo[modifica | modifica wikitesto]

Con la relatività ristretta, Einstein sostituisce lo spazio e il tempo newtoniano con lo spaziotempo di Minkowski. Le dimensioni sono sempre quattro, ma la novità sta nel "mescolamento" fra le tre dimensioni spaziali e quella temporale, la cui "separazione" varia a seconda del sistema in cui sta l'osservatore. Da un punto di vista matematico, lo spazio-tempo di Minkowski è dotato di un prodotto scalare lorentziano, cioè con segnatura (3,1). Non avendo lo spazio-tempo un'origine preferita, si parla più precisamente di spazio affine.
Nella relatività generale, lo spazio-tempo di Minkowski è solo un modello che approssima localmente lo spazio-tempo, che è in realtà "distorto" dalla massa. Tutte queste nozioni utilizzano concetti matematici rigorosi e non banali, sviluppati all'inizio del Novecento.
La nozione matematica che descrive uno spazio-tempo quadridimensionale localmente modellato su è quella di varietà. Le varietà sono oggetti di dimensione arbitraria abitualmente studiati in topologia. Secondo la relatività generale, lo spazio-tempo è una varietà lorentziana di dimensione 4. Il termine "lorentziano" indica che lo spazio tangente in ogni punto è dotato di un prodotto scalare di segnatura (3,1). Informalmente, questo sta a indicare che lo spazio-tempo è localmente modellato sullo spazio-tempo di Minkowski. Questo prodotto scalare di segnatura (3,1) è più precisamente un tensore, detto tensore metrico.
Come nelle varietà riemanniane, il tensore metrico governa tutta la geometria dello spazio: definisce una "distanza" fra punti e quindi una nozione di geodetica, intesa come "cammino più breve" fra due punti (queste nozioni sono un po' più sottili nel contesto lorentziano perché la distanza può essere "negativa"). La geometria locale vicino a un punto dello spazio-tempo non è però indipendente dal punto, come accade nello spazio newtoniano e in quello di Minkowski. La geometria locale qui è determinata dalla quantità di massa (e energia) presente nel punto: la massa genera curvatura, che viene misurata da alcuni strumenti matematici raffinati quali il tensore di Riemann, il tensore di Ricci e la curvatura sezionale.
Tutte queste nozioni vengono definite in modo formale: lo spazio-tempo e la sua curvatura sono descritti tramite equazioni. Da un punto di vista visivo le nostre possibilità di immaginazione sono limitate dallo spazio tridimensionale in cui viviamo: l'unico modello che riusciamo a raffigurare correttamente è quello di un universo a una dimensione spaziale (invece di tre) e una temporale. In questo caso, l'universo ha dimensione 1+1=2 e può essere raffigurato come una superficie nello spazio. Un punto materiale in movimento (o fermo) è rappresentato da una linea (detta linea di universo), che fornisce la sua posizione per ogni istante. La curvatura della superficie incide sulla traiettoria del punto in movimento in modo simile a quanto succede effettivamente nello spaziotempo. Se la superficie non contiene massa, allora è piatta e gli oggetti si muovono lungo linee rette. Se la superficie è curva, la geometria cambia e le linee di universo possono comportarsi in modo molto diverso, come accade nelle geometrie non euclidee.
Fra le complicazioni concettuali della teoria, c'è da sottolineare che la curvatura dello spazio-tempo non è solo spaziale: tutte e quattro le dimensioni sono "piegate", inclusa quella temporale (non potrebbe essere altrimenti, visto che spazio e tempo sono "mescolati" già nella versione senza massa di Minkowski).
Geodetiche[modifica | modifica wikitesto]
Ogni particella di materia si muove a velocità costante lungo una curva, chiamata geodetica, che in ogni momento (cioè localmente) può essere considerata retta. La sua velocità è data dal rapporto tra la distanza spaziale percorsa e il tempo proprio, dove il tempo proprio è quello misurato nel riferimento della particella, mentre la distanza spaziale dipende dalla metrica che definisce la struttura dello spazio-tempo.
La curvatura determina l'effettiva forma delle geodetiche e quindi il cammino che un corpo segue nel tempo. In altre parole, un corpo libero si muove nello spazio-tempo sempre lungo una geodetica, allo stesso modo in cui nella meccanica classica un corpo non sottoposto a forze si muove lungo una retta. Se la struttura dello spazio-tempo in quel punto è piatta, la geodetica sarà proprio una retta, altrimenti assumerà forme diverse, ma il corpo la seguirà comunque. In questo modo, la gravità viene a essere inglobata nella struttura dello spazio-tempo.
Ancora una volta è da notare la curvatura di cui si parla riguarda non solo le tre dimensioni spaziali, ma anche quella temporale; strutture geometriche con queste proprietà, pertanto, non possono essere visualizzate e devono essere descritte e studiate usando il linguaggio e i metodi propri della geometria differenziale.[5]
In presenza di sistemi accelerati (o, che è lo stesso, sistemi sotto l'influenza della gravità), si possono definire come inerziali solo zone locali di riferimenti e per brevi periodi. Questo corrisponde ad approssimare con una superficie piana ciò che sarebbe una superficie curva su larga scala. In tali situazioni valgono ancora le leggi di Newton.
Equazione di campo[modifica | modifica wikitesto]
«Lo spaziotempo dice alla materia come muoversi; la materia dice allo spaziotempo come curvarsi.[6]»
Matematicamente, la relatività generale descrive lo spazio-tempo come uno spazio pseudo-riemanniano[7] a 4 dimensioni; l'equazione di campo lega la curvatura in un punto dello spazio-tempo al tensore energia impulso che descrive la densità e il flusso di materia e di energia in . La forma esplicita dell'equazione di campo è:
Tutti i membri dell'equazione sono tensori simmetrici di dimensione 4x4, contenenti quindi 10 componenti indipendenti che variano con il punto . Brevemente, il membro a sinistra dell'uguaglianza misura la curvatura e la geometria dello spazio-tempo in , mentre quello di destra misura la densità e il flusso di materia e energia in . L'equazione descrive quindi in che modo la materia "piega" lo spazio-tempo e ne determina la geometria.
Più precisamente, le variabili presenti nell'equazione sono le seguenti:
- è il tensore di curvatura di Ricci,
- è la curvatura scalare,
- è il tensore metrico,
- è la costante cosmologica,
- è il tensore energia impulso
- è la velocità della luce nel vuoto,
- è la costante gravitazionale.
Il tensore metrico descrive completamente la metrica dello spazio-tempo: l'equazione di campo va quindi interpretata come una equazione differenziale con incognita . La curvatura scalare è la traccia del tensore di curvatura di Ricci uguale a . Il tensore di Ricci e la curvatura scalare misurano la curvatura dello spazio-tempo e dipendono dal tensore metrico e dalle sue derivate parziali prime e seconde: si tratta quindi di una equazione al secondo ordine.
Il tensore metrico ha 10 componenti indipendenti, ma i gradi di libertà di questo sistema sono in numero minore. Si deve infatti tenere conto delle identità di Bianchi e della libertà di gauge della teoria: è possibile effettuare una trasformazione qualunque sulle quattro coordinate, il che porta a sei le componenti del tensore metrico effettivamente indipendenti. Le quattro identità di Bianchi, che implicano la conservazione del tensore di Einstein, riducono ulteriormente le componenti libere del campo gravitazionale a due, lo stesso numero dei gradi di libertà del campo elettromagnetico.[8]
L'equazione di campo derivata da Einstein è l'unica possibile di secondo ordine nelle derivate e che rispetta la co-varianza generale; accoppiamenti non-minimali alla materia possono essere inclusi nella definizione del tensore energia-impulso.
Tale equazione contiene un termine numerico Λ, chiamato costante cosmologica, che Einstein introdusse con valore negativo per permettere un universo statico. Nella decina di anni successiva, osservazioni di Hubble mostrarono che l'universo è in espansione e il termine cosmologico venne rimosso dalle equazioni (lo stesso Einstein giudicò la sua introduzione l'errore più grave da lui commesso nella vita). L'idea di Einstein di introdurre la costante cosmologica venne però riconsiderata nella seconda metà del XX secolo, non più per garantire un universo statico ma per spiegare l'espansione accelerata dell'universo. Nel 1998, l'osservazione dello spostamento verso il rosso di supernove lontane, ha costretto gli astronomi a impiegare una costante cosmologica positiva per spiegare l'accelerazione dell'espansione dell'Universo.
Soluzioni[modifica | modifica wikitesto]
Le soluzioni dell'equazione di campo dipendono dal sistema che si sta considerando. Possono inoltre distinguersi in soluzioni locali o globali.
Le soluzioni locali, in cui si considera per esempio una massa posta nell'origine del sistema di riferimento, presuppongono una metrica che descriva uno spazio-tempo piatto per grandi distanze dall'origine. Queste soluzioni si dividono a seconda dei valori assunti dai parametri m (massa), a (momento angolare), Q (carica elettrica), tutte quantità espresse con la convenzione semplificativa . Ovviamente nel caso Q sia non nulla, oltre all'equazione di campo di Einstein, si dovranno risolvere simultaneamente le equazioni di Maxwell del campo elettro-magnetico. Inoltre si distinguono soluzioni nel vuoto quando è nullo, o nella materia quando è non nullo (per materia si intende sia massa sia energia).
Le soluzioni più conosciute utilizzate in cosmologia sono
Vi sono poi quelle utilizzate per lo studio teorico dei buchi neri, derivate ponendo e :
- m≠0, a=0, Q=0 (corpo dotato di massa, non rotante, scarico): metrica di Schwarzschild.
- m≠0, a≠0, Q=0 (corpo dotato di massa, rotante, scarico): metrica di Kerr.
- m≠0, a=0, Q≠0 (corpo dotato di massa, non rotante, carico): metrica di Reissner-Nordström.
- m≠0, a≠0, Q≠0 (corpo dotato di massa, rotante, carico): metrica di Kerr-Newmann.
Dal precedente prospetto si può vedere come, una volta ricavata la metrica (ovvero il ) di Kerr-Newmann, si possano ricavare tutte le altre per semplificazione, ponendo di volta in volta i vari parametri a zero.
Metrica di Kerr-Newman[modifica | modifica wikitesto]
La metrica di Kerr-Newman è dunque con m≠0, a≠0 e Q≠0, ed è quindi a simmetria assiale:
dove
raccogliendo i termini con i differenziali simili
si può scrivere la matrice che rappresenta il tensore metrico
Metrica di Kerr[modifica | modifica wikitesto]
Annullando Q nella metrica di Kerr-Newmann si ottiene la metrica di Kerr, soluzione dell'equazione di campo (senza campo elettromagnetico), anch'essa a simmetria assiale:
dove ora
Operando lo stesso tipo di raccoglimento che per la metrica di Kerr-Newmann, si può scrivere la rappresentazione matriciale del tensore metrico
Metrica di Reissner-Nordström[modifica | modifica wikitesto]
Se nella metrica di Kerr-Newmann, invece della carica elettrica Q, si annullasse il momento angolare a, si otterrebbe la metrica di Reissner-Nordström, a simmetria sferica:
dove
e la rappresentazione matriciale è
Metrica di Schwarzschild[modifica | modifica wikitesto]
Se infine si pongono a=0 e Q=0 si ottiene la metrica di Schwarzschild, soluzione delle equazioni di Einstein (senza campo elettro-magnetico) in simmetria sferica. Si avrà quindi
sapendo che ora
e in forma matriciale si avrà
La metrica è singolare nei punti ove è singolare la matrice (in tal caso si estende il concetto di singolarità per comprendere anche ). Per la metrica di Schwarzschild ciò avviene quando
Nel primo caso si ha una singolarità eliminabile cambiando coordinate (passando ad esempio alle coordinate di Kruskal). Il valore è noto come raggio di Schwarzschild (ovvero la distanza dal centro del buco nero a cui si forma l'orizzonte degli eventi). Il fatto che tale singolarità sia dovuta solo a una cattiva scelta delle coordinate è verificato facilmente sapendo ad esempio che lo scalare di curvatura non è ivi divergente, o notando che le geodetiche possono essere prolungate attraverso l'orizzonte degli eventi. Nel secondo caso, viceversa, si tratta di una singolarità non eliminabile e corrisponde a una curvatura infinita dello spazio-tempo (lo scalare di curvatura è divergente), spesso raffigurata come un imbuto senza fine, una smagliatura nel tessuto spaziotemporale.
Conferme sperimentali[modifica | modifica wikitesto]

Poiché le equazioni della relatività generale hanno come variabile di campo la metrica dello spazio-tempo, non è facile ricavarne effetti osservabili. In condizioni di campo gravitazionale debole, le previsioni della teoria in termini di "forza di gravità" sono pressoché indistinguibili da quelle della gravitazione newtoniana; d'altra parte, non è possibile creare in laboratorio campi gravitazionali intensi, quindi le verifiche della teoria possono essere osservative (attraverso misure astronomiche), ma non sperimentali. Inoltre la misura diretta della curvatura dello spazio-tempo (intensità del campo gravitazionale) non è possibile, e gli effetti della relatività generale sulle misure di distanze spaziali e intervalli temporali da parte di un osservatore sono tuttora oggetto di attiva ricerca teorica[9]. A tutt'oggi vengono proposti esperimenti per la conferma o meno di tale teoria, che al momento attuale ha sempre resistito agli attacchi. Sono indicati qui sotto solo i più importanti.
La prima conferma (ancorché incompleta, come è emerso in seguito) si ebbe nel 1919, quando osservazioni di Arthur Eddington durante un'eclissi di Sole confermarono la visibilità di alcune stelle vicine al bordo solare, che in realtà sarebbero dovute essere invisibili: i fotoni luminosi venivano deviati dal Sole della quantità prevista dalle equazioni. In realtà, le osservazioni avevano un errore medio dello stesso ordine di grandezza dell'effetto considerato. La prima vera conferma fu la spiegazione del moto di precessione del perielio di Mercurio, la cui entità era inspiegabile con la gravitazione newtoniana (anche tenendo conto dell'effetto perturbativo dovuto all'attrazione degli altri pianeti), e invece coincideva con quanto previsto dalla relatività generale.
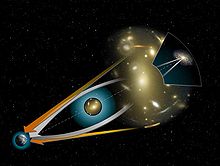
Un'altra conferma più recente, ormai completamente accettata dalla comunità scientifica, è l'effetto lente gravitazionale di cui le osservazioni di Eddington sono un caso particolare. La luce emessa da una sorgente lontana, transitando nelle vicinanze di un oggetto molto massiccio può venire deviata, con un effetto complessivo che può sdoppiare (o meglio trasformare in un anello), l'immagine della sorgente.
È relativamente recente la scoperta indiretta dell'esistenza dei buchi neri, oggetti pesanti e compatti, dalla cui superficie non può sfuggire (quasi) nulla, essendo la velocità di fuga superiore a quella della luce. Quasi nulla in quanto il fisico Stephen Hawking ha dimostrato come i buchi neri evaporino perdendo particelle, per lo più fotoni, (radiazione di Hawking) tanto più velocemente quanto più piccola è la massa del buco nero. Questo risultato deriva direttamente dalla conservazione del secondo principio della termodinamica, ed è stata la prima applicazione congiunta di relatività generale e meccanica quantistica. Questo risultato contraddice, però, la meccanica quantistica stessa, in quanto la radiazione di Hawking contiene molta meno informazione della materia entrante nel buco nero. Ciò porta a una perdita di informazione, contravvenendo a uno dei principi fondamentali della quantistica. Questa contraddizione ha fatto sì che taluni scienziati contemporanei abbiano negato l'esistenza dei buchi neri a favore di nuove teorie.
Sono state rilevate nel 2016 alcune onde gravitazionali, originate dalla collisione di due buchi neri molto massivi. Queste onde erano state previste dalla teoria relativistica ma solo 100 anni dopo ne è stata confermata l'esistenza.
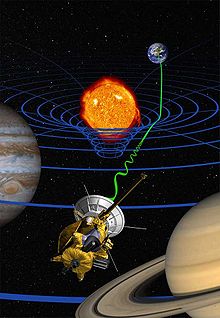
Un altro risultato che confermerebbe la teoria è il cosiddetto frame dragging, ossia il trascinamento del sistema di riferimento da parte di masse in rotazione: oltre alla sonda Gravity Probe B della NASA, un articolo di un ricercatore dell'Università di Bari ha utilizzato i dati dell'orbita del satellite Mars Global Surveyor (MGS), confermando entro l'errore di meno dell'1% le previsioni della teoria (Iorio 2007).
Inoltre sarebbe una conferma alla relatività einsteiniana la giusta correzione della posizione calcolata dai GPS. Infatti da una parte c'è l'effetto di ritardo dovuto all'elevata velocità dei satelliti circa 14000 km/h (per la Relatività Ristretta, ritardo di circa 6 microsecondi al giorno). Inoltre sono anche soggetti all'azione della relatività generale, ovvero alla gravità e questo comporta una differenza nei tempi di comunicazione di circa 45 microsecondo di anticipo. Totale correzione: anticipo di 39 microsecondi al giorno (45 di anticipo meno 6 di ritardo).
Campo di validità della relatività[modifica | modifica wikitesto]
Come risulta dagli articoli di Einstein, le leggi della relatività descrivono trasformazioni reversibili e vengono utilizzate per onde e particelle che si muovono nello spazio vuoto. Contemporaneamente, Einstein ha pubblicato anche le versioni corrette di idrodinamica, meccanica e magnetismo.
La relatività generale è stata formulata solo come teoria classica, ossia non quantistica. Trasformarla in una teoria quantistica di campo con le tecniche usuali della seconda quantizzazione si è rivelato impossibile (la teoria non è rinormalizzabile). D'altra parte, non si è neppure finora ottenuta una formulazione completamente consistente della meccanica quantistica, né della teoria quantistica dei campi, su spazi-tempi curvi.
Questo determina problemi teorici non facilmente risolubili ogni qualvolta si cerchi di descrivere l'interazione fra il campo gravitazionale e le particelle subatomiche. Carlo Rovelli ha sostenuto al riguardo che la relatività generale e la meccanica quantistica «non possono essere entrambe giuste, almeno nella loro forma attuale, perché si contraddicono l'un l'altra»:[10] per la prima infatti «il mondo è uno spazio curvo dove tutto è continuo», per la seconda invece «il mondo è uno spazio piatto dove saltano quanti di energia».[11]
Difficoltà analoghe emergono in cosmologia, allorché si deve ricostruire il comportamento di spazio, tempo e materia in condizioni di grande densità di massa-energia, come nell'universo primordiale o in presenza di singolarità dello spazio-tempo (buchi neri). La costruzione di una teoria quantistica della gravitazione, eventualmente come uno degli aspetti di una teoria unificata più generale, è uno degli obiettivi più importanti per la fisica del XXI secolo.
Note[modifica | modifica wikitesto]
- ^ (DE) Die Grundlage der allgemeinen Relativitätstheorie (Articolo originale della teoria della relatività generale) (PDF), su myweb.rz.uni-augsburg.de, 1916. URL consultato il 19 marzo 2018.
- ^ Karl Schwarzschild, Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie, in Sitzungsber. Preuss. Akad. D. Wiss., 1916a, pp. 189–196.
- ^ Karl Schwarzschild, Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie, in Sitzungsber. Preuss. Akad. D. Wiss., 1916b, pp. 424–434.
- ^ Albert Einstein, Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen (PDF), in Jahrbuch der Radioaktivitaet und Elektronik, vol. 4, 1907, p. 411. URL consultato il 5 maggio 2008.
- ^ Solo a fini divulgativi si può cercare di esemplificare il concetto di curvatura di uno spazio riemanniano utilizzando superfici curve bidimensionali (come nella nota immagine del telo elastico incurvato dal peso di un corpo massivo): queste tuttavia non esibiscono tutti i fenomeni che possono presentarsi in dimensione tre e quattro, tanto più che noi riusciamo a visualizzare superfici immerse in uno spazio tridimensionale euclideo, non pseudoeuclideo.
- ^ Jim Baggott, Origini. La storia scientifica della creazione, Adelphi, 2015 (Capitolo 1: "In principio", sezione: "Massa ed energia").
- ^ Si definisce spazio riemanniano una varietà differenziabile dotata di un tensore metrico definito positivo (euclideo), e spazio pseudo-riemanniano una varietà differenziabile dotata di tensore metrico di segnatura indefinita, detto anche metrica pseudo-euclidea
- ^ Il gravitone, una ipotetica particella mediatrice della interazione gravitazione, avrebbe perciò elicità due.
- ^ L. Lusanna, The Chrono-geometrical Structure of Special and General Relativity, Lectures given at the 42nd Karpacz Winter School of Theoretical Physics, Ladek, Poland, 6-11 February 2006 [1]
- ^ Carlo Rovelli, Sette brevi lezioni di fisica, Milano, Adelphi, 2014, p. 47.
- ^ C. Rovelli, ibidem, p. 51.
Bibliografia[modifica | modifica wikitesto]
- Hermann Bondi, La relatività e il senso comune, Bologna, Zanichelli, 1963
- (EN) Sean M. Carroll, Spacetime and Geometry: An introduction to General Relativity. Spacetime and Geometry, Addison-Wesley, 2004. ISBN 0-8053-8732-3
- Rodolfo Damiani, La Relatività, lo spirituale nella scienza, Barzago, Marna, 2005. ISBN 88-7203-295-4
- Arthur Stanley Eddington, Spazio, tempo e gravitazione: la teoria della relatività generale, Torino, Bollati Boringhieri, 2003. ISBN 88-339-0287-0
- Albert Einstein, Come io vedo il mondo. La teoria della relatività, Collana Grandi Tascabili Newton Compton, Bologna, Newton Compton Editore, 1975
- Wolfgang Pauli, Teoria della relatività, Torino, Bollati Boringhieri, 2008. ISBN 978-88-339-1864-8
- Tullio Regge, Spazio, tempo e universo: passato, presente e futuro della teoria della relatività, Torino, Utet, 2005. ISBN 88-7750-945-7
- Bertrand Russell, L'ABC della relatività, prefazione di Piergiorgio Odifreddi, Milano, Tea, 2008. ISBN 978-88-502-0648-3
- (EN) Bernard F. Schutz, A First Course in General Relativity, Cambridge University Press, 1985. ISBN 0-521-27703-5
- (EN) John Stewart, Advanced General Relativity, Cambridge University Press, 1993. ISBN 0-521-44946-4
- (EN) Kip S. Thorne, Charles W. Misner, John A. Wheeler, Gravitation, San Francisco, W. H. Freeman, 1973. ISBN 0-7167-0344-0
- (EN) Robert M. Wald, General Relativity (1984), University of Chicago Press. ISBN 0-226-87033-2
- (EN) Steven Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, J. Wiley, 1972. ISBN 0-471-92567-5
- (EN) Clifford M. Will, Theory and Experiment in Gravitational Physics, Cambridge University Press, 1993. ISBN 0-521-43973-6
- Approfondimenti
- (DE) Max Born, Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen, Berlin, Springer, 1920.
- (EN) Max Born, Einstein's theory of relativity [Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen], New York, Dutton, 1922.
Voci correlate[modifica | modifica wikitesto]
- Cono di luce
- Diagramma di Penrose
- Albert Einstein
- Equazione di campo di Einstein
- Equazioni di Friedmann
- Lente gravitazionale
- Approssimazione per i campi gravitazionali deboli
- Problema di Keplero nella relatività generale
- Singolarità gravitazionale
- Gravità quantistica
- Relatività ristretta
- Relatività. Esposizione divulgativa
- Società italiana di relatività generale e fisica della gravitazione
Altri progetti[modifica | modifica wikitesto]
 Wikisource contiene una pagina sulla relatività generale
Wikisource contiene una pagina sulla relatività generale Wikimedia Commons contiene immagini o altri file sulla relatività generale
Wikimedia Commons contiene immagini o altri file sulla relatività generale
Collegamenti esterni[modifica | modifica wikitesto]
- Un'altra conferma per la relatività generale, su lescienze.espresso.repubblica.it.
- (EN) Soluzione per le equazioni di campo di Felber, su physorg.com.
- (EN) Articolo approfondito su arXiv, su arxiv.org.
- (EN) Sorgente dell'articolo con alcuni filmati avi nell'archivio tar.gz (cliccare su Download source)
- (EN) Barrow, J. e Sherrer, R., Bosoni e fermioni producono lo stesso campo gravitazionale?
- (EN) New Scientist press release of the MGS test by Iorio in the gravitational field of Mars, su space.newscientist.com. URL consultato il 21 gennaio 2007 (archiviato dall'url originale il 15 marzo 2008).
| Controllo di autorità | Thesaurus BNCF 68305 · LCCN (EN) sh85053765 · GND (DE) 4112491-1 · BNF (FR) cb119326985 (data) · J9U (EN, HE) 987007562795805171 |
|---|

























![{\displaystyle ds^{2}=-\Sigma \Delta ^{-1}dr^{2}-\Sigma d\vartheta ^{2}-\Sigma ^{-1}\operatorname {sen} ^{2}\vartheta [adt-(r^{2}+a^{2})d\varphi ]^{2}+\Sigma ^{-1}\Delta [dt-a\,\operatorname {sen} ^{2}\vartheta d\varphi ]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a050ae2e3608eb7ed62def1b3d5ee04ffec2bd26)



![{\displaystyle +\Sigma ^{-1}[\Delta -a^{2}\,\operatorname {sen} ^{2}\vartheta ]dt^{2}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c11ff1a27a3357131deecde003d7d3c625b1cf81)


![{\displaystyle -\Sigma ^{-1}\operatorname {sen} ^{2}\vartheta [(r^{2}+a^{2})^{2}-a^{2}\Delta \operatorname {sen} ^{2}\theta ]d\varphi ^{2}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df200f161882df298c262cefebfd14b1ba55275f)

![{\displaystyle g_{ik}=\left({\begin{matrix}+\Sigma ^{-1}[\Delta -a^{2}\operatorname {sen} ^{2}\vartheta ]&0&0&+a\Sigma ^{-1}\operatorname {sen} ^{2}\vartheta (2Mr-Q^{2})\\0&-\Sigma \Delta ^{-1}&0&0\\0&0&-\Sigma &0\\+a\Sigma ^{-1}\operatorname {sen} ^{2}\vartheta (2Mr-Q^{2})&0&0&-\Sigma ^{-1}\operatorname {sen} ^{2}\vartheta [(r^{2}+a^{2})^{2}-a^{2}\Delta \operatorname {sen} ^{2}\theta ]\end{matrix}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d699c124dc8ced7ca00e3a24e4f0618ad1ca3bf4)


![{\displaystyle g_{ik}={\begin{pmatrix}+1-2\Sigma ^{-1}Mr&0&0&+2a\Sigma ^{-1}Mr\operatorname {sen} ^{2}\vartheta \\0&-\Sigma \Gamma ^{-1}&0&0\\0&0&-\Sigma ^{2}&0\\+2a\Sigma ^{-1}Mr\,\operatorname {sen} ^{2}\vartheta &0&0&-\operatorname {sen} ^{2}\vartheta [(r^{2}+a^{2})+2\Sigma ^{-1}Mra]\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ed4f03087d348c6d769b2fcc44bf28fa5a2c7cc)











