Geodetica
In matematica, e più precisamente in geometria differenziale, una geodetica è la curva più breve che congiunge due punti di uno spazio. Lo spazio in questione può essere una superficie, una più generale varietà riemanniana, o un ancor più generale spazio metrico. Ad esempio, nel piano le geodetiche sono le linee rette, su una sfera sono gli archi di cerchio massimo. Il concetto di geodetica è intimamente correlato a quello di metrica riemanniana, che è connesso con il concetto di distanza.
In matematica, le geodetiche hanno un ruolo fondamentale nello studio delle superfici (ad esempio, quella terrestre), e delle varietà astratte aventi dimensione 3 o maggiore. Sono importanti per descrivere alcune geometrie non euclidee, come la geometria iperbolica.
In fisica, le geodetiche ricoprono un ruolo importante nello studio dei moti dei corpi in presenza di campi gravitazionali, dal momento che la relatività generale interpreta la forza gravitazionale come una deformazione dello spazio-tempo quadridimensionale.
Introduzione[modifica | modifica wikitesto]
Superfici e varietà[modifica | modifica wikitesto]

Il termine "geodetica" deriva da geodesia, la scienza della misurazione delle dimensioni e della forma del globo terrestre; nel suo significato originale, una geodetica era il cammino più breve tra due punti sulla superficie della Terra, ossia un arco di cerchio massimo. Gli archi di meridiani e di equatore sono geodetiche, mentre gli altri paralleli no.
In matematica, una geodetica è ancora una curva che descrive (almeno localmente) il cammino più breve su un dato spazio. Lo spazio in esame può essere una superficie contenuta nello spazio tridimensionale, o una più generale varietà riemanniana, ovvero uno "spazio curvo" astratto di dimensione arbitraria.
Relatività generale[modifica | modifica wikitesto]

Le geodetiche hanno assunto un significato fisico importante all'inizio del XX secolo, per il loro ruolo nella relatività generale. Secondo la relatività, lo spaziotempo è infatti uno spazio "curvo" di dimensione 4, in cui le geodetiche descrivono la traiettoria di un punto materiale in presenza di un campo gravitazionale. Sono quindi geodetiche le traiettorie di un sasso che cade, di un satellite in orbita e persino di un raggio di luce.
La curvatura dello spaziotempo è causata dalla presenza di massa, come suggerito in figura. La traiettoria di un raggio di luce, come quella di qualsiasi oggetto, è quindi determinata dalla distribuzione della massa nello spazio. La relazione precisa fra massa e curvatura è espressa dalla equazione di campo di Einstein.
Geometrie non euclidee[modifica | modifica wikitesto]

Una geodetica è completa se si estende indefinitamente in entrambe le direzioni. Le geodetiche del piano euclideo sono quindi le rette, di lunghezza infinita in ambo le direzioni.
Le geodetiche su un più generale spazio soddisfano spesso tutti i postulati di Euclide richiesti per le rette nel piano, eccetto il V postulato, riguardante le rette parallele. In questo modo è quindi possibile costruire numerose geometrie non euclidee, con comportamenti qualitativamente molto differenti fra loro.
Il V postulato dice che per ogni retta e ogni punto non contenuto in questa, esiste esattamente una retta passante per il punto parallela alla prima. Lo stesso enunciato espresso per le geodetiche (dove "parallele" vuol dire "che non si intersecano") è infatti falso in molti casi. Ad esempio, non esistono geodetiche parallele nella sfera (due cerchi massimi si incontrano sempre), mentre se ne trovano infinite nello spazio iperbolico.
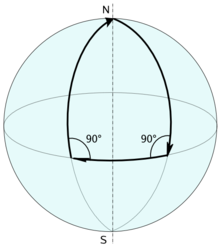
In uno spazio non euclideo, molti dei teoremi della geometria piana non sono più validi. Ad esempio, la somma degli angoli interni di un triangolo, i cui lati sono 3 geodetiche, può essere diversa da . Ad esempio, sulla sfera questa somma è sempre superiore a .
Spazio metrico[modifica | modifica wikitesto]
Definizione[modifica | modifica wikitesto]
Su un generale spazio metrico , una geodetica è una curva
definita su un intervallo della retta reale , che realizzi localmente la distanza fra punti. Più precisamente, ogni punto dell'intervallo ha un intorno in tale che per ogni coppia e di punti in vale l'uguaglianza
Se questa uguaglianza è valida per ogni coppia di punti e in , la geodetica è minimizzante: in questo caso la geodetica realizza la minima distanza non solo localmente, ma globalmente.
Generalmente, nella definizione di geodetica, si ammette nell'uguaglianza la presenza di una costante moltiplicativa al secondo membro, in analogia con la definizione data per le varietà riemanniane. Questa costante può però essere sempre ridotta a uno dopo aver riparametrizzato la curva secondo la sua lunghezza d'arco.
Una geodetica chiusa è una curva
definita sulla circonferenza , che è una geodetica se ristretta a qualsiasi arco contenuto in .
Esempi[modifica | modifica wikitesto]
Le geodetiche nello spazio euclideo sono i segmenti, cioè le porzioni di rette. Sono tutte del tipo
dove e sono due vettori dello spazio. Questa rappresentazione è parametrizzata secondo la lunghezza d'arco se e solo se .
Varietà (pseudo)-riemanniana[modifica | modifica wikitesto]
Una varietà riemanniana o pseudoriemanniana è in particolare uno spazio metrico, e quindi la nozione di geodetica è definita[1].
Minimizzare lunghezza o energia[modifica | modifica wikitesto]
La traiettoria più breve tra due punti su di uno spazio curvo può essere trovata scrivendo l'equazione della lunghezza di una curva, e minimizzando poi tale lunghezza tramite tecniche standard del calcolo delle variazioni.
La lunghezza di una curva
su una varietà riemanniana è data dall'equazione
La geodetica risulta essere una curva che, all'interno dello spazio di tutte le curve aventi estremi fissati, è punto di minimo, o più generalmente un punto stazionario, per la funzione "lunghezza"
Il concetto di "punto stazionario" deve però essere espresso con cautela, perché lo "spazio di tutte le curve" è un oggetto abbastanza complesso, avente intrinsecamente dimensione infinita. A questo scopo viene in aiuto il calcolo delle variazioni.
Equivalentemente, si può utilizzare un'altra quantità, detta l'energia della curva:
I due concetti portano allo stesso risultato: le geodetiche sono punti stazionari sia per la lunghezza che per l'energia. Intuitivamente, ciò può essere compreso dal fatto che un elastico teso fra due punti contrae la propria lunghezza, e così facendo minimizza anche la propria energia potenziale; la forma risultante dell'elastico è comunque una geodetica.
Esistenza e unicità di geodetiche[modifica | modifica wikitesto]
Per ogni punto di una varietà riemanniana , e per ogni vettore non nullo dello spazio tangente in , esiste esattamente una geodetica completa passante per e tangente a .
Esistono cioè e una geodetica
con e , tale che ogni altra geodetica con queste ultime due proprietà è la stessa definita su un sotto-intervallo di . I valori e possono anche essere infiniti.
L'esistenza e unicità derivano dal fatto che una geodetica è soluzione di un particolare problema di Cauchy del secondo ordine.
Se il vettore è moltiplicato per uno scalare, la geodetica corrispondente è anch'essa riscalata (e invertita, se lo scalare è negativo). Si può quindi dire che, come nella geometria piana, per ogni punto e per ogni direzione esiste un'unica geodetica completa passante per il punto e orientata lungo quella data direzione. Secondo questa linea, viene definita la mappa esponenziale.
Completezza[modifica | modifica wikitesto]
Per il teorema di Hopf-Rinow, una varietà riemanniana è completa se e solo se ogni geodetica può essere prolungata indefinitamente in entrambe le direzioni. In questo caso, i valori e ricavati nella sezione precedente sono sempre infiniti.
La geodetica e la relatività generale[modifica | modifica wikitesto]
N.b.: di seguito vengono utilizzate le coordinate . La segnatura della metrica piatta è .
Nel suo libro "La teoria della relatività", Albert Einstein, il primo scienziato ad aver utilizzato le geodetiche in fisica, dà la seguente definizione:
- .
Essa rappresenta una linea (non un'area) tracciata fra due punti e del continuo quadridimensionale (tre dimensioni dello spazio e una del tempo).
Le curve che passano per detti punti sono infinitamente vicine alla geodetica. Esprimendole in forma parametrica e con altre 2 pagine circa di passaggi, Einstein deduce l'equazione della geodetica:
- .
Secondo la relatività ristretta, un corpo non soggetto a forze esterne si muove di moto traslatorio rettilineo uniforme. Ciò è anche il principio di relatività galileiana, cui Einstein aggiunse un'informazione: è valido soltanto in assenza di campo gravitazionale (ciò che caratterizza le regioni dello spazio-tempo in cui vale la relatività ristretta).
In un sistema di riferimento collocato in una regione dello spazio-tempo in cui vale la relatività ristretta (in assenza di campo gravitazionale), l'equazione che descrive un moto rettilineo uniforme è una geodetica.
Poiché la geodetica è definita indipendentemente dal sistema di coordinate, e quindi anche l'equazione della geodetica, tale legge vale per un sistema di riferimento arbitrario. Per generalizzare, abbiamo dovuto anticipare che relatività ristretta significa assenza di campo gravitazionale. L'equazione del moto del punto materiale diventa:
- .[2]
Imporre che il generico simbolo di Christoffel, un ente matematico, sia collegato all'intensità del campo gravitazionale, è un'interpretazione fisica, che Einstein basa su un esperimento mentale e un ragionamento discorsivo ma che si dimostra rigorosamente.
Bisogna ricordare che l'elemento lineare (v.relatività generale) misura qualsiasi variazione nello spazio e nel tempo. Se è una generica coordinata, il fatto che la derivata seconda rispetto all'elemento lineare è nulla significa che il corpo si muove nello spazio e nel tempo secondo incrementi costanti, che né crescono né diminuiscono.
L'annullamento della derivata seconda significa che il moto non subisce variazioni nello spazio (è rettilineo) e nel tempo (uniforme). Questo avviene nelle regioni di spazio tempo in cui le componenti gravitazionali sono nulle, ovvero
- .
Bisogna notare che la componente temporale ha segno opposto rispetto alle componenti spaziali, come detto in commento all'equazione per misurare il .
Einstein commenta a proposito: «le componenti del campo gravitazionale sono le quantità che caratterizzano lo scostamento del moto rettilineo uniforme». Non bisogna confondere la presenza di una forza gravitazionale (possibile anche in un moto rettilineo) dall'azione di un campo gravitazionale, che richiede una variazione di questa forza. L'equazione contiene le derivate prime delle componenti della gravità.
Mediante una semplice «sostituzione comunque scelta», lo stesso moto del punto materiale libero, osservato da un altro sistema di riferimento, diviene curvilineo non uniforme, con una legge non più dipendente dalla natura fisica del punto materiale che si muove. La legge del moto (rettilineo uniforme quando le componenti sono costanti) cambia radicalmente nelle nuove coordinate. Il moto rettilineo uniforme dipendente dalle proprietà della massa, diviene un moto curvilineo non uniforme indipendente dalle proprietà fisiche dell'oggetto in movimento. Nel caso più generale, quindi, il punto in movimento può essere trattato come una generica massa, in quanto il moto non dipende dal materiale di cui il corpo è fatto, o da altre proprietà chimiche.
L'effetto di un nuovo campo gravitazionale e di un semplice cambio di coordinate, matematicamente sono gli stessi: la distorsione del moto uniforme è visibile all'osservatore e misurabile in entrambi i casi, sebbene nel secondo non ci sia alcuna variazione né del corpo né delle forze a cui è soggetto. Il cambio di coordinate, sebbene muti radicalmente le leggi del moto, porta egualmente a delle conclusioni coerenti e non contraddittorie, ed è perciò una trasformazione tranquillamente praticata se opportuna; dato che la reale presenza di una forza fisica genera le stesse conseguenze teoriche del cambio di coordinate, l'introduzione di una forza apparente è una trasformazione altrettanto lecita. Il risultato, per nulla ovvio, è che il cambio di coordinate, che è una trasformazione che muta una costruzione geometrica e mentale senza toccare la realtà fisica degli oggetti e delle forze in gioco, sortisce gli stessi effetti di una variazione della realtà fisica che si deve descrivere. La nozione di forza apparente estende al modulo del moto (velocità e accelerazione) il principio di relatività, che in precedenza faceva dipendere dal sistema di riferimento solamente verso e direzione.
In contemporanea, le componenti della matrice diventano funzioni dello spazio-tempo; essendo delle variabili, descrivono un campo gravitazionale.
La deformazione del moto uniforme viene, quindi, interpretato come un effetto della gravitazione, «che occupa una posizione eccezionale nei confronti delle rimanenti forze, e soprattutto delle forze elettromagnetiche, in quanto le 10 funzioni che rappresentano il campo gravitazionale determinano contemporaneamente le proprietà dello spazio quadridimensionale».
Quindi, tali componenti sembrano più importanti di ogni altra forza della fisica, mentre la componente temporale appare la più rilevante di queste.
Quando le componenti sono costanti, gli effetti della gravitazione vengono trascurati (ciò non significa affatto che il moto avvenga in assenza di una forza di gravità misurabile). Per dedurre la formula di Newton, che considera tali effetti, è necessario rilasciare le ipotesi e considerare un sistema di riferimento in cui le componenti variano; per un rilascio graduale, si considerano sistemi in cui variano di piccole quantità, e che all'infinito spaziale tendono ancora ai valori della matrice. «In altre parole stiamo esaminando campi gravitazionali, generati esclusivamente da materia che si trova al finito», come quelli della teoria newtoniana.
Con riferimento all'equazione precedente, tre delle componenti possono assumere qualsiasi valore, raggiungendo qualunque velocità adimensionale p purché inferiore alla velocità della luce (ossia ). Nel sistema di riferimento adottato in tutta la relatività, la velocità è misurata da un numero puro, che vale 1 alla velocità della luce, che è la massima raggiungibile (quindi varia tra 0 e 1). Oltreché per una comodità di calcolo, la velocità è espressa come percentuale della velocità della luce, perché questa l'unica costante il cui valore di velocità resta invariato in qualunque sistema di riferimento.
- .
«Qualora ci si limiti al caso che quasi esclusivamente si presenta all'esperienza, in cui è piccolo rispetto alla velocità della luce», queste tre componenti sono infinitesimi del secondo ordine (hanno esponente pari a 2), trascurabili in prima approssimazione (vengono eliminati dal calcolo).
Nello studio del differenziale si è soliti iniziare dallo studio del differenziale primo. Limitandosi ai termini di ordine più basso, si ottiene inizialmente un'analisi più semplice, che considera meno termini. Adottare il punto di vista della prima approssimazione, significa troncare lo sviluppo al primo ordine (trascurando gli infinitesimi di ordine superiore al primo).
A questo punto, la sola componente rilevante è quella temporale. Bisogna notare che in queste righe di ipotesi, Einstein sta presentando la relatività come una generalizzazione alle alte velocità della gravitazione di Newton, che restava confinata all'esperienza quotidiana in cui le velocità sono molto minori della luce. Questo significa imporre , per cui i componenti di divengono degli infinitesimi.
L'equazione del moto del punto libero si riduce a:
- ,
avendo posto (ed essendosi ridotto) .
Sempre nell'ipotesi di campo gravitazionale quasi-statico, ossia generato da un moto di materia lento rispetto alla velocità della luce, le derivate miste (del tempo rispetto alle coordinate spaziali) sono trascurabili, l'equazione del moto diviene:
- .
La formula avrebbe lo stesso significato della gravitazione newtoniana, non deduce per via teorica il valore della costante, il quale resta non un risultato teorico, ma un numero misurato solamente per via sperimentale. Einstein riesce a dare una dimostrazione teorica della legge di gravità, pur non ricavandone la costante.
«Questa è l'equazione del moto del punto materiale in base alla teoria di Newton, in cui rappresenta il potenziale gravitazionale».
Note[modifica | modifica wikitesto]
Bibliografia[modifica | modifica wikitesto]
- (EN) Manfredo Perdigao do Carmo, Riemannian Geometry, 1994.
- (EN) Shoshichi Kobayashi, Katsumi Nomizu, Foundations of Differential Geometry, Vol. 1, Wiley-Interscience, 1996 (Nuova edizione), ISBN 0-471-15733-3.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sulla geodetica
Wikimedia Commons contiene immagini o altri file sulla geodetica
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) geodesic, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Geodetica, su MathWorld, Wolfram Research.
| Controllo di autorità | LCCN (EN) sh85053967 · GND (DE) 4156669-5 · J9U (EN, HE) 987007562985805171 |
|---|

















![{\displaystyle \gamma :[a,b]\to M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5c2d8d0dd04be91ac24d40469cc8b8ad0c7057d)



























![{\displaystyle \gamma ={\sqrt {[dx^{1}/dx^{4}]^{2}+[dx^{2}/dx^{4}]^{2}+[dx^{3}/dx^{4}]^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e59f1fd09b6b2b01b37979c8167a5c8275a57e8e)





