Problema di Keplero nella relatività generale
Il problema di Keplero nella relatività generale comporta la risoluzione del moto di due corpi sferici che interagiscono tra di loro per mezzo della gravitazione, come descritto dalla teoria della relatività generale.
In genere, e in questo articolo, un corpo viene ipotizzato avente una massa trascurabile rispetto alla massa di un altro corpo; questa è una buona approssimazione nel caso di un pianeta che ruota attorno al Sole, o di un fotone che passa da una stella. In tali casi, si può supporre che solo il corpo più pesante contribuisce alla curvatura dello spazio-tempo e che sia fisso nello spazio. Questo spazio-tempo curvo è descritto dalla soluzione di Schwarzschild per le equazioni di Einstein nel vuoto della relatività generale. Il moto del corpo più leggero (successivamente sarà chiamato "particella") è definito per mezzo delle geodetiche dello spazio-tempo della soluzione di Schwarzschild. Viene qui assunto che il corpo più leggero sia simile a un punto in modo che le forze di marea possano essere ignorate.
Queste soluzioni geodetiche giustificano la precessione anomala del pianeta Mercurio, che è la prova principale a sostegno della teoria della relatività generale. Esse descrivono anche la deflessione della luce in un campo gravitazionale, un'altra previsione notoriamente utilizzata come prova per la relatività generale.
Il decadimento orbitale dovuto all'emissione di radiazione gravitazionale non viene definito dalla soluzione di Schwarzschild.
Contesto storico e comprensione intuitiva[modifica | modifica wikitesto]

Nel 1859, Urbain Le Verrier scoprì che la precessione orbitale del pianeta Mercurio non era abbastanza rispetto a quella che avrebbe dovuto essere; l'ellisse della sua orbita ruotava (in precessione) leggermente più veloce di quanto previsto dalla teoria tradizionale della gravità newtoniana, anche dopo aver preso in considerazione tutti gli effetti degli altri pianeti.[1] L'effetto è piccolo (grosso modo 43 arcosecondi di rotazione per secolo), ma ben al di sopra dell'errore di misurazione (pressappoco 0,1 arcsecondi per secolo). Le Verrier comprese l'importanza della sua scoperta immediatamente, sfidando gli astronomi e i fisici a metterla in dubbio. Sono state proposte diverse spiegazioni classiche, come la polvere interplanetaria, lo schiacciamento polare inosservato del Sole, una luna di Mercurio ancora non scoperta, o un nuovo pianeta chiamato Vulcano.[2] Dopo che queste spiegazioni vennero ritenute di poco valore, alcuni fisici furono tentati dall'ipotesi più radicale, considerando sbagliata la legge del quadrato inverso della gravitazione di Newton. Per esempio, alcuni fisici proposero una legge di potenza con un esponente che fosse leggermente diverso da 2.
Altri ancora hanno sostenuto che la legge di Newton dovrebbe essere integrata con un potenziale dipendente dalla velocità. Tuttavia, questo implicava un conflitto con la dinamica celeste newtoniana. Nel suo trattato sulla meccanica celeste, Laplace aveva dimostrato che, se l'influenza gravitazionale non agisse istantaneamente, allora il moto dei pianeti stessi non conserverebbe esattamente la quantità di moto (parte del momento deve quindi essere attribuita al mediatore dell'Interazione gravitazionale, analogamente al momento che si attribuisce al mediatore della interazione elettromagnetica). Come si è osservato dal punto di vista newtoniano, se l'influenza gravitazionale si propaga a una velocità finita, allora in tutti i punti del tempo un pianeta viene attratto in un punto in cui il Sole era qualche tempo prima, e non verso la posizione istantanea del sole. In base all'ipotesi dei fondamenti classici, Laplace aveva dimostrato che se la gravità si propagasse a una velocità dell'ordine della velocità della luce allora il sistema solare sarebbe instabile, e non esistere per molto tempo. L'osservazione sul fatto che il sistema solare è vecchio permette di porre un limite inferiore alla velocità gravitazionale che è di molti ordini di grandezza più veloce della velocità della luce.[2] La valutazione di Laplace per la velocità gravitazionale non è esatta, perché in una teoria di campo che rispetti il principio di relatività, l'attrazione di una carica puntiforme che si muove a una velocità costante è verso la posizione istantanea estrapolata, non verso la posizione apparente che sembra occupi quando si osserva[3].
Per evitare questi problemi, tra il 1870 e il 1900 molti scienziati utilizzavano le leggi dell'elettrodinamica di Wilhelm Eduard Weber, Carl Friedrich Gauß, Bernhard Riemann per produrre orbite stabili e spiegare lo spostamento del perielio dell'orbita di Mercurio. Nel 1890 Lévy riuscì a farlo combinando le leggi di Weber e di Riemann, per cui la velocità gravitazionale è nella sua teoria uguale a quella della luce. E in un altro tentativo Paul Gerber (1898) riuscì ugualmente a ottenere la formula corretta per lo spostamento del perielio (la quale era identica a quella usata più tardi da Einstein)[4]. Tuttavia, dato che le leggi fondamentali di Weber e di altri erano errate (per esempio, la legge di Weber venne rimpiazzata dalla teoria di Maxwell), quelle ipotesi vennero rifiutate.[5] Un altro tentativo fatto da Hendrik Lorentz (1900), che aveva già utilizzato la teoria di Maxwell, produsse un spostamento del perielio troppo basso.[2]
Intorno al 1904–1905, i lavori di Hendrik Lorentz, Henri Poincaré e infine la teoria ristretta della relatività di Albert Einstein, escludevano la possibilità di propagazione di qualsiasi effetto più veloce della velocità della luce. Ne consegue che la legge gravitazionale di Newton avrebbe dovuto essere sostituita con un'altra legge, compatibile con il principio di relatività, nonostante il limite newtoniano restasse valido nelle circostanze in cui gli effetti relativistici fossero trascurabili. Tali tentativi sono stati fatti da Henri Poincaré (1905), Hermann Minkowski (1907) e Arnold Sommerfeld (1910).[6] Nel 1907 Einstein arrivò a concludere che per raggiungere questo obiettivo fosse necessaria un erede della relatività ristretta. Dal 1907 al 1915, Einstein tenta gradualmente di spingersi verso una nuova teoria, usando il suo principio di equivalenza come concetto chiave per raggiungere lo scopo. Secondo questo principio, un campo gravitazionale uniforme agisce allo stesso modo su tutto quanto vi è all'interno di esso e, di conseguenza, non può essere rilevato da un osservatore in caduta libera. Al contrario, tutti gli effetti gravitazionali locali dovrebbero essere riproducibili in un sistema di riferimento che acceleri in modo lineare, e viceversa. Così, la gravità agisce come una forza fittizia come la forza centrifuga o la forza di Coriolis, risultante da un sistema di riferimento accelerato; tutte le forze fittizie sono proporzionali alla massa inerziale, proprio come la gravità. Per conciliare la gravità con la relatività speciale incorporando il principio di equivalenza, qualcosa deve essere sacrificato; quel qualcosa fu il presupposto classico di lunga data che considerava il nostro spazio soggetto alle leggi della geometria euclidea, per es., il fatto che il teorema di Pitagora sia vero sperimentalmente. Einstein utilizzò una geometria più generale, la pseudo-geometria di Riemann, per consentire la curvatura di spazio e tempo, condizione necessaria per la riconciliazione; dopo otto anni di lavoro (1907–1915), riuscì a scoprire il modo preciso in cui spazio-tempo sarebbero curvi al fine di riprodurre le leggi fisiche osservate in natura, in particolare la gravitazione. La gravità è distinta dalle forze fittizie, centrifughe e di Coriolis, nel senso che la curvatura dello spazio-tempo è considerato come reale fisicamente, mentre le forze fittizie non sono considerate come forze. Le prime vere soluzioni delle sue equazioni di campo spiegavano la precessione anomala di Mercurio prevedendo un'insolita curvatura della luce, la quale venne confermata dopo che la sua teoria venne pubblicata. Queste soluzioni sono spiegate qui di seguito.
Ambito geometrico[modifica | modifica wikitesto]
Nella normale geometria euclidea, i triangoli obbediscono al teorema di Pitagora, il quale stabilisce che la distanza al quadrato tra due punti nello spazio è la somma dei quadrati delle sue componenti perpendicolari
dove , e rappresentano le differenze infinitesimali tra i due punti lungo gli assi , e di un sistema di coordinate cartesiane (aggiungere qui la figura). Ora immaginate un mondo in cui questo non è del tutto vero, un mondo dove la distanza è invece data da
dove , e sono funzioni arbitrarie della posizione. Non è difficile immaginare un siffatto mondo: noi ci viviamo. La superficie del mondo è curvo, e ciò rende vana la possibilità di farne una mappa perfettamente precisa e piana. I sistemi di coordinate non cartesiane descrivono bene questo, per esempio, nelle coordinate sferiche (, , ), la distanza euclidea può essere scritta
Un altro esempio sarebbe un mondo in cui i regoli utilizzati per misurare la lunghezza sarebbero inaffidabili, mutando la loro lunghezza con la loro posizione e anche la loro orientazione. Nel caso più generale, si devono consentire i termini trasversali (cross-terms) quando si calcola la distanza :
dove nove funzioni , costituiscono il tensore metrico, il quale definisce la geometria dello spazio nella geometria di Riemann. Nell'esempio delle coordinate sferiche di cui sopra, non vi sono termini trasversali; le sole componenti del tensore metrico diverse da zero sono , e .
Nella sua teoria ristretta della relatività, Albert Einstein dimostrava che la distanza tra due punti spaziali non è costante, ma dipende dal moto dell'osservatore. Tuttavia, vi è una misura di separazione tra due punti nello spazio-tempo — chiamata "tempo proprio" e indicata con il simbolo — che è invariante; in altre parole, non dipende dal moto dell'osservatore.
la quale può essere scritta con le coordinate sferiche nel seguente modo:
Questa formula è l'estensione naturale del teorema di Pitagora e analogamente regge solo quando non c'è curvatura dello spazio-tempo. Nella relatività generale, comunque, spazio e tempo possono avere curvatura, quindi questa formula della distanza deve essere modificata in una forma più generale:
così come abbiamo generalizzato la formula per misurare la distanza sulla superficie della Terra. La forma esatta della metrica dipende dalla massa gravitante, momento ed energia, come descritta dalle equazioni di campo di Einstein. Einstein sviluppò tali equazioni di campo per soddisfare le leggi della natura allora conosciute ma, ciò nonostante, esse hanno previsto fenomeni mai visti prima (come la curvatura della luce a causa della gravità), confermati in seguito.
Metrica di Schwarzschild[modifica | modifica wikitesto]
Una soluzione per le equazioni di campo di Einstein è la metrica di Schwarzschild, corrispondente al campo gravitazionale di un corpo sfericamente simmetrico, non rotante, senza carica e di massa . La soluzione di Schwarzschild può essere scritta come:
dove:
- è il tempo proprio (il tempo misurato da un orologio che si muove insieme alla particella) in secondi,
- è la velocità della luce in metri al secondo,
- è la coordinata del tempo (misurata da un orologio stazionario all'infinito) in secondi,
- è la coordinata radiale (circonferenza di un cerchio centrato sulla stella diviso per ) in metri,
- è la colatitudine (angolo da Nord) in radianti,
- è la longitudine in radianti, e
- è il raggio di Schwarzschild (in metri) del corpo massivo, il quale è correlato alla sua massa da
- dove è la costante gravitazionale.[7]
La teoria newtoniana classica della gravità è recuperata nel limite come il rapporto va a zero. In questo limite, la metrica ritorna nella forma data sopra per la relatività ristretta. In pratica, questo rapporto è quasi sempre estremamente piccolo. Per esempio, il raggio di Schwarzschild della Terra è grosso modo 9 mm, laddove un satellite in un'orbita geosincrona ha un raggio che è di circa quattro bilioni di volte più grande, a 42.164 km. Anche per la superficie della Terra, le correzioni per la gravità newtoniana sono soltanto una parte su un bilione. Il rapporto diventa grande solo vicino ai buchi neri e agli oggetti ultra-densi come le stelle di neutroni.
Equazione geodetica[modifica | modifica wikitesto]
Secondo la teoria di Einstein della relatività generale, le particelle di massa trascurabile viaggiano lungo le geodetiche nello spazio-tempo. In uno spazio-tempo non curvo, lontano dalla sorgente di gravità, queste geodetiche corrispondono a linee rette; tuttavia, possono deviare dalla linee rette quando lo spazio-tempo è curvo. L'equazione per le linee geodetiche è[8]
dove rappresenta il simbolo di Christoffel e la variabile parametrizza il percorso della particella attraverso lo spazio-tempo, la sua cosiddetta linea di universo. Il simbolo di Christoffel dipende soltanto dal tensore metrico , o piuttosto da come esso muta con la posizione. La variabile è una costante multipla del tempo proprio per orbite di tipo tempo (che sono percorse da particelle massive), ed è di solito considerata uguale a essa. Per le orbite di tipo luce (o nulle) (le quali sono percorse da particelle senza massa come i fotoni), il tempo proprio è zero e, a rigore, non può essere usato come la variabile . Ciò nonostante, le orbite di tipo luce possono essere derivate come il limite ultrarelativistico delle orbite di tipo tempo, vale a dire, il limite come la massa della particella va a zero mentre mantiene fissa la sua energia complessiva.
Possiamo semplificare il problema utilizzando la simmetria per eliminare una variabile presa in considerazione. Poiché la metrica di Schwarzschild è simmetrica di circa , ogni geodetica che inizia a muoversi in quel piano rimarrà in quel piano indefinitamente (il piano è totalmente geodetico). Quindi, orientiamo il sistema di coordinate in modo che l'orbita della particella venga a trovarsi in quel piano, e fissiamo la coordinata come in modo che la metrica (di questo piano) si semplifichi in:
Due costanti di moto possono essere dunque identificate (cfr. la derivazione data nell'approccio lagrangiano)
Sostituendo queste costanti dentro la definizione della metrica di Schwarzschild
si ottiene l'equazione di moto per la particella:
La dipendenza dal tempo proprio può essere eliminata usando la definizione di
che fornisce l'equazione per l'orbita:
dove, per brevità, le due scale di lunghezza, e , vengono definite da:
La stessa equazione può anche essere derivata usando un approccio lagrangiano[9] o l'equazione di Hamilton – Jacobi[10] (vedi sotto). La soluzione dell'equazione orbitale è:
Formula approssimata per la curvatura della luce[modifica | modifica wikitesto]

Nel limite come la massa della particella va a zero (o, in modo equivalente, come la scala di lunghezza va all'infinito), l'equazione per l'orbita diventa:
Espandendo in potenze di , il termine di ordine dominante in questa formula dà la deflessione angolare approssimata per una particella senza massa che viene dall'infinito e ritorna all'infinito:
Qui, può essere interpretata come la distanza di un approccio più stretto. Sebbene questa formula sia approssimata, essa è precisa per la maggior parte delle misurazioni del fenomeno delle lenti gravitazionali, dovuto alla piccolezza del rapporto . Per la luce radente la superficie del sole, la deflessione angolare approssimativa è di circa 1,75 arcosecondi.
Relazione della meccanica classica e la precessione delle orbite ellittiche[modifica | modifica wikitesto]
L'equazione di moto per la particella derivata sopra
può essere riscritta usando la definizione del raggio di Schwarzschild come:
che è equivalente a una particella che si muove in un potenziale effettivo unidimensionale
I primi termini sono energie classiche ben note, essendo la prima l'energia potenziale gravitazionale attrattiva newtoniana e la seconda corrisponde all'energia potenziale "centrifuga" repulsiva; Tuttavia, il terzo termine è un è un'energia attrattiva unica per la relatività generale. Come mostrato sotto e altrove, questa energia cubica-inversa causa gradualmente la precessione delle orbite ellittiche di un angolo per la rivoluzione:
dove è il semi-asse maggiore ed è l'eccentricità.
Il terzo termine è attrattivo e domina in valori di piccoli, dando un raggio critico interno dove una particella è attratta inesorabilmente verso l'interno per ; questo raggio interno è una funzione del momento angolare della particella per unità di massa o, in modo equivalente, la scala di lunghezza definita sopra.
Orbite circolari e loro stabilità[modifica | modifica wikitesto]
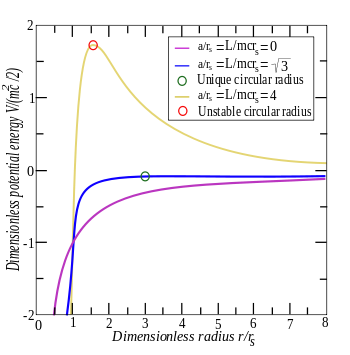
Il potenziale effettivo può essere riscritto nei termini delle lunghezze e
Le orbite circolari sono possibili quando la forza effettiva è zero:
i.e., quando due forze attrattive — la gravità newtoniana (primo termine) e l'attrazione unica per la relatività generale (terzo termine) — sono esattamente bilanciati dalla forza centrifuga repulsiva (secondo termine). Ci sono due raggi dove questo bilanciamento può accadere, definito qui come e :
che sono ottenute usando la formula quadratica. Il raggio interno è instabile, poiché la terza forza attrattiva aumenta molto più velocemente delle altre due forze quando diventa piccolo; se la particella scivola leggermente verso l'interno da (dove tutte e tre le forze sono in equilibrio), la terza forza domina le altre due, trascinando la particella inesorabilmente verso l'interno per . Nel raggio esterno, comunque, le orbite circolari sono stabili; il terzo termine è meno importante e il sistema si comporta in modo più simile al problema di Keplero non-relativistico.
Quando è molto più grande di (caso classico), queste formule diventano approssimativamente:

Sostituendo le definizioni di e in si ottiene la formula classica per una particella orbitante una massa in un cerchio:
dove è la velocità angolare orbitale della particella. Questa formula è ottenuta nella meccanica non-relativistica impostando la forza centrifuga uguale alla forza gravitazionale newtoniana:
dove è la massa ridotta.
Nella nostra notazione, la velocità orbitale classica è uguale a:
Nell'altro estremo, quando avvicina soprattutto a , i due raggi convergono in un unico valore
Le soluzioni quadratiche sopra assicurano che è sempre maggiore di , laddove si trova fra e . Le orbite circolari più piccole di non sono possibili. Per le particelle senza massa, va all'infinito, il che implica che vi sia un'orbita circolare per i fotoni per . La sfera di questo raggio è talvolta nota come sfera fotonica.
Precessione delle orbite ellittiche[modifica | modifica wikitesto]

La velocità (rate) di precessione orbitale può essere ricavata utilizzando questo potenziale effettivo radiale . Una piccola deviazione radiale da un'orbita circolare di raggio oscillerà stabilmente con una frequenza angolare
che è pari a:
Prendendo la radice quadrata di entrambi i lati e espandendo usando il teorema binomiale si ottiene la formula:
Moltiplicando per il periodo di una rivoluzione si ottiene la precessione dell'orbita per rivoluzione:
dove abbiamo usato e la definizione della scala di lunghezza . Sostituendo la definizione del raggio di Schwarzschild si ha:
Questa può essere semplificata usando il semiasse dell'orbita ellittica e l'eccentricità correlata tramite la formula:
per dare la forma più comune dell'angolo di precessione
Soluzione orbitale usando funzioni ellittiche[modifica | modifica wikitesto]
L'equazione per l'orbita
può essere semplificata introducendo una variabile senza dimensione:
in modo che si riduca a:
dove la costante, i coefficienti senza dimensione e sono definiti tramite
La soluzione di questa equazione orbitale è data da:
Ne consegue che, fino ad un cambiamento di fase, , dove è la funzione ellittica di Weierstrass con i parametri e , e è una costante di integrazione (possibilmente complessa).
Carattere qualitativo di possibili orbite[modifica | modifica wikitesto]
Le orbite sono definite dall'equazione di moto:
Se il discriminante è maggiore di zero, l'equazione cubica
avrà tre radici reali e distinte, , ed , che possono essere elencate in ordine decrescente:
In tali casi, la soluzione è una funzione ellittica con due semi-periodi, uno completamente reale
e un altro completamente immaginario
- .
La radice restante definisce un semi-periodo complesso . Questi tre semi-periodi sono correlati alle radici corrispondenti per mezzo dell'equazione , dove può essere uguale a o . Quindi, è posto uguale a ognuno di questi semi-periodi, la derivata di è zero, indicando un periapside o un apoapside, i punti di approccio rispettivamente più vicini o più lontani.
- ,
dato che
- .
Le radici sono i valori critici di per quanto riguarda , i.e., i valori dove la derivata è uguale a zero.
Il carattere qualitativo delle orbite dipende dalla scelta di . Le soluzioni con pari a corrispondono a orbite oscillatorie che variano tra e , oppure divergono all'infinito . Diversamente, le soluzioni con pari a (o a ogni altro numero reale) corrispondono a orbite che decadono a raggio zero, dato che (per essere un numero reale) non può essere inferiore a e perciò aumenta inesorabilmente all'infinito.
Orbite quasi ellittiche[modifica | modifica wikitesto]
Le soluzioni in cui pari a danno un valore reale di a condizione che l'energia soddisfi la disuguaglianza . Per tali soluzioni, la variabile è confinata tra . Se entrambe le radici sono maggiori di , allora non diventerà mai , il punto in cui il raggio va all'infinito. Perciò, tali soluzioni corrispondono a un'orbita ellittica in graduale precessione. Dato che la particella (o pianeta) ruota intorno alla origine, il suo raggio oscilla tra un raggio minimo
e un raggio massimo
- .
che corrisponde al valore di ai due estremi (extrema) del raggio. La periodicità reale della funzione ellittica di Weierstrass è ; così la particella ritorna allo stesso raggio dopo aver girato con un angolo di , che può non essere uguale a . Perciò, l'orbita è in precessione. In generale, la quantità di precessione per orbita () è abbastanza piccola.
Orbite circolari stabili[modifica | modifica wikitesto]
Un caso speciale si verifica quando , i.e., due delle radici di sono uguali e negative, mentre la terza è positiva. In questo caso c'è una soluzione con la costante , pari alla radice ripetuta, . Ciò corrisponde a orbite circolari, in particolare, alla soluzione classica derivata sopra; come qui dimostrato, i raggi di queste orbite devono essere maggiori di . Tali orbite circolari sono stabili, perché una piccola perturbazione dei parametri separerebbe le radici ripetute, risultanti in un'orbita quasi-ellittica. Ad esempio, dando un piccolo "colpetto" radiale a una particella in una classica orbita circolare la si spinge in un'orbita ellittica che gradualmente va in precessione.
Orbite illimitate[modifica | modifica wikitesto]
Un'orbita illimitata si verifica quando va all'infinito, corrispondente a . Le orbite illimitate corrispondono a un'orbita oscillatoria in cui cade tra le due radici limitanti, i.e., quando .
Orbite circolari asintotiche[modifica | modifica wikitesto]
Un altro caso particolare succede quando , i.e., due delle radici di sono uguali e positive, mentre la terza radice è negativa. Indicando la radice ripetuta con , le orbite sono asintoticamente circolari all'infinito positivo e negativo:
come può essere verificato per mezzo della sostituzione. Come va all'infinito positivo o negativo, l'orbita si avvicina asintoticamente al cerchio:
In tali casi, il raggio dell'orbita deve rimanere tra e .
La formula asintotica può anche essere derivata dall'espressione per la funzione ellittica di Weierstrass in termini di funzioni ellittiche di Jacobi
dove e il modulo pari a:
Nel limite, come si avvicina a , il modulo tende a e va a . Infine scegliendo come numero immaginario (un quarto periodo) dà la formula asintotica sopra.
Orbite decadenti[modifica | modifica wikitesto]
Le soluzioni reali per in cui è pari a (o a qualche altro numero reale) hanno la proprietà per cui non è mai minore di . Dato che l'equazione di moto
è positiva per tutti i valori di , aumenta illimitatamente, corrispondente alla particella che cade inesorabilmente per l'origine .

Correzioni alle soluzioni geodetiche[modifica | modifica wikitesto]
Secondo la relatività generale, due corpi girando uno sull'altro emetteranno radiazione gravitazionale, facendo sì che le orbite siano leggermente diverse rispetto alle geodetiche calcolate sopra. Questo è stato osservato indirettamente in un sistema di stella binaria conosciuto come PSR B1913+16, per cui Russell Alan Hulse e Joseph Hooton Taylor Jr. vennero insigniti nel 1993 del Premio Nobel per la fisica. Le due stelle di neutroni di questo sistema sono estremamente vicine e ruotano quasi l'un l'altra molto velocemente, completando una rivoluzione in più o meno 465 minuti. La loro orbita è fortemente ellittica, con un'eccentricità di 0,62 (62%). Secondo la relatività generale, il breve periodo orbitale e l'alta eccentricità farebbero del sistema un eccellente emettitore di radiazione gravitazionale, perdendo così energia e riducendo ulteriormente il periodo orbitale. La diminuzione osservata nel periodo orbitale per più di trent'anni combacia con le previsioni della relatività generale anche nell'ambito delle più precise misurazioni. La relatività generale prevede che, nel giro di altri 300 milioni di anni, questi due astri si metteranno a spirale l'uno nell'altro.

Sono state calcolate le formule che definiscono la perdita di energia e il momento angolare dovuto alla radiazione gravitazionale dei due corpi del problema di Kepler.[11] Il tasso di energia persa (in media su un'orbita completa) è dato da[12]
dove è l'eccentricità orbitale e è il semiasse maggiore dell'orbita ellittica. Le parentesi angolari sul lato sinistro dell'equazione rappresentano la media su una singola orbita. Allo stesso modo, il tasso medio di perdita del momento angolare è uguale a:
Le perdite in energia e momento angolare aumentano significativamente come l'eccentricità si avvicina a , i.e., come l'ellisse dell'orbita diventa sempre più allungata. Anche le perdite di radiazione aumentano significativamente con il diminuire della dimensione dell'orbita.
Derivazioni matematiche dell'equazione orbitale[modifica | modifica wikitesto]
Approccio di Hamilton–Jacobi[modifica | modifica wikitesto]
L'equazione orbitale può essere derivata dall'equazione di Hamilton-Jacobi. Il vantaggio di questo approccio è che si mette sullo stesso piano il moto della particella con la propagazione di un'onda, e porta ordinatamente dentro la derivazione della deflessione della luce per mezzo della gravità nella relatività generale, attraverso il principio di Fermat. L'idea di base è che, a causa del rallentamento gravitazionale del tempo, le parti di un fronte d'onda più vicino a una massa gravitante si muovono più lentamente rispetto a quelle più lontane, curvando così la direzione di propagazione del fronte dell'onda (aggiungi figura).
Usando la covarianza generica, l'equazione di Hamilton-Jacobi per una singola particella di coordinate arbitrarie può essere espressa come:
Usando la metrica di Schwarzschild , questa equazione diventa:
dove abbiamo di nuovo orientato il sistema di coordinate sferiche con il piano dell'orbita. Il tempo e la longitudine sono coordinate cicliche, in modo che la soluzione per l'azione possa essere scritta come:
dove e rappresentano di nuovo rispettivamente l'energia della particella e il momento angolare. L'equazione di Hamilton-Jacobi fornisce una soluzione integrale per la parte radiale dell'azione:
Prendendo la derivata dell'azione nel solito modo
si ottiene l'equazione orbitale derivata precedentemente:
Questo approccio può essere anche utilizzato per derivare la velocità (rate) di precessione orbitale in modo elegante.[13]
Nel limite di massa zero (o, in modo equivalente, infinito), la parte radiale della funzione principale di Hamilton diventa:
da cui può essere derivata l'equazione per la deflessione della luce.
Approccio lagrangiano[modifica | modifica wikitesto]
Nella relatività generale, le particelle libere di massa trascurabile seguono le geodetiche nello spazio-tempo, a causa del principio di equivalenza. Le geodetiche nello spazio-tempo sono definite come curve per cui le piccole variazioni locali nella loro coordinate (tenendo i loro eventi estremi fissi) non apportano modifiche significative nella loro lunghezza complessiva . Ciò può essere espresso matematicamente usando il calcolo delle variazioni:
dove è il tempo proprio, è la lunghezza dell'arco nello spazio-tempo e viene definito come:
in analogia con l'energia cinetica. Se la derivata rispetto al tempo proprio è rappresentata per brevità da un punto
può essere scritta come:
I fattori della costante (come o la radice quadrata di ) non incidono sulla risposta al problema variazionale, quindi, tenendo la variazione all'interno dell'integrale si ottiene il principio di Hamilton:
La soluzione del problema variazionale è data dalle equazioni di Lagranges:
Quando applicate a e , queste equazioni rivelano due costanti di moto
le quali possomo essere scritte come le equazioni per e
Come mostrato sopra, con la sostituzione di queste equazioni dentro la definizione della metrica di Schwarzschild si ottiene l'equazione per l'orbita.
Principio di Hamilton[modifica | modifica wikitesto]
L'integrale dell'azione per una particella influenzata soltanto dalla gravità è:
dove è il tempo proprio e è ogni parametrizzazione regolare della linea di universo della particella. Se a questa si applica il calcolo delle variazioni, si ottengono di nuovo le equazioni per una geodetica. I calcoli sono semplificati, se prima prendiamo la variazione del quadrato dell'integrando. Per la metrica e le coordinate di questo caso, quella quadrata è:
Prendendo la variazioni di questa, otteniamo:
Se variamo soltanto rispetto alla longitudine , otteniamo:
dividiamo per per ottenere la variazione dell'integrando stesso
Perciò abbiamo:
L'integrazione delle parti dà
La variazione della longitudine è assunta uguale a zero nei punti finali, così il primo termine scompare. L'integrale può essere fatto diverso da zero tramite una scelta ostinata (perverse) di salvo che l'altro fattore interno sia ovunque zero. Così otteniamo l'equazione di moto:
Se variamo soltanto rispetto al tempo , otteniamo:
dividiamo per per ottenere la variazione dell'integrando stesso
Così abbiamo:
L'integrazione delle parti dà
- ,
fornendo l'equazione di moto:
Se integriamo queste equazioni di moto e determiniamo le costanti di integrazione, otteniamo di nuovo le equazioni
Queste due equazioni per le costanti di moto ed possono essere combinate per formare un'equazione che è valida anche per i fotoni e altre particelle senza massa per cui il tempo proprio lungo una geodetica è zero.
Note[modifica | modifica wikitesto]
- ^ (EN) U.J.J. Le Verrier, Titolo sconosciuto, in Comptes Revues d'Academie de la Science de Paris, vol. 49, 1859, pp. 379–?.
- ^ a b c Pais 1982
- ^ Le conferenze di Feynman sulla Fisica, vol. II, offrono una trattazione accurata del problema analogo nell'elettromagnetismo. Feynman dimostra che, per una carica in moto, il campo non radiativo è un'attrazione/repulsione, non verso la posizione apparente delle particelle, ma verso la posizione estrapolata nell'ipotesi che la particella prosegua in linea retta e a velocità costante. Questa è una proprietà notevole dei potenziali di Liénard-Wiechert. Presumibilmente lo stesso vale per la gravità linearizzata.
- ^ (DE) Paul Gerber, Die räumliche und zeitliche Ausbreitung der Gravitation, in Zeitschrift für Mathematik und Physik, vol. 43, 1898, pp. 93–104.
- ^ Roseveare 1982
- ^ Walter 2007
- ^ Landau 1975.
- ^ Weinberg 1972.
- ^ Whittaker 1937.
- ^ Landau e Lifshitz (1975), pp. 306–309.
- ^ (EN) Peters P.C., Mathews J., Gravitational Radiation from Point Masses in a Keplerian Orbit, in Physical Review, vol. 131, 1963, pp. 435–?, DOI:10.1103/PhysRev.131.435.
- ^ Landau e Lifshitz, p. 356–357.
- ^ Landau e Lifshitz (1975), pp. 307–308.
Bibliografia[modifica | modifica wikitesto]
- (EN) R Adler, Bazin M.; Schiffer M., Introduction to General Relativity, New York, McGraw-Hill Book Company, 1965, pp. 177–193, ISBN 978-0-07-000420-7.
- (EN) A. Einstein, The Meaning of Relativity, 5ª ed., Princeton, NJ, Princeton University Press, 1956, pp. 92–97, ISBN 978-0-691-02352-6.
- (EN) Y Hagihara, Theory of the relativistic trajectories in a gravitational field of Schwarzschild, in Japanese Journal of Astronomy and Geophysics, vol. 8, 1931, pp. 67–176, ISSN 0368-346X.
- (EN) C. Lanczos, The Variational Principles of Mechanics, 4ª ed., New York, Dover Publications, 1986, pp. 330–338, ISBN 978-0-486-65067-8.
- (EN) L.D. Landau e E.M. Lifshitz, The Classical Theory of Fields, Course of Theoretical Physics, vol. 2, 4ª inglese rivisitata, New York, Pergamon Press, 1975, pp. 299–309, ISBN 978-0-08-018176-9.
- (EN) C.W. Misner, Thorne, K e Wheeler, J.A., Gravitation, San Francisco, W. H. Freeman, 1973, capitolo 25 (pp. 636–687), §33.5 (pp. 897–901), and §40.5 (pp. 1110–1116), ISBN 978-0-7167-0344-0. (vedi Gravitazione (libro).)
- (EN) A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein, Oxford University Press, 1982, pp. 253–256, ISBN 0-19-520438-7.
- (EN) W. Pauli, Theory of Relativity, Tradotto da G. Field, New York, Dover Publications, 1958, pp. 40–41, 166–169, ISBN 978-0-486-64152-2.
- (EN) W. Rindler, Essential Relativity: Special, General, and Cosmological, 2ª rivisitata, New York, Springer Verlag, 1977, pp. 143–149, ISBN 978-0-387-10090-6.
- (EN) Roseveare, N.T., Mercury's perihelion, from Leverrier to Einstein, Oxford, University Press, 1982, ISBN 0-19-858174-2.
- (EN) J.L. Synge, Relativity: The General Theory, Amsterdam, North-Holland Publishing, 1960, pp. 289–298, ISBN 978-0-7204-0066-3.
- (EN) R.M. Wald, General Relativity, Chicago, The University of Chicago Press, 1984, pp. 136–146, ISBN 978-0-226-87032-8.
- (EN) Walter, S., Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910, in Renn, J. (a cura di), The Genesis of General Relativity, vol. 3, Berlino, Springer, 2007, pp. 193–252. URL consultato il 10 maggio 2010 (archiviato dall'url originale il 30 gennaio 2009).
- (EN) S. Weinberg, Gravitation and Cosmology, New York, John Wiley and Sons, 1972, pp. 185–201, ISBN 978-0-471-92567-5.
- (EN) E.T. Whittaker, A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies, 4ª ed., New York, Dover Publications, 1937, pp. 389–393, ISBN 978-1-114-28944-4.




























































![{\displaystyle {\frac {1}{2}}m\left({\frac {dr}{d\tau }}\right)^{2}=\left[{\frac {E^{2}}{2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{2mr^{2}}}+{\frac {GML^{2}}{c^{2}mr^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5318d7d3eb4d8c6b9e66dbf0effffc5297383e75)









![{\displaystyle V(r)={\frac {mc^{2}}{2}}\left[-{\frac {r_{s}}{r}}+{\frac {a^{2}}{r^{2}}}-{\frac {r_{s}a^{2}}{r^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1dc9d62dd01e10253063b8383c4cd9b055d5d27)
![{\displaystyle F=-{\frac {dV}{dr}}=-{\frac {mc^{2}}{2r^{4}}}\left[r_{s}r^{2}-2a^{2}r+3r_{s}a^{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88f2da9ae5e8b7b5bd74690d22f4996401b536c)

















![{\displaystyle \omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r=r_{\mathrm {outer} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)






















































































![{\displaystyle {\frac {d}{d\tau }}\left[r^{2}{\frac {d\varphi }{d\tau }}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e7587be0611673e3ad751e0db29a70635d76108)
![{\displaystyle {\frac {d}{d\tau }}\left[\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e43df66c44d864551699f249c91284633e11a414)


![{\displaystyle \delta \left(c{\frac {d\tau }{dq}}\right)^{2}=2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aca95a35ae6a9911e1399bd759b8ad167d4cffd)




![{\displaystyle 0=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a396d0dc7e209a343b1633faeaa37953cb250d63)
![{\displaystyle {\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8da37d5aeba3fee4873426b62835abfb109cda2a)



![{\displaystyle 0=c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\delta t-\int {{\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]\delta tdq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9416a3e0124397cc488193c1d4cd41e2c81dcd)
![{\displaystyle {\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9493bddcfc4668a0946abc50b36949dfe5e472f5)

