Teorema di Pitagora

In un triangolo rettangolo la somma delle aree dei quadrati costruiti sui cateti (blu e rosso) è uguale all'area del quadrato costruito sull'ipotenusa (viola).

Animazione a prova del Teorema di Pitagora

Il teorema di Pitagora è un teorema della geometria euclidea che stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo.

Si può considerare un caso speciale, per i triangoli rettangoli, del teorema del coseno.

Origine

Visualizzazione del caso del triangolo (3,4,5) contenuta nel testo cinese Chou Pei Suan Ching (scritto tra il 200 a.C. e il 200 d.C.)

Quello che modernamente conosciamo come teorema di Pitagora viene attribuito al filosofo e matematico Pitagora. In realtà il suo enunciato (ma non la sua dimostrazione) era già noto ai Babilonesi. Viene a volte affermato che il teorema di Pitagora fosse noto agli antichi Egizi: Carl Boyer esclude questa ipotesi, basandosi sull'assenza del teorema dai papiri matematici rinvenuti. Era conosciuto anche in Cina e sicuramente in India, come dimostrano molte scritture fra cui lo Yuktibhāṣā e gli Śulbasūtra. Non sono note dimostrazioni del teorema considerate tutt'oggi valide e antecedenti o coeve a Pitagora.

Enunciato

In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente all'unione dei quadrati costruiti sui cateti.

oppure:

In ogni triangolo rettangolo l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.

L'uso dell'aggettivo uguale invece di equivalente richiede di riferirsi o alle aree dei quadrati "costruiti" sui cateti e sull'ipotenusa (area intesa come misura dell'estensione di una superficie), oppure ai quadrati delle lunghezze dei cateti/quadrato della lunghezza dell'ipotenusa. La possibile ambivalenza della lingua italiana deriva dal fatto che, in assenza del termine costruito, la parola quadrato può definire sia la superficie della figura geometrica in quanto tale, sia la generica operazione di elevamento alla seconda potenza.

In altre lingue, segnatamente in inglese, francese e spagnolo, nell'enunciato del teorema di Pitagora si preferisce parlare di quadrati (delle lunghezze) dei cateti e dell'ipotenusa, il che consente il semplice utilizzo dei termini equal (in inglese), égal (in francese), igual (in spagnolo). Per esempio, in spagnolo, el cuadrado de la hipotenusa significa, senza ambiguità, il "quadrato (della misura) dell'ipotenusa".

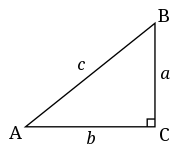
Dato un triangolo rettangolo di lati $a$, $b$ e $c$, ed indicando con $c$ la sua ipotenusa e con $a$ e $b$ i suoi cateti, il teorema è espresso dall'equazione:

$a^{2}+b^{2}=c^{2},$

o, esplicitando $c$:

${\sqrt {a^{2}+b^{2}}}=c.$

Le misure dei cateti sono perciò:

${\sqrt {c^{2}-b^{2}}}=a,$

e

${\sqrt {c^{2}-a^{2}}}=b.$

Una terna di numeri interi positivi ${a,b,c}$ che soddisfi il teorema di Pitagora si dice terna pitagorica.

Viceversa, ogni triangolo in cui i tre lati verifichino questa proprietà è rettangolo: questo teorema, con la sua dimostrazione, appare nell'ultimo enunciato del primo libro di Elementi.

Dimostrazioni

Animazione di una dimostrazione

La dimostrazione classica del teorema di Pitagora completa il primo libro degli Elementi di Euclide e ne costituisce il filo conduttore. Dato che richiede il postulato delle parallele, esso non vale nelle geometrie non-euclidee e nella geometria neutrale. Nel testo di Euclide la dimostrazione del teorema è immediatamente preceduta dalla dimostrazione della costruibilità dei quadrati. L'esistenza stessa dei quadrati dipende infatti dal postulato delle parallele e viene meno nelle geometrie non euclidee. Questo aspetto del problema è in genere trascurato nella didattica contemporanea, che tende spesso ad assumere come ovvia l'esistenza dei quadrati.

La dimostrazione del teorema di Pitagora consiste nel riempire uno stesso quadrato di lato uguale alla somma dei cateti prima con quattro copie del triangolo rettangolo più il quadrato costruito sull'ipotenusa e poi con quattro copie del triangolo rettangolo più i quadrati costruiti sui cateti, come in figura.

Essendo il teorema uno dei più noti della storia della matematica, ne esistono moltissime dimostrazioni, in totale alcune centinaia, opera di matematici, astronomi, agenti di cambio, per esempio un presidente statunitense James A. Garfield e Leonardo da Vinci. Per questo teorema sono state classificate dallo scienziato statunitense Elisha Scott Loomis 371 differenti dimostrazioni, che sono state pubblicate nel 1927 nel suo libro The Pythagorean Proposition.

Dimostrazione di Abu'l-Wafa

Dimostrazione di Abu'l-Wafa' i Perigal

La dimostrazione attribuita al matematico e astronomo persiano Abu'l-Wafa verso la fine del X secolo e riscoperta dall'agente di cambio Henry Perigal (trovata nel 1835-1840, pubblicata nel 1872 e successivamente nel 1891) si basa sulla scomposizione del quadrato costruito sul cateto maggiore, in giallo nell'immagine: tagliandolo infatti con due rette passanti per il suo centro, una perpendicolare ed una parallela all'ipotenusa, si può ricomporre in maniera da incorporare l'altro quadrato, e formando il quadrato sull'ipotenusa, come nella figura. Questo procedimento è legato al problema della trisezione del quadrato.

Dimostrazione di Airy

Dimostrazione di Airy

Esiste anche una dimostrazione poetica, dell'astronomo Sir George Airy, in inglese:

"I am, as you can see,
a² + b² − ab
When two triangles on me stand,
Square of hypothenuse is plann'd
But if I stand on them instead
The squares of both sides are read."

di cui una traduzione letterale è

"Come potete vedere, sono
a² + b² − ab
Quando ci sono due triangoli sopra di me
È rappresentato il quadrato dell'ipotenusa
Ma se invece sto io sopra di loro
Si leggono i quadrati dei due lati"

I versi si riferiscono alla parte bianca: i primi due triangoli sono quelli rossi, i secondi quelli blu.

Sia quella di Perigal sia quest'ultima sono puramente geometriche, ossia non richiedono alcuna definizione di operazioni aritmetiche, ma solo congruenze di aree e di segmenti.

Quadrati concentrici di Pomi

Dimostrazione con quadrati concentrici

Dimostrazione geometrica basata su due quadrati concentrici, di lati rispettivamente pari all'ipotenusa ($c$) e alla somma dei due cateti ($a+b$).

Come si vede dalla figura, tolti i quattro triangoli rettangoli (in giallo di area $(ab)/2$) al quadrato più grande, che corrisponde all'area $(a+b)^{2}$, si ottiene il quadrato più piccolo, rappresentato in bianco, che equivale invece all'area $c^{2}$.

Quindi

$(a+b)^{2}-4(ab)/2=c^{2},$

da cui risolvendo si ottiene

$a^{2}+b^{2}=c^{2}.$

Questa dimostrazione, utilizzando il passaggio algebrico del quadrato della somma di due numeri, ha una rappresentazione visiva semplice e diretta, che non richiede lo spostamento e sovrapposizione di forme come le altre dimostrazioni geometriche formulate.

Dimostrazione di Garfield

Dimostrazione di Garfield

Un'altra dimostrazione geometrica, nella cui costruzione non compare alcun quadrato, fu trovata nel 1876 da James Abraham Garfield, che in seguito divenne il ventesimo Presidente degli Stati Uniti d'America. Allora nell'esercito, Garfield commentò il suo risultato: "Pensiamo che con questa dimostrazione matematica possiamo trovare d’accordo tutti i deputati, indipendentemente dal loro credo politico". Garfield aveva avviato una spietata campagna anticorruzione che gli aveva causato l'astio di numerosi colleghi parlamentari, tanto che venne ucciso pochi mesi dopo essere eletto presidente.

La dimostrazione segue sostanzialmente il metodo usato nella dimostrazione di Pomi, applicato però a metà figura, considerando cioè il trapezio anziché il quadrato:

Consideriamo una copia del triangolo rettangolo in questione, ruotata di 90 gradi in modo da allineare i due cateti differenti (nella figura a lato il rosso ed il blu). Si uniscono poi gli estremi delle ipotenuse, ottenendo un trapezio. Uguagliando l'area del trapezio alla somma di quelle dei tre triangoli rettangoli, si dimostra il teorema.

In formule, detto $a$ il cateto rosso, $b$ il blu e $c$ l'ipotenusa, e ricordando la potenza del binomio

${\frac {(a+b)^{2}}{2}}={\frac {ab}{2}}+{\frac {ab}{2}}+{\frac {c^{2}}{2}}\,\,\Rightarrow \,\,a^{2}+b^{2}=c^{2}.$

Con i teoremi di Euclide

Dimostrazione con Euclide

Un'altra dimostrazione utilizza il primo teorema di Euclide. Si traccia l'altezza sull'ipotenusa. Questa spezza l'ipotenusa in due segmenti, di lunghezza $p$ e $q$. Il teorema di Euclide fornisce le relazioni

${\frac {a}{p}}={\frac {c}{a}},\ {\frac {b}{q}}={\frac {c}{b}},$

da cui

$a^{2}=cp,\ b^{2}=cq$

e quindi

$a^{2}+b^{2}=c(p+q)=c^{2}.$

Inverso

Vale anche l'inverso del Teorema di Pitagora (proposizione 48 del primo libro degli Elementi di Euclide): "Se in un triangolo di lati $a$, $b$ e $c$ vale la relazione $a^{2}+b^{2}=c^{2}$, allora il triangolo è rettangolo".

Dimostrazione. Sia $T$ un triangolo di lati $a$, $b$ e $c$ tale che $a^{2}+b^{2}=c^{2}$. Consideriamo un secondo triangolo rettangolo $T'$ che abbia i cateti pari ad $a$ e $b$ (è sempre possibile costruire un triangolo rettangolo dati i due cateti). Per il teorema di Pitagora (diretto) l'ipotenusa del triangolo $T'$ sarà pari a ${\sqrt {a^{2}+b^{2}}}$, ossia sarà uguale al lato $c$ del triangolo $T$. I due triangoli $T$ e $T'$ risulteranno dunque congruenti per il terzo criterio di congruenza, avendo tutti e tre i lati ordinatamente uguali. Ma allora anche il triangolo $T$ sarà rettangolo (CVD).

Un corollario del teorema di Pitagora consente di determinare se un triangolo sia o meno rettangolo, acutangolo o ottusangolo. Là dove $c$ è scelto come ipotenusa, il lato più lungo dei tre, e $a+b>c$ (altrimenti non avremo un triangolo), valgono le seguenti relazioni:

• se $a^{2}+b^{2}=c^{2},$ allora il triangolo è rettangolo;
• se $a^{2}+b^{2}>c^{2},$ allora il triangolo è acutangolo;
• se $a^{2}+b^{2}<c^{2},$ allora il triangolo è ottusangolo.

Applicazioni pratiche dell'enunciato inverso

L'enunciato inverso fornisce anche un sistema per costruire un angolo retto (o per controllare la quadratura di un angolo già esistente) in situazioni pratiche, come la topografia o l'agrimensura.

A titolo di esempio, con una fune di lunghezza pari alla somma di una terna pitagorica (diciamo 12, somma di 5, 4 e 3, in una qualche unità di misura) sarebbe sufficiente disporre le due porzioni minori della corda (quelle di misura 4 e 3) ad un certo angolo fra loro; se gli estremi della fune, disposta infine in forma triangolare, si chiudono, si saprà che l'angolo compreso fra le due porzioni minori della corda (a questo punto i due cateti) è certamente retto.

Generalizzazioni

Il teorema di Pitagora può essere generalizzato in vari modi. Solitamente, una generalizzazione è una relazione che si applica a tutti i triangoli, e che applicata ai triangoli rettangoli risulta essere equivalente al teorema di Pitagora.

Teorema del coseno

Un triangolo qualsiasi.

Una generalizzazione del teorema di Pitagora è il teorema del coseno, che si applica ad un triangolo qualsiasi (non necessariamente retto). In un triangolo con vertici e angoli indicati come in figura, vale l'uguaglianza:

${\overline {AB}}^{2}={\overline {AC}}^{2}+{\overline {BC}}^{2}-2{\overline {AC}}\cdot {\overline {BC}}\cos \gamma .$

Nel caso in cui $\gamma$ sia retto, vale $\cos \gamma =0$ e quindi l'enunciato è equivalente al teorema di Pitagora. Il termine aggiuntivo può essere interpretato come il prodotto scalare dei vettori $CA$ e $CB$.

Teorema dei seni

Il teorema dei seni mette in relazione lunghezze dei lati e angoli opposti.

Il teorema dei seni mette in relazione le lunghezze dei lati di un triangolo e i seni degli angoli opposti. Anche questa relazione si applica a qualsiasi triangolo e, nel caso in cui questo sia rettangolo, può essere ritenuta equivalente al teorema di Pitagora (benché in modo meno immediato rispetto al teorema del coseno).

Il teorema dei seni asserisce che in un triangolo qualsiasi, con le notazioni come in figura, valgono le relazioni seguenti:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.$

Elevando al quadrato:

$c^{2}=a^{2}{\frac {\sin ^{2}\gamma }{\sin ^{2}\alpha }},\quad b^{2}=a^{2}{\frac {\sin ^{2}\beta }{\sin ^{2}\alpha }}.$

Sommando i termini si ottiene:

$c^{2}+b^{2}=a^{2}{\frac {\sin ^{2}\gamma +\sin ^{2}\beta }{\sin ^{2}\alpha }}.$

Quando $\alpha$ è un angolo retto, si ottiene $\beta =\pi /2-\gamma$ e quindi

${\frac {\sin ^{2}\gamma +\sin ^{2}\beta }{\sin ^{2}\alpha }}=\sin ^{2}(\pi /2-\beta )+\sin ^{2}\beta =\cos ^{2}\beta +\sin ^{2}\beta =1.$

Si ottiene quindi in questo caso il teorema di Pitagora

$c^{2}+b^{2}=a^{2}.$

Generalizzazione che non fa uso di trigonometria

Generalizzazione del teorema di Pitagora.

È possibile estendere il teorema di Pitagora ad un triangolo qualsiasi senza fare uso di funzioni trigonometriche quali il seno ed il coseno. Dato un triangolo $ABC$ come in figura, si tracciano due segmenti che collegano il vertice $A$ con due punti $g$ e $h$ contenuti nel segmento opposto $BC$ (oppure in un suo prolungamento), in modo tale che gli angoli $AgB$ e $AhC$ siano entrambi uguali all'angolo $\alpha$ del vertice $A$. La figura mostra un caso in cui l'angolo $\alpha$ è ottuso: se è acuto, i due punti $g$ e $h$ sono in ordine inverso (il primo a destra e il secondo a sinistra) e possono uscire dal segmento $BC$.

Vale la relazione seguente:

${\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}\cdot ({\overline {Bg}}+{\overline {hC}}).$

Quando $\alpha$ è un angolo retto, i punti $g$ e $h$ coincidono e si ottiene il teorema di Pitagora

${\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}\cdot ({\overline {Bg}}+{\overline {hC}})={\overline {BC}}^{2}.$

La relazione generale può essere dimostrata sfruttando la similitudine fra i triangoli $ABC$, $gBA$ e $hAC$, che porta alle relazioni

${\frac {\overline {AB}}{\overline {BC}}}={\frac {\overline {Bg}}{\overline {AB}}},\quad {\frac {\overline {AC}}{\overline {BC}}}={\frac {\overline {hC}}{\overline {AC}}}.$

Si ottiene quindi

${\overline {AB}}^{2}={\overline {BC}}\cdot {\overline {Bg}},\quad {\overline {AC}}^{2}={\overline {BC}}\cdot {\overline {hC}}.$

Sommando le due eguaglianze si ottiene la relazione iniziale.

Generalizzazione a tutte le figure simili

Il Teorema di Pitagora continua a valere quando su ogni lato di un triangolo rettangolo si costruiscono figure simili tra loro anche non regolari. Il suo enunciato diventa:

In ogni triangolo rettangolo, l'area di un qualunque poligono, anche curvilineo, costruito sull'ipotenusa è uguale alla somma delle aree dei poligoni, simili a quello costruito sull'ipotenusa, costruiti sui cateti.

Dimostrazione

Siano:

$a$ e $b$ i cateti

$c$ l'ipotenusa

$A_{1}$ l'area del poligono costruito su $a$

$A_{2}$ l'area del poligono costruito su $b$

$A_{3}$ l'area del poligono costruito su $c.$

e

$k=a/b$ il rapporto tra i cateti

$h=c/b$ il rapporto tra l'ipotenusa e il cateto $b.$

Per il teorema di Pitagora in forma classica risulta:

$c^{2}=a^{2}+b^{2}=k^{2}b^{2}+b^{2}=b^{2}(1+k^{2}),$

e quindi

$c^{2}/b^{2}=1+k^{2}.$

Ricordando che se due poligoni simili hanno 2 lati corrispondenti in rapporto $h$ allora le loro superfici sono in rapporto $h^{2}$, avendo definito $h=c/b$ , risulta

$A_{3}=A_{2}h^{2}=A_{2}c^{2}/b^{2}=A_{2}(1+k^{2}).$

Avendo inoltre definito uguale a $k$ il rapporto tra i due cateti, per il motivo precedente risulta uguale a $k^{2}$ il rapporto tra le aree dei poligoni simili costruiti su di essi, ovvero:

$A_{1}=k^{2}A_{2}.$

Quindi:

$A_{1}+A_{2}=k^{2}A_{2}+A_{2}=(1+k^{2})A_{2}.$

E quindi

$A_{1}+A_{2}=A_{3}.$

Come volevasi dimostrare.

Negli spazi prehilbertiani

Il teorema di Pitagora può essere "generalizzato" a spazi vettoriali di qualsiasi dimensione, come lo spazio euclideo di dimensione 3 o superiore, o uno spazio vettoriale su corpo complesso, continuando a valere anche su funzioni viste come somme infinite di vettori come nell'analisi funzionale, finché sia possibile definire un prodotto scalare, rendendo lo spazio vettoriale uno spazio prehilbertiano.

La dimostrazione è semplice, e l'enunciato del teorema è: "La somma dei quadrati delle norme di due vettori ortogonali è uguale al quadrato della norma del loro vettore somma", ossia $v\perp u\Rightarrow \lVert v\rVert ^{2}+\lVert u\rVert ^{2}=\lVert v+u\rVert ^{2}.$

Dimostrazione

Per definizione di ortogonalità, il prodotto scalare fra $v$ e $u$ è nullo e commuta. L'enunciato del teorema è equivalente, per la definizione di norma euclidea, a $\langle u,u\rangle +\langle v,v\rangle =\langle u+v,u+v\rangle$. Infatti svolgendo il prodotto scalare al secondo membro, per bilinearità $\langle u+v,u+v\rangle =\langle u,u+v\rangle +\langle v,u+v\rangle =\langle u,u\rangle +\langle u,v\rangle +\langle v,u\rangle +\langle v,v\rangle$ ma $u\perp v$ quindi $\langle u,v\rangle =0=\langle v,u\rangle$ per definizione. Dunque il teorema risulta dimostrato.

Leggenda di Pitagora e delle piastrelle

Rappresentazione grafica del teorema.

Una leggenda racconta che Pitagora abbia formulato il suo teorema mentre stava aspettando un'udienza da Policrate. Seduto in un grande salone del palazzo di Samo, Pitagora si mise ad osservare le piastrelle quadrate del pavimento, si pensa che ne abbia vista una rotta perfettamente su una diagonale, così da formare due triangoli rettangoli uguali, ma oltre ad essere 2 triangoli rettangoli erano anche isosceli, avendo i due lati uguali. Pitagora immaginò un quadrato costruito sulla diagonale di rottura della piastrella, un quadrato avente come lati le diagonali delle piastrelle circostanti.

La dimostrazione è la seguente:

• l'area di ciascuna delle piastrelle adiacenti ai cateti era di: 2 mezze piastrelle (=1 piastrella);
• la somma delle due aree era quindi di: 4 mezze piastrelle (=2 piastrelle);
• l'area del quadrato costruito sull'ipotenusa (diagonale della piastrella) era di: 4 mezze piastrelle.

Dopo la conclusione, inoltre, si teorizza che Pitagora abbia fatto una ecatombe (ovvero una cerimonia sacrificale) con 100 buoi per ringraziare gli dei di averlo fatto giungere ad una risposta.

Significato esoterico del teorema

Iscrizione grafica del teorema di Pitagora ad opera dei maestri costruttori sul portale della Baugewerkeschule («Scuola Edile») a Zittau, nel sud-est della Sassonia (Germania)

Il teorema di Pitagora, in realtà, non era considerato solo una legge matematica del pensiero, ma anche una legge ontologica, cioè dell'essere, riguardante la realtà dell'uomo e del mondo. Il significato filosofico ed esoterico che esso pertanto assumeva costituiva parte integrante delle conoscenze iniziatiche riservate agli adepti della scuola pitagorica.

Una delle possibili interpretazioni del teorema che si è tramandata fino ad oggi all'interno della massoneria, dove l'emblema dei quadrati costruiti sui lati di un triangolo rettangolo compare nel gioiello indossato dagli anziani Maestri ex-Venerabili (detti in inglese Past Masters), mette in relazione la volontà del Cielo, ossia la Provvidenza, rappresentata dal cateto verticale, con la volontà della singola individualità umana, simboleggiata dal cateto orizzontale. Quanto più l'individuo, anziché estendere arbitrariamente la propria volontà, cerca di adeguarla a quella del Cielo, tanto meno subirà il peso del Destino, cioè dell'ipotenusa, e quindi tanto più riuscirà a dominare le forze della necessità che gravano sulla sua vita.

«L'equilibrio tra la Volontà e la Provvidenza da una parte, e il Destino dall'altra, era simboleggiato geometricamente dal triangolo rettangolo i cui lati sono proporzionali rispettivamente ai numeri 3, 4 e 5, triangolo al quale il Pitagorismo attribuiva una grande importanza, e che, per una coincidenza pure assai degna di nota, ne ha altrettanta nella tradizione estremo-orientale. Se la Provvidenza è rappresentata dal 3, la Volontà umana dal 4 e il Destino dal 5, in questo triangolo si ha: 3² + 4² = 5²; l'elevazione al quadrato dei numeri indica che ciò si riferisce al dominio delle forze universali, ossia propriamente al dominio animico, quello che corrisponde all'Uomo nel "macrocosmo", e al centro del quale, in quanto termine mediano, si situa la volontà nel "microcosmo".»

(René Guénon, La Grande Triade, cap. XXI, Revue de la Table Ronde, Parigi/Nancy, 1946, trad. it. in "Lettera e Spirito. Rivista di studi tradizionali", n. 36)

Bibliografia

• Carl B. Boyer, Storia della matematica, Milano, Mondadori, 1990, ISBN 978-88-04-33431-6.
• Gino Loria, Le scienze esatte nell'antica Grecia, 2ª ed., Milano, 1914.

Voci correlate

• Geometria
• Aritmogeometria
• Numero
• Radice quadrata
• Trigonometria
• Ipotenusa
• Teorema del coseno
• Identità di Parseval

Altri progetti

Altri progetti

• Wikiquote
• Wikimedia Commons

• Wikiquote contiene citazioni sul teorema di Pitagora
• Wikimedia Commons contiene immagini o altri file sul teorema di Pitagora

Collegamenti esterni

• Pitagora, teorema di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Pythagorean theorem, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Teorema di Pitagora, su MathWorld, Wolfram Research.
• (EN) Teorema di Pitagora, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (EN) Pythagoras's Theorem, in Free On-line Dictionary of Computing, Denis Howe. Disponibile con licenza GFDL
• (EN) 54 dimostrazioni del teorema di Pitagora, su faculty.umb.edu.
• Alcune animazioni grafiche di differenti dimostrazioni del teorema di Pitagora, su demonstrations.wolfram.com.
• Animazione della dimostrazione di Euclide, su walter-fendt.de. URL consultato il 16 dicembre 2004 (archiviato dall'url originale il 4 dicembre 2004).