Prodotto scalare
In matematica, in particolare nel calcolo vettoriale, il prodotto scalare è un'operazione binaria che associa ad ogni coppia di vettori appartenenti ad uno spazio vettoriale definito sul campo reale un elemento del campo.[1] Si tratta di un prodotto interno sul campo reale, ovvero una forma bilineare simmetrica definita positiva a valori reali. Essendo un prodotto puramente algebrico non può essere rappresentato graficamente come vettore unitario.
La nozione di prodotto scalare è generalizzata in algebra lineare dallo spazio euclideo ad uno spazio vettoriale qualsiasi: tale spazio può avere dimensione infinita ed essere definito su un campo arbitrario (non necessariamente quello reale). Questa generalizzazione è di fondamentale importanza ad esempio in geometria differenziale e in meccanica razionale. Aggiungendo un'ulteriore proprietà, la completezza, porta inoltre al concetto di spazio di Hilbert, per il quale la teoria si arricchisce di strumenti più sofisticati, basilari nella modellizzazione della meccanica quantistica e in molti campi dell'analisi funzionale.
Definizione[modifica | modifica wikitesto]
Si definisce prodotto scalare sullo spazio vettoriale una forma bilineare simmetrica che associa a due vettori e di uno scalare nel campo reale , generalmente indicato con o .[2]
Si tratta di un operatore binario che verifica le seguenti condizioni per , , vettori arbitrari e elemento del campo:
- Simmetria:
- Linearità rispetto al primo termine:
Diversi autori richiedono anche che la forma sia definita positiva, cioè che:[1]
per ogni diverso da zero.
Le precedenti richieste implicano anche le seguenti proprietà:
- Linearità rispetto al secondo termine:
e dal momento che un vettore moltiplicato per 0 restituisce il vettore nullo, segue che:
- .
Prodotto scalare degenere[modifica | modifica wikitesto]
Il prodotto scalare è degenere se esiste un vettore non nullo ortogonale a tutti i vettori, cioè tale che:
per ogni vettore dello spazio.
Prodotto scalare definito positivo e negativo[modifica | modifica wikitesto]
Un prodotto scalare su uno spazio vettoriale è definito positivo se:[3]
definito negativo se:
semi-definito positivo:
semi-definito negativo se:
Un prodotto scalare semi-definito positivo è (raramente) chiamato anche prodotto pseudoscalare.
Prodotto scalare nello spazio euclideo[modifica | modifica wikitesto]

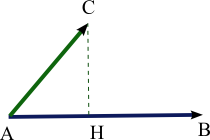

Il prodotto scalare di due vettori e del piano, applicati sullo stesso punto, è definito come:
dove e sono le lunghezze di e , e è l'angolo tra i due vettori. Il prodotto scalare si indica come , e soddisfa le proprietà algebriche di simmetria:
per ogni coppia di vettori e , e di bilinearità:
per ogni tripletta di vettori , , e per ogni numero reale . Le prime due relazioni esprimono la "linearità a destra" e le altre due "a sinistra".
Il prodotto scalare di un vettore con se stesso è sempre maggiore o uguale a zero:
Inoltre, questo è zero se e solo se il vettore è zero (proprietà di annullamento del prodotto scalare):
Questa proprietà può essere espressa affermando che il prodotto scalare è definito positivo.
Interpretazione geometrica[modifica | modifica wikitesto]
Poiché è la lunghezza della proiezione ortogonale di su se i vettori proiezione ortogonale di su e hanno stessa direzione, altrimenti è l'opposto della lunghezza, si può interpretare geometricamente il prodotto scalare come il prodotto delle lunghezze di questa proiezione e di , moltiplicato per -1 se la proiezione ortogonale di su e hanno direzione opposta. Si possono inoltre scambiare i ruoli di e , interpretare come la lunghezza (con segno definito come prima) della proiezione di su ed il prodotto scalare come il prodotto delle lunghezze di questa proiezione e della lunghezza di .
Prodotto scalare positivo, nullo e negativo[modifica | modifica wikitesto]
Il coseno di un angolo è positivo se è un angolo acuto (cioè compreso fra -90° e 90°), nullo se è un angolo retto e negativo se è un angolo ottuso. Ne segue che il prodotto scalare è:
- Positivo se , e l'angolo è acuto.
- Nullo se , oppure è retto.
- Negativo se , e l'angolo è ottuso.
I casi in cui è acuto ed ottuso sono mostrati in figura. In entrambi i casi il prodotto scalare è calcolato usando l'interpretazione geometrica, ma il segno è differente.
In particolare, valgono inoltre le proprietà seguenti:
- Se i vettori sono paralleli ed .
- Se i vettori sono ortogonali ed .
- Se i vettori sono paralleli ma orientati in verso opposto, ed .
Se e sono versori, cioè vettori di lunghezza 1, il loro prodotto scalare è semplicemente il coseno dell'angolo compreso.
Il prodotto scalare di un vettore con se stesso è il quadrato della lunghezza del vettore.
Applicazioni in fisica[modifica | modifica wikitesto]
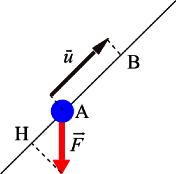
Nella fisica classica, il prodotto scalare è usato nei contesti in cui si debba calcolare la proiezione di un vettore lungo una determinata componente. Ad esempio, il lavoro compiuto da una forza costante su un corpo che si sposti in direzione è il prodotto scalare:
dei due vettori.
Applicazioni in geometria[modifica | modifica wikitesto]
Il teorema del coseno può essere formulato agevolmente usando il prodotto scalare. Dati tre punti , , qualsiasi del piano, vale la relazione seguente:
Espressione analitica[modifica | modifica wikitesto]
Il prodotto scalare è definito in geometria analitica in modo differente: si tratta della funzione che, in un qualsiasi spazio euclideo associa a due vettori e il numero:
dove denota una sommatoria.
Ad esempio, il prodotto scalare di due vettori tridimensionali [1, 3, −2] e [4, −2, −1] è [1, 3, −2]·[4, −2, −1] = 1×4 + 3×(−2) + (−2)×(−1) = 0.
In questo modo è possibile definire l'angolo compreso fra due vettori in un qualsiasi spazio euclideo, invertendo la formula data sopra, facendo cioè dipendere l'angolo dal prodotto scalare e non viceversa:
Notazioni[modifica | modifica wikitesto]
Spesso il prodotto scalare fra e si indica anche come o come . Utilizzando il prodotto tra matrici e considerando i vettori come matrici , il prodotto scalare canonico si scrive anche come:
dove è la trasposta di . L'esempio visto sopra si scrive quindi in notazione matriciale nel modo seguente:
Equivalenza fra le due definizioni[modifica | modifica wikitesto]
L'equivalenza fra le due definizioni può essere verificata facendo uso del teorema del coseno. Nella forma descritta sopra, il teorema asserisce che il prodotto scalare di due vettori e nel piano, definito in modo geometrico, è pari a:
Ponendo e ed usando il teorema di Pitagora si ottiene:
L'equivalenza in uno spazio euclideo di dimensione arbitraria può essere verificata in modo analogo.
Applicazioni[modifica | modifica wikitesto]
Il prodotto scalare riveste fondamentale importanza sia in fisica che in vari settori della matematica, ad esempio nella classificazione delle coniche, nello studio di una funzione differenziabile intorno ad un punto stazionario, delle trasformazioni del piano o nella risoluzione di alcune equazioni differenziali. Spesso in questi contesti viene fatto uso del teorema spettrale, un importante risultato connesso al prodotto scalare.
Norma di un vettore[modifica | modifica wikitesto]
Nel piano cartesiano il prodotto scalare permette di definire e trattare la nozione geometrica di lunghezza di un vettore. Tale concetto può essere esteso ad uno spazio vettoriale di dimensione arbitraria introducendo un concetto analogo: la norma. Formalmente, se ed il prodotto scalare è definito positivo, è possibile dotare lo spazio vettoriale di una norma. Più precisamente, la funzione:
soddisfa per ogni vettore , e per ogni scalare le proprietà:
- se e solo se
e dunque rende lo spazio vettoriale uno spazio normato.
Matrice associata[modifica | modifica wikitesto]
In modo analogo alla matrice associata ad una applicazione lineare, fissata una base , un prodotto scalare è identificato dalla matrice simmetrica associata , definita nel modo seguente:
D'altro canto, ogni matrice simmetrica dà luogo ad un prodotto scalare.[5] Molte proprietà del prodotto scalare e della base possono essere lette sulla matrice associata.
Fissata la matrice , per ogni coppia di vettori colonna il prodotto scalare è definito dalla legge
Dove è il vettore riga trasposto.
La matrice scritta rispetto ad una base ortonormale di un certo prodotto scalare è la matrice identità; se la base è ortogonale ma non normalizzata, invece, la matrice sarà semplicemente diagonale.
Radicale[modifica | modifica wikitesto]
Il radicale di un prodotto scalare è l'insieme dei vettori per cui:
per ogni . Il radicale è un sottospazio vettoriale di . Il prodotto scalare si dice degenere se il radicale ha dimensione maggiore di zero.
Se ha dimensione finita e è la matrice associata a rispetto ad una qualsiasi base, applicando il teorema della dimensione si trova facilmente che:
dove è il rango di e è il radicale. Quindi un prodotto scalare è non degenere se e solo se la matrice associata è invertibile. Si definisce il rango del prodotto scalare come .
Un prodotto scalare definito positivo o negativo è necessariamente non degenere. Non è vero il contrario, infatti il prodotto scalare associato rispetto alla base canonica alla matrice:
non è degenere, ma non è né definito positivo né definito negativo.
Vettori isotropi[modifica | modifica wikitesto]
Un vettore è isotropo se = 0. Tutti i vettori del radicale sono isotropi, ma possono esistere vettori isotropi che non appartengono al radicale. Ad esempio, per il prodotto scalare associato alla matrice descritta sopra il vettore è isotropo ma non è contenuto nel radicale, che ha dimensione zero.
Ortogonalità[modifica | modifica wikitesto]
Due vettori e si dicono ortogonali se . Il sottospazio ortogonale a (sottospazio vettoriale di ) è definito come:
Il sottospazio ortogonale è appunto un sottospazio vettoriale di . Contrariamente a quanto accade con il prodotto canonico nello spazio euclideo, un sottospazio ed il suo ortogonale non si intersecano in generale in un punto solo (possono addirittura coincidere). Per quanto riguarda le loro dimensioni, vale la seguente disuguaglianza:
Se il prodotto scalare è non degenere, vale l'uguaglianza
Infine, se il prodotto scalare è definito positivo o negativo, effettivamente uno spazio e il suo ortogonale si intersecano solo nell'origine e sono in somma diretta. Si ottiene:
Una base ortogonale di vettori di è una base di vettori a due a due ortogonali. Una base è ortogonale se e solo se la matrice associata al prodotto scalare rispetto a questa base è diagonale.
Trasformazione ortogonale[modifica | modifica wikitesto]
Una trasformazione ortogonale è una applicazione lineare invertibile in sé che preserva il prodotto scalare, cioè tale che:
Teorema di Sylvester[modifica | modifica wikitesto]
Se è il campo dei numeri reali e ha dimensione n, il teorema di Sylvester reale afferma che, dato un prodotto scalare su , si ha che:
- Esiste una base ortogonale di rispetto a .
- Due basi ortogonali per hanno la stessa segnatura, che dipende quindi solo da .
- Due prodotti scalari con la stessa segnatura sono isomorfi.
Quindi la matrice associata è una matrice diagonale avente sulla diagonale solo i numeri 0, 1, e -1, in ordine sparso. Siano , e rispettivamente il numero di volte che compaiono i numeri 0, 1 e -1 sulla diagonale: la terna è la segnatura del prodotto scalare.
La segnatura è un invariante completo per l'isometria: due spazi vettoriali con prodotto scalare sono isometrici se e solo se hanno la stessa segnatura.
Il teorema di Sylvester complesso dice invece che esiste sempre una base ortogonale tale che per ogni il numero è uguale a 0 oppure 1. In questo caso, il rango è un invariante completo per l'isometria: due spazi vettoriali complessi con prodotto scalare sono isometrici se e solo se hanno lo stesso rango.
Endomorfismo simmetrico[modifica | modifica wikitesto]
Un endomorfismo è simmetrico o autoaggiunto rispetto al prodotto scalare se:
per ogni coppia di vettori . Un endomorfismo è simmetrico se e solo se la matrice associata rispetto ad una qualsiasi base ortonormale è simmetrica.
Esempi[modifica | modifica wikitesto]
- Il prodotto scalare canonico fra vettori del piano o dello spazio euclideo è un prodotto scalare definito positivo.
- Sia lo spazio vettoriale delle funzioni continue sull'intervallo [0,1], a valori reali. Si può definire un prodotto scalare su ponendo:
- Questo prodotto scalare è definito positivo, perché l'integrale di è strettamente positivo se non è costantemente nulla.
- Si può definire sullo spazio vettoriale delle funzioni misurabili a valori reali lo stesso prodotto scalare del punto precedente. Qui il prodotto scalare è solo semidefinito positivo: infatti se è la funzione che vale 1 su 1/2 e 0 su tutto il resto, l'integrale di è zero ( è isotropa).
Note[modifica | modifica wikitesto]
- ^ a b Hoffman, Kunze, Pag. 271.
- ^ S. Lang, Pag. 185.
- ^ S. Lang, Pag. 151.
- ^ Questo rimane vero per una generica forma bilineare, di cui i prodotti scalari sono solo un particolare tipo.
- ^ Ciò è vero solo se si considerano prodotti scalari validi anche quelli degeneri e che non sono definiti positivi per ogni coppia di vettori non nulli.
Bibliografia[modifica | modifica wikitesto]
- Serge Lang, Algebra lineare, Torino, Bollati Boringhieri, 1992, ISBN 88-339-5035-2.
- (EN) Kenneth Hoffman, Ray Kunze, Linear Algebra, 2ª ed., Englewood Cliffs, New Jersey, Prentice - Hall, inc., 1971, ISBN 0-13-536821-9.
- (EN) Arfken, G. "Scalar or Dot Product." §1.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 13–18, 1985.
- (EN) Jeffreys, H. and Jeffreys, B. S. "Scalar Product." §2.06 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 65–67, 1988.
Voci correlate[modifica | modifica wikitesto]
- Disuguaglianza di riarrangiamento
- Forma bilineare
- Forma sesquilineare
- Prodotto vettoriale
- Prodotto misto
- Spazio euclideo
- Teorema di Sylvester
- Teoria spettrale
Altri progetti[modifica | modifica wikitesto]
 Wikibooks contiene testi o manuali sul prodotto scalare
Wikibooks contiene testi o manuali sul prodotto scalare Wikizionario contiene il lemma di dizionario «prodotto scalare»
Wikizionario contiene il lemma di dizionario «prodotto scalare» Wikimedia Commons contiene immagini o altri file sul prodotto scalare
Wikimedia Commons contiene immagini o altri file sul prodotto scalare
Collegamenti esterni[modifica | modifica wikitesto]
- prodotto scalare, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Eric W. Weisstein, Dot Product, su MathWorld, Wolfram Research.
- (EN) Inner product, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
- (EN) Explanation of dot product including with complex vectors, su mathreference.com.
- (EN) "Dot Product" by Bruce Torrence, Wolfram Demonstrations Project, 2007.
| Controllo di autorità | GND (DE) 4181619-5 |
|---|




























































![{\displaystyle \mathbf {a} =[a_{1},a_{2},\dots ,a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c061408110917f070e137303f66897749379ee8)
![{\displaystyle \mathbf {b} =[b_{1},b_{2},\dots ,b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25691ac42a0bfc234673f856faa435b135e23bde)










![{\displaystyle \mathbf {a} =[a_{1},a_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65af6c5c79fa37331659207f4147ec317f869544)
![{\displaystyle \mathbf {b} =[b_{1},b_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1194548f666164794ddc28648a193f0f7f6ec9db)























![{\displaystyle [1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a93c33bf544dd008f34d152345c97525bda7fe8)
















![{\displaystyle C([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44211c4c325ea7edb9462e7ccecda09841a41216)



![{\displaystyle M([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c41b63549f6dc497ba8efa31059d0ed62d66ace)