Matrice
In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi.
Ad esempio:
Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.
Storia[modifica | modifica wikitesto]
Tracce dell'utilizzo di matrici risalgono fino ai primi secoli a.C. Nel corso della storia più volte è capitato che matematici vissuti in epoche e luoghi diversi, durante lo studio di sistemi lineari, abbiano disposto i coefficienti del sistema in forma tabellare, fatto che evidenzia come le matrici siano una struttura particolarmente intuitiva e conveniente per questi scopi.[1] Interessanti reperti sono anche i quadrati latini e i quadrati magici. Fu solo a partire dal XVII secolo comunque che l'idea delle matrici fu ripresa e sviluppata, prima con risultati e idee ottenuti in contesti di studio specifici, poi con la loro generalizzazione. Lo sviluppo infine è continuato fino a dare alla teoria delle matrici la forma che oggi conosciamo.[1]
I primi a sfruttare le matrici per agevolare i propri calcoli furono i matematici cinesi, proprio nell'affrontare i sistemi lineari. Nel Jiuzhang Suanshu (Nove capitoli sulle arti matematiche), steso durante la dinastia Han, l'ottavo capitolo è interamente dedicato allo svolgimento di un problema matematico formulato sotto forma di sistema lineare. L'autore dispone ingegnosamente i coefficienti di ogni equazione parallelamente in senso verticale, in maniera quindi differente dalla notazione odierna, che li vuole disposti orizzontalmente, per righe: una semplice differenza di notazione.[1][2] Ai numeri così disposti si applicava una serie di operazioni portandoli in una forma tale da rendere evidente quale fosse la soluzione del sistema: è quello che oggi conosciamo come metodo di eliminazione gaussiana, scoperto in occidente solo agli inizi del XIX secolo con gli studi del matematico tedesco Carl Friedrich Gauss.[1] All'interno dello Jiuzhang Suanshu comparve anche il concetto di determinante, inteso come metodo per determinare se un sistema lineare ammette un'unica soluzione.[2]
Un'idea più moderna di determinante fece la sua comparsa nel 1683, a distanza di poco tempo sia in Giappone, con Kōwa Seki (Method of solving the dissimulated problems), che in Europa, con Leibniz. Nella prima metà del XVIII secolo, Maclaurin scrisse il Treatise of Algebra (Trattato di algebra)[3], pubblicato postumo nel 1748, nella quale mostrava il calcolo dei determinanti per matrici quadrate di ordine 2 e 3. Cramer diede il suo contributo nel 1750 presentando l'algoritmo per il calcolo del determinante per matrici quadrate di ordine qualunque, usato nel metodo oggi noto come regola di Cramer (Introduction à l'analyse des lignes courbes algébriques). Ulteriori sviluppi sul concetto di determinante furono poi apportati da Bézout (Sur le degré des équations résultantes de l'évanouissement des inconnues, 1764), Vandermonde (Mémoire sur l'élimination, 1772)[4], Laplace (1772), Lagrange (1773), Gauss (1801) che introdusse per la prima volta il termine determinante, Cauchy (1812) che usò per la prima volta il determinante nella sua concezione moderna, ottenendo anche importanti risultati sui minori e le matrici aggiunte, e Jacobi.[1] All'inizio del XIX secolo venne usato per la prima volta in occidente il metodo di eliminazione gaussiana da parte di Gauss, per lo studio dell'orbita dell'asteroide Pallas in base alle osservazioni ottenute fra il 1803 ed il 1809.[1] Altri concetti ed idee fondamentali della teoria delle matrici furono poi studiati, sempre in contesti specifici, da Cauchy, Sturm, Jacobi, Kronecker, Weierstrass e Eisenstein.
Nel 1848 il matematico e avvocato inglese Sylvester introdusse per la prima volta il termine matrice. Il suo collega avvocato Cayley introdusse nel 1853 l'inversa di una matrice.[1], e nel 1858 fornì la prima definizione astratta di matrice, in Memoir on the theory of matrices (Memorie sulla teoria delle matrici)[5], mostrando come tutti gli studi precedenti non fossero altro che casi specifici del suo concetto generale. All'interno del testo Cayley forniva inoltre un'algebra delle matrici, definendo le operazioni basilari di somma, moltiplicazione tra matrici, moltiplicazione per scalari e inversa di una matrice.[1] Ancora ignaro di tali opere, nel 1878 Frobenius pubblicò Ueber lineare Substitutionen und bilineare Formen (Sulle sostituzioni lineari e forme bilineari), nel quale riportava importanti risultati sulle matrici, quale per esempio la definizione di rango[1]. Nel 1888 il geodeta Jordan nella terza edizione del suo Handbuch der Vermessungskunde (Manuale di geodesia) ampliò il metodo di eliminazione di Gauss in quello che oggi è noto come metodo di eliminazione di Gauss-Jordan.[6] Altri contributi importanti furono dati da Bôcher nel 1907 con Introduction to higher algebra; altri testi di rilievo furono scritti da Turnbull ed Aitken negli anni trenta (The Theory of Canonical Matrices e Determinants and Matrices) e da Mirsky nel 1955 (An introduction to linear algebra).[1]
A partire dalla seconda metà del XX secolo l'avvento dei computer ha dato un'impressionante accelerazione alla diffusione delle matrici e dei metodi matriciali. Grazie ai computer infatti è stato possibile applicare in maniera efficiente metodi iterativi precedentemente ritenuti troppo onerosi, portando di conseguenza allo sviluppo di nuove tecniche per la risoluzione di importanti problemi dell'algebra lineare, quali il calcolo degli autovettori e autovalori, il calcolo dell'inversa di una matrice e la risoluzione di sistemi lineari.[7] Ciò a sua volta ha permesso l'introduzione delle matrici in altre discipline applicate, come per esempio la matematica economica e la probabilità, che grazie ad esse hanno potuto rappresentare concetti complessi in maniera più semplice. Altri campi relativamente più recenti, invece, come per esempio la ricerca operativa, hanno basato ampiamente la propria disciplina sull'utilizzo delle matrici.[7]
Definizioni e notazioni[modifica | modifica wikitesto]
Una matrice è una tabella rettangolare di numeri. Da un punto di vista formale, può essere definita come una funzione
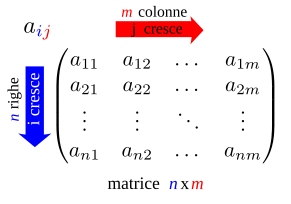
dove e sono interi positivi fissati e è un qualunque insieme fissato, come ad esempio quello dei numeri reali. Le righe orizzontali di una matrice sono chiamate righe, mentre quelle verticali colonne. Ad esempio, la matrice mostrata sopra ha due righe e tre colonne. Una matrice generica è descritta come in figura sopra oppure anche nel modo seguente (che viene considerata più proficua come notazione per il fatto di non dover differenziare nelle operazioni l'elemento dalla matrice stessa):
indicando con l'elemento posizionato alla riga -esima e nella colonna -esima.
La riga -esima viene indicata con , oppure più ambiguamente , mentre colonna -esima con , oppure più ambiguamente .
Gli elementi costituiscono la diagonale principale della matrice.
I vettori possono essere considerati matrici aventi una sola riga o una sola colonna. Una matrice con una sola riga, di dimensione , è detta matrice riga o vettore riga, mentre una matrice con una sola colonna, di dimensione , è detta matrice colonna o vettore colonna.
Di seguito sono mostrati in ordine una matrice , una matrice colonna ed una matrice riga;
Come mostrato negli esempi, i valori presenti nella matrice possono essere di vario tipo: interi, reali o anche complessi. In molti casi si suppone che i valori siano elementi di un campo fissato.
Algebra delle matrici[modifica | modifica wikitesto]
Sulle matrici si possono definire numerose operazioni che spesso dipendono anche dall'insieme in cui sono scelti i valori delle matrici. Nel resto del paragrafo supponiamo che le matrici abbiano tutte valori in uno stesso campo fissato.
Somma[modifica | modifica wikitesto]
Due matrici e , entrambe di tipo , possono essere sommate. La loro somma è definita come la matrice i cui elementi sono ottenuti sommando i corrispettivi elementi di e . Formalmente:
Per esempio:
Moltiplicazione per uno scalare[modifica | modifica wikitesto]
La moltiplicazione per uno scalare è un'operazione che, data una matrice e un numero (detto scalare), costruisce una nuova matrice , il cui elemento è ottenuto moltiplicando l'elemento corrispondente di per ; gli elementi della matrice e lo scalare in questione devono appartenere allo stesso campo. Formalmente:
Per esempio:
Prodotto[modifica | modifica wikitesto]
La moltiplicazione tra due matrici e è un'operazione più complessa delle precedenti. A differenza della somma, non avviene moltiplicando semplicemente gli elementi aventi lo stesso posto. La definizione di moltiplicazione che segue è motivata dal fatto che una matrice modellizza un'applicazione lineare, e il prodotto di matrici corrisponde alla composizione di applicazioni lineari.
La moltiplicazione è quindi definita soltanto se le matrici e sono rispettivamente di tipo e : in altre parole, il numero di colonne di deve coincidere con il numero di righe di . Il risultato è una matrice di tipo .
Ad esempio, siano e due matrici rispettivamente e : tra queste si può effettuare la moltiplicazione ed ottenere una matrice . Le stesse matrici, però, non possono essere moltiplicate nel modo , poiché le colonne di non sono tante quante le righe di .
Il prodotto di di righe e colonne e di righe e colonne è la matrice di dimensione , il cui elemento di posizione è dato dalla somma:
Quest'ultimo viene detto prodotto riga per colonna. Ad esempio:
Si osserva che moltiplicando una matrice per una si ottiene una matrice .
Prima riga:
Seconda riga:
Da cui:
A differenza dell'usuale moltiplicazione fra numeri, questa non è un'operazione commutativa, cioè è in generale diverso da , quando si possono effettuare entrambi questi prodotti.
Un caso particolare, ampiamente usato in algebra lineare per rappresentare le trasformazioni lineari (come rotazioni e riflessioni) è il prodotto tra una matrice ed un vettore colonna , che viene chiamato anche prodotto matrice-vettore.
Proprietà[modifica | modifica wikitesto]
Le operazioni di somma e prodotto di matrici soddisfano tutte le proprietà usuali della somma e del prodotto di numeri, ad eccezione, nel caso del prodotto di matrici, della proprietà commutativa.
Sia la matrice nulla, fatta di soli zeri (e della stessa taglia di ). Sia inoltre la matrice ottenuta moltiplicando per lo scalare . Valgono le relazioni seguenti, per ogni matrici e, per ogni numeri reali.
Proprietà della somma e del prodotto per uno scalare[modifica | modifica wikitesto]
- (la matrice nulla è l'elemento neutro della somma);
- (esistenza di un opposto per la somma);
- (proprietà associativa della somma);
- (proprietà commutativa della somma);
- (1 è l'elemento neutro del prodotto per uno scalare);
- (proprietà associativa del prodotto per uno scalare);
- (proprietà distributiva del prodotto per uno scalare rispetto alla somma).
Le prime 4 proprietà affermano che le matrici formano un gruppo abeliano rispetto all'operazione di somma. Come mostrato sopra, il prodotto non è commutativo in generale.
Proprietà del prodotto fra matrici[modifica | modifica wikitesto]
- (proprietà associativa del prodotto);
- (proprietà distributiva del prodotto rispetto alla somma).
Altre operazioni[modifica | modifica wikitesto]
Sulle matrici sono definite numerose altre operazioni. Tra queste:
- trasposizione di una matrice;
- somma diretta;
- prodotto diretto (o di Kronecker);
- matrice esponenziale;
- inversione di una matrice invertibile;
- diagonalizzazione di una matrice diagonalizzabile.
Applicazioni lineari[modifica | modifica wikitesto]
Le matrici permettono di rappresentare le trasformazioni lineari fra spazi vettoriali. Ad ogni operatore lineare da uno spazio vettoriale di dimensione a uno spazio vettoriale di dimensione si associa, per ogni possibile scelta di una coppia di basi e , la matrice tale che:
Questa matrice rappresenta l'applicazione nelle basi scelte. Molte operazioni fra matrici si traducono in operazioni fra applicazioni lineari:
- l'immagine di un vettore corrisponde alla moltiplicazione matrice-vettore;
- la somma di applicazioni (quando possibile) corrisponde alla somma fra matrici;
- la composizione di applicazioni lineari (quando possibile) corrisponde al prodotto fra matrici.
Sistemi lineari[modifica | modifica wikitesto]
Le matrici sono utili soprattutto a rappresentare sistemi di equazioni lineari. Il sistema:
può essere rappresentato con il suo equivalente matriciale, tramite il prodotto matrice-vettore:
Matrici quadrate[modifica | modifica wikitesto]
Fra le matrici, occupano un posto di rilievo le matrici quadrate, cioè le matrici , che hanno lo stesso numero di righe e di colonne. Una matrice quadrata ha una diagonale principale, quella formata da tutti gli elementi con indici uguali. La somma di questi elementi è chiamata traccia. L'operazione di trasposizione trasforma una matrice quadrata nella matrice ottenuta scambiando ogni con , in altre parole ribaltando la matrice intorno alla sua diagonale principale.
Una matrice tale che è una matrice simmetrica. In altre parole, è simmetrica se . Se tutti gli elementi che non stanno nella diagonale principale sono nulli, la matrice è detta diagonale.
Prodotto di matrici quadrate[modifica | modifica wikitesto]
Tra le più importanti matrici vi è la matrice identità : si tratta di una matrice avente 1 su ogni elemento della diagonale e 0 altrove. La matrice è importante perché rappresenta l'elemento neutro rispetto al prodotto: infatti le matrici possono essere moltiplicate fra loro, e vale (oltre a quelle scritte sopra) la proprietà seguente per ogni :
ossia è l'elemento neutro del prodotto. Nello spazio delle matrici sono quindi definiti una somma e un prodotto, e le proprietà elencate fin qui asseriscono che l'insieme è un anello, simile all'anello dei numeri interi, con l'unica differenza che il prodotto di matrici non è commutativo.
Determinante[modifica | modifica wikitesto]
Un'importante quantità definita a partire da una matrice quadrata è il suo determinante. Indicato con , questo numero fornisce molte informazioni essenziali sulla matrice. Ad esempio, determina se la matrice è invertibile, cioè se esiste una matrice tale che:
Il determinante è l'ingrediente fondamentale della regola di Cramer, utile a risolvere alcuni sistemi lineari.
Polinomio caratteristico, autovettori, diagonalizzabilità[modifica | modifica wikitesto]
La traccia e il determinante possono essere racchiuse in un oggetto ancora più raffinato, di fondamentale importanza nello studio delle trasformazioni lineari: il polinomio caratteristico, un polinomio le cui radici sono gli autovalori della matrice. La conoscenza di autovalori e autovettori consente ad esempio di studiare la similitudine fra matrici, in particolare la similitudine ad una matrice diagonale.
Classi di matrici reali e complesse[modifica | modifica wikitesto]
Oltre alle matrici diagonali e simmetriche già introdotte, vi sono altre categorie di matrici importanti.
- Le matrici antisimmetriche, in cui i valori nelle caselle in posizioni simmetriche rispetto alla diagonale principale sono opposti: .
- Le matrici hermitiane (o auto-aggiunte), in cui i valori nelle caselle di posizioni simmetriche rispetto alla diagonale principale sono complessi coniugati: .
- Un quadrato magico è una matrice quadrata in cui la somma dei valori su ogni riga, colonna o diagonale è sempre la stessa.
- Le matrici di Toeplitz hanno valori costanti sulle diagonali parallele alla principale:
- Le matrici stocastiche sono matrici quadrate le cui colonne sono vettori di probabilità, cioè sequenze di reali compresi tra 0 e 1 con somma uguale a 1; esse sono usate per definire le catene di Markov.
Spazio di matrici[modifica | modifica wikitesto]
Lo spazio di tutte le matrici a valori in un fissato campo è indicato generalmente con o . Per quanto già visto, questo spazio è un gruppo abeliano con la somma. Considerato anche con la moltiplicazione per scalare, l'insieme ha una struttura di spazio vettoriale su .
Questo spazio ha una base canonica, composta da tutte le matrici aventi valore 1 sulla casella di posto e zero in tutte le altre. La base consta di elementi, e quindi lo spazio ha dimensione .
Algebra su campo[modifica | modifica wikitesto]
Nel caso delle matrici quadrate, è definito anche il prodotto. Con questa ulteriore operazione, lo spazio , indicato anche con , eredita una struttura di anello con unità. Tale struttura è compatibile con quella di spazio vettoriale definita sopra, e fornisce quindi un esempio basilare di algebra su campo.
Generalizzazioni[modifica | modifica wikitesto]
Una matrice infinita può essere definita come una successione di elementi , indicizzati da coppie di numeri naturali , senza nessun limite superiore per entrambi.
Più in generale, una generalizzazione del concetto di matrice è costruita prendendo due insiemi di indici qualsiasi (parametrizzanti le "righe" e le "colonne") e definendo una matrice come un'applicazione:
a valori in un altro dato insieme . La matrice usuale corrisponde al caso in cui e , e è ad esempio l'insieme dei numeri reali o complessi.
Questa definizione generale si serve solo di nozioni insiemistiche e non ricorre a nozioni visive e intuitive come quella di schieramento rettangolare. Consente di trattare casi molto generali: ad esempio matrici le cui righe e colonne sono etichettate da indici in un qualunque sottoinsieme degli interi , matrici etichettate da coppie o in generale da -uple di interi come quelle che si incontrano nella meccanica quantistica o nella chimica molecolare, matrici infinite etichettate con gli insiemi e come quelle che permettono di rappresentare successioni polinomiali o serie formali con due variabili.
Per poter definire somma, prodotto e altre operazioni sulle matrici, è opportuno che l'insieme sia dotato di tali operazioni, ad esempio che sia un anello.
Funzione di matrice[modifica | modifica wikitesto]
La teoria delle funzioni di matrice è di grande interesse per lo studio dei sistemi differenziali: in generale la funzione di una matrice non coincide con la matrice delle funzioni dei suoi elementi, ma si dimostra sfruttando il teorema di Hamilton-Cayley che ciascun suo elemento è una combinazione lineare di queste ultime.
Note[modifica | modifica wikitesto]
- ^ a b c d e f g h i j (EN) Storia dell'uso delle matrici e dei determinanti su MacTutor
- ^ a b (EN) Il Nove capitoli sulle arti matematiche su MacTutor
- ^ Il testo è consultabile on-line: Treatise of Algebra.
- ^ (EN) Biografia di Vandermonde su MacTutor
- ^ L'abstract del testo è consultabile on-line: Memoir on the theory of matrices in Proceedings of the Royal Society of London, Volume 9.
- ^ S. C. Althoen and R. McLaughlin, "Gauss-Jordan Reduction: A Brief History," American Mathematical Monthly, 94:130–142 (1987).
- ^ a b Bronson 1989, Preface.
Bibliografia[modifica | modifica wikitesto]
- (EN) Richard Bronson, Schaum's Outline of Theory and Problems of Matrix Operations, New York, McGraw-Hill, 1989, pp. 230 pagine., ISBN 0-07-007978-1.
- Fulvio Bisi, Francesco Bonsante e Sonia Brivio, 3, in Lezioni di algebra lineare con applicazioni alla geometria analitica, Pavia, La Dotta, agosto 2013, ISBN 88-98648-02-2.
- (EN) David M. Burton, The History of Mathematics: An Introduction, 6ª edizione, McGraw-Hill, 1º dicembre 2005, ISBN 978-0-07-110635-1.
- (EN) Richard W. Jr. Feldmann, Arthur Cayley - Founder of Matrix Theory, The Mathematics Teacher, 55, 1962, Pagine 482-484..
- (EN) Gene H. Golub, Charles F. Van Loan, Matrix computations, 3ª edizione, Johns Hopkins University Press, 1996, ISBN 0-8018-5414-8.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «matrice»
Wikizionario contiene il lemma di dizionario «matrice» Wikiversità contiene risorse sulla matrice
Wikiversità contiene risorse sulla matrice Wikimedia Commons contiene immagini o altri file sulla matrice
Wikimedia Commons contiene immagini o altri file sulla matrice
Collegamenti esterni[modifica | modifica wikitesto]
- matrice, su sapere.it, De Agostini.
- matrice, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) matrix, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Matrice, su MathWorld, Wolfram Research.
- (IT) Calcolatrice per matrici e vettori online
- (EN) Storia dell'uso delle matrici e dei determinanti su MacTutor
- (EN) Matrice Archiviato il 15 giugno 2010 in Internet Archive. su PlanetMath
| Controllo di autorità | Thesaurus BNCF 17734 · LCCN (EN) sh85082210 · GND (DE) 4037968-1 · BNE (ES) XX529678 (data) · BNF (FR) cb119324420 (data) · J9U (EN, HE) 987007557992905171 |
|---|






![{\displaystyle A={\begin{pmatrix}\;[A]_{1,1}&[A]_{1,2}&\cdots &[A]_{1,n}\\\;[A]_{2,1}&[A]_{2,2}&\cdots &[A]_{2,n}\\\vdots &\vdots &\ddots &\vdots \\\;[A]_{m,1}&[A]_{m,2}&\cdots &[A]_{m,n}\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f25fe31f3586dc651fc298ce42b6c527a3304a02)
![{\displaystyle [A]_{i,j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b112d2151a8c1e6f631983e20f07d52e80f6be)






![{\displaystyle [A]_{i,i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f9947cb832d93bec91a5492bb8846b870bc5dc)







![{\displaystyle [A+B]_{i,j}:=[A]_{i,j}+[B]_{i,j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/618ebc3a577e9f52039846a9003cb5c8d63e16e1)



![{\displaystyle [cA]_{ij}:=c[A]_{i,j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfba89f5d8c48e3ce8b3cc3433d23e365dc3e8a9)












![{\displaystyle [C]_{i,j}=Row_{i}(A)\times Col_{j}(B)=[A]_{i,1}[B]_{1,j}+[A]_{i,2}[B]_{2,j}+\cdots +[A]_{i,p}[B]_{p,j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f9f7acbf171132aeb3d64ec162e049f9e888920)

![{\displaystyle C=AB={\begin{pmatrix}1&1&2\\0&1&-3\end{pmatrix}}{\begin{pmatrix}1&1&1\\2&5&1\\0&-2&1\end{pmatrix}}={\begin{pmatrix}\,\![C]_{1,1}&[C]_{1,2}&[C]_{1,3}\\\,\![C]_{2,1}&[C]_{2,2}&[C]_{2,3}\end{pmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6edd5f6ca7079fbf1636dde3444bf3bf2185bcbd)


![{\displaystyle \![C]_{1,1}=(1\cdot 1)+(1\cdot 2)+(2\cdot 0)=3;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/701c5b4797380b99274785a83a64c1a56d39e422)
![{\displaystyle [C]_{1,2}=(1\cdot 1)+(1\cdot 5)+(2\cdot (-2))=2;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c62d8a09a4ba3f308a1ce71800ffe8be1caaa610)
![{\displaystyle [C]_{1,3}=(1\cdot 1)+(1\cdot 1)+(2\cdot 1)=4.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07731fa772db96ed35c3f16bf6a933d41e4c5e68)
![{\displaystyle [C]_{2,1}=(0\cdot 1)+(1\cdot 2)+(-3\cdot 0)=2;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15a80c2ffcdde0ab55174e5fb5e434789270bb7d)
![{\displaystyle [C]_{2,2}=(0\cdot 1)+(1\cdot 5)+(-3\cdot (-2))=11;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f7c7afbb3d524d841be16f51a3f353356fd85b)
![{\displaystyle [C]_{2,3}=(0\cdot 1)+(1\cdot 1)+(-3\cdot 1)=-2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6e3a3024967ae397bf6bada711d0736d1d627d4)
![{\displaystyle C={\begin{pmatrix}\,\![C]_{1,1}&[C]_{1,2}&[C]_{1,3}\\\,\![C]_{2,1}&[C]_{2,2}&[C]_{2,3}\end{pmatrix}}={\begin{pmatrix}3&2&4\\2&11&-2\end{pmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47d3db85ae6e75acccc8c7a77990c9dcaeeae652)























![{\displaystyle T(v_{i})=\sum _{j=1}^{n}[A]_{i,j}w_{j},\quad \forall i\in \{1,2,\ldots ,m\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7514b8b6ab7b6fa7e6675a00c66beeae11dc1020)
































