Algebra di Boole
L'algebra di Boole (anche detta algebra booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0.
Storia[modifica | modifica wikitesto]
Ideata nel 1847 all'University College Cork da George Boole nel suo libro The Mathematical Analysis of Logic per scrivere in forma algebrica la logica proposizionale e da lui ulteriormente sviluppata nel 1854 in An Investigation of the Laws of Thought, l'algebra di Boole è stata fondamentale nel campo dell'elettronica digitale, dove nella progettazione dei circuiti elettronici rivestono grande importanza i teoremi deducibili dagli assiomi che fondano l'algebra, come il teorema di Shannon del 1940 che mostra come scomporre una funzione booleana complessa in funzioni più semplici, o per ottenere un'espressione canonica da una tabella della verità. L'algebra di Boole riveste un ruolo di fondamentale importanza nell'informatica, tanto che ogni linguaggio di programmazione moderno definisce al suo interno gli operatori logici; è usata inoltre anche nella teoria degli insiemi e nella probabilità.
Descrizione[modifica | modifica wikitesto]
Le operazioni fondamentali non sono addizione e sottrazione ma gli operatori logici: la congiunzione o prodotto logico indicata con ∧ oppure AND; la disgiunzione o somma logica indicata con ∨ oppure OR; la negazione o complementazione indicata con ¬ oppure NOT. Con tale formalismo si possono descrivere le relazioni logiche in modo simile a quanto fa l'algebra ordinaria con le relazioni numeriche: la combinazione di AND, OR e NOT permette di sviluppare qualsiasi funzione booleana e i tre operatori logici formano pertanto un insieme funzionalmente completo.
Definizione formale[modifica | modifica wikitesto]
Matematicamente, si dice algebra di Boole un qualunque reticolo dotato di proprietà, quali la distributività, l'esistenza di minimo e massimo e l'esistenza del complemento: l'algebra booleana risulta criptomorfa, cioè associata biunivocamente e in modo da risultare logicamente equivalente a un insieme parzialmente ordinato reticolato. D'altra parte, ogni algebra booleana risulta criptomorfa a un particolare tipo di anello, chiamato anello booleano. La struttura può essere specificata attraverso gruppi e anelli o attraverso i reticoli in modo del tutto equivalente.
Più precisamente, si parla di algebra di Boole in riferimento a un insieme K sul quale sono definite le operazioni di somma logica (+, OR) e prodotto logico (*, AND), cioè una terna , che costituisce un reticolo in cui sono inoltre soddisfatte la proprietà distributiva, l'esistenza del minimo e del massimo e l'esistenza del complemento.
Nel dettaglio, si ha un'algebra di Boole quando su sono soddisfatte le seguenti proprietà:
- Commutativa
- Associativa
- Assorbimento
- Distributiva
Idempotenza
- Esistenza di minimo e massimo
- Esistenza del complemento
Il modo in cui sono elencate le proprietà vuole mettere in evidenza la simmetria che c'è tra i due operatori, che è poi all'origine della legge di dualità e altre proprietà molto importanti. Nell'elencare gli assiomi, il complemento è stato indicato con un trattino sulla variabile (che è tipograficamente difficile da realizzare, anche se è la notazione migliore); il complemento può anche essere indicato con un "!" (punto esclamativo) antecedente alla variabile booleana (notazione tipica della programmazione in C e C++), con uno slash prima della variabile o addirittura con un segno meno antecedente a essa, quando non è una notazione equivoca. Il complemento corrisponde all'operazione logica NOT.
Un'ultima osservazione riguarda il fatto che le prime 4 proprietà riguardano i reticoli in generale, mentre le restanti sono proprie dell'algebra di Boole, che sarà quindi indicata con la sestupla . Data la formulazione generale, da questo momento in poi ci si riferisce all'algebra primordiale, che considera , cioè l'insieme su cui si basa l'algebra di Boole è composto solamente dal minimo e dal massimo.
Si elencano ora la legge di dualità e alcune proprietà derivanti dagli assiomi ora visti con le relative dimostrazioni; oltre a queste conseguenze, ci sono poi due importanti teoremi dell'algebra booleana che sono i teoremi di De Morgan e il teorema di Shannon. I teoremi che si dimostrano ora sono validi per qualsiasi "porzione di realtà" che soddisfa gli assiomi di quest'algebra astratta e, in particolare, saranno applicabili nell'algebra degli insiemi, nell'algebra della logica delle proposizioni e nell'algebra dei circuiti.
Legge di dualità[modifica | modifica wikitesto]
Da qualsiasi identità booleana se ne può trarre un'altra per dualità, sostituendo cioè a ogni operatore e agli elementi 0 e 1 il rispettivo duale: il duale di + è *, il duale di 0 è 1 (la dimostrazione di questo sta al prossimo paragrafo), il duale di a è in generale !a (a negato, NOT a).
Grazie a questa legge, si può vedere come i 14 postulati dati per definire l'algebra booleana non sono tutti indipendenti tra loro: in particolare, si vede che PX e PX' (per X=1,...,7) sono uno il duale dell'altro.
Complementi di 0 e 1[modifica | modifica wikitesto]
0 e 1 sono uno il complementare dell'altro: per dimostrarlo basta verificare la definizione di complemento, cioè che
Si vede immediatamente che
applicando rispettivamente la proprietà del minimo e quella del massimo e il teorema ora enunciato risulta così dimostrato.
Si nota che, per come è strutturata quest'algebra, questa dimostrazione ha permesso di dimostrare a partire dagli assiomi che l'elemento neutro esiste ed è unico (l'esistenza non è quindi postulata e l'unicità è insita nell'esistenza essendo solo 2 i valori con cui sta lavorando, cosa non vera per altri tipi di algebra e altre strutture algebriche).
Convoluzione[modifica | modifica wikitesto]
Negando due volte lo stesso elemento, si ottiene l'elemento stesso (logica aristotelica: una doppia negazione corrisponde a un'affermazione).
Per dimostrarlo, basta considerare l'assioma di esistenza del complemento considerato su due elementi a e b=!a:
Essendo valida la proprietà commutativa e siccome il complemento esiste unico, se ne deduce facilmente che , che è quello che si voleva dimostrare.
Elementi neutri[modifica | modifica wikitesto]
0 è l'elemento neutro della somma (disgiunzione logica, ∨, OR) e 1 è l'elemento neutro del prodotto (congiunzione logica, ∧, AND).
Per la dimostrazione, basta sfruttare la proprietà dell'assorbimento grazie alla quale si deduce che:
Ora, sfruttando la proprietà del massimo e minimo per la quale a*0=0 e a+1=1, si deduce facilmente che:
che è quello che si doveva dimostrare.
Assorbimento del complemento (secondo teorema dell'assorbimento)[modifica | modifica wikitesto]
L'assorbimento del complemento dice che
Per dimostrarlo, basta applicare la proprietà distributiva secondo la quale:
dopodiché, notando che a+!a=1 e che 1 è l'elemento neutro del prodotto logico risulta dimostrato il teorema.
Per la legge di dualità si capisce anche che esiste un teorema duale a questo che sarà:
Questo teorema può essere preso per vero accettando la validità della legge di dualità, oppure può essere dimostrato in modo del tutto analogo al precedente. Si nota che, nello scrivere l'espressione duale, si è dovuta rispettare la precedenza di applicazione delle operazioni e perciò le parentesi intorno ad a+!b della seconda espressione sono necessarie.
Teorema dell'elemento unico[modifica | modifica wikitesto]
Se e , allora y è unico (o anche x è unico perché si vede che, essendo valida la proprietà commutativa, il ruolo di x e y nelle espressioni è lo stesso).
Per la dimostrazione, si suppone per assurdo che esistano due valori distinti y e z che soddisfano le due espressioni, e cioè
Essendo anche che
si è ottenuto che
Nell'ultimo passaggio, si è sfruttato il principio di equivalenza delle eguaglianze e non si è semplificato la x, cosa che non è stata dimostrata e non può essere dimostrata in quest'algebra. Allora, quello che si ha ora è che
Moltiplicando membro a membro e utilizzando la proprietà distributiva, si ha:
cioè y=z e perciò l'elemento che soddisfa le due relazioni scritte sopra è unico.
Principio di eliminazione[modifica | modifica wikitesto]
Come si è accennato prima, nell'algebra di Boole non valgono i principi di eliminazione, cioè non vale che:
Vale che y=z solamente se queste due espressioni ora scritte valgono contemporaneamente.
L'unica cosa che si può dire invece nel caso in cui valga solo la prima espressione è che:
Funzioni booleane[modifica | modifica wikitesto]
L'algebra di Boole è la trattazione dell'algebra universale a due stati e dei modelli di tale teoria, detti algebre booleane. L'algebra universale si occupa di studiare la famiglia di operazioni su un insieme, detto insieme fondamentale della famiglia algebrica e, nel caso della struttura algebrica booleana, questo contiene i soli valori 0 e 1. In pratica le algebre booleane si occupano della trattazione delle funzioni booleane di cui ora si accennano le nozioni principali: lo studio di queste funzioni è fondamentale oggi per lo studio di circuiti e reti logiche, perciò se ne possono vedere subito gli scopi pratici, ma l'importanza di queste strutture algebriche non si limita solo a questo perché è anche fondamentale nello studio delle proposizioni e dell'insiemistica, che sono argomenti un po' più astratti ma altrettanto validi e importanti.
Il numero degli argomenti che richiede un'operazione definita sull'insieme fondamentale è detto arietà (un'addizione ad esempio è un'operazione di arietà 2, anche detta operazione binaria): un'operazione su {0,1} di arietà n può essere applicata a ognuno dei 2n possibili valori dei suoi n argomenti (cioè basta calcolare le disposizioni di 2 elementi su n posti), ad esempio se si ha un'operazione di arietà 3, dato che K={0,1}, gli argomenti possibili sono 000,001,010,011,100,101,110,111 che sono 8.
Per ogni scelta di argomenti l'operazione può produrre i soli risultati 0 e 1 e per questo ci sono 22n operazioni di n argomenti: questo numero corrisponde quindi al numero totale di funzioni possibili di n variabili nell'algebra booleana.
L'algebra a due stati possiede 2 operazioni con nessun argomento (220) che restituiscono i valori 0 e 1 senza considerare nessun argomento, e 4 operazioni con un solo argomento(221): le operazioni possibili sono due (21), l'identità e la negazione e perciò in totale le operazioni sono 4 in quanto si ha 0→0 (id.), 0→1 (neg.), 1→0 (neg.), 1→1 (id.). Vi sono poi 16 operazioni binarie, 256 operazioni ternarie, 65.536 operazioni quaternarie e così via.
Siccome l'algebra di cui sta parlando è fondata su un insieme finito, una funzione può essere rappresentata oltre che in forma algebrica (cioè composizione di AND, OR e NOT), in forma tabellare, cioè con una tabella in cui a ogni composizione delle variabili "di input" (usando una terminologia più informatica) si fa corrispondere l'uscita (o anche le uscite): tutte le funzioni, anche di altre algebre, possono in teoria essere rappresentate tramite tabelle ma se l'insieme su cui è fondata l'algebra è infinito (ad esempio l'insieme dei numeri reali) non è un modo comodo per studiare la funzione; per l'algebra booleana usare le tabelle è un modo utile per studiare le funzioni e ad esempio permette facilmente la costruzione di circuiti e reti logiche nelle applicazioni elettroniche. Un esempio di tabelle si ha considerando operazioni binarie che si è già visto essere 16:
| A | B | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Una famiglia, detta anche indice, è indicizzata da un insieme di indici, che nel caso di una famiglia di operazioni costituenti un'algebra sono detti simboli dell'operazione e costituiscono il linguaggio dell'algebra in oggetto. L'operazione indicizzata da un dato simbolo è detta interpretazione di tale simbolo, e ogni simbolo definisce il numero univoco di argomenti delle rispettive interpretazioni possibili. Nel caso considerato vi è una corrispondenza biunivoca tra simbolo e interpretazione. L'algebra di Boole ha tanti simboli quante sono le operazioni possibili detti simboli di operazione booleana, anche se poche operazioni hanno simboli convenzionali, quali ! per la negazione, + per la congiunzione e * per la disgiunzione. In generale si indica con nfi l'i-esimo simbolo di n argomenti. Nell'ultimo esempio considerato invece si dà un simbolo per ognuna delle 16 funzioni possibili o anche è possibile esprimere ogni funzione come opportuna combinazione dei simboli convenzionali fondamentali, cioè AND (*), OR (+) e NOT (!).
Funzione duale[modifica | modifica wikitesto]
Data una funzione in qualsiasi forma si definisce funzione duale di e si indica con una funzione che ha per forma la forma duale di , ad esempio:
La forma duale deve rispettare le precedenze di applicazione dell'operazione della forma di partenza, per questo motivo, laddove non c'erano delle parentesi perché la AND ha precedenza sulla OR, nel momento in cui la AND diventa OR e la OR diventa AND, può esserci bisogno di parentesi.
Un'altra osservazione molto importante è che le variabili, e non le costanti 0 e 1, possono anche non essere negate perché comunque la variabile dovrà assumere tutti i valori possibili e perciò, che ci sia o meno la negazione, la funzione non cambia: nel caso visto prima allora la funzione duale può anche essere scritta come
dove si nota che la costante è stata negata. Questa osservazione può essere importante nel momento in cui si va a progettare una rete logica perché significa risparmiare porte NOT, o anche in generale, nell'espressione algebrica è sempre utile avere operazioni in meno da fare.
Basi[modifica | modifica wikitesto]
Un insieme funzionalmente completo è un insieme di operazioni la cui composizione permette di ottenere tutte le operazioni appartenenti all'algebra e a volte ci si riferisce a questi con il termine base, usato in accezione diversa rispetto alle basi di spazi vettoriali. Le tre principali basi usate nell'algebra booleana sono:
- Il reticolo, una base logica introdotta nel XIX secolo da George Boole, Charles Sanders Peirce e altri matematici che cercavano una formalizzazione algebrica dei processi logici.
- L'anello booleano, una base (non aritmetica) introdotta nel XX secolo da Ivan Ivanovič Žegalkin e Marshall Stone che proviene dall'algebra astratta.
- La base NAND, originata dal fatto che tramite l'operazione di NAND è possibile ottenere tutte le operazioni sull'insieme {0,1}. Tale base è utilizzata in particolare nella configurazione dei circuiti logici in elettronica digitale.
Gli elementi comuni a reticolo e anello sono le costanti 0 e 1 e un'operazione binaria associativa e commutativa, che nella base del reticolo è detta incontro, dal termine inglese meet, e denotata tra due elementi x e y dal simbolo x∧y, mentre nella base dell'anello è detta moltiplicazione e denotata xy. La base del reticolo ha inoltre le operazioni algebriche di unione x∨y e complemento ¬x, mentre la base dell'anello ha l'ulteriore operazione (non aritmetica) di addizione x⊕y o x+y.
Reticolo[modifica | modifica wikitesto]
Nella base del reticolo a un'algebra booleana (A, , ) si associa un insieme parzialmente ordinato (A, ), definendo:
che è anche equivalente a
È possibile anche associare un'algebra booleana a un reticolo distributivo (A, ), considerato come insieme parzialmente ordinato, dotato di elemento minimo 0 e di elemento massimo 1, in cui ogni elemento x ha un complementare tale che
e
Qui e sono usati per denotare l'inf e il sup di due elementi. Se i complementi esistono, allora sono unici.
Anello[modifica | modifica wikitesto]
La base dell'anello della generica algebra booleana (A, , ) è definita come (A, +, *), definendo a + b := (a b) ( b a ). In tale anello l'elemento neutro per la somma coincide con lo 0 dell'algebra booleana, mentre l'elemento neutro della moltiplicazione è l'elemento 1 dell'algebra booleana. Questo anello ha la proprietà che a * a = a per ogni a in A; gli anelli con questa proprietà sono chiamati anelli booleani.
Viceversa, assegnato un anello booleano A, esso può essere trasformato in un'algebra booleana definendo x y = x + y − x y e x y = x y. Poiché queste due operazioni sono l'una l'inversa dell'altra, si può affermare che ogni anello booleano è criptomorfo di un'algebra booleana e viceversa. Inoltre, una funzione f : A B è un omomorfismo tra algebre booleane se e soltanto se è un omomorfismo tra anelli booleani. La categoria degli anelli booleani e delle algebre booleane sono equivalenti.
Un anello ideale dell'algebra booleana A è un sottoinsieme I tale che per ogni x, y in I si ha x y in I e per ogni a in A a x in I. Questa nozione di ideale coincide con la nozione di anello ideale negli anelli booleani. Un ideale I di A è detto primo se I A e se a b in I implica sempre a in I o b in I. Un ideale I di A è detto massimale se I A e se l'unico ideale proprio contenente I è A stesso. Questa notazione coincide con la notazione teorica dell'ideale primo e ideale massimale nell'anello booleano A.
Il duale di un ideale è un filtro. Un filtro dell'algebra booleana A è un sottoinsieme F tale che per ogni x, y in F si ha x y in F e per ogni a in A se a x = a allora a è in F.
L'operazione di complementazione * applicata ai sottoinsiemi manda dunque gli ideali in filtri e viceversa: se B è un'algebra booleana e un suo ideale (proprio), allora è il filtro (proprio) duale di I. Se invece è un filtro (proprio), l'ideale (proprio) duale di F.
Sheffer stroke[modifica | modifica wikitesto]
La base Sheffer stroke o NAND si basa sulle operazioni NOT e AND, tramite le quali è possibile ottenere tutte le operazioni booleane. Un'algebra booleana può essere definita sia da NOT e AND sia da NOT e OR, essendo possibile definire OR attraverso NOT e AND così come AND attraverso NOT e OR:
La collezione di tutti i sottoinsiemi di un dato insieme, ovvero l'insieme delle parti o insieme ambiente, munita delle operazioni di unione, intersezione e complementazione di insiemi, che giocano rispettivamente il ruolo di OR, AND e NOT, costituisce un'algebra booleana.
Più formalmente, se B è un insieme formato da almeno 2 elementi, l'algebra booleana avente B come supporto è la struttura algebrica costituita da B, da due operazioni binarie su B, OR e AND, da un'operazione unaria NOT su B e dall'elemento 0 di B, i quali godono delle seguenti proprietà:
- Simmetria di AND:
- Simmetria di OR:
- Involuzione di NOT:
- Leggi di De Morgan:
L'insieme B è inoltre limitato inferiormente, essendo:
L'elemento 1 è definito come la negazione, o il complementare, dello 0: 1 := NOT(0). L'insieme B è dunque limitato superiormente, essendo:
e in particolare
- 0 AND 1 = 0 ; 0 OR 1 = 1
Si definisce inoltre, come operazione derivata dalle precedenti, l'operatore binario OR esclusivo, denotato XOR:
In questa algebra all'operatore XOR corrisponde la differenza simmetrica:
In elettronica la porta logica NAND è costituita da n ingressi e un'uscita che si porta a livello 0 solo se gli n ingressi si portano a livello 1. È corrispondente alla connessione in serie di una porta AND e di una NOT.
Operatori booleani[modifica | modifica wikitesto]
Si è visto che gli operatori dell'algebra booleana possono essere rappresentati in vari modi, ma spesso sono scritti semplicemente come AND, OR e NOT che è la scrittura che utilizziamo ora per parlare degli operatori booleani. Nella descrizione dei circuiti, possono anche essere usati NAND (NOT AND), NOR (NOT OR), XOR (OR esclusivo) e XNOR (NOT OR esclusivo).
Le diverse simbologie per rappresentare gli operatori sono scelte in base al campo in cui si lavora: i matematici usano spesso il simbolo + per l'OR, e × o * per l'AND, in quanto per alcuni versi questi operatori lavorano in modo analogo alla somma e alla moltiplicazione. La negazione NOT viene rappresentata spesso da una linea disegnata sopra l'argomento della negazione, cioè dell'espressione che deve essere negata. Oppure in informatica si utilizza il simbolo | o || per l'OR, & o && per l'AND, e ~ o ! per NOT (es. A OR B AND NOT C equivale a A|B & ~C oppure a A+B*!C). Se ci riferisce agli operatori con i simboli di somma e moltiplicazione e poi intende la negazione come se fosse un'"elevazione a potenza", è facile da ricordare l'ordine di applicazione degli operatori: prima si applicano le negazioni, poi le AND e poi le OR.
Nella progettazione di circuiti elettronici, vengono utilizzati anche gli operatori brevi NAND (AND negato), NOR (OR negato) e XNOR (XOR negato): questi operatori, come XOR, sono delle combinazioni dei tre operatori base e vengono usati solo per rendere la notazione più semplice.
Operatori:
- NOT - simboli alternativi: x, ~, ¬, ! (in C, C++, C# e JavaScript)
- AND - simboli alternativi: *, , &, && (in C, C++, C# e JavaScript), BUT (se usato insieme al NOT)
- OR - simboli alternativi: +, , |, || (in C, C++, C# e JavaScript)
- XOR - simboli alternativi: ⊕, , ∨, ^, EOR, orr
- NAND - simbolo alternativo: ↑
- NOR - simbolo alternativo: ↓
- XNOR - simbolo alternativo: ≡, EQU
Valori:
- vero - simboli alternativi: true, 1, ON, SÌ (YES), alto
- falso - simboli alternativi: false, 0, OFF, NO, basso
In elettronica digitale viene definito vero un bit 1, sia in Input sia in Output, che di solito assume il valore di 5 V, mentre viene definito falso un bit 0, sia in Input sia in Output, che assume il valore di 0 V.
Di seguito sono indicati gli operatori più comuni e le rispettive porte logiche:
NOT[modifica | modifica wikitesto]
L'operatore NOT restituisce il valore inverso a quello in entrata. Una concatenazione di NOT è semplificabile con un solo NOT in caso il numero di ripetizioni sia dispari o con nessuno nel caso il numero di ripetizioni sia pari. Inoltre la porta logica NOT possiede una sola variabile binaria.
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Spesso, al fine di semplificare espressioni complesse, si usano operatori brevi che uniscono l'operazione di NOT ad altre: questi operatori sono NOR (OR + NOT), NAND (AND + NOT), XNOR (XOR + NOT). La negazione, in questi casi, viene applicata dopo il risultato dell'operatore principale (OR, AND, XOR).
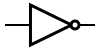
Il simbolo di una porta NOT è
Buffer[modifica | modifica wikitesto]
Buffer è la negazione del risultato dell'operazione NOT; restituisce il valore uguale a quello in entrata. Il Buffer non è un vero e proprio operatore, poiché in realtà non manipola l'informazione che riceve, bensì la lascia passare invariata; il Buffer dunque è semplificabile con un collegamento privo di operatori.
| A | Buffer A |
|---|---|
| 0 | 0 |
| 1 | 1 |
Il simbolo di una porta Buffer è:
composta da un NOT in serie a un altro NOT.
La ragione per cui si parla di questo "pseudo-operatore" è data da questioni di sincronia dei segnali: quando si tratta di circuiti e reti logiche in modo più approfondito si rende necessario considerare anche il tempo in cui il segnale arriva e l'elemento buffer viene interpretato in questi casi come un ritardo applicato a un certo segnale.
AND[modifica | modifica wikitesto]
L'operazione AND restituisce come valore 1 se tutti gli elementi hanno valore 1, mentre restituisce 0 in tutti gli altri casi come ad esempio quando una porta è alta mentre le altre sono basse e può essere messa in serie. Tale operazione è anche detta prodotto logico. Di seguito la tabella rappresenta l'operatore AND nel caso di due entrate, ma la definizione data ora è generalizzata a n ingressi:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Siccome questa operazione gode della proprietà associativa, è possibile realizzare un'operazione logica AND con un numero di proposizioni arbitrarie concatenando varie AND a due ingressi, per esempio:
Nei circuiti digitali, la porta logica AND è un meccanismo comune per avere un segnale di vero se un certo numero di altri segnali sono tutti veri.
Nella teoria degli insiemi corrisponde all'intersezione.
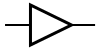
Il simbolo di una porta AND è:
OR[modifica | modifica wikitesto]
L'operazione logica OR restituisce 1 se almeno uno degli elementi è 1, mentre restituisce 0 in tutti gli altri casi. Tale operazione è anche detta somma logica. Di seguito la tabella rappresenta l'operatore OR nel caso di due entrate, ma la definizione data ora è generalizzata a n ingressi:
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Siccome questa operazione gode della proprietà associativa, è possibile realizzare un'operazione logica OR con più ingressi concatenando varie OR a due ingressi, per esempio:
Nei circuiti digitali, la porta logica OR è un meccanismo comune per avere un segnale alto se almeno un segnale è alto e un segnale basso se e solo se tutti i segnali sono bassi.
Nella teoria degli insiemi corrisponde all'unione.
Il simbolo di una porta OR a due ingressi è:
XOR[modifica | modifica wikitesto]
L'operatore XOR, detto anche EX-OR, OR esclusivo o somma modulo 2, restituisce 1 se e solo se il numero degli operandi uguali a 1 è dispari, mentre restituisce 0 in tutti gli altri casi. La tabella rappresenta il caso in cui gli operatori siano 2, poi in generale ci si riferisce a questo operatore come operatore di disparità.
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nella teoria degli insiemi corrisponde alla differenza simmetrica. Per passare nella forma canonica SP (somma di prodotti) basta applicare la regola:
A⊕B
dove ⊕ è il simbolo di XOR.
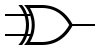
Il simbolo di una porta XOR è:
NAND[modifica | modifica wikitesto]
L'operatore NAND, la negazione del risultato dell'operazione AND, restituisce 0 se e solo se tutti gli elementi sono 1, mentre restituisce 1 in tutti gli altri casi.
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
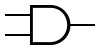
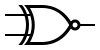
Il simbolo di una porta NAND è:
La porta NAND è composta da una porta NOT in serie ad una AND.
Utilizzando le leggi di De Morgan, è possibile convertire una porta OR in NAND. Vale, dunque, la seguente relazione:
NOR[modifica | modifica wikitesto]
L'operatore NOR, la negazione del risultato dell'operazione OR, restituisce 1 se e solo se tutti gli elementi sono 0, mentre restituisce 0 in tutti gli altri casi.
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Il simbolo di una porta NOR è:
composta da un NOT in serie a un OR.
Utilizzando le leggi di De Morgan, è possibile convertire una porta AND in NOR. Vale, dunque, la seguente relazione:
XNOR[modifica | modifica wikitesto]
L'operatore XNOR, detto anche EX-NOR o EQU, è la negazione del risultato dell'operazione XOR; nella sua versione a due elementi restituisce 1 se tutti gli elementi sono uguali a 1 oppure se tutti gli elementi sono uguali a 0. Questo operatore viene generalizzato a n ingressi come operatore di parità, cioè è un'operazione che restituisce il valore 1 se il numero di 1 in ingresso è pari.
| A | B | A XNOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Il simbolo di una porta XNOR è:
composta da un NOT in serie a un XOR.
Algebra dei circuiti[modifica | modifica wikitesto]
Come hanno mostrato già i primi studi pionieristici di J. Piesch[1], l'Algebra di Boole si presta bene allo studio degli insiemi, delle proposizioni e dei circuiti. Ci si vuole soffermare su come quest'algebra diventa uno strumento per l'analisi e la sintesi delle reti di commutazione (in elettrotecnica il termine viene usato per indicare un cambio d'ordine della chiusura di due o più contatti elettrici, in telecomunicazioni ha un'accezione diversa).
L'algebra booleana consente di descrivere in forma algebrica le funzioni dei circuiti componenti e delle reti, fornendo altresì i metodi per la realizzazione del progetto logico: è stabilita quindi una corrispondenza biunivoca fra espressioni algebriche e reti di commutazione. La corrispondenza è facilmente realizzabile avendo già parlato di Operatori booleani: si parte ad esempio da un'espressione algebrica per realizzare un circuito, basta sostituire a ogni operatore logico la corrispondente porta logica e applicare agli ingressi di queste opportunamente le variabili booleane in gioco; inoltre, avendo visto l'esistenza di porte logiche come ad esempio la XOR, che sono combinazioni degli operatori booleani elementari AND, OR e NOT, è possibile manipolare opportunamente un'espressione algebrica in modo da utilizzare il minor numero possibile di porte nella realizzazione del circuito. Viceversa un circuito può essere espresso da una funzione y=f(x1,x2,...xn) dove y è l'uscita, le x sono le entrate e la funzione f è una combinazione di porte logiche.
Nell'algebra dei circuiti si associa il valore 0 al livello logico basso e il valore 1 al livello logico alto. In una visione semplificata il valore 0 corrisponde nella pratica a una tensione di 0 V mentre il valore 1 corrisponde a 5 V, oppure 3,5 V o addirittura 1,5 V: il motivo per cui si preferisce associare il valore alto a 5 V piuttosto che a 1,5 V è che la tensione nella pratica non è stabile e perciò il valore 0 si può "confondere" con il valore 1 causando una perdita di informazione; d'altra parte però, una tensione di 1,5 V per indicare il valore alto significa minor dispendio di energia ed è un vantaggio molto significativo.
Volendo approfondire il discorso sui valori logici alto e basso e sulla loro realizzazione pratica, si può dire che, a seconda della tecnologia ci sono diversi range di valori possibili: per esempio, la tecnologia TTL associa il valore logico 0 a una tensione compresa tra 0 V e 0,8 V, tra 0 e 2 V c'è una banda vietata, cioè un insieme di valori che non devono essere assunti, e il valore logico 1 è associato al range di valori 1,5 V - 5 V. Come si è accennato, la tecnologia odierna spinge sull'abbassare la soglia dei 5 V cercando di stabilizzare sempre di più il potenziale.
Esempi[modifica | modifica wikitesto]
Questa algebra ha applicazioni nella logica, dove 0 è interpretato come "falso", 1 come "vero", è OR, è AND e è NOT. Le espressioni che coinvolgono le variabili e le operazioni booleane rappresentano forme dichiarative; due espressioni possono essere equivalenti utilizzando i suddetti assiomi se e soltanto se le forme dichiarative corrispondenti sono logicamente equivalenti. L'algebra booleana binaria, inoltre, è usata per il disegno di circuiti nell'ingegneria elettronica; qui 0 e 1 rappresentano le due condizioni differenti di un bit in un circuito digitale, in genere bassa e alta tensione. I circuiti sono descritti da espressioni che contengono delle variabili e due espressioni sono uguali per tutti i valori delle variabili se e soltanto se i circuiti corrispondenti hanno la stessa funzione di trasferimento. Ogni combinazione dei segnali in ingresso in uscita dal componente può essere rappresentata da un'adeguata espressione booleana
L'algebra booleana a due stati è inoltre importante nella teoria generale delle algebre booleane, perché un'equazione che coinvolge parecchie variabili è generalmente vera in ogni algebra booleana se e soltanto se è vera nell'algebra booleana a due stati. Ciò può, per esempio, essere usato per indicare che le seguenti leggi (teorema del consenso) sono generalmente valide in ogni algebra booleana:
- Il raggruppamento di un generico insieme S, forma un'algebra booleana con le due operazioni = unione e = intersezione. Il più piccolo elemento 0 è l'insieme vuoto e il più grande elemento 1 è l'insieme S stesso.
- L'insieme di tutti i sottoinsiemi di un insieme S che sono limitati è un'algebra booleana.
- Per ogni numero naturale n, l'insieme di tutti i divisori positivi di n forma un reticolo distributivo se scrive per a divide b. Questo reticolo è un'algebra booleana se e soltanto se per ogni n non vi sono divisori quadrati. Il più piccolo elemento, che in generale si indica con lo 0, in questa algebra booleana è il numero naturale 1; mentre l'elemento che usualmente indica con l'1 in questi insiemi è l'elemento "n".
- Altri esempi di algebre booleane sono dati dagli spazi topologici: se X è uno spazio topologico, allora l'insieme di tutti i sottoinsiemi di X che siano aperti o chiusi formano un'algebra booleana con le operazioni = unione e = intersezione.
- Se R è un anello arbitrario dove è definito un insieme idempotente tipo:
A = { a in R : a2 = a e ax = xa per ogni x in R }
L'insieme A diventa un'algebra booleana con le operazioni ab = a + b − ab e ab = ab.
Omomorfismi e isomorfismi[modifica | modifica wikitesto]
Un omomorfismo tra due algebre booleane A e B è una funzione f: AB tale che per ogni a, b in A:
- f( a b ) = f( a ) f( b )
- f( a b ) = f( a ) f( b )
- f(0) = 0
- f(1) = 1
Da queste proprietà segue anche f(a) = f(a) per ogni a in A. Ogni algebra booleana, con la definizione di omomorfismo, forma una categoria. Un isomorfismo da A su B è un omomorfismo da A su B che è biiettivo. L'inverso di un isomorfismo è ancora un isomorfismo, e le due algebre booleane A e B si dicono isomorfe. Dal punto di vista della teoria dell'algebra booleana, due algebre booleane isomorfe non sono distinguibili, ma differiscono soltanto nella notazione dei loro elementi.
Espressioni booleane[modifica | modifica wikitesto]
All'interno di ciascuna algebra di Boole, dato un insieme di variabili e le operazioni correlate, è possibile definire delle espressioni che vengono ad assumere un determinato valore ottenibile anche sotto forme diverse. Possono esistere cioè delle espressioni che, pur essendo differenti, si rivelino equivalenti. Oltre al fatto che le espressioni booleane assumono una particolare importanza per quanto riguarda il calcolo proposizionale, in cui le variabili sono proposizioni legate tramite congiunzioni, disgiunzioni, negazioni e altre operazioni più complesse, possono esistere moltissime altre espressioni, accomunate sempre dalle proprietà e dagli assiomi booleani, nelle quali si sostituisce spesso l'operazione + (comunemente detta somma) con ∨ e * (comunemente detta prodotto) con ∧ e in cui la complementazione è indicata col simbolo ' .
Per poter presentare nel modo più efficiente un'espressione booleana, la si riduce in somma di prodotti fondamentali o forma normale disgiuntiva. Un prodotto fondamentale è un prodotto in cui ciascuna variabile, o il suo complemento, appaia una sola volta e rigorosamente fuori da parentesi o complementazioni complesse.
Ad esempio, date le variabili x, y, z all'interno di un'algebra di Boole, sono prodotti fondamentali
- P(x,y,z) = xy
- P(x,y,z) = x'yz'
Mentre non sono prodotti fondamentali
- yyz
- yy'z
- (xy)'
È così possibile avere una somma di prodotti fondamentali, forma in cui ogni espressione può essere ridotta, ma che non è unica. Un esempio è: xy + xz + z'. Nel momento in cui ogni singola variabile, o il suo complemento, siano contenuti in tutti i prodotti fondamentali della forma normale disgiuntiva, si ha allora una somma di prodotti fondamentali completa o forma normale disgiuntiva completa. Tale scrittura è unica, pertanto se due espressioni sono equivalenti avranno la stessa forma normale disgiuntiva completa.
Se si desidera invece che un'espressione sia scritta nel modo più corto possibile, allora la si esprime in somma di implicanti prime o minimali (Minimizzazione di Quine-McQluskey). Un'implicante prima (o minimale) rispetto a un'espressione è un prodotto fondamentale che non altera l'espressione se sommato per intero a essa, cioè restituisce un risultato equivalente a quella iniziale; sommando un prodotto strettamente contenuto nell'implicante, tuttavia, non si ottiene un'equivalenza.
Per individuare tutte le implicanti prime, esistono varie tecniche, tra cui il metodo del consenso, che si basa sull'applicazione ciclica delle proprietà di assorbimento, idempotenza, involuttività e di De Morgan accompagnate a ogni passo dall'opportuna addizione di un consenso. Dati due prodotti fondamentali, se solo e solo se una variabile appare in uno di essi non negata e nell'altro negata si chiama consenso il risultato della moltiplicazione delle restanti variabili. Ad esempio:
- dati P = xyz, Q = x'z il consenso sarà C = yzz = yz
- dati P = xy' Q= xy il consenso sarà C = xx = x
- dati P = xyz e Q = x'yz' non esiste consenso, in quanto due diverse variabili appaiono una volta negate e una volta no.
La somma di implicanti prime è unica, pertanto due espressioni equivalenti avranno la stessa. Nel momento in cui, completando ogni singola implicante prima, l'apporto all'espressione di una o più di esse è inutile in quanto contenuta nelle altre, la si può eliminare ottenendo la più essenziale delle scritture, la forma minimale. Essa, pur essendo comoda, ha l'inconveniente di non essere unica, e dunque di non consentire l'individuazione di equivalenze tra più espressioni.
Rappresentazione delle algebre booleane[modifica | modifica wikitesto]
Si può dimostrare che ogni reticolo booleano finito è isomorfo al reticolo booleano di tutti i sottoinsiemi di un insieme finito. Di conseguenza, il numero di elementi di ogni reticolo booleano finito ha un sostegno che contiene un numero di elementi uguale a una potenza di 2.
Marshall Stone ha enunciato il celebre teorema di rappresentazione per le algebre booleane dimostrando che ogni algebra booleana "A" è isomorfa a tutte le algebre booleane aperte-chiuse in un certo spazio topologico compatto non connesso di Hausdorff.
Note[modifica | modifica wikitesto]
- ^ (DE) H. Piesch, H. Sequenz, Die Österreichischen Wegbereiter der Theorie der Elektrischen Schaltungen (I pionieri austriaci della teoria della commutazione elettrica), Elecktrotechnik & Maschinenbau, Vol. 75, pp. 241-245
Bibliografia[modifica | modifica wikitesto]
- Giuseppe Calabrese, Le basi dell'elettronica - L'algebra di Boole, Milano, Editoriale Delfino, 1973.
- Giuseppe Calabrese, L'algebra di Boole. La logica applicata agli automatismi, Milano, Editoriale Delfino, 1974.
- (EN) Steven Givant e Paul Halmos, Introduction to Boolean Algebras, Undergraduate Texts in Mathematics, Springer, 2009, ISBN 978-0-387-40293-2.
- (EN) George Boole, An Investigation of the Laws of Thought, Prometheus Books, 2003 [1854], ISBN 978-1-59102-089-9.
- (EN) Steven Givant e Paul Halmos, Introduction to Boolean Algebras, Undergraduate Texts in Mathematics, Springer, 2009, ISBN 978-0-387-40293-2.
- (EN) John A. Camara, Electrical and Electronics Reference Manual for the Electrical and Computer PE Exam, Professional Publications Inc., 2010, p. 41, ISBN 978-1-59126-166-7.
Voci correlate[modifica | modifica wikitesto]
- 06-XX, sezione primaria dello schema di classificazione MSC 2000
- Algebra di insiemi
- Connettivo logico
- Diagramma di Venn
- Forma canonica
- Funzione booleana
- Mappa di Karnaugh
- Operazione bit a bit
- Porta logica
- Sistema formale
- Sistema numerico binario
- Tabella della verità
- Teorema dell'assorbimento
- Teorema di Shannon
- Teoremi di De Morgan
- Teoria degli insiemi
- Algebra di Robbins
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «algebra di Boole»
Wikizionario contiene il lemma di dizionario «algebra di Boole» Wikiversità contiene risorse sull'algebra di Boole
Wikiversità contiene risorse sull'algebra di Boole Wikimedia Commons contiene immagini o altri file sull'algebra di Boole
Wikimedia Commons contiene immagini o altri file sull'algebra di Boole
Collegamenti esterni[modifica | modifica wikitesto]
- Silvio Bozzi, Algebra di Boole, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
- àlgebra di Boole, su sapere.it, De Agostini.
- Boole, algebra di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- Boole, algebra di, in Dizionario di Economia e Finanza, Istituto dell'Enciclopedia Italiana, 2012.
- (EN) Boolean algebra, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Javier Legris, The Algebra of Logic Tradition, su Stanford Encyclopedia of Philosophy.
- (EN) Opere riguardanti Algebra di Boole, su Open Library, Internet Archive.
- Introduzione all’algebra Booleana (PDF), su isgroup.unimo.it.
- Panoramica sull'Algebra Booleana (PDF), su wwwusers.di.uniroma1.it.
- Facoltà di Ingegneria Energetica - Univ. del Sannio - Elementi di Informatica: Algebra di Boole 2008/2009 (PDF), su ing.unisannio.it. URL consultato il 13 agosto 2012 (archiviato dall'url originale il 24 dicembre 2012).
- Corso di Laurea a distanza - Fondamenti di Informatica: Algebra di Boole, Operatori Logici, Teoremi Fondamentali (PDF), su corsiadistanza.polito.it.
- Descrizione dell'algebra booleana su Okpedia, su okpedia.it.
| Controllo di autorità | Thesaurus BNCF 17741 · LCCN (EN) sh85003429 · GND (DE) 4146280-4 · BNE (ES) XX4576349 (data) · BNF (FR) cb119793249 (data) · J9U (EN, HE) 987007293933005171 · NDL (EN, JA) 00560863 |
|---|