Addizione

1+1=2

L'addizione (denotata normalmente dal simbolo del più, "+") è una delle quattro operazioni fondamentali dell'aritmetica, insieme alla sottrazione, alla moltiplicazione e alla divisione. L'addizione di due numeri naturali può essere definita in termini insiemistici. Per sommare due numeri naturali a e b, si considerano due insiemi A e B che abbiano, rispettivamente, a e b come numero di elementi, e che siano disgiunti (cioè non abbiano elementi in comune). Allora il risultato dell'addizione di a e b è il numero di elementi dell'insieme unione di A e B (l'insieme A ∪ B).

Ad esempio, se in un sacchetto abbiamo tre mele e in un altro sacchetto abbiamo due mele, mettendo insieme il contenuto dei due sacchetti avremo cinque mele. Questa osservazione è equivalente all'espressione matematica "3 + 2 = 5", ovvero "3 più 2 è uguale a 5".

3 + 2 = 5 usando le mele.

L'addizione può essere definita anche su quantità più astratte, quali i numeri interi relativi, i numeri razionali, i numeri reali e i numeri complessi, e su altri oggetti matematici quali i vettori e le matrici.

L'addizione gode di alcune proprietà basilari. È commutativa, ovvero cambiando l'ordine degli addendi la somma non cambia. È associativa, ovvero quando si sommano più di due numeri, il risultato è lo stesso indipendentemente dall'ordine in cui vengono effettuate le addizioni. Lo zero è l'elemento neutro dell'addizione, ovvero sommare zero ad un numero lascia quel numero invariato.

Notazione

I numeri o termini coinvolti nell'addizione sono collettivamente detti addendi, e il risultato dell'addizione è la loro somma.

Se gli addendi sono scritti individualmente, l'addizione è rappresentata dal carattere "+", che si interpone tra un termine e l'altro. Tra la sequenza degli addendi e la loro somma si interpone il simbolo dell'uguaglianza, "=". Sono addizioni valide:

Il simbolo dell'addizione

$3+2=5$

$998+1+1=1000$

$1+1+2+3+5+8+13+21=54$

e la prima di queste si legge, indifferentemente,

• "tre più due è uguale a cinque",
• "tre più due uguale cinque",
• o anche, sottintendendo il segno di uguale, soprattutto nelle addizioni brevi, nella forma "tre più due cinque"; oppure usare il monosillabo "fa" "tre più due fa cinque".

Negli scritti precedenti al XVI secolo è possibile trovare un altro simbolo indicante l'addizione. Si tratta di una "P" in corsivo che rimpiazzava la parola "più".

Il precedente simbolo dell'addizione. Una P in corsivo.

Se i termini non sono scritti individualmente, ma la sequenza degli addendi si ricava facilmente dalla scrittura, la somma si può indicare con un'ellissi ("...") per indicare i termini mancanti: la somma dei numeri naturali da 1 a 100 si può dunque scrivere come 1 + 2 + … + 99 + 100 = 5050.

In alternativa, la somma può essere rappresentata con il simbolo di sommatoria, rappresentato dalla lettera greca Sigma maiuscola. In particolare, data una sequenza di numeri denotati con $x_{1},\,...,x_{m},\,...x_{n},\,...$, la somma degli n-m+1 compresi fra quello di posizione m e quello di posizione n può essere espressa con la scrittura

$\sum _{i=m}^{n}x_{i}=x_{m}+x_{m+1}+x_{m+2}+\dots +x_{n-1}+x_{n}.$

Il simbolo "+" è un'abbreviazione della parola latina et, che significa "e". Il suo uso in opere a stampa è attestato sin dal 1486.

Interpretazione intuitiva

Combinazione di insiemi

Una delle interpretazioni dell'addizione è quella della combinazione di insiemi:

• Quando due o più collezioni disgiunte vengono combinate in un'unica collezione, il numero di oggetti nella collezione risultante è la somma dei numeri di oggetti nelle collezioni originali.

Questa interpretazione, facile da visualizzare, è anche alla base della definizione formale di addizione tra numeri cardinali.

Estensione di lunghezze

Una rappresentazione grafica dell'addizione 2 + 4 = 6. Una traslazione di 2 unità seguita da 4 traslazioni di 1 unità è equivalente ad una traslazione di 6 unità.

Una seconda interpretazione dell'addizione è data dall'estensione di una lunghezza (intera) di partenza in termini di una lunghezza (intera) data:

• La lunghezza corrispondente alla somma di due lunghezze a e b è ottenuta aumentando la lunghezza a di una unità per b volte.

Questa interpretazione è alla base della definizione formale di addizione tra numeri ordinali.

Definizione formale

A partire dalla funzione successore, introdotta dagli assiomi di Peano per definire un modello per i numeri naturali, si può formulare ricorsivamente una definizione rigorosa di addizione tra naturali.

Sia pertanto $(\mathbb {N} ,0,S)$ un modello per i numeri naturali dove $S\colon \mathbb {N} \to \mathbb {N}$ è la funzione successore che soddisfa gli assiomi di Peano. L'addizione in $\mathbb {N}$ è quindi l'operazione binaria interna

$+\colon \mathbb {N} \times \mathbb {N} \longrightarrow \mathbb {N} ,$

tale che:

• per ogni $m\in \mathbb {N}$ vale $m+0=m;$
• per ogni $m,n\in \mathbb {N}$ si ha che $m+S(n)=S(m+n).$

Proprietà

Commutatività

La proprietà commutativa: aggiungere tre mele ad un gruppo di due equivale ad aggiungerne due ad un gruppo di tre

L'addizione è un'operazione commutativa, ovvero cambiando l'ordine degli addendi il risultato non cambia:

$a+b=b+a.$

Ad esempio: $2+3=5=3+2.$

Associatività

Esempio visivo dell'associatività: 2+(1+3) = (2+1)+3

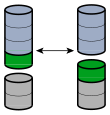
L'addizione è un'operazione associativa, ovvero quando si sommano tre o più addendi, l'ordine delle operazioni non influisce sul risultato:

$(a+b)+c=a+(b+c).$

Ad esempio: $(3+5)+2=8+2=10=3+7=3+(5+2).$

Esistenza dell'elemento neutro

Aggiungere zero ad un numero qualunque lascia quel numero invariato; in altre parole, lo zero è l'elemento neutro dell'addizione. In formule,

$a+0=0+a=a.$

Questa proprietà fu identificata nel Brahmasphuta Siddhānta di Brahmagupta nel 628 d.C., anche se formulata a parole ed in termini di tre leggi separate a seconda che a fosse negativo, positivo o zero. Altri matematici indiani elaborarono successivamente l'idea; intorno all'830 d.C., Mahāvīra scriveva che "lo zero diventa ciò che viene sommato ad esso", il che equivale alla proprietà 0 + a = a. Nel XII secolo, Bhāskara II scriveva: "Con l'addizione dello zero, o con la sua sottrazione, la quantità, positiva o negativa, rimane la stessa", il che equivale alla proprietà a + 0 = a.

Calcolo dell'addizione

Il riporto

Per eseguire velocemente un'addizione fra numeri naturali, si allineano in colonna gli addendi, partendo dalla cifra delle unità a destra. Dopodiché si sommano le cifre di ciascuna colonna, da destra verso sinistra, e nell'eventualità che il risultato della somma su una colonna sia maggiore o pari a dieci, si "riportano" le decine in eccesso come ulteriore addendo sulla colonna immediatamente a sinistra a quella appena calcolata.

Ad esempio, nell'addizione 27 + 59,

  ¹
  27
+ 59
————
  86

7 + 9 = 16, e la cifra 1 è il riporto.

Algoritmo dell'addizione

Il metodo discusso sopra può essere applicato per sommare due qualunque numeri naturali ad n cifre A=a_n-1...a₁a₀ e B=b_n-1...b₁b₀ (nel caso il numero di cifre di A e B sia diverso, è sufficiente aggiungere il numero appropriato di zeri in testa al numero con meno cifre). In pseudocodice, l'algoritmo è il seguente:

 function somma(an-1...a1a0, bn-1...b1b0)
     for i ← 0 to n-1 do
        r ← 0
        s ← ai + bi + r
        r ← s div 10     (calcolo del riporto)
        ci ← s mod 10
        return rcn-1...c1c0

Addizione di frazioni decimali

Seguendo un metodo simile a quello descritto sopra si possono sommare anche due frazioni decimali. Si allineano i due numeri decimali in modo tale che la virgola sia nella stessa posizione. Se necessario, si aggiungono degli zeri in coda al numero più corto perché abbia lo stesso numero di cifre di quello più lungo. Infine, si segue il procedimento visto sopra, con l'unica accortezza di aggiungere la virgola al risultato nella stessa posizione in cui compare nei due addendi. Ad esempio, 45,1 + 4,34 si svolge nel seguente modo:

   4 5, 1 0 +
   0 4, 3 4 =
——————————————
   4 9, 4 4

Questa estensione del metodo fu divulgata da Simone Stevino.

Generalizzazioni

Nella teoria dell'algebra astratta si può chiamare "addizione" una qualunque operazione associativa e commutativa definita su un insieme, che sia dotata di un elemento neutro. Una struttura algebrica che includa una simile operazione è detta monoide commutativo.

Storia

Già gli antichi Egizi avevano un semplice metodo per sommare numeri naturali. Nella notazione geroglifica, i numeri venivano indicati ripetendo una quantità appropriata di simboli rappresentanti le unità, le decine, le centinaia, eccetera. Per ottenere la somma di due numeri, quindi, era sufficiente combinare le unità, poi le decine, poi le centinaia, e così via, con l'accortezza di rimpiazzare eventuali gruppi di dieci simboli identici con un simbolo del tipo successivo. Ad esempio, per sommare 783 e 275, si combina

con

ottenendo

che semplificato diventa

(cioè 1058).

Il metodo di addizione posizionale moderno era sicuramente già noto in India intorno all'anno 600 d.C., ma è assai plausibile che lo stesso genere di algoritmo fosse già utilizzato dai Babilonesi in Mesopotamia nel 1700 a.C., anche se in un sistema sessagesimale anziché decimale.

In Europa, l'algoritmo di addizione moderno fu introdotto nel XII secolo attraverso la traduzione degli scritti del matematico persiano al-Khwarizmi.

Bibliografia

• Richard Brent e Paul Zimmermann, Modern Computer Arithmetic, Cambridge University Press, 2011, ISBN 978-0-521-19469-3.
• Florian Cajori, A History of Mathematical Notations, Dover, 2003, ISBN 978-0-486-67766-8.
• Victor J. Katz, A History of Mathematics, 3ª ed., Pearson Education, 2009, ISBN 0-321-38700-7.
• Saunders Mac Lane e Garrett Birkhoff, Algebra, 3ª ed., American Mathematical Society, 1991, ISBN 0-8218-1646-2.
• Patrick Suppes, Abstract Set Theory, Dover, 1973, ISBN 0-486-61630-4.

Voci correlate

• Aritmetica
• Sottrazione
• Moltiplicazione
• Divisione
• Più

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «addizione»
• Wikimedia Commons contiene immagini o altri file sull'addizione

Collegamenti esterni

• Addizióne, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• addizione, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) addition, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Addizione, su MathWorld, Wolfram Research.
• L'OPERAZIONE DI ADDIZIONE, su Mauitaui e la matematica, mauitaui.org.
• Addizione in colonna, su Il genio della matematica.