Fisica classica

Nella storia della fisica con il nome di fisica classica si raggruppano tutti gli ambiti e i modelli della fisica che non considerano i fenomeni descritti nel macrocosmo dalla relatività generale e nel microcosmo dalla meccanica quantistica, teorie che definiscono invece la cosiddetta fisica moderna.
Per tale motivo è possibile classificare come fisica classica tutte le teorie formulate prima del XX secolo, all'iniziare del quale apparvero i primi lavori di Max Planck basati sull'ipotesi dei quanti. Alcune teorie successive, come la relatività ristretta[1], possono essere considerate classiche o moderne. Sono quindi comprese nella fisica classica le teorie sulla meccanica, inclusa l'acustica, sulla termodinamica, sull'elettromagnetismo, inclusa l'ottica, e la gravità newtoniana.
Nel XVII secolo fu sviluppato il metodo scientifico e si aprì una fase di indagine approfondita della natura condotta da celebri scienziati come Galileo Galilei, Isaac Newton e Gottfried Wilhelm von Leibniz. Gli studi si concentrarono sul moto dei corpi e le sue cause, con particolare riguardo verso la meccanica celeste, segnata dal confronto fra la teoria geocentrica e quella eliocentrica. L'attenzione della fisica nei due secoli successivi si estese all'elettrostatica e al magnetismo, alla termodinamica e infine all'elettrodinamica.
L'elettrodinamica classica rappresentò la prima unificazione di teorie che descrivono fenomeni differenti, come l'elettricità, il magnetismo e la luce, in un'unica sintesi matematica formulata da James Clerk Maxwell. Fu tuttavia proprio grazie allo studio delle equazioni di Maxwell che la fisica classica entrò in crisi. Alcuni fenomeni fisici che occorrono a scala microscopica e macroscopica come lo studio della forma dello spettro di corpo nero, il fallimento della teoria dell'etere luminifero e la scoperta di fenomeni come l'effetto fotoelettrico, il moto browniano, il modello dell'atomo di idrogeno, la diffrazione di Bragg, la non invarianza in forma delle equazioni di Maxwell rispetto alle trasformazioni di Galileo, la precessione del perielio dell'orbita di Mercurio ecc., generarono una serie di contraddizioni che in breve tempo misero in crisi il complesso apparato della fisica classica, aprendo la strada alla relatività speciale e alla meccanica quantistica e a tutta la fisica moderna del XX secolo.
Il progressivo sviluppo della matematica fu stimolato dalla fisica e rese possibile la nascita di nuove teorie che necessitavano di nuovi strumenti, come il calcolo differenziale, per poter essere formalizzate. Infatti la storia della matematica è intrecciata con quella della fisica classica, ed è proprio con lo sviluppo di quest'ultima che la scienza iniziò a servirsi di formule matematiche per rappresentare e sintetizzare le teorie sul comportamento della natura.
Storia[modifica | modifica wikitesto]

La storia della fisica classica coincide con la storia della fisica fino all'inizio del XX secolo, e si intreccia con la storia di tutte le altre scienze. La nascita della fisica classica non è databile, in quanto i primi elementi di questa scienza compaiono già nell'antichità, ancora prima della nascita del pensiero filosofico greco.[2] Infatti, nell'ambito delle osservazioni astronomiche, alcune popolazioni presenti nella mezzaluna fertile e nell'Europa preistorica avevano condotto le prime osservazioni sull'orbita dei pianeti del sistema solare, del sole e della luna. Nell'antica Cina e nell'antica Grecia furono sviluppati anche strumenti in grado di calcolare gli eventi astronomici significativi del futuro, come le eclissi solari.[3] L'insieme di queste conoscenze può essere a ragione considerato una versione primordiale di alcune delle conoscenze della meccanica celeste.
In epoca successiva, sempre nella Grecia antica e nel mondo ellenistico e romano (scienza greco-romana), si svilupparono i primi rudimenti dell'idrostatica e dell'idrodinamica, grazie agli studi di Archimede,[2] con le loro applicazioni idrauliche; si ebbe un interesse per la termologia, con la costruzione delle prime macchine termodinamiche[4]; iniziarono i primi studi di ottica geometrica, meccanica e le prime speculazioni sull'esistenza dell'atomo. Nell'ambito della meccanica celeste furono poi sviluppati il sistema tolemaico e il sistema aristotelico che, sfruttando la geometria euclidea, descrivevano le orbite del moto dei pianeti. La scienza classica era di carattere speculativo e intrecciata alle teorie filosofiche dell'epoca, come l'atomismo.[5] La conoscenza e la descrizione della natura in ambito classico era quindi puramente qualitativa. L'universo era diviso nel mondo sopralunare, dove i moti sono circolari e senza fine, e nel mondo sublunare, dove i moti necessariamente hanno una fine e hanno una causa violenta che comporta l'allontanamento e il successivo ritorno al luogo naturale dei quattro elementi fondamentali, terra, acqua, aria e fuoco.[5]

Nel periodo medioevale fu grande il contributo scientifico che seppero dare i matematici, gli astronomi e gli ingegneri del califfato, grazie al periodo di relativo benessere e all'apertura delle rotte commerciali con le popolazioni dell'estremo oriente.[5] Si ebbe l'adozione del sistema posizionale per la rappresentazione dei numeri e la sostituzione del complesso sistema numerico romano con quello basato sulle cifre arabe avvenne anche in Europa. Nel frattempo venivano fondate le prime università e nel continente si affermava il principio dell'auctoritas, per cui le affermazioni fatte dai filosofi greci, come da Aristotele in campo fisico, venivano assunte come vere solo basandosi sul prestigio dell'autore[5][6][7].
Fu solo dopo la nascita del metodo scientifico, con l'importante contributo di Galileo Galilei, e con la comprensione che la scienza debba confrontarsi con l'esperimento che iniziò lo sviluppo della scienza per come la conosciamo oggi, e la progressiva ramificazione delle conoscenze in settori diversi, mano a mano che la mole di dati e fenomeni studiati aumentava.[5] Dopo i lavori di Galilei in ambito meccanico, astronomico e ottico, la deduzione delle tre leggi di Keplero, lo sviluppo della meccanica e delle sue applicazioni, l'introduzione del formalismo matematico come linguaggio di lavoro comune per i fisici, e soprattutto grazie all'opera di Isaac Newton, si realizzò una sistematizzazione del sapere scientifico nei Philosophiae Naturalis Principia Mathematica. Sempre allo stesso autore dobbiamo, oltre ai principi della dinamica, la scoperta, assieme a Leibniz, dell'applicazione alla fisica del calcolo infinitesimale e del calcolo integrale. Questi sviluppi portarono alla nascita della fisica matematica.[5]

La legge della gravitazione universale dedotta dallo scienziato inglese ha rappresentato uno dei capisaldi della fisica classica: qualsiasi fenomeno astronomico riscontrato fino al XIX secolo poteva essere spiegato da questa teoria. A Newton si deve anche la riduzione della teoria dell'ottica (ambito in cui nel frattempo si era scoperta la diffrazione) all'azione della gravità su ipotetiche particelle - i fotoni - di cui si pensava fosse composta la luce, e la creazione della cosiddetta teoria corpuscolare della luce, in contrapposizione alla teoria ondulatoria proposta da Christiaan Huygens.
Successivamente si sviluppò anche la teoria della termologia, e in particolare la termodinamica, che ricevette grande impulso dalle esigenze della rivoluzione industriale. L'esperimento cruciale per questa disciplina è stata la dimostrazione realizzata nel 1798 da Benjamin Thompson che il lavoro meccanico può essere convertito in calore, che all'epoca era considerato una sostanza detta calorico. Fu poi Joule a dimostrare l'equivalenza fra lavoro e calore, mentre Sadi Carnot sviluppò le teorie sulle macchine termodinamiche. L'intero apparato della teoria fu infine quindi ricondotto a concetti meccanici grazie allo sviluppo della teoria cinetica dei gas e alla prova della corrispondenza fra termodinamica e meccanica statistica.
Nel XIX secolo, alcune irregolarità nel moto di Urano furono spiegate prevedendo l'esistenza di un altro pianeta di grosse dimensioni, Nettuno.[8] Anche la precessione del perielio dell'orbita di Mercurio si discostava da quanto predetto dalla gravitazione, ma a questo problema non fu trovata soluzione.
Fino ad allora tutte le scienze erano state ricondotte ad avere sostanzialmente una base meccanica, tanto che questa era ormai considerata la base di qualsiasi tipo di esperienza fisica, e aveva dato origine a una corrente di pensiero chiamata meccanicismo, che ne postulava l'applicabilità in ogni ambito. Scrive Einstein a questo proposito:[9]

«Non dobbiamo quindi stupirci [visti i risultati di questa scienza] se tutti, o quasi tutti gli scienziati del secolo scorso videro nella meccanica classica la base sicura e definitiva di tutta la fisica, anzi addirittura di tutte le scienze naturali [...]»
Tuttavia, sempre a partire dal XIX secolo iniziarono gli studi sperimentali sui fenomeni elettrici e magnetici, che proseguirono di pari passo con la creazione di accumulatori come le bottiglie di Leida, risalenti al 1746, e generatori come la pila di Volta, sviluppata intorno al 1800. Con l'esperimento di Ørsted (1820) si scoprì che correnti elettriche generano campi magnetici, e successivamente il teorema di equivalenza di Ampère stabilì che un dipolo magnetico è equivalente a una spira percorsa da corrente elettrica, e ciò si può interpretare asserendo che il campo magnetico viene generato da correnti elettriche. Sin dall'esperimento di Ørsted si sapeva che elettricità e magnetismo erano correlati, ma non se conoscevano i meccanismi; nel 1873 James Clerk Maxwell sintetizzò le leggi dell'elettrodinamica nelle equazioni di Maxwell, che portano il suo nome, creando una teoria unitaria dell'elettricità e del magnetismo.[5] L'aspetto cruciale delle nuove equazioni fu la scoperta teorica dell'esistenza della radiazione elettromagnetica, scoperta confermata sperimentalmente da Heinrich Rudolf Hertz nel 1887.[5]
La comunità fisica cercò di spiegare anche l'elettromagnetismo nell'insieme dei principi della meccanica classica.[5] Fu sviluppata appositamente una teoria che faceva ricorso a una sostanza inventata ad hoc, chiamata etere, per tentare di descrivere la propagazione della luce come fenomeno meccanico. Sempre Einstein scrive:[10]
«Per poter ancora considerare la meccanica come il fondamento della fisica, bisognava interpretare meccanicamente anche le equazioni di Maxwell. Si tentò di farlo con molto impegno, ma senza risultato, mentre i risultati delle equazioni si dimostravano sempre più fecondi. [...] la meccanica come base della fisica stava per essere abbandonata, quasi inavvertitamente, perché la speranza di poterla adattare ai fatti si era alla fine dimostrata vana.»

Fu proprio la teoria dell'elettromagnetismo a determinare la fine del meccanicismo e della fisica classica. Per tentare di rendere compatibili le equazioni di Maxwell con le leggi della meccanica furono introdotte le trasformazioni di Lorentz. Ma in breve tempo ci si accorse che la meccanica andava modificata nelle sue basi più intime e di principio, ovvero nei concetti di spazio e tempo. Così facendo Albert Einstein fece nascere la relatività ristretta, che è l'ultima teoria che alcuni autori considerano classica.
Fra i problemi irrisolvibili dalla fisica classica, oltre alla precessione di Mercurio, vi erano poi la necessità di trovare l'origine dell'effetto fotoelettrico, ovvero la capacità della luce di indurre una corrente in un conduttore, o la forma dello spettro di corpo nero, ovvero la forma che assume l'intensità della radiazione emessa da un corpo nero in funzione dell'energia. Fu solo grazie rispettivamente alla teoria della relatività generale e alla nascita della meccanica quantistica, le cui basi erano già state poste nel 1900,[11] che questi fenomeni trovarono una spiegazione in una teoria fisica generale e coerente, che superasse le prime teorie semiclassiche. Iniziò così quella che viene definita la fisica moderna.[5]
Principi[modifica | modifica wikitesto]
I concetti di spazio e tempo assoluti e di determinismo furono oggetto di un lungo dibattito, fino a quando evidenze sperimentali determinarono il superamento della fisica classica come teoria capace di spiegare qualsiasi fenomeno naturale. Entrambi i concetti rivestirono un ruolo cardine prima nel guidare lo sviluppo e in seguito nel determinare la caduta delle teorie che vi si basavano.
Il secondo è un principio che si sviluppò man mano che progrediva la conoscenza della meccanica e che postulava il rigoroso determinismo del nostro universo. Secondo questa concezione, se l'universo fosse stato regolato da leggi meccaniche, poiché ognuna di queste è invariante rispetto all'inversione del tempo, allora avendo il controllo completo di tutte le variabili meccaniche di tutte le particelle dell'universo si sarebbe potuto predire la sua evoluzione futura senza alcun limite temporale.
Un ulteriore oggetto di grande dibattito nella fisica classica riguardò l'atomismo e la disputa sulla natura corpuscolare o ondulatoria della luce.[12]
Spazio e tempo assoluti[modifica | modifica wikitesto]

Il primo di questi principi vede lo spazio e il tempo come entità assolute, perpetue, la cui esistenza è il presupposto ai principi della dinamica di Newton.[13] Il tempo fu considerato inizialmente un ente assoluto, cioè percepito alla stessa maniera da tutti gli osservatori dell'universo conosciuto. Nella fisica moderna i due concetti sono venuti meno con la formulazione nella relatività speciale nel 1905.
L'esistenza di un tempo assoluto permetteva di definire con precisione quali fossero le relazioni causali nell'evoluzione fisica dell'universo: ciò che accadeva prima, in qualsiasi punto dell'universo, avrebbe potuto influenzare ciò che accadeva dopo, in qualsiasi altro punto dell'universo. La meccanica newtoniana prevedeva infatti che le interazioni a distanza (come la forza gravitazionale) si propagassero istantaneamente con una velocità infinita. L'idea di un tempo assoluto, percepibile allo stesso modo da tutti gli osservatori e nettamente separato dalla nozione di spazio, è accettata fino alla formulazione della relatività ristretta, nel 1905.
Il sistema tolemaico prevedeva un sistema di riferimento spaziale assoluto, che permettesse in particolare di definire la differenza fra oggetti fermi e oggetti in moto. La Terra era ferma al centro dell'universo e i corpi celesti si muovevano intorno ad essa, ogni oggetto aveva quindi una sua velocità ben definita. A partire dal Dialogo sopra i due massimi sistemi del mondo, intorno al 1630, Galileo si rese conto però che non vi può essere nessuna differenza fra le leggi della fisica (cioè in particolare della meccanica) descritte da un osservatore in moto rettilineo uniforme rispetto ad uno fermo:
«Rinserratevi con qualche amico nella maggiore stanza che sia sotto coverta di alcun gran navilio, e quivi fate d'aver mosche, farfalle e simili animaletti volanti: siavi anco un gran vaso d'acqua, e dentrovi de' pescetti; sospendasi anco in alto qualche secchiello, che a goccia a goccia vada versando dell'acqua in un altro vaso di angusta bocca che sia posto a basso; e stando ferma la nave, osservate diligentemente come quelli animaletti volanti con pari velocità vanno verso tutte le parti della stanza. [..] Osservate che avrete diligentemente tutte queste cose, benché niun dubbio ci sia mentre il vascello sta fermo non debbano succedere così: fate muovere la nave con quanta si voglia velocità; ché (pur di moto uniforme e non fluttuante in qua e in là) voi non riconoscerete una minima mutazione in tutti li nominati effetti; né da alcuno di quelli potrete comprendere se la nave cammina, o pure sta ferma.»
Nel suo celebre esperimento mentale della nave, Galileo nota come sia impossibile per un osservatore chiuso all'interno di una stanza di una nave costruire un esperimento per capire se la nave sia ferma al porto oppure in viaggio, a patto che il suo moto sia rettilineo e uniforme. Secondo la relatività galileiana, punto di base della meccanica newtoniana, non esiste nessun modo per distinguere un oggetto fermo da un oggetto che si muove con un moto rettilineo uniforme. La velocità assoluta di un oggetto non può essere quindi misurabile.
Le leggi della meccanica classica hanno la stessa forma nei sistema di riferimento inerziali,[15] in uno qualsiasi di questi sistemi in particolare i corpi liberi si muovono di moto rettilineo uniforme, le forze sono la causa della variazione dello stato moto in accordo con il secondo principio della dinamica e soddisfano il principio di azione e reazione.
La relatività galileiana entrò però in contrasto nel XIX secolo con le equazioni di Maxwell. Dalle equazioni emerse che la luce si muove ad una velocità fissata . La velocità della luce è quindi assoluta, contrariamente a quanto prescritto da Galileo. Alla fine dell'Ottocento vi furono vari tentativi per adattare il principio galileiano alla nuova teoria: si cercò di dimostrare l'esistenza di un sistema di riferimento inerziale privilegiato, l'unico in cui potessero valere (oltre a quelle di Newton) anche le equazioni di Maxwell, refrattarie al principio di relatività galileiano.
Fu prima Mach a criticare questo approccio. Secondo lui, l'inerzia di un sistema è il risultato delle interazioni di questo con tutte le masse dell'universo. Albert Einstein, a questo proposito, ebbe modo di notare:
«Nonostante il rigoglio delle ricerche particolari, in materia di princípi predominava una rigidezza dogmatica: in origine (se origine vi fu) Dio creò le leggi del moto di Newton insieme con le masse e le forze necessarie.[16]»
e ancora
«È necessario quindi, per giustificare la necessità della propria scelta specifica [di un sistema di riferimento], cercare qualcosa che sia al di fuori di ciò che è oggetto della teoria stessa (masse, distanze). Per questa ragione Newton introdusse in modo del tutto esplicito, come partecipante attivo onnipresente in tutti gli eventi meccanici, un elemento primario e determinante, lo "spazio assoluto" [...][17]»
Einstein risolse la contraddizione fra relatività galileiana e equazioni di Maxwell sostituendo la prima con quella che è adesso nota come relatività ristretta. Questo nuovo principio di relatività distrugge definitivamente il carattere assoluto di tempo e spazio. Il tempo percepito non è più assoluto. In particolare, due eventi in luoghi molto distanti possono risultare in ordine temporale invertito a seconda del sistema in cui sta l'osservatore. Spazio e tempo sono intrinsecamente legati e formano un quadridimensionale spaziotempo, la cui struttura matematica fu formalizzata successivamente con la nozione di spaziotempo di Minkowski.
Determinismo[modifica | modifica wikitesto]
Le leggi fisiche classiche determinano esattamente le traiettorie dei corpi, ad esempio consentono di prevedere completamente il moto dei pianeti e l'evoluzione sia futura che passata del sistema solare. Nel corso del XIX secolo questi successi spinsero a ipotizzare che la fisica, tramite le leggi matematiche, sarebbe stata in grado di conoscere tutta la storia passata e anche di predire l'esatta evoluzione futura dell'intero universo, posto che fosse stato possibile conoscere esattamente il valore delle velocità e delle posizioni di tutte le particelle in esso contenute in un dato momento.[18] Come scrisse Pierre Simon Laplace:[19]
«Nous devons envisager l'état présent de l'univers comme l'effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux. L'esprit humain offre, dans la perfection qu'il a su donner à l'astronomie, une faible esquisse de cette intelligence. Ses découvertes en mécanique et en géométrie, jointes à celles de la pesanteur universelle, l'ont mis à portée de comprendre dans les mêmes expressions analytiques les états passés et futurs du système du monde. En appliquant la même méthode à quelques autres objets de ses connaissances, il est parvenu à ramener à des lois générales les phénomènes observés, et à prévoir ceux que les circonstances données doivent faire éclore.»
«Dobbiamo considerare lo stato presente dell'universo come l'effetto del suo stato anteriore e come la causa del suo stato futuro. Un'intelligenza che, per un dato istante, conoscesse tutte le forze da cui è animata la natura e la situazione rispettiva degli esseri che la compongono, se per di più fosse abbastanza profonda per sottomettere questi dati all'analisi, abbraccerebbe nella stessa formula i movimenti dei più grandi corpi dell'universo e dell'atomo più leggero: nulla sarebbe incerto per essa e l'avvenire, come il passato, sarebbe presente ai suoi occhi. Lo spirito umano offre, nella perfezione che ha saputo dare all'astronomia, un pallido esempio di quest'Intelligenza. Le sue scoperte in meccanica e in geometria, unite a quella della gravitazione universale, l'hanno messo in grado di abbracciare nelle stesse espressioni analitiche gli stati passati e quelli futuri del sistema del mondo. Applicando lo stesso metodo ad altri oggetti delle sue conoscenze, è riuscito a ricondurre a leggi generali i fenomeni osservati, e a prevedere quelli che devono scaturire da circostanze date»

La completa determinazione dell'evoluzione dell'universo anche in ambito classico è possibile solo in linea di principio, tuttavia anche solo l'eventualità che la storia dell'universo sia completamente predeterminata fu sufficiente ad aprire un grande dibattito filosofico che spaziò fino a toccare temi come il libero arbitrio dell'uomo.[20] Infatti, seguendo l'argomentazione dello stesso Laplace, nessuno sarebbe mai stato in grado di avere una capacità di calcolo così vasta da poter permettere l'analisi dei successivi stati dell'universo ed inoltre nessuno avrebbe mai posseduto una conoscenza dello stato dell'universo in un dato istante abbastanza precisa da poter ottenere previsioni future accurate.

Per l'aspetto computazionale, il calcolo del moto dei corpi nella fisica classica è spesso possibile solo ricorrendo ad approssimazioni. Gli sforzi di alcuni fra i migliori fisici e matematici del XIX secolo furono rivolti a cercare di trovare soluzioni esatte a problemi, come quello famoso dei tre corpi, che non erano stati risolti analiticamente.[21] Non fu cioè possibile scrivere le traiettorie esatte nemmeno per un sistema di soli tre corpi che interagiscono gravitazionalmente, come ad esempio la Terra, la Luna e il Sole. Questo fallimento accadde perché il sistema a tre corpi, seppur descritto da leggi fisiche classiche, è solo uno degli esempi più antichi e maggiormente noti di sistema non integrabile, anzi, solamente di pochissimi sistemi fisici è possibile conoscerne l'andamento futuro esattamente.[22] In questi casi è possibile ottenere solo una soluzione approssimata, numerosi metodi di soluzione numerica per equazioni differenziali ordinarie sono stati infatti sviluppati e implementati nel XX secolo grazie all'ausilio dei moderni computer.[23]
Per l'aspetto dell'importanza della conoscenza precisa delle condizioni iniziali delle particelle, è noto che i sistemi non integrabili hanno la particolarità di dimostrare un'elevata sensibilità alle condizioni iniziali, che è una delle caratteristiche costitutive dei sistemi caotici.[24] Le previsioni meteorologiche sono ad esempio affidabili solamente con un orizzonte temporale di pochi giorni, dopodiché le incertezze nella conoscenza della temperatura, della pressione e dello stato attuale dell'atmosfera produrranno grosse variazioni rispetto alle previsioni. Questo fenomeno è noto come effetto farfalla.[24]

Lo sviluppo della meccanica quantistica agli inizi del XX secolo cambiò radicalmente i termini della disputa in merito al determinismo. Secondo l'interpretazione di Copenaghen è impossibile prevedere l'evoluzione di un sistema non tanto per l'ignoranza dello sperimentatore sulle condizioni iniziali del sistema, ma a causa di una caratteristica della teoria. Ne risulta che non è più possibile associare ad una particella una posizione ed una velocità definite con una precisione arbitraria[25]. La meccanica quantistica, infatti, descrive ogni sistema fisico tramite un vettore di stato. Da questa descrizione si deduce che il risultato dell'interazione deve tenere conto anche dei fenomeni di interferenza tra gli stati: il risultato determinato dalla teoria è, nella maggioranza dei casi,[26] un insieme composto da più stati possibili ai quali è associata una probabilità. Questo insieme tuttavia non è interpretabile con l'asserzione che il sistema si trova in uno stato o nell'altro con una certa probabilità, ma si deve invece interpretare considerando che il sistema è sia in uno stato sia nell'altro, ovvero in una sovrapposizione di stati; ciascuno dei quali è pesato con una propria probabilità. Numerosi esperimenti hanno dimostrato la validità di quest'interpretazione: ad esempio l'esperimento di Stern e Gerlach (realizzato nel 1922) e l'esperimento della doppia fenditura (realizzato nel 1961).[27]
A proposito del crollo del determinismo si ricorda una triplice citazione, organizzata in forma dialogica:
«Dio non gioca a dadi con l'universo»
«Piantala di dire a Dio che cosa fare con i suoi dadi.»
«Non solo Dio gioca a dadi, ma li getta laddove non possiamo vederli.»
Si vede dalle prime due citazioni come all'epoca della nascita della meccanica quantistica, questa caratteristica della teoria fosse controversa e che solo successivamente si pervenne ad accettarla come una caratteristica naturale[28]
L'atomismo e la natura della luce[modifica | modifica wikitesto]

L'atomismo e l'idea che la materia sia composta da unità elementari ed indivisibili furono introdotti fin dai primi passi dello studio della natura nell'ambito della filosofia della Grecia classica, per muoversi nell'ambito scientifico propriamente detto a partire dal XVII secolo.[29] Alcune delle prime evidenze sperimentali portate come argomento a favore della natura atomica, granulare e non continua della materia, furono l'osservazione dell'evaporazione dell'acqua e il passaggio di una soluzione attraverso serie di filtri.[12]
L'atomismo fu ripreso ed esteso nei Principia da Isaac Newton, che presentò una teoria atomistica anche per l'ottica, e quindi per la luce, in termini puramente meccanici come interazioni fra corpuscoli e particelle.[12] I primi esperimenti sulle reazioni chimiche furono sviluppati in una teoria atomica da John Dalton. Ulteriori conferme sulla natura corpuscolare della materia arrivarono dallo sviluppo della teoria cinetica dei gas nel XIX secolo. La natura corpuscolare della luce fu tuttavia oggetto di dibattito e messa in difficoltà dagli esperimenti di Thomas Young, che supportavano piuttosto l'ipotesi di Christiaan Huygens sulla natura ondulatoria della luce, come vibrazione e onda dell'etere. Gli esperimenti di Young mostravano l'interferenza della luce, fenomeno tipico delle onde ma inspiegabile con l'ipotesi che la luce sia composta da atomi.[30]
Nonostante i successi in ambito chimico e termodinamico dell'atomismo, ancora alla fine del 1800 e all'inizio del 1900 Ernst Mach criticò la realtà fisica degli atomi intesa al di fuori dell'ipotesi speculativa.[12] Ulteriori prove a favore dell'atomismo arrivarono dallo sviluppo della teoria statistica del moto browniano da parte di Albert Einstein nel 1905.[31] Sempre all'inizio del 1900, lo sviluppo della meccanica quantistica da una parte permise lo sviluppo di una teoria coerente in grado di spiegare il comportamento degli atomi, delle molecole e dei legami chimici; dall'altra pose fine alla disputa sulla natura della luce. Nella meccanica quantistica la luce e anche le particelle elementari della materia, come gli elettroni, sono descritti sia come un'onda che come una particella, in base al principio di complementarità.
Settori di studio[modifica | modifica wikitesto]
I vari settori di studio in cui suddividiamo al giorno d'oggi la fisica classica sono la meccanica (distinta a sua volta in più branche), la gravità (così come descritta dalla legge di gravitazione universale), la termodinamica e una buona parte dell'elettromagnetismo.
Queste teorie, nonostante non siano in grado di spiegare alcuni fenomeni, per cui occorre necessariamente fare ricorso a leggi relativistiche o quantistiche, sono considerate valide approssimazioni nel limite classico di queste ultime. In particolare, per "limite classico" si usa intendere l'approssimazione per cui non si considerino oggetti di dimensioni così piccole da costringere all'utilizzo della meccanica quantistica, oppure così veloci, o così vicine a un campo gravitazionale molto intenso, da rendere necessario l'utilizzo della relatività speciale o generale.
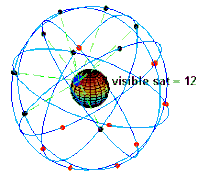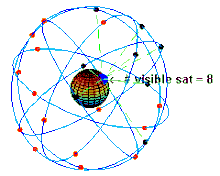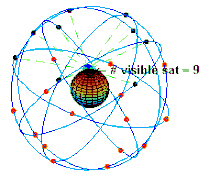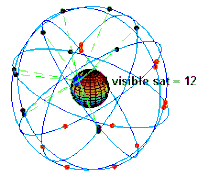
La validità dell'approssimazione al limite classico dipende tuttavia dalla precisione e dall'accuratezza che si vuole raggiungere nei calcoli e nei risultati finali. Ad esempio il GPS non sarebbe in grado di funzionare se non si considerassero gli effetti della relatività speciale e generale, sebbene il campo gravitazionale terrestre non sia intenso come quello in prossimità di un buco nero e sebbene la velocità dei satelliti artificiali in orbita sia molto minore di quella della luce.[32] Il sistema GPS richiede una precisione di sincronizzazione degli orologi dell'ordine del nanosecondo, mentre le correzioni relativistiche sono dell'ordine del microsecondo, molto piccole ma pur sempre diecimila volte maggiori rispetto all'accuratezza che si vuole raggiungere.[32] Senza queste correzioni, già dopo pochi giorni la posizione individuata dal sistema GPS sarebbe errata di decine chilometri.[32]
Meccanica classica e analitica[modifica | modifica wikitesto]

La meccanica è la scienza che studia l'equilibrio e il movimento dei corpi nello spazio, quando sottoposti a forze esterne esercitate da altri corpi.[2] Oltre alla meccanica classica è opinione di alcuni che anche la meccanica relativistica limitatamente ai risultati deducibili dalla relatività ristretta sia parte della fisica classica. La meccanica si suddivide in cinematica, dinamica e statica a seconda del tipo di studio che si vuole condurre.[2] Si parla di cinematica quando si è interessati a descrivere il moto e la sua evoluzione nel tempo e nello spazio, senza rintracciarne le cause. Quando invece si desidera studiare le cause del moto e le interazioni di vari oggetti si fa riferimento alla dinamica. Infine se si desiderano studiare le condizioni di equilibrio di un corpo si utilizzano le leggi della statica.
La cinematica è caratterizzata da una suddivisione interna basata sul tipo di moto descritto. Si parla, ad esempio, di moto rettilineo e uniforme, moto uniformemente accelerato, di moto parabolico, con ciò riferendosi alla forma traiettoria e alle leggi che regolano la mutua variazione delle quantità che descrivono il modo: posizione, velocità e accelerazione; a livello più approfondito la cinematica è studiata con gli strumenti matematici della geometria differenziale, che permettono di calcolare anche altre grandezze come il raggio di curvatura e la torsione della traiettoria.
La dinamica si basa su tre principi noti come principi della dinamica o come leggi di Newton. Essi descrivono:
- il comportamento di un corpo quando non subisce alcuna interazione;
- il comportamento di un corpo, e in particolare l'evoluzione della sua accelerazione, se sottoposto a interazioni e quindi a forze o momenti meccanici;
- la reazione del corpo a un'interazione subita.

Accanto a questi principi sono validi strumenti della dinamica anche i principi di conservazione. Questi sono comunque utilizzati generalmente in ogni settore della fisica, e vengono considerati di valenza più generale delle leggi di Newton ma trovarono la loro origine negli studi di meccanica classica. In particolare i principi di conservazione dell'energia e della quantità di moto sono i più utili negli studi dinamici e, assieme con il teorema delle forze vive permettono la descrizione e la classificazione degli urto in elastici, anelastici e completamente anelastici.
Infine, la statica si occupa di determinare le condizioni di equilibrio di un corpo, se sottoposto all'azione di altri corpi esterni. Essa studia le condizioni di equilibrio di sistemi fisici sottoposti a carichi, forze e torsioni, cioè quando il sistema non muta posizione nel tempo, o quando componenti o strutture sono a riposo. La statica è usata diffusamente nell'analisi strutturale e in scienza delle costruzioni. Per un corpo rigido le condizioni per l'equilibrio sono due: la forza risultante agente sul corpo deve essere nullo, altrimenti il centro di massa del corpo accelererebbe, così come il momento angolare totale, altrimenti il corpo ruoterebbe. Lo studio della resistenza meccanica dei materiali è anch'essa fortemente legata alla statica.

In alcuni casi, la risoluzione esplicita e diretta di sistemi di equazioni differenziali, ricavate utilizzando le leggi della dinamica, può essere semplificata mediante la ricerca delle costanti del moto, utilizzando tecniche più raffinate di meccanica razionale o di meccanica analitica basate su particolari funzioni costruite per descrivere il sistema, note come funzione lagrangiana e hamiltoniana. Nel caso del formalismo hamiltoniano si opera rinunciando all'uso delle coordinate e dei momenti (lineari o angolari) definiti dalle posizioni dei corpi e dalle loro velocità nell'ordinario spazio in tre dimensioni e utilizzando al loro posto coordinate e momenti generalizzati, definiti in uno spazio particolare, detto spazio delle fasi. Una peculiarità delle coordinate e dei momenti generalizzati è che le formule che ne descrivono le variazioni tengono già conto dei vincoli imposti al sistema, come ad esempio il vincolo di rotolare su un piano senza slittare. Pertanto tutte le condizioni imposte dai vincoli sono automaticamente rispettate dal sistema. Un concetto nato nell'ambito della meccanica razionale, ma che ha grande rilevanza in tutta la fisica, è il principio di minima azione, inteso come sinonimo sia del principio di Hamilton che del principio di Maupertuis. Questo principio stabilisce che un sistema classico evolve nel tempo in modo da minimizzare una quantità fisica, detta azione[33]. La sua applicazione permette, ad esempio, di ricavare esplicitamente le equazioni del moto a partire dall'hamiltoniana del sistema.[34]
La meccanica si suddivide anche a seconda del tipo di oggetto considerato. Considerando un corpo solido, sono due i modelli meccanici più utilizzati: il modello del punto materiale e il modello del corpo rigido. Il primo di questi è utilizzato per studiare corpi le cui parti interne e le dimensioni siano molto piccole rispetto alle altre grandezze considerate nel problema. Ad esempio nel caso si voglia studiare il moto di rivoluzione della Terra attorno al Sole, è possibile considerare in buona approssimazione l'intera Terra come se fosse puntiforme, con tutta la massa concentrata in un singolo punto. Al contrario, non è possibile approssimare uno pneumatico che rotola giù da una scarpata senza ostacoli in discesa come un punto; altrimenti i tempi di arrivo alla fine della scarpata calcolati con questa approssimazione saranno drasticamente diversi da quelli effettivamente osservati.[35][36] Ulteriori modelli che tengono conto anche delle deformazioni che un solido può subire sono oggetto di studio della meccanica del continuo, che si occupa anche dei fluidi.
Nello studio dei fluidi, la situazione è più complessa, in quanto ciascun fluido è costituito da un numero molto alto di costituenti elementari (atomi o molecole), che non possono essere considerati tra loro solidali.[37] Si deve perciò scegliere se si vuole una descrizione che tenga conto esclusivamente delle proprietà globali o se si vuole invece analizzare più nel dettaglio i comportamenti dei costituenti, rinunciando comunque a una descrizione esatta. Nel primo caso si ricorre alle leggi della fluidodinamica e della fluidostatica e ai modelli di fluido: ideale, incomprimibile, newtoniano o non newtoniano, a seconda dei valori della viscosità o della possibilità o meno di comprimere le sostanze considerate.
Se invece si vuole una descrizione più fine dei fluidi considerati, si rende necessario uno studio dal punto di vista della meccanica statistica. Quest'ultima è in grado di descrivere i comportamenti medi dei costituenti di un sistema[38], e quindi fornire gli stessi risultati ottenuti con una descrizione tipica della meccanica dei fluidi, ma è anche in grado di dare risposte su quale sia la probabilità che le variabili che descrivono un costituente assumano un certo insieme di valori. La meccanica statistica è cioè in grado di operare valutando le distribuzioni dei costituenti interni. Bisogna considerare che questo settore della meccanica fu sviluppato in modo da spiegare per altra via i fenomeni di cui si occupa la termodinamica e che, pertanto, una sua trattazione completa richiede anzitutto la comprensione delle grandezze base della termodinamica stessa.
Infine, un discorso a parte merita l'acustica, che studia in generale la generazione, la trasmissione e la ricezione di vibrazioni meccaniche, o onde sonore, nei mezzi materiali. L'acustica può essere considerata parte della fluidodinamica nel caso in cui il mezzo di propagazione sia un fluido come l'aria o l'acqua. L'equazione delle onde governa la propagazione di tutti i tipi di onde di pressione in qualsiasi mezzo (per esempio i comuni suoni in aria e le onde sismiche, cioè i terremoti).
Gravitazione universale[modifica | modifica wikitesto]

La legge della gravitazione universale è utilizzata per descrivere la mutua interazione a distanza che subiscono due corpi a causa della loro massa.[39] La descrizione secondo la fisica classica di questo fenomeno si basa o sul concetto di forza e potenziale, che trovano applicazione anche nella descrizione di tutti gli altri tipi di forza a distanza noti alla fisica classica. Il campo gravitazionale è un campo conservativo, ovvero non compie lavoro se un corpo segue un percorso chiuso, cioè se si spende tanta energia per spostare un corpo in alto lungo la verticale in prossimità della superficie terrestre, tanta se ne guadagna spostandolo in basso.[40] A causa di questa proprietà del campo è possibile associare alla forza un'energia potenziale gravitazionale.
La legge della gravitazione universale, scoperta da Newton, è oggi considerata il limite classico della relatività generale e può essere usata, insieme a molte altre leggi, per i calcoli necessari alla messa in orbita dei satelliti artificiali o nello studio del comportamento dei corpi celesti. La legge in questione stabilisce che la forza che un corpo esercita su un secondo oggetto è proporzionale al prodotto delle masse e al reciproco del quadrato della distanza fra i due.[39] La costante di proporzionalità è chiamata costante di gravitazione universale. Newton calcolò le orbite dei satelliti tramite questa legge, riottenendo le leggi di Keplero, le leggi empiriche che governano il sistema solare.[41]
Nonostante la gravità sia la più debole delle interazioni fondamentali oggi note in fisica è responsabile delle maree, frutto dell'interazione fra la luna e i mari, e del movimento dei corpi celesti come i pianeti del nostro sistema solare o come le stelle nella galassia.[39] Un'intera branca della meccanica, la meccanica celeste, si occupa proprio di questi fenomeni.
Termologia[modifica | modifica wikitesto]

La termologia studia il comportamento dei corpi nei fenomeni in cui siano coinvolto il calore,[42] combinato o meno con la produzione o l'utilizzo di lavoro. La dinamica della diffusione del calore nei corpi è dettata dalla legge sulla conduzione termica, scoperta da Joseph Fourier all'inizio del XIX secolo,[43] e dall'equazione del calore, che stabiliscono in che direzione il calore si diffonde e l'andamento della temperatura nei corpi.
La branca della termologia che studia lo scambio di calore fra corpi a temperatura diversa, le trasformazioni di calore in lavoro e viceversa, è la termodinamica, che per la sua natura è sfruttata e studiata sia in ambito fisico che chimico: in effetti, non c'è praticamente ambito della fisica al quale la termodinamica non possa essere applicata. Anche in chimica, così come in meccanica statistica, si parla di sistemi[38] proprio a causa della detta corrispondenza che esiste fra le grandezze che si studiano considerando le proprietà medie di un insieme di costituenti elementari, e che sono le grandezze termodinamiche, e le grandezze tipiche della meccanica statistica. Si deve notare che alcune grandezze tipiche della descrizione statistica (come l'entropia) non hanno un analogo macroscopico, essendo la loro definizione legata proprio alle proprietà microscopiche del sistema.[44]
La temperatura è una grandezza alla base delle misurazioni in termologia e in termodinamica, definita da quello che è chiamato il principio zero, che stabilisce che se due corpi sono in equilibrio termodinamico con un terzo corpo, allora lo sono anche fra loro.[45] In questo modo la temperatura diventa la grandezza fisica comune e uguale per tutti i corpi in equilibrio termico fra loro.
La termodinamica si basa su tre ulteriori principi che stabiliscono che:
- la variazione di energia interna di un corpo è uguale alla differenza fra il calore assorbito dal sistema (il valore è convenzionalmente negativo se il calore è ceduto dal sistema) e il lavoro compiuto dal sistema (il valore è convenzionalmente negativo se il lavoro è compiuto sul sistema);[46]
- è impossibile costruire una macchina che abbia esclusivamente l'effetto di trasferire calore da un corpo freddo a un corpo caldo;[47]
- è impossibile raggiungere lo zero assoluto utilizzando un numero finito di trasformazioni termodinamiche.[48]
Elettromagnetismo[modifica | modifica wikitesto]

L'elettromagnetismo è la branca della fisica che studia i fenomeni di natura elettrica e magnetica e le loro mutue interazioni. La moderna teoria dell'elettromagnetismo riesce a conciliare fenomeni apparentemente diversi quali i fenomeni elettrici, magnetici e l'ottica geometrica, riconducendoli a essere manifestazioni fenomenologiche del campo elettromagnetico. A seconda della tipologia di fenomeni studiati, è comunque utile suddividere lo studio dei fenomeni elettromagnetici ascrivendoli a diverse aree della teoria. La teoria può essere suddivisa differenziando tra fenomeni appartenente statici, non dipendenti dal tempo, e dinamici.
Fra i fenomeni statici quelli elettrici sono studiati dall'elettrostatica. In questa teoria gli enti fondamentali sono le cariche elettriche, positive o negative, che contemporaneamente generano e subiscono gli effetti del campo elettrico. Le cariche elettriche interagiscono secondo la legge di Coulomb: oggetti con la carica elettrica di segno opposto subiscono una forza attrattiva, mentre cariche dello stesso segno si respingono. L'intensità della forza elettrostatica che si origina fra i due corpi è proporzionale al prodotto delle cariche e inversamente proporzionale al quadrato della distanza fra i due. La costante di proporzionalità è chiamata costante di Coulomb ed è proporzionale all'inverso della costante dielettrica del vuoto.[49]

In elettrostatica il campo elettrico è definito punto per punto, in modo analogo al campo gravitazionale, dalla forza elettrica che un corpo subisce per unità di carica
- ,
nel limite in cui la carica sia abbastanza piccola da non disturbare le altre sorgenti cariche che generano il campo elettrico.[50]
Il campo elettrico è conservativo, questo significa che non compie lavoro su di un corpo se questo corpo si sposta tornando al punto di partenza, muovendosi lungo un percorso chiuso. Ad esempio un corpo carico negativamente guadagna tanta energia cinetica avvicinandosi alla sorgente positiva del campo, quanta ne perderà spostandosi nel verso opposto fino al punto di partenza.[40] A causa di questa proprietà del campo è possibile associare alla forza un'energia potenziale elettrica.[51]
In elettrostatica riveste particolare importanza l'equazione di continuità della carica elettrica, che afferma che la quantità carica elettrica non si può né creare né distruggere, ma può solo trasferirsi da un corpo all'altro. Un altro importante teorema è il teorema del flusso, che si può definire anche per il campo gravitazionale, che fornisce un legame tra il flusso del campo elettrico attraverso una superficie chiusa e la carica contenuta all'interno.
I fenomeni magnetici stazionari sono invece studiati dalla magnetostatica. Il campo magnetico è generato da correnti, ovvero da cariche in movimento, come affermato dalla legge di Biot-Savart. Al contrario del caso elettrostatico, il campo magnetico non è conservativo. Inoltre, non vi è alcune evidenza sperimentale circa l'esistenza del monopolo magnetico isolato, l'equivalente di una carica elettrica isolata:[52] le due polarità magnetiche si presentano sempre accoppiate e il campo generato per questo motivo è detto solenoidale.[53] In magnetostatica si osserva che, analogamente a quanto accade in elettrostatica, poli magnetici uguali si respingono e poli magnetici opposti si attraggono. Sulla base di questo principio, e sulla base del fatto che la Terra possiede un proprio campo magnetico, si basa il funzionamento della bussola, inoltre è per questa ragione che le due polarità magnetiche sono chiamate "nord" e "sud".[54]

La legge di Lorentz descrive l'azione del campo magnetico sulle cariche elettriche. A differenza di quella elettrica, quest'ultima forza non compie lavoro e quindi non modifica il modulo della velocità con cui si muovono le cariche, ma ne può modificare la direzione e il verso. Questo è il motivo per cui negli acceleratori di particelle i campi magnetici sono utilizzati per mantenere la direzione del fascio di particelle, o per deviarlo, mentre i campi elettrici sono intervallati in brevi regioni per accelerare le particelle.
Una descrizione classica del magnetismo nella materia sfrutta le correnti amperiane, deboli correnti che si generano su scale molto piccole, per schematizzare gli effetti di magnetizzazione, in modo analogo agli effetti della polarizzazione elettrica. Il comportamento dei materiali sottoposti a un campo magnetico varia a seconda delle loro caratteristiche chimico-fisiche, potendo variare da un estremo di minimo effetto (come ne materiali diamagnetici e paramagnetici) a un effetto molto pronunciato (come nei materiali ferromagnetici).
L'unione di elettricità e magnetismo è sintetizzata dalle quattro equazioni di Maxwell. Campi elettrici e campi magnetici sono due aspetti di uno stesso fenomeno: in particolare, se viene meno la condizione di stazionarietà, cioè se uno dei campi varia nel tempo, la variazione di uno induce l'altro.[55][56] Inoltre, cade anche il concetto di interazione a distanza fra particelle cariche, introdotto originariamente dalla legge di Coulomb, ogni particella carica interagisce infatti solo con il campo elettromagnetico localmente come descritto dalla legge di Lorentz.
Le equazioni di Maxwell hanno come soluzione nel vuoto un'onda che viaggia alla velocità della luce.[56] L'elettromagnetismo classico contiene quindi anche una teoria ondulatoria della luce, la quale viene descritta come onda elettromagnetica, caratterizzata da un preciso spettro di frequenze. Sono in questo modo ricondotti nell'ambito dell'elettromagnetismo classico anche i fenomeni dell'ottica fisica, come la diffrazione.
In formule[modifica | modifica wikitesto]
La fisica classica e i fenomeni da essa previsti possono essere riassunti da alcune formule principali:[57]
- Legge della gravitazione universale:
- Legge di Lorentz:
- Equazioni di Maxwell (nel vuoto):
- Conservazione della carica[60]:
Nelle formule i simboli sono usati per rappresentare quantità fisiche scalari o vettoriali (queste ultime in grassetto):
- il vettore forza;
- il vettore quantità di moto;
- il tempo;
- il vettore velocità totale relativa tra l'oggetto e l'osservatore;
- il fattore di Lorentz;
- la velocità della luce nel vuoto che è una costante universale;
- la costante di gravitazione universale;
- e sono le masse dei due corpi;
- un versore diretto dal corpo 1 al corpo 2;
- la distanza tra i baricentri dei corpi;
- il simbolo rappresenta l'operatore nabla;
- e rispettivamente gli operatori differenziali divergenza e rotore espressi tramite l'operatore nabla;
- il vettore flusso della densità di corrente;
- la densità di carica;
- il vettore campo elettrico;
- il vettore campo magnetico;
- le costanti e rispettivamente la costante dielettrica del vuoto e la permeabilità magnetica del vuoto, e sono legate dalla relazione ;
- la carica elettrica.
Queste formule si applicano nel rispetto del principio di relatività galileiano[61], del principio di conservazione della massa e della proporzionalità tra massa inerziale e gravitazionale che sono sottintesi come cardini costitutivi dell'intera fisica classica.
Note[modifica | modifica wikitesto]
- ^ La relatività ristretta (pubblicata nel 1905) viene generalmente inclusa nella fisica classica, si veda, per esempio, Richard Feynman.
- ^ a b c d meccanica, su treccani.it, treccani. URL consultato il 22 febbraio 2015.
- ^ eclissi, su treccani.it. URL consultato il 6 febbraio 2016.
- ^ La nascita della scienza nel periodo Ellenistico, su fisicamente.net. URL consultato il 5 novembre 2008.
- ^ a b c d e f g h i j Fisica, su treccani.it. URL consultato il 10 maggio 2016.
- ^ Nel Dialogo sui massimi sistemi, Simplicio, strenuo difensore della dottrina aristotelica, afferma:
«Non avete, primieramente, che oltre alle tre dimensioni non ve n'è altra, perché il tre è ogni cosa, e 'l tre è per tutte le bande? e ciò non vien egli confermato con l'autorità e dottrina de i Pittagorici, che dicono che tutte le cose son determinate da tre, principio, mezo e fine, che è il numero del tutto? E dove lasciate voi l'altra ragione, cioè che, quasi per legge naturale, cotal numero si usa ne' sacrifizii degli Dei? e che, dettante pur così la natura, alle cose che son tre, e non a meno, attribuiscono il titolo di tutte?»
Salviati, sostenitore del metodo scientifico, risponde:
«Meglio dunque era lasciar queste vaghezze a i retori e provar il suo intento con dimostrazione necessaria, ché così convien fare nelle scienze dimostrative.»
- ^ Antonio Favaro, Galileo Galilei, 1939.
- ^ G. B. Airy, Account of some circumstances historically connected with the discovery of the planet exterior to Uranus, in Monthly Notices of the Royal Astronomical Society, vol. 7, 13 novembre 1846, pp. 121–144, Bibcode:1846MNRAS...7..121A, DOI:10.1002/asna.18470251002.
- ^ Albert Einstein, p. 18.
- ^ Albert Einstein, p. 21.
- ^ Max Planck, Ueber die Elementarquanta der Materie und der Eletricität, in Annalen der Physik, vol. 2, 1900, p. 564.
- ^ a b c d (EN) Modern Atomism, su plato.stanford.edu. URL consultato il 10 febbraio 2016.
- ^ (EN) David Z. Albert, The logical structure of Newtonian mechanics, su britannica.com. URL consultato il 12 febbraio 2015.
- ^ Galileo Galilei, Dialogo sopra i due massimi sistemi del mondo
- ^ V.I. Arnol'd, Mathematical Methods of Classical Mechanics, springer, 1989, pp. 3-4.
- ^ Albert Einstein, p. 17.
- ^ Albert Einstein, pp. 21-22.
- ^ (EN) determinism, su britannica.com.
- ^ (FR) Pierre Simon Laplace, Essai philosophique sur les probabilités, Parigi, Bachelier, 1825, pp. 3-4.
- ^ (EN) Causal Determinism, su plato.stanford.edu.
- ^ (EN) Henk Bos, Mathematics and Rational Mechanics, in G. S. Rousseau e R. Porter (a cura di), The Ferment of Knowledge: Studies in the Historiography of Eighteenth Century Science, New York, Cambridge University Press, 1980, ISBN 0-521-22599-X.
- ^ (EN) Harald Iro, 15, in A Modern Approach to Classical Mechanics, World Scientific, 2002.
- ^ Ad esempio i famosi metodi di Runge-Kutta furono sviluppati alla fine del 1800, (DE) C. Runge, Ueber die numerische Auflösung von Differentialgleichungen, in Math. Ann., n. 46, 1895, pp. 167–178. e (DE) W. Kutta, Beitrag zur naherungsweisen Integration von Differentialgleichungen, in Z. Math. und Phys., n. 46, 1901, pp. 435–453.
- ^ a b Massimo Bonavita, Effetto farfalla, su treccani.it.
- ^ Questo concetto viene espresso dal principio di indeterminazione di Heisenberg.
- ^ Fanno eccezione una minoranza di casi in cui il vettore di stato è un autostato dell'operatore quantistico che descrive l'interazione.
- ^ In particolare, l'esperimento della doppia fenditura è interpretabile se si assume che ciascun elettrone possieda sia proprietà di una particella che quelle di onda e passi quindi da entrambe le fenditure praticate su uno schermo posto sul suo cammino. Ponendo una lastra fotografica ad una certa distanza e facendo passare numerosi elettroni è possibile osservare una figura di diffrazione nonostante si sia fatto passare un solo elettrone alla volta, mostrando chiaramente la natura ondulatoria dell'elettrone.
- ^ Einstein stesso propose che il non determinismo della teoria quantistica fosse spiegabile con una teoria alternativa che richiedesse la presenza di variabili nascoste, ossia grandezze ignote che, pur non essendo misurabili, avrebbero reso deterministico il comportamento del sistema. Nel 1965 lo scienziato John Stewart Bell mostrò che una teoria a variabile locali nascoste, come quella proposta da Einstein, dovesse soddisfare una serie di relazioni note come disuguaglianze di Bell. Alcuni esperimenti effettuati successivamente, ed in particolare nel 1980 da Alain Aspect, evidenziarono una violazione della disuguaglianza di Bell sancendo definitivamente il carattere non deterministico della teoria quantistica.
- ^ atomismo, su treccani.it. URL consultato il 10 febbraio 2016.
- ^ (EN) May 1801: Thomas Young and the Nature of Light, su aps.org. URL consultato il 10 febbraio 2016.
- ^ (DE) Albert Einstein, Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen (PDF), in Annalen der Physik, vol. 322, n. 8, May 1905, pp. 549–560, Bibcode:1905AnP...322..549E, DOI:10.1002/andp.19053220806. URL consultato il 10 febbraio 2016 (archiviato dall'url originale il 18 luglio 2007).
- ^ a b c (EN) Real-World Relativity: The GPS Navigation System, su astronomy.ohio-state.edu. URL consultato il 22 febbraio 2015.
- ^ Il principio di minima azione, unitamente al formalismo lagrangiano e hamiltoniano, è infatti estendibile anche alla teoria della relatività e alla meccanica quantistica.
- ^ AZIONE MINIMA, principio dell', su treccani.it. URL consultato il 4 maggio 2016.
- ^ Una sfera ed un cilindro cavo rotolano su un piano inclinato, su matematicaescuola.it.
- ^ Giro della morte per un corpo che rotola (PDF), su online.scuola.zanichelli.it.
- ^ In realtà anche le particelle dei solidi sono in continuo movimento, in quanto subiscono dei moti vibrazionali rispetto alle loro posizioni su un reticolo tridimensionale, ma dal punto di vista macroscopico possono essere considerate fisse rispetto al baricentro del corpo, mentre le particelle di un gas sono in movimento sia dal punto di vista microscopico che macroscopico, in quanto non sono vincolate a nessun reticolo.
- ^ a b La meccanica statistica non si limita allo studio dei fluidi, ma può studiare qualunque insieme costituito da un numero molto alto di costituenti che siano almeno in mutua interazione fra loro. Si parla in questo caso genericamente di sistema per riferirsi tanto ai costituenti quanto a eventuali altri corpi in interazione diretta con questi.
- ^ a b c La legge della gravitazione universale, su sapere.it.
- ^ a b Da un punto di vista matematico dire che un campo è conservativo significa che la sua circuitazione lungo una linea chiusa è nulla oppure che il rotore del campo è nullo in qualsiasi punto del dominio di esistenza.
- ^ Effetti relativistici comportano deviazioni significative dalle orbite previste dalla teoria di Newton soprattutto in riferimento a Mercurio.
- ^ Termologia, su sapere.it.
- ^ Joseph Fourier, Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, 1822.
- ^ Le grandezze senza analogo macroscopico in meccanica statistica possono in alcuni casi particolari essere comunque misurate indirettamente a partire da altre grandezze macroscopiche.
- ^ (EN) Thermal Equilibrium, su hyperphysics.phy-astr.gsu.edu. URL consultato il 17 settembre 2015.
- ^ Le convenzioni sui segni di calore e lavoro nella formulazione del primo principio della termodinamica possono essere differenti dalla convenzione citata. In ogni caso qualsiasi sia la convenzione adottata, purché se ne adotti una consistente, la validità del principio non è inficiata.
- ^ Vi sono più enunciazioni del secondo principio della termodinamica, e tutte sono equivalenti fra loro. In questo caso è riportato l'enunciato di Rudolf Clausius
- ^ Solitamente questo principio viene presentato come una diretta conseguenza del precedente.
- ^ Jackson, p. 1.
- ^ Jackson, p. 2.
- ^ Il potenziale elettrico, su sapere.it. URL consultato il 5 febbraio 2016.
- ^ (EN) The search for the magnetic monopole, su moedal.web.cern.ch. URL consultato il 14 febbraio 2015 (archiviato dall'url originale il 14 febbraio 2015).
- ^ Da un punto di vista matematico dire che un campo è solenoidale significa che il suo flusso attraverso una superficie chiusa è nullo oppure che la divergenza del campo è nulla in qualsiasi punto del dominio di esistenza.
- ^ Proprietà magnetiche della materia, su sapere.it. URL consultato il 5 febbraio 2016.
- ^ Con riferimento alla variazione dei campi elettrico e magnetico, più precisamente, si osserva che questi inducono una variazione del rotore, o del flusso, dell'altro campo. Per questo motivo si può parlare di flusso indotto riferendosi a questo processo.
- ^ a b (EN) Alok Jha, What are Maxwell's Equations?, su theguardian.com.
- ^ Richard Feynman, volume 2, tabella 18-1.
- ^ Isaac Newton enunciò la seconda legge nel seguente modo:
(LA) Isaac Newton, Philosophiae naturalis principia mathematica, Londra, Samuel Pepys, 1687.(LA)
«Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.»
(IT)«L'alterazione del moto è sempre proporzionale alla forza motrice impressa e avviene lungo la linea retta nella quale la forza è impressa.»
- ^ La correzione imposta dalla relatività ristretta si applica alla fisica classica solo se si condivide l'ipotesi che questa teoria sia effettivamente classica e non moderna.
- ^ Questa formula può comunque essere derivata dalla quarta equazione di Maxwell applicando l'operatore divergenza ad entrambi i membri.
- ^ Nel caso in cui si consideri la relatività speciale come teoria classica si deve considerare il principio di relatività speciale.
Bibliografia[modifica | modifica wikitesto]
- Sigfrido Boffi, Risultati di fisica classica, in Da Laplace a Heisenberg (PDF), Pavia, La goliardica pavese, 1996, ISBN 88-7830-170-1. URL consultato il 29 settembre 2008.
- Alessandro Braccesi, Una storia della fisica classica, Bologna, Zanichelli, 1992, ISBN 88-08-11334-5.
- Albert Einstein e Leopold Infeld, L'evoluzione della fisica, traduzione di Adele Graziadei, Torino, Bollati Boringhieri, 1965, ISBN 88-339-0025-8.
- Albert Einstein, Autobiografia scientifica, Tradotto da Augusto Gamba, Torino, Bollati Boringhieri, 1979, ISBN 978-88-339-0362-0.
- Richard Feynman, La fisica di Feynman, traduzione di Simone Franchetti sotto il coordinamento di Giuliano Toraldo di Francia, Bologna, Zanichelli, 2001, ISBN 88-08-05179-X.
- Hal Hellman, Le dispute della scienza, traduzione di Pietro Adamo, Milano, Raffaello Cortina Editore, 1999, ISBN 88-7078-600-5.
- (EN) John David Jackson, Classical Electrodynamics, John Wiley & Sons, 1962.
- Roger Penrose, La strada che porta alla realtà, traduzione di Emilio Diana, Milano, BUR, 2006, ISBN 88-17-01233-5.
- Paolo Rossi, La nascita della scienza moderna in europa, Bari, Laterza, 2000 [1997], ISBN 88-420-6120-4.
Voci correlate[modifica | modifica wikitesto]
- Generali
- Branche
Altri progetti[modifica | modifica wikitesto]
 Wikibooks contiene un libro sulla fisica classica
Wikibooks contiene un libro sulla fisica classica Wikiversità contiene risorse sulla fisica classica
Wikiversità contiene risorse sulla fisica classica
Collegamenti esterni[modifica | modifica wikitesto]
- Rivista di fisica, su fisicamente.net. URL consultato il 2 novembre 2008 (archiviato dall'url originale il 13 settembre 2008). in cui è contenuta una sezione sulla storia della fisica.
- Animazioni di fisica classica, su polimi. URL consultato il 14 agosto 2016 (archiviato dall'url originale il 19 novembre 2011).
- (EN) HyperPhysics, su hyperphysics. URL consultato il 14 agosto 2016. Un ambiente di esplorazione dei concetti della fisica (classica e moderna) strutturato come una mappa concettuale.
- (EN) Motion Mountain: The adventure of physics, su onlinefreeebooks.net. URL consultato il 2 novembre 2008 (archiviato dall'url originale il 20 novembre 2008).
| Controllo di autorità | GND (DE) 4711777-1 |
|---|




























