Diffrazione

La diffrazione, nella fisica, è un fenomeno associato alla deviazione della traiettoria di propagazione delle onde quando queste incontrano un ostacolo sul loro cammino. È tipica di ogni genere di onda, come il suono, le onde sulla superficie dell'acqua o le onde elettromagnetiche come la luce o le onde radio; il fenomeno si verifica anche nelle particolari situazioni in cui la materia mostra proprietà ondulatorie, in accordo con il dualismo onda-particella.
Gli effetti di diffrazione sono rilevanti quando la lunghezza d'onda è comparabile con la dimensione dell'ostacolo: in particolare per la luce visibile (lunghezza d'onda attorno a 0,5 µm) si hanno fenomeni di diffrazione quando essa interagisce con oggetti di dimensione sub-millimetrica.
Storia[modifica | modifica wikitesto]


Qualunque deviazione di un raggio di luce non imputabile a riflessione o rifrazione è chiamato diffrazione. Questa è la classica definizione riscontrata nel trattato classico di Ottica di Arnold Sommerfeld[1]. È sorprendente notare che questa definizione ricalca quanto descritto per la prima volta dal Gesuita Francesco Maria Grimaldi (si veda l'originale definizione nella seconda figura che riproduce l'originale paragrafo nel trattato di F. M. Grimaldi), coniandone il termine che significa "frazionamento in più parti" nel 1665[2]. Isaac Newton attribuì la causa del fenomeno a un incurvamento dei raggi luminosi (non osservando, come tutti gli ottici newtoniani, le frange all'interno dell'ombra di un capello)[3].
Il termine newtoniano che designa la diffrazione è inflexion. Thomas Young studiò la diffrazione come sovrapposizione tra la luce direttamente trasmessa oltre un'apertura in uno schermo (o un ostacolo) e un'onda avente origine dal bordo dell'apertura o dell'ostacolo. Lo stesso Augustin-Jean Fresnel adottò inizialmente il modello di Thomas Young, ma alcune esperienze atte ad evidenziare variazioni della figura di diffrazione dai parametri caratteristici del bordo (natura, geometria del bordo) e una inversione rispetto alla posizione prevista delle frange scure nella regione esterna all'ombra di un capello, lo indussero ad un abbandono della teoria dell'onda di bordo (stabilita da A. Fresnel in modo del tutto indipendente da Thomas Young), a favore della teoria basata sul principio di Huygens, riuscendo soprattutto a fornire una descrizione del fenomeno dal punto di vista matematico.
È da notare che la teoria dell'onda di bordo di Thomas Young ha precursori "newtoniani" antecedenti a Thomas Young, la cui teoria è in alcuni punti non chiara e priva di supporto matematico. In genere la posizione di Thomas Young, cui si attribuisce il merito di avere per primo stabilito la natura periodica della luce, è in realtà incerta (il termine "lunghezza d'onda" non è mai usato) mentre è una costante delle sue ricerche l'analogia tra "suono" e "luce". Tuttavia, almeno all'epoca dei pionieri (T. Young e A. Fresnel) né la teoria dell'onda di bordo, né il principio di Huygens hanno un supporto teorico[4][5] che giunge solo nel 1883 ad opera di G. Kirchhoff[6] e, anche se inosservato, da G. A. Maggi[7] nel 1886 per la teoria dell'onda di bordo.
Generalità[modifica | modifica wikitesto]
Caratteristiche qualitative della diffrazione[modifica | modifica wikitesto]
Di fronte ad un fenomeno di diffrazione, nel caso ottico, si possono compiere alcune osservazioni preliminari. Il caso generale del fenomeno è la diffrazione di Fresnel (o da campo vicino), dove la sorgente di luce e il piano di osservazione sono posti a distanza finita dalla fessura. La diffrazione di Fraunhofer (o da campo lontano), invece, è un caso particolare della precedente, ma molto più semplice da analizzare: essa si ha infatti quando la sorgente e il piano sono posti a distanza infinita dal diaframma, così che i raggi incidenti possano essere considerati paralleli fra loro. Un esempio di questo caso è quello di una sorgente di luce puntiforme (o rettilinea), come il tratto diritto del filamento di una lampadina o un fascio laser, vista da una distanza di un paio di metri attraverso due lamette distanti tra loro mezzo decimo di millimetro. Le caratteristiche della diffrazione sono quindi che:
- la larghezza del massimo centrale della figura di diffrazione della fenditura singola è il doppio delle frange laterali.
- la larghezza è inversamente proporzionale all'ampiezza della fenditura: a fessure molto piccole corrispondono frange di diffrazione molto larghe e viceversa.
- gli angoli sotto cui le frange sono viste, non dipendono dalla scala dell'esperimento, ma solo dal rapporto tra la lunghezza d'onda e l'ampiezza della fenditura.
- in qualunque fenomeno di Fresnel, un ostacolo simmetrico presenta sempre luce al centro dell'ombra (è il tipico caso della "macchia di Poisson").
Esempi di diffrazione[modifica | modifica wikitesto]

Fenomeni di diffrazione possono essere osservati quotidianamente, in particolare quelli che interessano la luce visibile: per esempio, le tracce incise sulla superficie di un CD o di un DVD agiscono come un reticolo di diffrazione, creando il familiare effetto arcobaleno; anche i piccoli ologrammi, ad esempio delle carte di credito, si basano sulla diffrazione. In natura, si possono osservare colori cangianti dovuti a diffrazioni interferenziali, come quelli delle piume del pavone, o della corazza di alcuni coleotteri, o delle ali di molte farfalle, che sono colorate grazie all'interferenza delle onde diffratte da parte di microscopiche scaglie disposte regolarmente.

La diffrazione atmosferica causata da microscopiche gocce d'acqua in sospensione è la responsabile degli anelli luminosi visibili attorno alle sorgenti di luce; la stessa ombra di un oggetto può mostrare deboli effetti di diffrazione sui bordi. Una figura policromatica analoga alla farfalla nella foto si osserva tra le trame di un ombrello quando si guarda una luce lontana attraverso di esse. La diffrazione costituisce un limite nella risposta di qualunque strumento ottico e pertanto riguarda varie tecnologie: essa infatti pone un limite alla risoluzione di fotocamere, videocamere, telescopi e microscopi.
A causa della diffrazione le onde marine formano figure intricate quando incrociano un piccolo ostacolo, come un faro in mare, o attraversano una apertura stretta (figura a destra), come un canale o l'ingresso di un porto.
Spiegazione del fenomeno[modifica | modifica wikitesto]
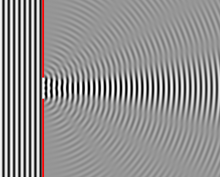
La diffrazione può venire intuitivamente "letta" come una richiesta di continuità da parte del fronte d'onda che subisce una discontinuità dal bordo (o dai bordi) di un ostacolo. La figura a fianco, che simula la diffrazione di un'onda piana attraverso la fenditura, ricorda quanto osservato in un'onda alla superficie dell'acqua quando passa attraverso una fenditura. Oltre la fenditura il fronte d'onda incidente è "tagliato" dai due bordi. La parte di fronte d'onda contigua a ciascun bordo piega attorno al bordo stesso fornendo così una perturbazione continua. Secondo la chiave di lettura della teoria dell'onda di bordo è come se l'ostacolo diventasse una sorgente (fittizia) di un'onda a simmetria cilindrica che si sovrappone tanto all'onda trasmessa secondo le leggi dell'ottica geometrica e, ovviamente, all'altra onda di bordo. Secondo la chiave di lettura del principio di Huygens, il fronte d'onda incidente è l'inviluppo di onde elementari sferiche. Qui, le sorgenti (fittizie) di tali onde sono nei punti della fenditura. L'inviluppo di tali onde sferiche in prossimità del bordo si propaga dando luogo a nuovi fronti d'onda successivi. Nonostante la diversità nella descrizione del fenomeno, sia il modello dell'onda di bordo che il modello basato sul principio di Huygens sono pienamente equivalenti visto che la "matematizzazione" della teoria dell'onda di bordo discende dalla matematizzazione della teoria della propagazione secondo il principio di Huygens.[6][7]
Descrizione matematica della diffrazione[modifica | modifica wikitesto]
Per determinare gli effetti della diffrazione bisogna trovare innanzitutto la fase e l'intensità di ciascuna sorgente di Huygens in ogni punto dello spazio; ciò significa calcolare per ogni punto la sua distanza dal fronte d'onda: se la distanza di ciascun punto differisce a meno di un numero intero di lunghezze d'onda, tutte le sorgenti sono in fase e daranno luogo ad una interferenza costruttiva; se, al contrario, la distanza differisce di un numero intero più mezza lunghezza d'onda, l'interferenza sarà distruttiva. In generale, è sufficiente determinare le posizioni di questi massimi e minimi per ottenere una completa descrizione del fenomeno.
La descrizione più semplice di diffrazione si ha nel caso di un problema in due dimensioni, come nel caso delle onde nell'acqua che si propagano solo sulla superficie del liquido; per quanto riguarda i raggi luminosi, si può trascurare una dimensione solo se la fenditura si estende in quella direzione per una distanza molto più grande della lunghezza d'onda della luce; nel caso di fenditure circolari, invece, si devono considerare tutte e tre le dimensioni.
Analisi quantitativa della diffrazione da una singola fenditura[modifica | modifica wikitesto]
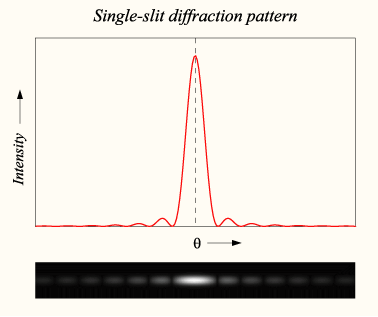

Come esempio, si può ricavare un'equazione più precisa che leghi l'intensità delle bande di diffrazione all'angolo a cui si considerano, nel caso di una singola fenditura: partendo dalla rappresentazione matematica del principio di Huygens si considera un'onda monocromatica sul piano complesso di lunghezza d'onda λ incidente su una fenditura di ampiezza a; se questa fenditura giace lungo il piano individuato dagli assi x′-y′ (con centro nell'origine), si può ipotizzare che la diffrazione generi un'onda complessa che viaggia lungo una direzione radiale r rispetto alla fenditura e la cui equazione è:
Sia ora (x′,y′,0) un punto interno alla fenditura: se (x,0,z) sono le coordinate alle quali corrisponde l'intensità da misurare della figura di diffrazione, la fenditura si estenderà da a in un verso e da a nell'altro.
La distanza r dalla fenditura è:
Considerando il caso della diffrazione di Fraunhofer, risulterà che:
In altre parole, la distanza dello schermo è molto più grande dell'ampiezza della fenditura; con l'aiuto del teorema binomiale, questa distanza può essere ben approssimata come:
Sostituendo questo valore di r nella prima equazione si trova:
Per semplificare si possono raccogliere i termini costanti e chiamarli C (C può contenere numeri immaginari, anche se al termine ψ si potrà semplificare eliminando queste componenti). Ora, nella diffrazione di Fraunhofer è molto piccolo, in modo da poter scrivere . Quindi, essendo , risulterà:
Si può notare con l'aiuto della formula di Eulero che e :
con la posizione: .
Infine, sostituendo in , l'intensità delle onde diffratte a un dato angolo θ è data da:
Analisi quantitativa della diffrazione da N fenditure[modifica | modifica wikitesto]


Ripartendo dal principio di Huygens
si considerano ora N fenditure di uguale ampiezza (a, , 0) distanti l'una dall'altra di una lunghezza d lungo l'asse x′. Come precedentemente trovato, la distanza r dalla prima fenditura sarà:
Per generalizzare questa situazione nel caso di N fenditure, si può innanzitutto osservare che mentre z e y restano costanti, x′ varia in questo modo:
Dunque si ha che:
e la somma di tutti gli N contributi all'onda è:
Di nuovo si può notare che è trascurabile, in modo che ; quindi risulta:
Ora si può usare la seguente identità
per sostituire nell'equazione e ottenere:
Di nuovo, sostituendo k e introducendo la variabile al posto delle costanti non oscillanti, come nella diffrazione da una fenditura, si può semplificare il risultato; ricordandosi che:
si possono scartare gli esponenziali e ottenere:
Diffrazione da un'apertura circolare[modifica | modifica wikitesto]


La diffrazione di un'onda piana incidente su un'apertura circolare dà come risultato il cosiddetto disco di Airy. La variazione dell'intensità dell'onda in funzione dell'angolo è data dall'espressione:
dove a è il raggio dell'apertura, k è pari a 2π/λ e J1 è una funzione di Bessel. Più piccola è l'apertura, più grande è la dispersione delle onde, a pari distanza.
Altri casi di diffrazione[modifica | modifica wikitesto]
Limite di diffrazione per i telescopi[modifica | modifica wikitesto]

Nel caso della diffrazione da un'apertura circolare, si rilevano una serie di anelli concentrici attorno al disco di Airy. L'analisi matematica di questo specifico caso è simile alla versione utilizzata per la diffrazione da una singola fenditura vista precedentemente.
Un'onda non deve necessariamente attraversare una fenditura per andare incontro a diffrazione: per esempio, anche un raggio di luce di ampiezza finita subisce un processo di diffrazione e aumenta la propria ampiezza. Questo fenomeno limita l'ampiezza d dei dispositivi dove si raccoglie la luce, nel fuoco di una lente; ciò è conosciuto come limite di diffrazione:
dove λ è la lunghezza d'onda della luce, f è la distanza focale della lente e a è il diametro del raggio di luce o (se il raggio di luce è più ampio della lente) il diametro della lente. L'ampiezza risultante contiene circa il 70% dell'energia della luce e corrisponde al raggio del primo minimo del disco di Airy, approssimato con il criterio di Rayleigh; il diametro del primo minimo, che contiene l'83.8% dell'energia della luce, è spesso utilizzato come "diametro di diffrazione".
Utilizzando il principio di Huygens, è possibile ricavare la superficie di diffrazione di un'onda che attraversa una fenditura di qualsiasi forma: se questa superficie viene osservata ad una certa distanza dall'apertura, risulterà essere la trasformata di Fourier in due dimensioni della funzione che rappresenta l'apertura.
Diffrazione di Bragg[modifica | modifica wikitesto]

La diffrazione da numerose fenditure descritta precedentemente è un fenomeno simile a ciò che si verifica quando un'onda viene diffusa da una struttura periodica, come il reticolo di atomi in un cristallo o le grate di un reticolo di diffrazione Ogni punto di diffusione, ad esempio ogni atomo del cristallo, agisce come una sorgente puntiforme di onde sferiche, le quali daranno luogo a fenomeni di interferenza costruttiva per formare un certo numero di onde diffratte. La direzione di queste onde è descritta dalla Legge di Bragg:
dove λ è la lunghezza d'onda, d è la distanza tra ogni punto di diffusione, θ è l'angolo di diffrazione e m è un numero intero che indica l'ordine di ciascun onda diffratta.
La diffrazione di Bragg viene usata nella cristallografia a raggi X per ricavare la struttura di un qualsiasi cristallo analizzando gli angoli ai quali i raggi X vengono diffratti dal cristallo stesso: poiché l'angolo θ di diffrazione dipende dalla lunghezza d'onda λ, un reticolo di diffrazione causa una dispersione angolare di un raggio di luce.
L'esempio più semplice di diffrazione di Bragg è lo spettro di colori che si può vedere riflesso da un Compact disc: la breve distanza tra le tracce sulla superficie del disco costituisce un reticolo di diffrazione e ogni componente della luce bianca viene diffratta con differenti angoli, in accordo con la legge di Bragg.
Diffrazione di particelle[modifica | modifica wikitesto]
La diffrazione di particelle materiali come gli elettroni è uno dei maggiori punti di forza della meccanica quantistica: osservare la diffrazione di un elettrone o di un neutrone consente di verificare l'esistenza della dualità onda-particella; questa diffrazione è anche un utile strumento scientifico: la lunghezza d'onda di queste particelle è sufficientemente piccola da essere usata nella scansione della struttura atomica dei cristalli.
La lunghezza d'onda associata ad una particella è la cosiddetta lunghezza d'onda di De Broglie:
dove h è la costante di Planck e v e m sono rispettivamente la velocità e la massa della particella; λ è caratteristica di qualsiasi oggetto materiale, anche se è rilevabile solo per entità con piccola massa, come gli atomi e altre particelle.
Recentemente, è stata osservata la diffrazione di particelle chiamate barioni e di un particolare tipo di fullereni chiamato buckyball ; il prossimo obiettivo della ricerca sarà quello di osservare la diffrazione dei virus, i quali, avendo molta più massa delle particelle elementari, hanno una lunghezza d'onda inferiore, cosicché devono attraversare molto lentamente una fenditura estremamente sottile affinché manifestino caratteri ondulatori.
Persino la Terra ha una sua lunghezza d'onda (in effetti, qualunque oggetto dotato di una quantità di moto la possiede): avendo una massa di circa 6×1024 kg e una velocità orbitale media di circa 30000 ms−1, essa ha una lunghezza d'onda di De Broglie pari a 3.68×10−63 m.
La coerenza[modifica | modifica wikitesto]
La descrizione della diffrazione poggia, come detto in precedenza, sulla descrizione dell'interferenza tra onde generate dalla stessa sorgente che percorrono direzioni differenti, partendo dal medesimo punto; in questo modello, la differenza di fase tra le onde dipende solo dall'effettiva lunghezza del tragitto; può accadere però che due onde emesse in tempi diversi dalla sorgente arrivino sullo schermo in due punti diversi ma allo stesso istante; la fase iniziale con cui la sorgente genera le onde può anche cambiare nel tempo: onde emesse a intervalli di tempo sufficientemente lunghi non potranno quindi formare una stabile figura d'interferenza, dal momento che la loro differenza di fase non sarà più indipendente dal tempo.
La lunghezza correlata alla fase di un'onda elettromagnetica come la luce è detta lunghezza di coerenza: affinché si verifichi un'interferenza, la differenza dei tragitti di due onde deve essere inferiore alla lunghezza di coerenza.
Se le onde sono emesse da una sorgente estesa, ciò può produrre un'incoerenza lungo la direzione trasversale: osservando perpendicolarmente un raggio di luce, la lunghezza per la quale le fasi sono correlate è chiamata lunghezza di coerenza trasversale; nel caso della diffrazione dalla doppia fenditura, solo se questa lunghezza è minore della distanza tra le due aperture si osserverà il fenomeno della diffrazione.
Nel caso della diffrazione di particelle, la lunghezza di coerenza è legata all'estensione nello spazio della funzione d'onda che descrive tali particelle.
Note[modifica | modifica wikitesto]
- ^ A. Sommerfeld, Optics (Academic press, New York, 1954) p.179.
- ^ Physico-mathesis de lumine, coloribus et iride (Bonomiae, 1665).
- ^ I. Newton, Opticks, (London, 1704) Book 3.
- ^ G. N. Cantor, "Was Thomas Young a wave theorist?", Am. J. Phys. 52, 305 - 308 (1984).
- ^ S. Ganci, "Historical notes on the first viewpoint about light diffraction", Quaderni di Storia della Fisica, 13, 59 - 65 (2005).
- ^ a b G. Kirchhoff, "Zur Theorie der Lichtstrahlen", Wied. Ann. 18, 663 - 695 (1883).
- ^ a b G. A. Maggi, "Sulla Propagazione Libera e Perturbata delle Onde Luminose in um Mezzo Isotropo", Ann. Matematica, 16, 21 - 47 (1888).
Voci correlate[modifica | modifica wikitesto]
- Criterio di Rayleigh
- Diffrazione atmosferica
- Diffrazione dei raggi X
- Diffrazione dell'elettrone
- Diffrazione neutronica
- Diffrazione di Bragg
- Diffrazione di Fraunhofer
- Diffrazione di Fresnel
- Fotografia
- Interferenza (fisica)
- Numero di Fresnel
- Onda (fisica)
- Principio di Babinet
- Reticolo di diffrazione
- Teoria dinamica della diffrazione
- Zona di Fresnel
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «diffrazione»
Wikizionario contiene il lemma di dizionario «diffrazione» Wikimedia Commons contiene immagini o altri file su diffrazione
Wikimedia Commons contiene immagini o altri file su diffrazione
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) diffraction / diffraction pattern, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Wave Optics, su lightandmatter.com. URL consultato il 5 dicembre 2006 (archiviato dall'url originale il 15 gennaio 2010).
- (EN) 2-D wave java applet mostra le bande di diffrazione che si formano utilizzando diverse configurazioni di fenditure.
- (EN) Diffraction java applet mostra bande di diffrazione per fenditure di vari forme.
- (EN) Diffraction approximations illustrated sito del MIT che illustra le varie approssimazioni utilizzate nello studio della diffrazione.
- (EN) Diffraction Limited Photography spiega come i vari fenomeni di diffrazione limitino la risoluzione di ogni tipo di apparecchio ottico.
- (EN) Diffraction and acoustics., su acoustics.salford.ac.uk. URL consultato il 10 aprile 2007 (archiviato dall'url originale il 21 novembre 2009).
- (EN) Gap Obstacle Corner - Simulazioni Java della diffrazione delle onde del mare.
- (EN) Google Maps - Suggestiva immagine satellitare della diffrazione delle onde dell'oceano che entrano nel Canale di Panama.
| Controllo di autorità | Thesaurus BNCF 29404 · LCCN (EN) sh85037928 · GND (DE) 4145094-2 · BNE (ES) XX527015 (data) · BNF (FR) cb131628747 (data) · J9U (EN, HE) 987007552907505171 · NDL (EN, JA) 00564628 |
|---|












![{\displaystyle ={\frac {i\Psi ^{\prime }}{z\lambda }}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}\int _{-\infty }^{\infty }e^{-ik\left[z+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{2z}}\right]}\,dx^{\prime }\,dy^{\prime }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a91bb94c1128b4abe454dd58f5a83ce0b134410e)
![{\displaystyle ={\frac {i\Psi ^{\prime }}{z\lambda }}e^{-ikz}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{-ik\left[{\frac {\left(x-x^{\prime }\right)^{2}}{2z}}\right]}\,dx^{\prime }\int _{-\infty }^{\infty }e^{-ik\left[{\frac {y^{\prime 2}}{2z}}\right]}\,dy^{\prime }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4c2410113dd95632b38d1b26bb7ebda73467fe)









![{\displaystyle \Psi =aC{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}=aC\left[\operatorname {sinc} \left({\frac {ka\sin \theta }{2}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f79356554dbbba3ea663d9f2fa6d6aba14867908)




![{\displaystyle =I_{0}{\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a6e14c788807fa148715c2e256693db3c058a51)


















![{\displaystyle I\left(\theta \right)=I_{0}\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]^{2}\cdot \left[{\frac {\sin \left({\frac {N\pi d}{\lambda }}\sin \theta \right)}{\sin \left({\frac {\pi d}{\lambda }}\sin \theta \right)}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/817c1f8594184fc46dc4a12c31e54b59e644c4f8)



