Dipolo magnetico

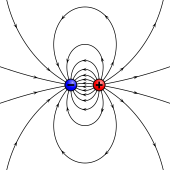
Un dipolo magnetico, nella magnetostatica, è un magnete ottenuto considerando una spira microscopica percorsa da corrente elettrica.[1] Si tratta del primo termine dell'espansione in multipoli del campo magnetico.
La grandezza che caratterizza principalmente un dipolo magnetico è il momento magnetico, che quantifica la tendenza del dipolo ad orientarsi in una data direzione in presenza di un campo magnetico esterno.
Si tratta di un modello equivalente a due cariche magnetiche opposte rigidamente connesse, in analogia con il dipolo elettrico. Si realizza diminuendo le dimensioni di una spira percorsa da corrente elettrica, mantenendone costante il momento magnetico e prendendo il limite in cui l'area della spira è nulla. Il dipolo magnetico costituisce il caso più semplice di un 2p-polo, in cui 2p è il numero di coppie polari, che per la legge di Gauss magnetica è un numero intero.
Si tratta di un'utile schematizzazione dell'influsso di un campo magnetico su spire molto piccole percorse da corrente, ed è perciò usato nell'ambito della fenomenologia del magnetismo nella materia attraverso modelli atomici classici (come quelli di Rutherford e Bohr), tramite l'introduzione di correnti atomiche dovute al moto degli elettroni e a correnti di Larmor causate dalla precessione dell'orbita di questi.
Momento magnetico[modifica | modifica wikitesto]


Prima del 1930 nei testi si definiva il momento magnetico utilizzando il concetto di "polo magnetico", in analogia con l'elettrostatica. Successivamente si è preferito considerare una spira percorsa da corrente elettrica: nel limite in cui le sue dimensioni diminuiscono mantenendo costante il prodotto tra corrente ed area si ottiene il modello per il dipolo magnetico.
Nel primo modello si può pensare ad un magnete come due poli magnetici di "carica magnetica" aventi polarità opposta e separati da una certa distanza . Il momento magnetico che si genera è direttamente proporzionale alla carica e alla distanza che separa le cariche.
Il verso della sua direzione punta inoltre dal polo sud al polo nord.
Nel secondo modello, che utilizza una spira di area percorsa da corrente , si definisce il momento magnetico come il prodotto tra area e corrente nel seguente modo:
e la direzione del vettore area segue la regola della mano destra.[2]
Nel caso più generale, il momento di una distribuzione spaziale arbitraria di corrente è dato dall'equazione:
dove è la densità di corrente relativa all'elemento di volume nel punto , con la densità di carica e la velocità, e dove è il prodotto vettoriale e la posizione. Nel sistema internazionale (SI), la dimensione del dipolo magnetico è Area×corrente elettrica, che si traduce in due notazioni equivalenti: 1 m²·A = 1 J/T.
Campo magnetico generato da un dipolo[modifica | modifica wikitesto]
Un dipolo magnetico genera un campo magnetico, descritto dal primo termine dello sviluppo in multipoli di un campo generico.
Campo esterno[modifica | modifica wikitesto]
In fisica classica il campo magnetico generato da un dipolo è calcolato considerando una spira percorsa da corrente elettrica. Nel limite in cui le sue dimensioni diminuiscono mantenendo costante il prodotto tra corrente ed area si ottiene il modello per il dipolo magnetico. Il potenziale vettore magnetico della spira è dato dall'espressione:
- ,
dove è il momento di dipolo magnetico e è la permeabilità magnetica del vuoto.
L'intensità del campo magnetico è data da:
- .
In modo equivalente si può considerare come modello di dipolo due cariche magnetiche opposte nel limite in cui la loro distanza e la loro carica diminuiscono in modo tale da mantenere il loro prodotto costante, in analogia con il dipolo elettrico. Si ottiene in questo modo il potenziale scalare magnetico:
- ,
da cui si ha che l'intensità di è:
- .
Tale campo è simmetrico rispetto alle rotazioni intorno all'asse del momento magnetico.

Campo interno[modifica | modifica wikitesto]
Il campo generato da un dipolo è modellizzabile con una spira percorsa da corrente soltanto all'esterno della regione di spazio occupata dalla sorgente. Supponendo di diminuire l'estensione spaziale della spira, il campo limite è:
dove , e l'espressione è valida all'interno del dipolo.
Se si considera il modello di dipolo che utilizza due cariche, il campo limite è:
I campi così ottenuti sono legati dalla relazione:
dove:
è il vettore di magnetizzazione.
Forze tra due dipoli magnetici[modifica | modifica wikitesto]
La forza esercitata da un momento di dipolo su un altro momento di dipolo distante dal primo può essere calcolata utilizzando la relazione:
oppure:
La forza agente su ha direzione opposta, mentre il momento meccanico è dato da:
Note[modifica | modifica wikitesto]
- ^ Encyclopedia Britannica - magnetic dipole, su britannica.com. URL consultato il 31-08-2012.
- ^ Richard P. Feynman, Robert B. Leighton e Matthew Sands, The Feynman Lectures on Physics, vol. 2, 2006, ISBN 0-8053-9045-6.
Bibliografia[modifica | modifica wikitesto]
- Tai L. Chow, Introduction to electromagnetic theory: a modern perspective, Jones & Bartlett Learning, 2006, ISBN 978-0-7637-3827-3.
- Jackson, John D., Classical Electrodynamics (3rd ed.), Wiley, 1999, ISBN 0-471-30932-X, OCLC 224523909.
- Edward P. Furlani, Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications, Academic Press, 2001, p. 140, ISBN 0-12-269951-3.
- Schill, R. A., General relation for the vector magnetic field of a circular current loop: A closer look, in IEEE Transactions on Magnetics, vol. 39, n. 2, 2003, pp. 961–967, Bibcode:2003ITM....39..961S, DOI:10.1109/TMAG.2003.808597.
Voci correlate[modifica | modifica wikitesto]
- Campo magnetico
- Dipolo elettrico
- Dipolo molecolare
- Magnete
- Momento magnetico
- Monopolo elettrico
- Polo magnetico (fisica)
- Polarizzazione magnetica
- Particella elementare
- Solenoide
- Sviluppo in multipoli
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) magnetic dipole, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.





















![{\displaystyle \mathbf {B} (\mathbf {x} )={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {n} (\mathbf {n} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {x} |^{3}}}+{\frac {8\pi }{3}}\mathbf {m} \delta (\mathbf {x} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1722a3f5c20876377dc71ad04492971cd8b5e2e4)

![{\displaystyle \mathbf {H} (\mathbf {x} )={\frac {1}{4\pi }}\left[{\frac {3\mathbf {n} (\mathbf {n} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {x} |^{3}}}-{\frac {4\pi }{3}}\mathbf {m} \delta (\mathbf {x} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/432a9d91f1ef8cb3d5da99eb9c2655b2974f8a29)






![{\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\dfrac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\dfrac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4075ddad9565bc9c8b12c5a59b5f1cb3cdb320)
