Permeabilità magnetica
In fisica, in particolare in elettromagnetismo, la permeabilità magnetica di un materiale è una grandezza fisica che esprime l'attitudine del materiale a magnetizzarsi in presenza di un campo magnetico.
La permeabilità magnetica si misura in henry al metro (H/m), equivalente a newton all'ampere quadrato (N/A2). Quasi tutti i mezzi omogenei hanno una permeabilità magnetica che può essere considerata costante, tuttavia per alcune sostanze (come ferro, cobalto, nichel) essa ha un comportamento che manifesta una certa isteresi, ovvero la permeabilità mostra una dipendenza dalle precedenti magnetizzazioni e smagnetizzazioni subite da tali materiali. Le sostanze per le quali si verifica tale comportamento sono dette ferromagnetiche.
Nelle sostanze non ferromagnetiche il valore della permeabilità magnetica differisce di poco rispetto a quella del vuoto, e si dividono in diamagnetiche (in cui la permeabilità relativa è minore di 1) e paramagnetiche (in cui la permeabilità relativa è maggiore di 1). Ciò si differenzia rispetto alla permittività elettrica, che può differire di molto dal valore nel vuoto e cambia sensibilimente a seconda della sostanza, assumendo però sempre valori maggiori rispetto a quello nel vuoto.
La permeabilità magnetica del vuoto è una delle costanti fisiche fondamentali. Il suo valore in unità del SI è:
Spesso la permeabilità si esprime come il prodotto della permeabilità relativa e di quella del vuoto .[2]
Definizione[modifica | modifica wikitesto]
La permeabilità magnetica di un materiale è data dalla relazione costitutiva:
dove è l'induzione magnetica e l'intensità del campo magnetico.[3] La permeabilità magnetica dipende, in generale, dalla posizione all'interno del materiale e dalla direzione del campo magnetico: viene pertanto descritta con un tensore del secondo ordine (matrice 3x3), che nel caso in cui il mezzo sia isotropo e omogeneo si riduce ad uno scalare. Inoltre, la permeabilità dipende anche dalla frequenza del campo, e quindi è una funzione complessa della frequenza. Varia anche in funzione di altri fattori, solitamente trascurabili, come l'umidità e la temperatura.
Polarizzazione magnetica[modifica | modifica wikitesto]

Le proprietà magnetiche di un materiale possono essere descritte e modellizzate a partire dal fatto che una spira percorsa da corrente elettrica si comporta, a grande distanza, come un dipolo magnetico. Sfruttando il modello planetario dell'atomo, ogni elettrone costituisce una microscopica spira percorsa da una corrente (il muoversi dell'elettrone stesso) che in assenza di campi elettromagnetici esterni è orientata casualmente. La presenza di un campo magnetico locale comporta un'orientazione collettiva delle spire. L'effetto di tale polarizzazione può essere descritto riconducendo le correnti microscopiche di magnetizzazione ad una grandezza vettoriale macroscopica, che descriva il comportamento globale del materiale soggetto alla presenza del campo magnetico: il vettore intensità di magnetizzazione, anche detto vettore di polarizzazione magnetica e indicato con , è il momento di dipolo magnetico per unità di volume posseduto dal materiale. Definito come il valore medio del momento magnetico proprio di particelle contenute in un volume infinitesimo , è espresso dalla relazione:[4]
Nel Sistema internazionale di unità di misura il vettore di polarizzazione magnetica si misura in ampere su metro (A/m), e nella definizione il limite vale per un volume che contenga un numero significativo di atomi tale da poterne calcolare una proprietà media.
La polarizzazione della materia costringe a tenere conto delle correnti microscopiche aggiuntive che si formano nel materiale, e la quarta equazione di Maxwell assume la forma:[5]
dove è il vettore campo magnetico nella materia, dato da:[6]
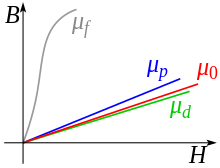
Dal momento che non tutti i materiali hanno una relazione lineare tra e , i materiali magnetici si distinguono in tre categorie:
- I materiali ferromagnetici, come ferro, cobalto e nichel, sono caratterizzati dal fatto che i campi e non sono paralleli, e la permeabilità caratteristica ha un comportamento che segue un certo ciclo isteresi, ovvero dipende dalle precedenti magnetizzazioni e smagnetizzazioni subite da tali materiali. Più precisamente, nelle sostanze ferromagnetiche la permeabilità è funzione del campo magnetico .
- I materiali diamagnetici, caratterizzati da una permeabilità caratteristica costante ma minore dell'unità e indipendente da .
- I materiali paramagnetici, caratterizzati da una permeabilità caratteristica costante e maggiore dell'unità e indipendente da .
Esistono inoltre i materiali giromagnetici, per i quali la permeabilità per campi elettromagnetici oscillanti ha la forma tensoriale:
in cui è la frequenza di oscillazione del campo.
Suscettività magnetica, permittività elettrica e indice di rifrazione[modifica | modifica wikitesto]
La suscettività magnetica e la permeabilità magnetica sono legate dalla seguente relazione:
La velocità della luce in un mezzo è definita a partire dalla permittività elettrica e dalla permeabilità magnetica:
Pertanto, la permittività e l'indice di rifrazione sono legati dalla relazione:[7][8]
Permeabilità complessa[modifica | modifica wikitesto]
In un materiale lineare si verifica che per basse frequenze il campo magnetico e il campo che si forma in seguito alla polarizzazione sono sostanzialmente proporzionali. Ad alte frequenze si verifica che la risposta del materiale non è istantanea, ma al variare di la modifica del valore di avviene dopo un certo piccolo intervallo di tempo.[9] La permeabilità deve esprimere in tal caso uno sfasamento tra e , e pertanto è descritta con un numero complesso. Scrivendo i campi come fasori:
dove è lo sfasamento, si ha:
Utilizzando la formula di Eulero si ottiene la forma rettangolare della permeabilità complessa:
Il rapporto:
quantifica l'assorbimento di energia elettromagnetica da parte del mezzo.
Permeabilità di alcuni materiali[modifica | modifica wikitesto]
| Materiale | Suscettività χm (volumetrica SI) |
Permeabilità μ [H/m] | Permeabilità relativa μ/μ0 | Induzione Magnetica | Frequenza massima |
|---|---|---|---|---|---|
| Metglas | 1.25 | 1000000[10] | 0.5 T | 100 kHz | |
| Nanoperm | 1 × 10−2 | 80000[11][12] | 0.5 T | 10 kHz | |
| Mu-metal | 2.5 × 10−2 | 20000[13] | 0.002 T | ||
| Mu-metal | 50000[14] | ||||
| Permalloy | 8000 | 1.0 × 10−2 | 8000[13] | 0.002 T | |
| Ferrite (manganese, zinco) | > 8.0 × 10−4 | 640 (o maggiore) | 100 kHz ~ 1 MHz | ||
| Acciaio | 8.75 × 10−4 | 100[13] | 0.002 T | ||
| Nichel | 1.25 × 10−4 | 100[13] – 600 | 0.002 T | ||
| Magneti al neodimio | 1.31946891 × 10−6 | 1.05[15] | |||
| Platino | 1.2569701 × 10−6 | 1.000265 | |||
| Alluminio | 2.22 × 10−5[16] | 1.2566650 × 10−6 | 1.000022 | ||
| Legno | 1.00000043[16] | ||||
| Aria | 1.2566375 × 10−6 | 1.00000037[17] | |||
| Calcestruzzo | 1[18] | ||||
| Vuoto | 0 | 4π × 10−7 (μ0) | 1[19] | ||
| Idrogeno | -2.2 × 10−9[16] | 1.2566371 × 10−6 | 1.0000000 | ||
| Teflon | 1.2567 × 10−6[13] | 1.0000 | |||
| Zaffiro | -2.1 × 10−7 | 1.2566368 × 10−6 | 0.99999976 | ||
| Rame | -6.4 × 10−6 o -9.2 × 10−6[16] |
1.2566290 × 10−6 | 0.999994 | ||
| Acqua | -8.0 × 10−6 | 1.2566270 × 10−6 | 0.999992 | ||
| Bismuto | -1.66 × 10−4 | 1.25642846 × 10−6 | 0.999834 | ||
| Grafite Pirolitica | -4.00 x 10- 4 | 0.9996 | |||
| Superconduttore | −1 | 0 | 0 |
Note[modifica | modifica wikitesto]
- ^ (EN) IUPAC Gold Book, "permeability of vacuum"
- ^ (EN) IUPAC Gold Book, "permeability"
- ^ Jackson, Pag. 780.
- ^ Mencuccini, Silvestrini, Pag. 305.
- ^ Mencuccini, Silvestrini, Pag. 309.
- ^ Mencuccini, Silvestrini, Pag. 310.
- ^ Griffiths, section 9.4.1.
- ^ Jackson, Section 5.18A
- ^ M. Getzlaff, Fundamentals of magnetism, Berlin: Springer-Verlag, 2008.
- ^ "Metglas Magnetic Alloy 2714A", ''Metglas'', su metglas.com. URL consultato l'8 novembre 2011 (archiviato dall'url originale il 6 febbraio 2012).
- ^ "Typical material properties of NANOPERM", ''Magnetec'' (PDF) [collegamento interrotto], su magnetec.de. URL consultato l'8 novembre 2011.
- ^ (DE, EN) MAGNETEC (PDF), su mhw-intl.com. URL consultato il 9 dicembre 2022 (archiviato il 9 dicembre 2022).
- ^ a b c d e "Relative Permeability", ''Hyperphysics'', su hyperphysics.phy-astr.gsu.edu. URL consultato l'8 novembre 2011.
- ^ Nickel Alloys-Stainless Steels, Nickel Copper Alloys, Nickel Chromium Alloys, Low Expansion Alloys, su nickel-alloys.net. URL consultato l'8 novembre 2011.
- ^ Juha Pyrhönen, Tapani Jokinen, Valéria Hrabovcová, Design of Rotating Electrical Machines, John Wiley and Sons, 2009, p. 232, ISBN 0-470-69516-1.
- ^ a b c d Richard A. Clarke, Clarke, R. ''Magnetic properties of materials'', surrey.ac.uk, su ee.surrey.ac.uk. URL consultato l'8 novembre 2011 (archiviato dall'url originale il 3 giugno 2012).
- ^ B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, 568 pp., p.16
- ^ NDT.net, Determination of dielectric properties of insitu concrete at radar frequencies, su ndt.net. URL consultato l'8 novembre 2011.
- ^ valore esatto, per definizione
Bibliografia[modifica | modifica wikitesto]
- Corrado Mencuccini, Vittorio Silvestrini, Fisica II, Napoli, Liguori Editore, 2010, ISBN 978-88-207-1633-2.
- (EN) John D Jackson, Classical Electrodynamics, 3rd Edition, Wiley, 1999, ISBN 0-471-30932-X.
- (EN) Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X.
- Jerry D. Wilson, Antony J. Buffa, Fisica 3, Milano, Principato, 2000, ISBN 88-416-5803-7
- Paride Nobel, Fenomeni fisici, Napoli, Editrice Ferraro, 1994 ISBN 88-7271-126-6
- Michelangelo Fazio, SI, MKSA, CGS & Co. dizionario e manuale delle unità di misura, Bologna, Zanichelli Editore, 1995, ISBN 88-08-08962-2.
- (EN) Robert Perry, Dow.W.Green, Perry's Chemical Engineers' Handbook, 8ª ed., McGraw-Hill, 2007, ISBN 0-07-142294-3.
- (EN) IUPAC Quantities, Units and Symbols in Physical Chemistry, Ian Mills, Tomislav Cvitas, Klaus Homann, Nicola Kallay, Kozo Kuchitsu, 1993, 2ª ed., Blackwell Science, ISBN 0-632-03583-8.
Voci correlate[modifica | modifica wikitesto]
- Campo magnetico
- Diamagnetismo
- Dipolo magnetico
- Equazioni di Maxwell
- Ferrimagnetismo
- Ferromagnetismo
- Paramagnetismo
- Permittività elettrica
- Polarizzazione magnetica
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su permeabilità magnetica
Wikimedia Commons contiene immagini o altri file su permeabilità magnetica
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Kaye & Laby Magnetic properties of materials (National Physical Laboratory, Inghilterra)
- (EN) Hyperphysics Magnetic Susceptibilities of Paramagnetic and Diamagnetic Materials at 20 °C (Georgia State University, Stati Uniti)
- (EN, FR) Sito web del BIPM, l'Ufficio internazionale dei pesi e delle misure, su bipm.fr.
- (EN, FR) SI brochure, 8ª Ed. 2006 (PDF, 3,88 MB)
- (EN) Sito dell'istituto nazionale degli Stati Uniti per gli standard e le tecnologie, NIST, su nist.gov.
- (EN) Il Sistema internazionale di unità di misura, pubblicazione speciale 330, NIST 2008 (PDF), su physics.nist.gov.
- (EN) Guida per l'uso del Sistema internazionale di unità di misura, pubblicazione speciale 811, NIST 2008 (PDF), su physics.nist.gov.
| Controllo di autorità | LCCN (EN) sh85079728 · J9U (EN, HE) 987007543559805171 |
|---|





























