Indice di rifrazione
In fisica, l'indice di rifrazione (IOR: Index Of Refraction) di un materiale è una grandezza adimensionale che quantifica la diminuzione della velocità di propagazione della radiazione elettromagnetica quando attraversa un materiale. Si definisce come:
dove è la velocità della luce nel vuoto, mentre è la velocità con cui questa attraversa il materiale in questione. La diminuzione della velocità di propagazione viene accompagnata dalla variazione della sua direzione, secondo il fenomeno della rifrazione.
Si tratta di una grandezza utilizzata in svariati ambiti della scienza, e la sua misura può essere usata per identificare la natura del materiale in cui si propaga la radiazione. Ad esempio, in chimica vengono comunemente effettuate misure dell'indice di rifrazione con lo scopo di trarne indicazioni analitiche. In funzione dei parametri solvente, lunghezza d'onda incidente e temperatura, si effettua la misura del parametro utilizzando un rifrattometro. Questa metodica analitica viene utilizzata in vari campi: in campo medico per analisi del sangue e delle urine, in ambito industriale nell'analisi dei materiali, per determinare la concentrazione zuccherina in succhi di frutta o il grado alcolico di bevande, per certificare il livello qualitativo o evidenziare sofisticazioni di alimenti quali l'olio, il latte e il burro.
Definizione[modifica | modifica wikitesto]
| Materiale | n a λ=589,3 nm |
|---|---|
| elio | 1,000 036 |
| aria in condizioni normali | 1,000 292 6 |
| anidride carbonica | 1,000 45 |
| ghiaccio | 1,31 |
| acqua (20 °C) | 1,333 |
| etanolo | 1,36 |
| glicerina | 1,472 9 |
| sale | 1,516 |
| bromo | 1,661 |
| vetro (tipico) | da 1,5 a 1,9 |
| diamante | 2,419 |
| silicio | 3,4 |
| fosfuro di gallio | 3,5 |
| Olii | |
| Lino | 1,45 |
| D'oliva | 1,467 |
| Mandorle dolci | 1,47 |
| Melaleuca | 1,475 |
| Chiodi di Garofano | 1,535 |
| Gaultheria | 1,536 |
| Miristicina | 1,895 |
La radiazione viaggia alla massima velocità , detta velocità della luce, quando si trova nel vuoto. L'indice di rifrazione è il rapporto tra e la velocità di propagazione della radiazione nel mezzo:
In generale, questo indice non è costante, ma varia in base alla frequenza della radiazione. Infatti i materiali e le radiazioni interagiscono in maniera diversa per frequenze d'onda diverse, mostrando fenomeni di assorbimento anche molto intensi. Pertanto, anche se solitamente viene riportato un numero reale, dal punto di vista matematico si tratta di un numero complesso strettamente legato alla permittività elettrica.
Ad esempio per l'acqua si fornisce normalmente un indice di 1,33, ma se la frequenza dell'onda è attorno ai 2,4 GHz, come nel forno a microonde, per via delle specifiche proprietà delle molecole di acqua allo stato liquido, la parte reale dell'indice vale circa 9.[1]
Si consideri un'onda elettromagnetica monocromatica, che scritta in funzione del campo elettrico ha la forma:
dove è l'ampiezza e è la frequenza angolare dell'onda. Il vettore d'onda è dato da , con la direzione di propagazione e il numero d'onda:
in cui il numero:
è la lunghezza d'onda della radiazione quando si propaga nel vuoto. La lunghezza d'onda nel materiale è data da:
e l'indice di rifrazione (in assenza di assorbimento) è:
dove è la velocità di fase, cioè la velocità alla quale si propagano le creste dell'onda.
Derivazione dalle equazioni di Maxwell[modifica | modifica wikitesto]
Le equazioni di Maxwell in un materiale possono essere scritte come:
assieme alle equazioni costitutive:
che descrivono la reazione nel mezzo alla presenza di un campo elettromagnetico.
Per risolvere queste equazioni è necessario formulare delle ipotesi (che rappresentano inevitabilmente un'approssimazione) sulla dipendenza di ed da e da . Assumendo , un'approssimazione al primo ordine è che la polarizzazione del mezzo sia lineare con il campo elettrico:
dove è la suscettività elettrica. Questa approssimazione è valida a meno che non si considerino campi estremamente intensi, come quelli che si possono ottenere con un laser: quando non è più valida si entra nel regime dell'ottica non lineare. Si assume inoltre che non ci siano cariche libere, ovvero che e :
derivando rispetto al tempo la quarta equazione e facendo il rotore della seconda si ottiene:
Uguagliando allora il rotore della derivata nel tempo di (dalla prima relazione) con la derivata nel tempo del rotore di (primo termine della seconda relazione) si ha:
La prima equazione implica che la divergenza del campo elettrico è nulla. Dall'analisi differenziale è noto che per un generico vettore si ha:
Da queste segue che il rotore del campo elettrico è pari all'opposto del laplaciano del campo stesso:
Ricordandosi che la velocità della luce può essere scritta come:
questa diventa:
ossia l'equazione di un'onda che si propaga, non a velocità ma ad una velocità di fase inferiore pari a:
Il fattore è l'indice di rifrazione, e può essere riscritto in funzione della costante dielettrica e della permeabilità magnetica del mezzo come:
Nel caso in cui sia che siano negativi la soluzione corretta delle equazioni di Maxwell impone che si debba scegliere come indice di rifrazione la radice negativa, e quindi . Questa condizione non viene mai raggiunta nei materiali reali ma è stata dimostrata la possibilità di usare dei metamateriali per ottenerla.
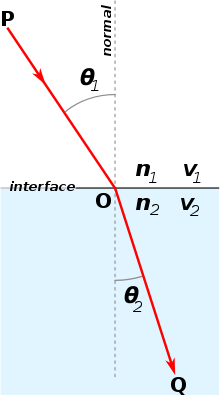
Legge di Snell[modifica | modifica wikitesto]
La legge di Snell descrive quanto la direzione di propagazione della luce è deviata nel passare da un mezzo ad un altro. Essa afferma che se il raggio proviene da una regione con indice di rifrazione ed entra in un mezzo ad indice , gli angoli di incidenza e di rifrazione sono legati dall'espressione:
dove e sono le velocità nei mezzi, e la velocità della radiazione deve cambiare da a . Se non vi è nessun angolo che soddisfa la relazione, ovvero:
la luce non viene trasmessa nel secondo mezzo e si verifica il fenomeno di riflessione interna totale.
A partire dalle equazioni di Maxwell è possibile dimostrare, sfruttando il fatto che il campo elettrostatico è conservativo, che passando da un mezzo ad un altro la componente del campo elettrico tangente all'interfaccia è continua. Questo si relaziona al fatto che, dal momento che l'intensità del vettore d'onda è proporzionale all'energia del fotone incidente, la sua componente trasversale si deve conservare. Dato che la componente trasversale del vettore d'onda resta uguale, si ha che e quindi:
da cui .
Riflettanza[modifica | modifica wikitesto]
Quando un'onda elettromagnetica incide sul materiale, parte di essa viene riflessa. La quantità di luce che viene riflessa dipende dalla riflettanza della superficie. Tale grandezza può essere calcolata a partire dall'indice di rifrazione e dall'angolo di incidenza per mezzo dell'equazione di Fresnel, secondo la quale la componente normale della riflessione viene ridotta di:
Per il vetro immerso in aria e , che significa che il 4% della potenza viene riflessa.[2]
Vi è un angolo , detto angolo di Brewster, per cui la radiazione polarizzata lungo il piano di incidenza viene totalmente trasmessa:
e non vi è dunque riflessione.
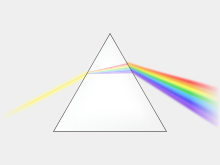
Dispersione[modifica | modifica wikitesto]
In tutti i sistemi reali l'indice di rifrazione varia con la frequenza dell'onda incidente, e per la legge di Snell a frequenze diverse corrispondono angoli di rifrazione diversi. Un esempio ben noto di questo fenomeno è il fatto che la luce bianca (contenente tutte le componenti spettrali) viene scomposta da un prisma.
Quando un materiale presenta assorbimento non è più possibile descrivere l'indice di rifrazione tramite un numero reale ma bisogna definire un indice di rifrazione complesso:
dove definisce la velocità di fase con cui si propaga l'onda e è proporzionale al coefficiente di assorbimento del sistema. L'assorbimento dell'energia della radiazione da parte del materiale è strettamente legato al fenomeno della dispersione, e le quantità e sono legate dalla relazione di Kramers-Kronig.
Per mostrare che quantifica l'assorbimento dell'energia del campo è sufficiente inserire nell'espressione del campo elettrico in un'onda piana che si propaga in direzione z:
Considerando il vettore d'onda come numero complesso , la cui parte reale è , si ha:
Si nota che fornisce un decadimento esponenziale, come previsto dalla legge di Lambert-Beer. Dato che l'intensità dell'onda è proporzionale al quadrato dell'intensità del campo elettrico, il coefficiente di assorbimento diventa .
In alcune condizioni particolari (ad esempio vicino a delle risonanze dell'assorbimento) è possibile che sia minore di 1. In questi casi la velocità di fase può essere superiore alla velocità della luce. Questo però non viola la relatività ristretta perché la velocità del segnale è la velocità di gruppo la quale rimane sempre inferiore a .
Assorbimento[modifica | modifica wikitesto]
L'assorbimento di un materiale è la sua capacità di assorbire l'energia associata alla radiazione elettromagnetica che si propaga all'interno di esso.[3] Si tratta dell'energia dei fotoni che viene ceduta agli elettroni, atomi e molecole del materiale: l'energia del campo elettromagnetico si trasforma in questo modo in energia interna del materiale, come ad esempio la sua energia termica. Solitamente l'intensità dell'onda elettromagnetica non influisce sull'assorbimento (in caso contrario si parla di assorbimento non lineare), e la sua riduzione è anche detta attenuazione.
L'assorbimento dipende sia dalla natura del materiale, sia dalla frequenza della radiazione, e può essere quantificato attraverso la permittività elettrica: si tratta di una funzione complessa della frequenza dell'onda, attraverso la quale è possibile trattare la propagazione del campo elettromagnetico in mezzi dissipativi. Normalmente il valore della permittività elettrica viene scritto come il prodotto della permittività relativa e della permettività del vuoto , detta anche costante dielettrica del vuoto. Poiché varia a seconda della direzione del campo elettrico rispetto al mezzo, essa è rappresentata attraverso un tensore, e solo nel caso di un dielettrico perfetto tutte le componenti del tensore hanno lo stesso valore, chiamato impropriamente costante dielettrica.
La permittività e l'indice di rifrazione sono legati dalla relazione:[4][5]
dove è la permeabilità magnetica relativa e la permittività elettrica relativa, un numero complesso:
In un mezzo con (approssimazione valida per la maggior parte dei materiali), la permittività elettrica è dunque il quadrato dell'indice di rifrazione complesso. Valgono le seguenti relazioni:[6]
Quando si analizza la permittività dal punto di vista della frequenza del campo si nota che essa può presentare un comportamento anomalo in corrispondenza di certe lunghezze d'onda. Infatti, la parte immaginaria della permittività elettrica segue un andamento risonante in corrispondenza dei suoi poli, dove presenta uno o più picchi. In corrispondenza di questi picchi l'assorbimento da parte del materiale dell'energia posseduta dal campo è massimo.
La birifrangenza[modifica | modifica wikitesto]
Nei materiali anisotropi la polarizzazione non dipende solo dall'intensità del campo elettrico ma anche dalla sua polarizzazione, ovvero la costante dielettrica non è uguale sui tre assi del sistema di riferimento. Di conseguenza la costante dielettrica non può più essere descritta tramite uno scalare ma deve essere rappresentato tramite una matrice (o, più formalmente, tramite un tensore). In questo caso si ha il fenomeno detto di birifrangenza dove fasci di luce con polarizzazione diversa ed incidenti ad angoli diversi vedono un indice di rifrazione diverso e quindi vengono rifratti in direzioni diverse. Storicamente questo fenomeno è stato osservato per la prima volta nella calcite.
La birifrangenza è molto sfruttata sia nell'ottica non lineare che per la realizzazione di dispositivi elettro-ottici, per esempio lamine che funzionano da ritardatore di fase (lamine a mezz'onda o quarto d'onda), o dispositivi per la generazione di seconda armonica in un laser.
Note[modifica | modifica wikitesto]
- ^ Microwaves in other media, domanda su Physics Stack Exchange
- ^ Jim Swenson, Incorporates Public Domain material from the U.S. Department of Energy, Refractive Index of Minerals, su newton.dep.anl.gov, Newton BBS, Argonne National Laboratory, US DOE, November 10, 2009. URL consultato il 28 luglio 2010 (archiviato dall'url originale il 28 maggio 2010).
- ^ William West, Absorption of electromagnetic radiation, su AccessScience, McGraw-Hill. URL consultato l'8 aprile 2013.
- ^ Griffiths, section 9.4.1.
- ^ Jackson, Section 5.18A
- ^ Frederick Wooten, Optical Properties of Solids, New York City, Academic Press, 1972, p. 49, ISBN 0-12-763450-9.
Bibliografia[modifica | modifica wikitesto]
- Richard Feynman, La fisica di Feynman, Bologna, Zanichelli, 2001.:
- Vol I, cap. 27: Ottica geometrica
- Vol I, cap. 31: L'origine dell'indice di rifrazione
- Corrado Mencuccini, Vittorio Silvestrini, Fisica II, Napoli, Liguori Editore, 2010, ISBN 978-88-207-1633-2.
- (EN) John D Jackson, Classical Electrodynamics, 3rd Edition, Wiley, 1999, ISBN 0-471-30932-X.
- (EN) Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X.
- (EN) Alfred Barnard Basset A treatise on Physical Optics (Cambridge: Deighton, Bell, 1892) (storico, descrizione delle vecchie teorie dell'indice di rifrazione e della teoria elettromagnetica di Maxwell).
- (EN) Paul Drude The theory of Optics pp. 268–396 (New York: Longmans, Green, and Co. 1902).
Indice di rifrazione di sostanze varie[modifica | modifica wikitesto]
- (FR) Henry Dufet Recueil de données numériques: optique[collegamento interrotto] (Parigi: Gauthier-Villars et fils, 1898-1900)
- (DE) Hans Landolt e Richard Börnstein Landolt-Börnstein physikalisch-chemische tabellen (Berlino, Springer, 1912) (pp. 967–1046)
- (EN) John Naish Goldsmith e R. Kanthack Tables of refractive indices v. 2. Oils, fats and waxes (London: A. Hilger, 1918)
- (EN) Frederick Eugene Fowle Smithsonian physical tables (Washington, The Smithsonian Institution, 1920) (pp. 277–296)
- (EN) George William Clarkson Kaye e Thomas Howell Laby Tables of physical and chemical constants and some mathematical functions (London: Longman Greens & co. 1921) (pp. 75–78)
- (EN) Richard Glazebrook A Dictionary of Applied Physics vol. 4: Light, Sound, Radiology (1923) (Voci Glass p. 96 e Optical Glass pp. 315–325)
- (EN) Gustav Egloff Physical Constants Of Hydrocarbons Vol I: Paraffins, Olefins, acetylenes and other aliphatic hydrocabons (New York: Reinhold Publishing Corporation, 1939)
- (EN) Gustav Egloff Physical Constants Of Hydrocarbons Vol II: Cyclenes, Cyclynics (New York: Reinhold Publishing Corporation, 1940)
- (EN) Gustav Egloff Vol. III: Mononuclear Aromatic Hydrocarbons (New York: Reinhold Publishing Corporation, 1946)
- (EN) Gustav Egloff Vol. IV: Polynuclear Aromatic Hydrocarbons (New York: Reinhold Publishing Corporation, 1947)
Voci correlate[modifica | modifica wikitesto]
- Onda (fisica)
- Campo elettromagnetico
- Legge di Snell
- Leggi di Fresnel
- Radiazione elettromagnetica
- Velocità della luce
- Luce
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sull'indice di rifrazione
Wikimedia Commons contiene immagini o altri file sull'indice di rifrazione
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) refractive index / negative refractive index, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) IUPAC Gold Book, "refractive index", su goldbook.iupac.org.
- Indici di rifrazione (rispetto alla luce gialla del sodio), su itchiavari.org.
- (EN) l'indice di rifrazione su World of Physics, su scienceworld.wolfram.com.
| Controllo di autorità | Thesaurus BNCF 34514 · LCCN (EN) sh85112261 · GND (DE) 4146524-6 · J9U (EN, HE) 987007529453605171 |
|---|












































































