Leggi di Fresnel
Le leggi di Fresnel, dedotte da Augustin-Jean Fresnel (pronuncia IPA: [freˈnɛl]), descrivono insieme alle leggi di Snell il comportamento della luce quando attraversa una superficie che divide due mezzi con diversi indici di rifrazione.
In particolare grazie alle leggi di Fresnel è possibile calcolare come l'intensità di un raggio luminoso incidente su una superficie viene ripartita tra il raggio riflesso e il raggio rifratto.
La riflessione della luce espressa dalle leggi è detta riflessione di Fresnel.
Riflessione e rifrazione[modifica | modifica wikitesto]
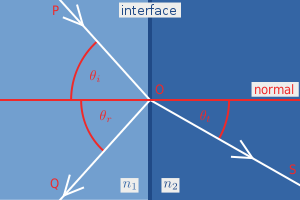
Quando la luce si sposta da un mezzo con un dato indice di rifrazione verso un secondo mezzo con indice , possono verificarsi sia la riflessione che la rifrazione dell'onda luminosa stessa.
Nella figura a destra, un raggio di luce incidente PO colpisce sul punto O l'interfaccia tra due mezzi con indici di rifrazione e . Parte del raggio viene riflessa come raggio OQ e parte viene rifratta seguendo la traiettoria OS. Gli angoli che l'onda incidente, riflessa e rifratta formano con la normale all'interfaccia sono e , rispettivamente. Le relazioni tra questi angoli sono date dalla legge della riflessione e dalla legge di Snell.
Coefficiente di riflessione[modifica | modifica wikitesto]
Il coefficiente di riflessione o riflettività spettrale è il rapporto tra le intensità della radiazione riflessa () e della radiazione incidente ():
Il suo valore dipende dalla polarizzazione del raggio incidente, che viene separato in due componenti con polarizzazione perpendicolare tra loro:
Polarizzazione S (Campo elettrico)[modifica | modifica wikitesto]
Una componente è polarizzata con il campo elettrico dell'onda perpendicolare al piano di propagazione (dato dalla direzione di propagazione dell'onda incidente e dalla normale all'interfaccia) — situazione detta polarizzazione S (da senkrecht, parola tedesca che significa perpendicolare) o TE (dalla lingua inglese: transverse electric) — il suo coefficiente di riflessione è dato da:
- È importante ricordare che tale formula per il coefficiente di riflessione è valida solo nel caso in cui si considerano entrambi i mezzi in cui si propaga l'onda non magnetici, cioè caratterizzati da permeabilità relativa .
Polarizzazione P (campo magnetico)[modifica | modifica wikitesto]
L'altra componente ha invece il campo magnetico che oscilla perpendicolarmente al piano di propagazione (di conseguenza, il campo elettrico è parallelo a tale piano) — situazione chiamata polarizzazione P o TM (dall'inglese transverse magnetic) — il coefficiente è pari a:
- È importante ricordare che tale formula per il coefficiente di riflessione è valida solo nel caso in cui si considerano entrambi i mezzi in cui si propaga l'onda non magnetici, cioè caratterizzati da permeabilità relativa .
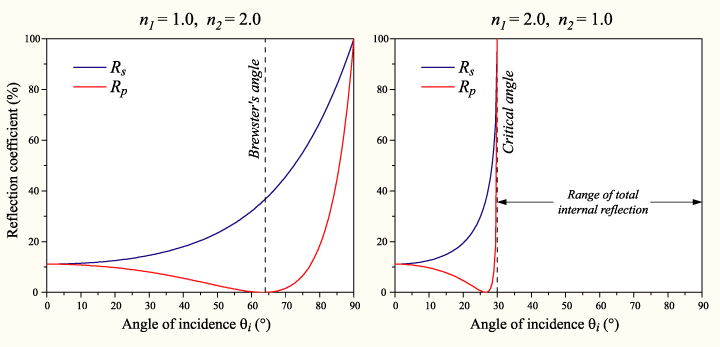
Angolo di Brewster e angolo critico[modifica | modifica wikitesto]
A un particolare angolo che dipende da e , il valore di per la polarizzazione P può annullarsi: quella componente è totalmente rifratta, e il raggio riflesso è polarizzato S, con direzione quindi perpendicolare al piano di incidenza. Questo angolo è chiamato angolo di Brewster, e il fenomeno prende nome di rifrazione totale.
Il valore di questo angolo può essere calcolato con:
che nel caso del passaggio da aria o vuoto a vetro risulta circa 56°.
Se (ad esempio quando si passa da un materiale più denso ad uno meno denso), sopra un angolo di incidenza noto come angolo critico, tutta la luce viene riflessa e . Questo fenomeno è noto come riflessione interna totale. Per il vetro nell'aria, l'angolo critico è circa pari a 41°.
Coefficiente di trasmissione[modifica | modifica wikitesto]
Il coefficiente di trasmissione è il rapporto tra le intensità della radiazione trasmessa () e della radiazione incidente ():
Dato che il raggio incidente si divide in raggio riflesso e raggio rifratto, vale l'equazione:
da cui:
Quindi il coefficiente di trasmissione può essere calcolato da quello di riflessione, per entrambe le polarizzazioni:
Equazioni semplificate[modifica | modifica wikitesto]
Quando la luce è a un'incidenza quasi normale rispetto all'interfaccia (), i coefficienti di trasmissione e di riflessione si semplificano:
Per il vetro comune, il coefficiente di riflessione è circa del 4% (circa il 4% di un'onda incidente viene riflessa). È da notare che la riflessione per una finestra avviene da entrambe le superfici; il coefficiente di riflessione combinato è in questo caso , quando si trascura l'interferenza.
In realtà, quando la luce compie riflessioni multiple tra due superfici parallele, i raggi interferiscono l'uno con l'altro e le superfici agiscono da interferometro di Fabry-Pérot. Questo effetto è responsabile del colore che si deve nei film sull'acqua, ed è utilizzato nell'ottica per costruire copertura antiriflesso che abbassano la riflessione.
Validità delle leggi di Fresnel[modifica | modifica wikitesto]
Gli indici di rifrazione variano a seconda della lunghezza d'onda, perciò tutto quanto detto finora deve essere applicato tenendo conto di questo fatto.
Bisogna notare che la discussione svolta qui sopra suppone che la permeabilità magnetica sia uguale alla permeabilità del vuoto in entrambi i mezzi. Questo è vero nella maggior parte dei mezzi dielettrici, ma non per altri tipi di materiali. Le equazioni complete di Fresnel risultano quindi più complicate.
Inoltre, perché queste leggi siano applicabili si suppone che la magnetizzazione , il campo elettrico tangenziale alla superficie e il campo magnetico normale alla superficie siano uniformi.
Voci correlate[modifica | modifica wikitesto]
- Integrale di Fresnel
- Lente di Fresnel
- Numero di Fresnel
- Riflessione interna totale
- Rifrazione totale
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su leggi di Fresnel
Wikimedia Commons contiene immagini o altri file su leggi di Fresnel
Collegamenti esterni[modifica | modifica wikitesto]
- Equazioni di Fresnel – Mathworld
- FreeSnell – Software libero per il calcolo delle proprietà ottiche dei materiali.







![{\displaystyle R_{s}=\left[{\frac {\sin(\theta _{t}-\theta _{i})}{\sin(\theta _{i}+\theta _{t})}}\right]^{2}=\left[{\frac {n_{1}\cos(\theta _{i})-n_{2}\cos(\theta _{t})}{n_{1}\cos(\theta _{i})+n_{2}\cos(\theta _{t})}}\right]^{2}=\left[{\frac {n_{1}\cos {\theta _{i}}-n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}{\theta _{i}}}}}{n_{1}\cos {\theta _{i}}+n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}{\theta _{i}}}}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e17fd6cc96c3fdecda49ebe794afeab4a011c894)


![{\displaystyle R_{p}=\left[{\frac {\tan(\theta _{i}-\theta _{t})}{\tan(\theta _{i}+\theta _{t})}}\right]^{2}=\left[{\frac {n_{1}\cos(\theta _{t})-n_{2}\cos(\theta _{i})}{n_{1}\cos(\theta _{t})+n_{2}\cos(\theta _{i})}}\right]^{2}=\left[{\frac {n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}{\theta _{i}}}}-n_{2}\cos(\theta _{i})}{n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}{\theta _{i}}}}+n_{2}\cos(\theta _{i})}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc2442179b54311a0cdd0b697d596132420b0f3)