Effetto fotoelettrico
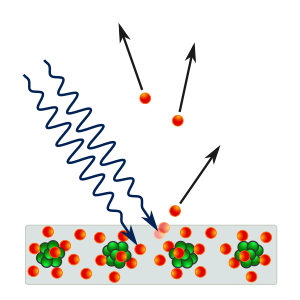
In fisica l'effetto fotoelettrico è un fenomeno quantistico consistente nell'emissione di elettroni da una superficie metallica quando viene colpita da una radiazione elettromagnetica di frequenza non inferiore a un certo valore soglia caratteristico di ogni metallo (soglia fotoelettrica).[1]
Storia[modifica | modifica wikitesto]

La scoperta dell'effetto fotoelettrico va fatta risalire alla seconda metà del XIX secolo e ai tentativi di spiegare la conduzione nei liquidi e nei gas. Nel 1887, Hertz,[2] riprendendo e sviluppando gli studi di Schuster sulla scarica dei conduttori elettrizzati stimolata da una scintilla elettrica nelle vicinanze, si accorse che tale fenomeno è più intenso se gli elettrodi vengono illuminati con luce ultravioletta. Nello stesso anno, Wiedemann e Ebert stabilirono che la sede dell'azione di scarica è l'elettrodo negativo e Hallwachs trovò che la dispersione delle cariche elettriche negative è accelerata se i conduttori vengono illuminati con luce ultravioletta.
Nei primi mesi del 1888, il fisico italiano Augusto Righi, nel tentativo di capire i fenomeni osservati, scoprì un fatto nuovo: una lastra metallica conduttrice investita da una radiazione UV si carica positivamente. Righi introdusse, per primo, il termine "fotoelettrico" per descrivere il fenomeno. Hallwachs, che aveva sospettato ma non accertato il fenomeno qualche mese prima di Righi, dopo qualche mese, dimostrava, indipendentemente dall'italiano, che non si trattava di trasporto, ma di vera e propria produzione di elettricità.
Sulla priorità della scoperta tra i due scienziati si accese una disputa, riportata sulle pagine del Nuovo Cimento. La comunità scientifica tagliò corto e risolse la controversia chiamando il fenomeno effetto Hertz-Hallwachs. Fu poi Einstein, nel 1905, a darne l'interpretazione corretta, intuendo che l'estrazione degli elettroni dal metallo si spiegava molto più coerentemente ipotizzando che la radiazione elettromagnetica fosse costituita da pacchetti di energia o quanti, poi denominati fotoni.
L'ipotesi quantistica di Einstein non fu accettata per diversi anni da una parte importante della comunità scientifica, tra cui Hendrik Lorentz, Max Planck e Robert Millikan (vincitori del Premio Nobel per la fisica, rispettivamente, nel 1902, 1918 e 1923), secondo i quali la reale esistenza dei fotoni era un'ipotesi inaccettabile, considerato che nei fenomeni di interferenza le radiazioni elettromagnetiche si comportano come onde.[3] L'iniziale scetticismo di questi grandi scienziati dell'epoca non deve sorprendere dato che perfino Max Planck, che per primo ipotizzò l'esistenza dei quanti (anche se con riferimento agli atomi, che emettono e assorbono "pacchetti di energia"), ritenne, per diversi anni, che i quanti fossero un semplice artificio matematico e non un reale fenomeno fisico.[4] Ma, successivamente, lo stesso Robert Millikan dimostrò sperimentalmente l'ipotesi di Einstein sull'energia del fotone, e quindi dell'elettrone emesso, che dipende soltanto dalla frequenza della radiazione,[5] e nel 1916 effettuò uno studio sugli elettroni emessi dal sodio che contraddiceva la classica teoria ondulatoria di Maxwell.[6]
L'aspetto corpuscolare della luce fu confermato definitivamente dagli studi sperimentali di Arthur Holly Compton. Infatti il fisico statunitense nel 1921 osservò che, negli urti con gli elettroni, i fotoni si comportano come particelle materiali aventi energia e quantità di moto che si conservano;[7] nel 1923, pubblicò i risultati dei suoi esperimenti (effetto Compton) che confermavano in modo indiscutibile l'ipotesi di Einstein: la radiazione elettromagnetica è costituita da quanti (fotoni) che interagendo con gli elettroni si comportano come singole particelle.[8] Per la scoperta dell'effetto omonimo, Compton ricevette il premio Nobel nel 1927.
Per i suoi studi sull'effetto fotoelettrico e la conseguente scoperta dei quanti di luce, Einstein ricevette il Premio Nobel per la fisica nel 1921.[9]
Descrizione[modifica | modifica wikitesto]
L'esperimento di Lenard[modifica | modifica wikitesto]

L'effetto fotoelettrico fu rivelato da Hertz nel 1887 nell'esperimento ideato per generare e rivelare le onde elettromagnetiche;[2] in quell'esperimento, Hertz usò uno spinterometro in un circuito accordato per generare onde e un altro circuito simile per rivelarle. Nel 1902 Lenard studiò tale effetto, trovando che la luce incidente su una superficie metallica provoca l'emissione di elettroni, la cui energia non dipende dall'intensità della luce, ma dal suo colore, cioè dalla frequenza.[10]
Quando la luce colpisce una superficie metallica pulita (il catodo C) vengono emessi elettroni. Se alcuni di questi colpiscono l'anodo A, si misura una corrente nel circuito esterno. Il numero di elettroni emessi che raggiungono l'anodo può essere aumentato o diminuito rendendo l'anodo positivo o negativo rispetto al catodo.
Detta V la differenza di potenziale tra A e C, si può vedere che solo da un certo potenziale in poi (detto potenziale d'arresto) la corrente inizia a circolare, aumentando fino a raggiungere un valore massimo, che rimane costante. Questo massimo valore è, come scoprì Lenard, direttamente proporzionale all'intensità della luce incidente. Il potenziale d'arresto è legato all'energia cinetica massima degli elettroni emessi dalla relazione
dove è la massa dell'elettrone, la sua velocità, la sua carica.
Ora, la relazione che lega le due grandezze è proprio quella indicata perché se è negativo, gli elettroni vengono respinti dall'anodo, tranne se l'energia cinetica consente loro, comunque, di arrivare su quest'ultimo. D'altra parte si notò che il potenziale d'arresto non dipendeva dall'intensità della luce incidente, sorprendendo lo sperimentatore, che si aspettava il contrario. Infatti, classicamente, il campo elettrico portato dalla radiazione avrebbe dovuto mettere in vibrazione gli elettroni dello strato superficiale fino a strapparli al metallo. Usciti, la loro energia cinetica sarebbe dovuta essere proporzionale all'intensità della luce incidente e non alla sua frequenza, come invece sembrava risultare sperimentalmente.
Quanto di luce[modifica | modifica wikitesto]
Come comprese Einstein, riprendendo la teoria di Planck, l'effetto fotoelettrico evidenzia la natura quantistica della luce. Nella radiazione elettromagnetica, l'energia non è distribuita in modo uniforme sull'intero fronte dell'onda ma è concentrata in singoli quanti (pacchetti discreti) di energia, i fotoni. Un solo fotone per volta, e non l'intera onda nel suo complesso, interagisce singolarmente con un elettrone, al quale cede la sua energia. Affinché ciò si verifichi è necessario che il singolo fotone abbia un'energia sufficiente a rompere il legame elettrico che tiene legato l'elettrone all'atomo. Questa "soglia minima" di energia del fotone si determina in base alla relazione di Planck
- ,
dove è la costante di Planck, e sono rispettivamente la frequenza e la lunghezza d'onda del fotone, è la velocità della luce (ricordando la relazione ).
In altri termini, l'elettrone può uscire dal metallo solo se l'energia del fotone è almeno uguale al “lavoro di estrazione” (). Esiste, pertanto, una “soglia minima” di estrazione per ogni metallo, che fa riferimento o alla lunghezza d'onda o alla frequenza del fotone incidente e, quindi, alla sua energia , la quale coincide con il “lavoro di estrazione” .
Il valore di soglia varia in base al tipo di materiale considerato (in genere metalli) e dipende, pertanto, dalle sue caratteristiche atomiche; anche il grado di purezza del metallo influisce sul valore di soglia (per tale motivo i testi o i siti specializzati riportano spesso valori di soglia differenti per lo stesso metallo).
Nella tabella che segue sono riportati i valori di soglia di alcuni metalli. Il dato iniziale noto è quello del lavoro di estrazione in eV (col. 2)[11], che equivale al valore di soglia del fotone (in eV) incidente sul metallo considerato; i valori di soglia riportati nelle colonne 3, 4 e 5 sono stati ricavati dalle rispettive formule.
VALORI DI SOGLIA PER L'EMISSIONE DI ELETTRONI DA UN METALLO
| (1) Metallo | (2) E. fotoni (eV) | (3) E. fotoni (J) | (4) frequenza (f) = E(J)/h | (5) lungh. d'onda (λ) = c/f | (6) Rad. E.M. |
|---|---|---|---|---|---|
| Potassio (K) | 2,25 eV | 3,60 x 10−19J | 5,43 x 1014Hz | 552 x 10−9m = 552 nm | luce verde |
| Sodio (Na) | 2,28 eV | 3,65 x 10−19J | 5,51 x 1014Hz | 544 x 10−9m = 544 nm | luce verde |
| Calcio (Ca) | 3,20 eV | 5,13 x 10−19J | 7,74 x 1014Hz | 388 x 10−9m = 388 nm | luce viola |
| Torio (Th) | 3,47 eV | 5,56 x 10−19J | 8,39 x 1014Hz | 357 x 10−9m = 357 nm | raggi u.v. |
| Zinco (Zn) | 4,27 eV | 6,84 x 10−19J | 1,03 x 1015Hz | 291 x 10−9m = 291 nm | raggi u.v. |
| Rame (Cu) | 4,48 eV | 7,18 x 10−19J | 1,08 x 1015Hz | 278 x 10−9m = 278 nm | raggi u.v. |
| Ferro (Fe) | 4,63 eV | 7,42 x 10−19J | 1,12 x 1015Hz | 268 x 10−9m = 268 nm | raggi u.v. |
| Argento (Ag) | 4,70 eV | 7,53 x 10−19J | 1,14 x 1015Hz | 263 x 10−9m = 263 nm | raggi u.v. |
| Nichel (Ni) | 4,91 eV | 7,86 x 10−19J | 1,19 x 1015Hz | 252 x 10−9m = 252 nm | raggi u.v. |
Si precisa che:
- l'energia in eV (col. 2) e l'energia in Joule (col. 3) sono legate dalle relazione per la quale
- l'energia dei fotoni (in ) è data anche dalla legge di Planck: , da cui si ricava la frequenza dei fotoni (col. 4): , dove è la costante di Planck e la frequenza si esprime in Hertz.
- dalla relazione consegue che (col. 5). Da notare che viene espressa generalmente in nanometri, ma nei calcoli va espressa in metri.
Spesso il parametro di soglia iniziale noto è:
- la lunghezza d'onda (in nm); in tal caso occorre determinare anzitutto e successivamente l'energia utilizzando la legge di Planck.
- l'energia dei fotoni incidenti in Joule (uguale a ); in tal caso occorre determinare anzitutto la frequenza , poi (uguale a ) e infine l'energia dei fotoni in eV.
Con l'aumentare dell'energia dei fotoni incidenti (ossia quando aumenta oppure quando diminuisce ) aumenta anche l'energia cinetica degli elettroni estratti.
Va in proposito sottolineato che aumentando l'intensità della radiazione elettromagnetica (ossia il numero di fotoni al secondo, di pari energia, che colpiscono l'unità di superficie) aumenta il numero degli elettroni estratti ma non la loro energia cinetica, la quale dipende esclusivamente dall'energia dei fotoni incidenti. Questa è una conseguenza della teoria quantistica di Einstein, in base alla quale ogni fotone incidente interagisce soltanto con un singolo elettrone. Infatti secondo la teoria ondulatoria classica di Maxwell l'estrazione di elettroni dal metallo dipende dall'intensità dell'irradiamento per unità di superficie (che deve raggiungere un valore sufficiente) e prescinde, quindi, dalla frequenza della radiazione incidente (ipotesi, questa, smentita dalle evidenze sperimentali).
L'effetto fotoelettrico, oggetto di studi da parte di molti fisici, è stato fondamentale per comprendere la natura quantistica della luce.
Un caso particolare di effetto fotoelettrico è l'effetto fotovoltaico.
Emissione di raggi catodici tramite esposizione di corpi solidi[modifica | modifica wikitesto]
Einstein, nel lavoro del 1905 che gli fruttò il Premio Nobel per la fisica nel 1921, fornisce una spiegazione dei fatti sperimentali partendo dal principio che la radiazione incidente possiede energia quantizzata. Infatti i fotoni che arrivano sul metallo cedono energia agli elettroni dello strato superficiale del solido; gli elettroni acquisiscono così l'energia necessaria per rompere il legame: in questo senso l'ipotesi più semplice è che il fotone ceda all'elettrone tutta l'energia in suo possesso. A questo punto l'elettrone spenderà parte dell'energia per rompere il legame e parte incrementerà la sua energia cinetica che gli permetterà di arrivare in superficie e abbandonare il solido: da qui si può capire che saranno gli elettroni eccitati più vicini alla superficie ad avere la massima velocità normale alla stessa. Per questi, posto il lavoro (che varia da sostanza a sostanza) utile all'elettrone per uscire, si avrà che l'energia cinetica è pari a:
A questo punto detta la carica dell'elettrone e il potenziale positivo del corpo e tale da impedire perdita di elettricità allo stesso (il potenziale di arresto), si può scrivere:
oppure, con i simboli consueti
che diventa
dove è la carica di un grammo-equivalente di uno ione monovalente e il potenziale di questa quantità.
Se si pone allora rappresenterà il potenziale in volt del corpo in caso di irradiazione nel vuoto.
Ora, ponendo e (limite dello spettro solare dalla parte ultravioletta), , si ottiene : il risultato trovato è così in accordo, per quanto riguarda gli ordini di grandezza, con quanto trovato da Lenard.
Si può concludere che:
- l'energia degli elettroni uscenti sarà indipendente dall'intensità della luce emettente e anzi dipenderà dalla sua frequenza.
- sarà il numero di elettroni uscenti a dipendere dall'intensità della radiazione.
I risultati matematici cambiano se si rifiuta l'ipotesi di partenza (energia trasmessa totalmente)
che diventa:
per la fotoluminescenza, che è il processo inverso.
Se poi la formula è corretta, riportata sugli assi cartesiani risulterà una retta con pendenza indipendente dalla sostanza. Nel 1916 Millikan eseguì la verifica sperimentale di tale fatto, misurando il potenziale d'arresto e trovando che questo è una retta di con pendenza , come previsto.[12][13]
Applicazioni[modifica | modifica wikitesto]
Le normali cellule fotelettriche dei cancelli automatici funzionano basandosi sull'effetto fotoelettrico: una sorgente elettromagnetica di una cellula sorgente irradia elettromagneticamente a distanza una cellula ricevente che funge da ricevitore trasformandosi in interruttore per il sistema elettromeccanico.[14]
Le celle dei pannelli fotovoltaici producono energia elettrica sfruttando l'effetto fotovoltaico, basato sull'effetto fotoelettrico.[15]
Note[modifica | modifica wikitesto]
- ^ https://www.treccani.it/enciclopedia/effetto-fotoelettrico_%28Enciclopedia-della-Scienza-e-della-Tecnica%29/#:~:text=Fenomeno%20quantistico%20nel%20quale%20si,luce%20incidente%20su%20di%20essa
- ^ a b Heinrich Hertz, Ueber den Einfluss des ultravioletten Lichtes auf die electrische Entladung, in Annalen der Physik, vol. 267, n. 8, 1887, pp. 983–1000, Bibcode:1887AnP...267..983H, DOI:10.1002/andp.18872670827.
- ^ "La fisica di Amaldi", vol. 3, Elettromagnetismo, fisica atomica e subatomica, ed. Zanichelli, 2012, cap. 13 (la teoria quantistica) pag. 416.
- ^ "La fisica di Amaldi", vol. 3, cit., pag. 408.
- ^ "Fotoni pesanti" di Murphy Frederick V. e Yount David E., "Le Scienze" n. 38, ott. 1971, pag. 66.
- ^ " La Fisica di Amaldi ", vol. 3, cit., pag.411.
- ^ “Fotoni pesanti”, "Le Scienze" n. 38/1971 cit.
- ^ "La fisica di Amaldi", vol. 3, cit., pagg. 416 - 417.
- ^ The Nobel Prize in Physics 1921
- ^ P. Lenard, Ueber die lichtelektrische Wirkung, in Annalen der Physik, vol. 313, n. 5, 1902, pp. 149–198, Bibcode:1902AnP...313..149L, DOI:10.1002/andp.19023130510.
- ^ I valori di col. 2 (lavoro di estrazione in eV = energia dei fotoni in eV) sono stati rilevati da: " La fisica di Amaldi ", vol. 3, elettromagnetismo, fisica atomica e subatomica, ed. Zanichelli, 2012, pag.204.
- ^ R. Millikan, A Direct Determination of "h.", in Physical Review, vol. 4, 1914, pp. 73–75, Bibcode:1914PhRv....4R..73M, DOI:10.1103/PhysRev.4.73.2.
- ^ R. Millikan, A Direct Photoelectric Determination of Planck's "h" (PDF), in Physical Review, vol. 7, n. 3, 1916, pp. 355–388, Bibcode:1916PhRv....7..355M, DOI:10.1103/PhysRev.7.355. URL consultato il 13 marzo 2012 (archiviato dall'url originale il 21 novembre 2014).
- ^ fotocellula in "Enciclopedia dei ragazzi", su treccani.it. URL consultato il 4 gennaio 2022.
- ^ Giacomo Torzo, Studio sperimentale di celle fotovoltaiche (PDF), Università degli studi di Udine.
Bibliografia[modifica | modifica wikitesto]
- Albert Einstein, Emissione e trasformazione della luce, da un punto di vista euristico, tratto da Teoria dei quanti di Luce, Edizioni Newton Compton
- Paul A.Tipler, Invito alla fisica, Edizioni Zanichelli
- Mario Gliozzi, Storia della fisica, Edizioni Bollati Boringhieri
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su effetto fotoelettrico
Wikimedia Commons contiene immagini o altri file su effetto fotoelettrico
Collegamenti esterni[modifica | modifica wikitesto]
- Mauro Cappelli, effetto fotoelettrico, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
- (EN) photoelectric effect, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | Thesaurus BNCF 19365 · LCCN (EN) sh85101170 · GND (DE) 4174487-1 · J9U (EN, HE) 987007543512805171 · NDL (EN, JA) 00566101 |
|---|














![{\displaystyle E[J]=E[eV]\cdot 1.602176\cdot 10^{-19}\left[{\frac {J}{eV}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70d864855773d62e49cca8d469a5816ed5ce2fe5)

![{\displaystyle E[J]=hf}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9d616aa1b1b5e3cc1c1c3fc82703dfc4070e0b)

























