Superficie
 Piano |
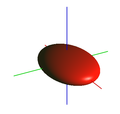 Ellissoide (Quadrica) |
 Sella (Grafico di una funzione) |
 Iperboloide (Superficie rigata) |
 Elicoide (Superficie minima) |
 Toro |
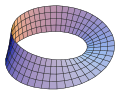 Nastro di Möbius (Superficie non orientabile) |
 Superficie di rotazione |
In matematica, una superficie è una forma geometrica senza spessore, avente solo due dimensioni. Una superficie può essere piatta (come un piano) o curva (come il bordo di una sfera o di un cilindro). Può essere limitata o illimitata, chiusa o aperta.
Vi sono diverse definizioni matematiche di superficie: queste sono tutte quante racchiuse nella nozione di "superficie astratta" e di varietà differenziabile. Nei casi più comuni il termine è usato per riferirsi a superfici in uno spazio tridimensionale.
Definizione[modifica | modifica wikitesto]
Informalmente una superficie è un oggetto geometrico ideale senza spessore, avente due dimensioni. Alcuni oggetti reali si avvicinano a questa nozione astratta: ad esempio una lamina molto sottile.
Formalmente, la definizione di superficie nello spazio richiede delle nozioni matematiche non banali proprie della geometria differenziale
Un sottoinsieme dello spazio euclideo tridimensionale è una superficie se per ogni punto contenuto in esistono un intorno aperto ed una funzione di classe
tale che interseca precisamente nei punti in cui si annulla:
e avente ovunque gradiente diverso da zero:
In altre parole, l'insieme è una superficie se è localmente esprimibile come luogo di zeri di una funzione. La condizione che il gradiente sia diverso da zero garantisce, tramite il teorema del Dini, che la superficie sia un oggetto liscio in ogni punto.
Costruzioni[modifica | modifica wikitesto]

oppure in forma implicita come luogo di zeri della funzione:
.
Una superficie può essere costruita in vari modi.
Forma parametrica[modifica | modifica wikitesto]
Una superficie può essere costruita come immagine di una funzione differenziabile iniettiva di due variabili reali nello spazio euclideo tridimensionale
dove è un insieme aperto del piano . Per ottenere un oggetto liscio, si richiede che il differenziale di sia anch'esso iniettivo in ogni punto : in altre parole deve essere una immersione.
Con questa costruzione le coordinate dei punti della superficie sono espresse agevolmente tramite le equazioni parametriche:
al variare dei due parametri nell'aperto .
Questa è la definizione generalmente più utile ai fini pratici, in quanto permette in modo agevole il calcolo di aree e di integrali di superficie.
Forma implicita globale[modifica | modifica wikitesto]

Una superficie può essere costruita globalmente come luogo di zeri di un'unica funzione differenziabile
detta equazione cartesiana. Per ottenere un oggetto liscio, il gradiente di deve essere diverso da zero in ogni punto di . Si noti che la definizione generale di superficie richiede l'esistenza di una tale funzione solo localmente.
Grafico di una funzione[modifica | modifica wikitesto]

Il grafico di una funzione differenziabile
definita su un aperto del piano cartesiano è una superficie.[1] La superficie può essere indicata in forma implicita tramite l'equazione
Nel caso in cui il dominio sia tutto il piano , la superficie è quindi il luogo di zeri della funzione implicita globale
La superficie può anche essere descritta in forma parametrica prendendo
Molte superfici però non sono grafico di funzioni, ad esempio la superficie sferica.
Superficie di rotazione[modifica | modifica wikitesto]
Una superficie di rotazione (o di rivoluzione) è ottenuta ruotando una curva intorno ad un asse. L'asse può essere uno dei tre assi cartesiani oppure una qualsiasi retta.
Concetti di base[modifica | modifica wikitesto]
Area[modifica | modifica wikitesto]

L'area di una superficie espressa in forma parametrica tramite una funzione con dominio è definita tramite gli strumenti del calcolo integrale nel modo seguente:
Nella formula sono presenti un integrale multiplo, le derivate parziali della funzione ed il prodotto vettoriale . In modo analogo è definito l'integrale di una funzione avente la superficie come dominio: questa operazione è chiamata integrale di superficie.
Normale[modifica | modifica wikitesto]
In ogni punto di una superficie è definito un piano tangente. Il piano tangente è descritto con gli strumenti forniti dall'algebra lineare e dal calcolo infinitesimale in più variabili.
Una normale in è un vettore perpendicolare al piano tangente, avente lunghezza unitaria. In ogni punto ha due normali, di verso opposto.
Curvatura[modifica | modifica wikitesto]

La curvatura è una proprietà fondamentale delle superfici nello spazio. In ogni punto della superficie vi sono due curvature principali e la curvatura gaussiana è definita come il prodotto di queste due quantità.
La curvatura gaussiana può essere positiva, nulla o negativa. In un piano, la curvatura è nulla e vale l'usuale geometria euclidea; su superfici a curvatura positiva o negativa è possibile definire delle geometrie non euclidee, chiamate rispettivamente ellittica e iperbolica. In queste geometrie, le usuali rette euclidee sono sostituite dalle geodetiche, curve sulla superficie che minimizzano (localmente) la distanza fra due punti.
Proprietà topologiche[modifica | modifica wikitesto]
La topologia è una branca della geometria che studia le proprietà degli oggetti geometrici che restano invariate quando viene effettuata una deformazione senza "strappi".

Genere[modifica | modifica wikitesto]
Il genere di una superficie è informalmente il "numero di manici" che questa contiene.
Orientabilità[modifica | modifica wikitesto]

Una superficie è orientabile se ha due facce (un "sopra" e un "sotto"), non orientabile altrimenti. Contrariamente a quanto suggerito dall'intuizione, esistono effettivamente superfici con una faccia sola: il prototipo è il nastro di Möbius.
Tipologia[modifica | modifica wikitesto]
Superfici algebriche[modifica | modifica wikitesto]
Una equazione polinomiale nelle tre variabili , come ad esempio
definisce una superficie algebrica. Affinché il luogo di zeri sia effettivamente una superficie liscia, il differenziale dell'equazione deve essere diverso da zero in ogni punto. Generalmente, si parla però comunque di "superficie algebrica" anche quando questa condizione non è soddisfatta: in questo caso si possono presentare punti non lisci detti singolarità.
Se il polinomio è di primo grado, la superficie è un piano. Superfici descrivibili con equazioni di 2º, 3º, 4º, 5º grado sono chiamate quadriche, cubiche, quartiche, quintiche e così via. La sestica mostrata in figura presenta alcune singolarità.
Quadriche[modifica | modifica wikitesto]
Una quadrica è una superficie algebrica di secondo grado. Le quadriche sono classificate con gli strumenti dell'algebra lineare (essenzialmente il teorema spettrale). Le quadriche non degeneri sono divise in cinque tipi:



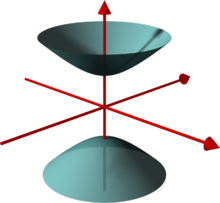
 Iperboloide a una falda
Iperboloide a una falda Iperboloide a due falde
Iperboloide a due falde
Superfici rigate[modifica | modifica wikitesto]
Una superficie è rigata se è unione di (infinite) rette.
Superfici minime[modifica | modifica wikitesto]
Una superficie è minima se ha area (localmente) minima fra tutte quelle che hanno un bordo fissato. Matematicamente, questa condizione equivale alla richiesta che la superficie abbia curvatura media ovunque nulla. In natura alcune strutture tendono a sistemarsi in modo da minimizzare l'area e formano quindi delle superfici minime.
Superfici chiuse[modifica | modifica wikitesto]
Una superficie è chiusa se è limitata e senza confini, come in una sfera. Con il linguaggio rigoroso della topologia, una superficie è chiusa se è compatta.[2]


 Bordo di un
Bordo di un
corpo con manici Toro annodato
Toro annodato
Generalizzazioni[modifica | modifica wikitesto]
Superficie astratta[modifica | modifica wikitesto]

In topologia, una branca importante della geometria, viene studiata una nozione più generale di superficie. La superficie studiata in questo ambito è un oggetto più astratto, che "vive di vita propria", non necessariamente contenuto nello spazio tridimensionale.
Formalmente, una superficie astratta è una varietà topologica di Hausdorff avente dimensione 2. Molte superfici astratte sono rappresentabili nello spazio, ma non tutte: ad esempio la bottiglia di Klein non è visibile dentro allo spazio tridimensionale (può però essere rappresentabile nello spazio euclideo quadridimensionale).
In molti contesti è più utile definire una superficie come varietà differenziabile invece che topologica. La differenza però non è sostanziale.
Altro esempio di superficie astratta (o algebrica) è la Superficie di Veronese, rappresentabile solamente in uno spazio proiettivo ad almeno cinque dimensioni, mentre la Tromba di Torricelli è un'altra superficie paradossale disegnabile in tre dimensioni.
Superfici immerse[modifica | modifica wikitesto]
Una superficie immersa è una superficie che può auto-intersecarsi. Più precisamente, è l'immagine di una immersione
di una superficie astratta . Si richiede quindi che abbia ovunque differenziale iniettivo: questa ipotesi garantisce che sia localmente iniettiva, ma non globalmente.

Ad esempio, la bottiglia di Klein è generalmente mostrata nello spazio tridimensionale tramite una immersione: la superficie si auto-interseca lungo una circonferenza. Un'altra superficie immersa è la superficie di Boy: in questo caso è un piano proiettivo reale, una superficie non orientabile che, come la bottiglia di Klein, non può essere contenuta nello spazio.
Superfici complesse[modifica | modifica wikitesto]
Nell'ambito della geometria complessa, una superficie complessa è una varietà complessa di dimensione 2. Si tratta di un oggetto completamente diverso dalla usuale superficie, poiché ha topologicamente dimensione reale 4.
Infine, a seconda dei contesti, si può indicare col termine superficie strutture con caratteristiche diverse da quelle citate sopra; ad esempio, si può chiamare brevemente superficie un'ipersuperficie in uno spazio euclideo (o in una varietà differenziabile), cioè una varietà di dimensione inferiore a quella dello spazio ambiente (ma non necessariamente 2), talvolta si parla anche di superfici frattali, indicando strutture frattali costruite a partire da una superficie, ma che, in definitiva, non ne conservano alcuna caratteristica specifica.
Teoremi[modifica | modifica wikitesto]
Teorema di Gauss-Bonnet[modifica | modifica wikitesto]
Teorema di Stokes[modifica | modifica wikitesto]
Classificazione topologica delle superfici[modifica | modifica wikitesto]
Le superfici compatte sono classificate in topologia a meno di omeomorfismo da tre parametri: il genere, il numero di componenti di bordo, e l'orientabilità.
In topologia vengono considerate spesso anche le superfici di tipo finito, ottenute a partire dalle superfici compatte rimuovendo un numero finito di punti e creando così delle punture. Una superficie con punture non è mai compatta. Analogamente alle superfici compatte, quelle di tipo finito sono classificate da quattro parametri: il genere, il numero di componenti di bordo, l'orientabilità e il numero di punture.
Teorema di uniformizzazione[modifica | modifica wikitesto]
Note[modifica | modifica wikitesto]
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «superficie»
Wikizionario contiene il lemma di dizionario «superficie» Wikimedia Commons contiene immagini o altri file sulla superficie
Wikimedia Commons contiene immagini o altri file sulla superficie
Collegamenti esterni[modifica | modifica wikitesto]
- superficie, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) surface, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (FR) Esempi di superfici da Mathcurve, Encyclopédie des formes mathématiques remarquables
| Controllo di autorità | Thesaurus BNCF 21329 · LCCN (EN) sh00005762 · J9U (EN, HE) 987007292879305171 · NDL (EN, JA) 00567234 |
|---|

























































