Ellissoide
Da Wikipedia, l'enciclopedia libera.
In geometria, per ellissoide si intende il tipo di quadrica che costituisce l'analogo tridimensionale della ellisse nelle due dimensioni.
Indice |
[modifica] Definizione
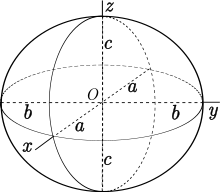
L'equazione dell'ellissoide standard in un sistema di coordinate cartesiane Oxyz è
,
dove a, b e c sono numeri reali positivi fissati che determinano la forma dell'ellissoide. Se due di questi numeri sono uguali, l'ellissoide si dice sferoide o ellissoide di rotazione; se tutti e tre sono uguali, abbiamo una sfera.
Se ci limitiamo a considerare le possibilità consentite da 
, abbiamo la seguente casistica:
, si ha un ellissoide scaleno;
, si ha uno sferoide prolato (a forma di sigaro);
, si ha uno sferoide oblato (a forma di lenticchia);
, si ha un ellissoide piatto (due ellissi incollate)
, si ha una sfera, come già segnalato.
Si definiscono assi centrali di inerzia gli assi di simmetria dell'ellissoide che formano un sistema di riferimento centrato nel baricentro dell'ellissoide.
[modifica] Parametrizzazione
Utilizzando le comuni coordinate, dove 
è un punto di latitudine riduzione, o parametrico, e 
è la sua longitudine planetographic, un ellissoide può essere parametrizzato per:
-
-
-
- (Si noti che questa non è parametrizzazione
- 1-1 ai poli, dove
)
-
Oppure, utilizzando il sistema di coordinate sferica, dove 
è il colatitude, o zenit, e 
è la longitudine di 360°, o azimuth:
[modifica] Volume
Il volume di un'ellissoide si ottiene semplicemente da quello di una sfera e dall'effetto delle omotetie: 
[modifica] Area superficiale
L'area superficiale, invece, è fornita da espressioni molto più elaborate. Una espressione esatta è:
dove:
mentre 
, 
denotano gli integrali ellittici incompleti di primo e secondo genere rispettivamente.
Sono disponibili anche espressioni approssimate:
- ellissoide piatto:
- sferoide prolato:
- sferoide oblato:
- ellissoide scaleno:
Se si utilizza p = 1,6075 si ha un errore relativo al più dell'1,061% (formula di Knud Thomsen); un valore p = 8/5 = 1,6 è ottimale per gli ellissoidi quasi sferici e presenta un errore relativo inferiore all'1,178% (formula di David W. Cantrell).
[modifica] Manipolazioni lineari
Se si applica una trasformazione lineare invertibile ad una sfera, si ottiene un'ellissoide; in conseguenza del teorema spettrale questo ellissoide si può ricondurre alla forma standard.
L'intersezione di un ellissoide con un piano può essere o l'insieme vuoto, o un insieme contenente un singolo punto, o una ellisse.
[modifica] Dimensioni superiori
Si può anche definire un ellissoide in più di 3 dimensioni, come immagine di un'ipersfera sottoposta ad una trasformazione lineare invertibile. Il teorema spettrale garantisce ancora la possibilità di ottenere una equazione standard della forma
.
