Seno (matematica)

In matematica, in particolare in trigonometria, dato un triangolo rettangolo il seno di uno dei due angoli interni adiacenti all'ipotenusa è definito come il rapporto tra le lunghezze del cateto opposto all'angolo e dell'ipotenusa.
Più in generale il seno di un angolo , espresso in gradi o radianti, è una quantità che dipende solo da , costruita usando la circonferenza unitaria.
Definendo come il seno nell'angolo si ottiene la funzione seno, una funzione trigonometrica di fondamentale importanza nell'analisi matematica. In ambito italiano questa funzione viene spesso indicata con .
Definizione[modifica | modifica wikitesto]
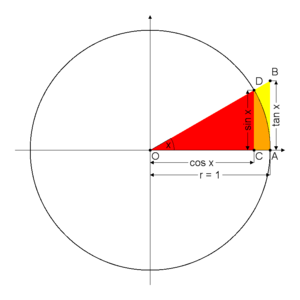
Nel triangolo rosso in figura, il seno di è dato da
Più in generale si definisce il seno di un angolo a partire dalla circonferenza goniometrica, ovvero dalla circonferenza di raggio unitario nel piano cartesiano. Presa la semiretta uscente dall'origine che forma un angolo con l'asse delle ascisse come in figura, il seno dell'angolo è quindi definito come il valore della coordinata del punto di intersezione tra la semiretta e la circonferenza (in figura, è la lunghezza del segmento ).
Il dominio della funzione seno è l'insieme dei numeri reali, mentre l’immagine è l'intervallo reale , ossia applicando tale funzione a tutti i numeri reali si ottengono tutti i numeri reali compresi tra e , estremi inclusi.
La tabella seguente elenca i principali valori notevoli assunti dalla funzione seno:[1][2]
| in radianti | 0 | ||||||||||
| in gradi | 0° | 15° | 18° | 30° | 45° | 60° | 75° | 90° | 180° | 270° | 360° |
Nei testi di matematica il seno di è solitamente indicato con la notazione oppure , ove è un'abbreviazione del latino sinus usata anche nei paesi di lingua inglese.
Esiste un'altra definizione di seno che si collega alle rotazioni: il seno di un angolo è la componente lungo l'asse delle ordinate del versore , versore dell'asse delle ascisse, ruotato di .
Funzione seno[modifica | modifica wikitesto]
La funzione seno è definita associando ad il seno dell'angolo in radianti, ed è indicata con . Poiché e definiscono lo stesso angolo, la funzione seno è una funzione periodica di periodo , dove è l'angolo giro.


Seno e coseno[modifica | modifica wikitesto]
Tra seno e coseno esiste la relazione fondamentale:
che è conseguenza del teorema di Pitagora. Infatti nel triangolo nella seconda figura il coseno di è definito come
D'altra parte il teorema di Pitagora applicato al triangolo fornisce la relazione
e quindi
Vale anche la relazione:
Come per il coseno, la cosecante di un angolo è diviso il seno dell'angolo.
Proprietà analitiche della funzione seno[modifica | modifica wikitesto]
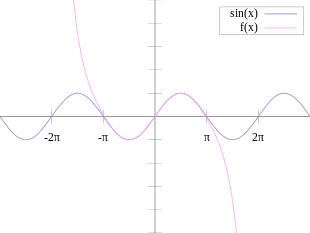
La derivata della funzione seno è la funzione coseno:[3]
La derivata seconda è invece
La funzione seno è una funzione analitica, la cui espansione in serie di Taylor è
In analisi matematica questa uguaglianza è spesso usata per definire il seno. La stessa serie definisce il seno come funzione olomorfa su tutto il piano complesso.
Equazioni fondamentali relative al seno[modifica | modifica wikitesto]
Seguono alcune equazioni fondamentali riguardanti la funzione seno:[4]
con l'aggiunta della condizione che:
Esiste anche un'identità trigonometrica che mette in relazione la funzione seno alla funzione tangente:
Questa identità si rivela di fondamentale importanza nella risoluzione di equazioni goniometriche in cui l'incognita figuri come argomento sia di un seno sia di un coseno o di funzioni derivate da queste. Esiste infatti un'analoga identità per quanto riguarda il coseno e l'uso congiunto di queste due identità permette la risoluzione dell'equazione nell'incognita .
Definizioni correlate[modifica | modifica wikitesto]
Il reciproco del seno, definito dove il seno è diverso da zero, è la cosecante:[5]
La funzione seno ristretta all'intervallo come dominio e con codominio è biettiva, e quindi ha un’inversa, chiamata arcoseno e indicata con o con che riprende la notazione della funzione inversa.[6] Per definizione si ha quindi:
Altre proprietà[modifica | modifica wikitesto]
Dalla formula di Eulero si deduce che la funzione seno è in relazione con la funzione esponenziale e con la funzione seno iperbolico. Infatti per ogni numero reale si ha
Alcune formule particolari riguardanti la funzione seno coinvolgono l'operazione di prodotto.
Per esempio risulta per ogni intero
In analisi complessa, applicando teorema di fattorizzazione di Weierstrass alla funzione seno, la si può esprimere come prodotto infinito, mediante la seguente formula che vale per ogni numero complesso
Un altro prodotto infinito mette in relazione il seno e il coseno:
La funzione seno è anche in relazione con alcune funzioni speciali, come si evince, per esempio, dalla formula di riflessione della funzione Gamma
e dall'equazione funzionale soddisfatta dalla funzione zeta di Riemann
Un'altra relazione tra funzione seno e funzione Gamma è data dal seguente integrale definito, valido per :[7]
Infine, mediante la formula della frazione continua di Eulero è possibile esprimere la funzione seno sotto forma di frazione continua:[7][8]
Storia e origine del nome[modifica | modifica wikitesto]
Il concetto di seno fu introdotto dal matematico e astronomo indiano Aryabhata I (in devanāgarī: आर्यभट) nella sua opera Aryabhatiya (499).[9]
Il seno è per definizione la metà di una corda, cioè un segmento che unisce due punti (detti estremi) di una circonferenza. In sanscrito, "metà corda" è reso con jya-ardha, a volte sostituito con ardha-jya e abbreviato in jya "corda". Questo termine fu importato nella lingua araba come jiba, un termine senza significato prima di allora, ma che rifletteva la pronuncia del nome jya. Secondo le regole della lingua araba, questo nome venne scritto con le due consonanti jb, senza vocali. Successivamente, quando i traduttori occidentali attinsero alle fonti arabe, interpretarono la parola jb come jaib, il cui significato era "baia". Infine l'italiano Gherardo da Cremona (1114 - 1187) tradusse la parola in latino come sinus, il cui significato era appunto "baia".
Note[modifica | modifica wikitesto]
- ^ Valori delle funzioni goniometriche, su youmath.it, YouMath. URL consultato il 19 ottobre 2016.
- ^ esercizimatematica.com, https://www.esercizimatematica.com/tabella-seno-coseno-con-tutti-gli-angoli/.
- ^ Derivata del seno, su youmath.it, YouMath. URL consultato il 19 ottobre 2016.
- ^ Formule trigonometriche, su youmath.it, YouMath. URL consultato il 19 ottobre 2016.
- ^ secante, in Enciclopedie on line, Treccani. URL consultato il 19 ottobre 2016.
- ^ arcoséno, in Enciclopedie on line, Treccani. URL consultato il 19 ottobre 2016.
- ^ a b Wolfram Mathworld - Sine, su mathworld.wolfram.com. URL consultato il 9 aprile 2020.
- ^ Mauro Fiorentini - Funzioni espresse tramite frazioni continue, su bitman.name. URL consultato il 10 aprile 2020.
- ^ Aryabhata, su pls.dima.unige.it. URL consultato il 19 ottobre 2016.
Voci correlate[modifica | modifica wikitesto]
- Funzione trigonometrica
- Sinusoide
- Coseno
- Tangente (matematica)
- Arcoseno
- Circonferenza goniometrica
- Formula di Eulero
- Formule di duplicazione
- Formule di bisezione
- Formule di prostaferesi
- Formule di Werner
- Teorema dei seni
- Funzione periodica
- Funzione alternata
- Seno iperbolico
- Muḥammad ibn Jābir al-Ḥarrānī al-Battānī
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sul seno
Wikimedia Commons contiene immagini o altri file sul seno
Collegamenti esterni[modifica | modifica wikitesto]
- seno, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- SENO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1936.
- seno, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- séno², su sapere.it, De Agostini.
- seno, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) sine, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Seno, su MathWorld, Wolfram Research.
- (EN) Seno, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
| Controllo di autorità | Thesaurus BNCF 64504 |
|---|







![{\displaystyle [-1;+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90f1555bbff659d4d69b48a914890f5df95f2a0)







































![{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














