Teoria di Kaluza-Klein
La teoria di Kaluza-Klein rappresenta un tentativo di unificazione del campo gravitazionale, descritto dalle equazioni della relatività generale, con il campo elettromagnetico, descritto dalle equazioni di Maxwell, attraverso l'introduzione di una quarta dimensione spaziale in aggiunta alle tre conosciute più una temporale, per un totale di cinque dimensioni.
Origine[modifica | modifica wikitesto]
La teoria venne elaborata dal matematico Theodor Kaluza e sottoposta nel 1919 al parere di Albert Einstein. Questi, dopo un'iniziale sottovalutazione, incoraggiò il giovane autore a curare la pubblicazione della teoria, cosa che avvenne per la prima volta nel 1921[1].
Precedenti[modifica | modifica wikitesto]
L'idea di sviluppare la teoria della gravitazione e le equazioni di Maxwell nel contesto di uno spazio pentadimensionale era già stata introdotta nel 1914 dal fisico finlandese Gunnar Nordström (1881-1923) nel suo tentativo di fondare due proprie teorie della gravitazione, importanti concorrenti della sintesi einsteiniana. Al giorno d'oggi le sue teorie rivestono una importanza storica e didattica, sebbene si siano rivelate in disaccordo con i dati sperimentali. L'originale intuizione in esse contenute cadde tuttavia presto nel dimenticatoio, anche a seguito della prematura morte dell'autore.
Le equazioni di campo unificato[modifica | modifica wikitesto]
Le equazioni risultanti dalla teoria possono venire divise in due insiemi: uno equivalente alle equazioni di campo di Einstein, l'altro equivalente alle equazioni del campo elettromagnetico di Maxwell, con l'aggiunta di un ulteriore campo scalare denominato radion.
Problemi[modifica | modifica wikitesto]
Uno dei risvolti problematici della teoria era costituito dalla non osservabilità della quinta dimensione congetturata. In effetti l'universo in cui viviamo ci appare quadridimensionale e, a tutt'oggi, in attesa di nuovi dati sperimentali provenienti dal Large Hadron Collider di Ginevra, i dispositivi sperimentali disponibili non sono stati in grado di rivelare l'esistenza di eventuali dimensioni aggiuntive.
La soluzione di Oskar Klein[modifica | modifica wikitesto]
Una possibile soluzione del paradosso fu proposta nel 1926 dal fisico svedese Oskar Klein (da non confondere con il matematico tedesco Felix Klein) che congetturò innanzitutto che la quarta dimensione spaziale non si estendesse all'infinito ma fosse 'arrotolata' su se stessa a costituire in ciascun punto uno spazio compatto, nella fattispecie un cerchio. La compattificazione così proposta consente alla dimensione aggiuntiva di estendersi, a differenza di quelle ordinarie, su distanze finite. L'invisibilità della dimensione aggiuntiva può essere allora spiegata solo se si accoglie l'ulteriore ipotesi che la compattificazione della dimensione extra avvenga su scala così piccola da sfuggire alla sensibilità degli strumenti disponibili.
Un esempio di dimensione aggiuntiva compattificata in due dimensioni[modifica | modifica wikitesto]
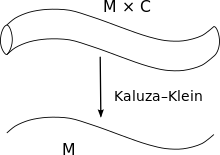
La situazione può essere spiegata meglio immaginando di partire da uno spazio illimitato, ma dotato di una sola dimensione spaziale anziché tre, come ad esempio una retta. L'aggiunta di una dimensione compattificata a formare un cerchio renderà lo spazio così costruito simile ad un tubo cilindrico che si estenda indefinitamente nei due versi della retta. In effetti lo spazio risultante da un punto di vista topologico è omeomorfo ad un cilindro infinito in entrambi i versi.
Uno spazio così formato è alla portata della nostra immaginazione in quanto esso può essere immerso nello spazio ordinario, è cioè omeomorfo ad un sottospazio dello spazio ordinario. Una sua porzione finita è facilmente assimilabile ad un lungo tubo sospeso tra due rocce che, osservato da notevole distanza, appare ad occhio nudo come filiforme ed esteso in un'unica dimensione, la lunghezza. Solo osservato con uno strumento più potente dell'occhio, come ad esempio un binocolo, esso apparirà come una strisciolina, rivelando il suo spessore e la sua estensione in due dimensioni.
In equilibrio su un sottile universo[modifica | modifica wikitesto]
Una persona che camminasse in equilibrio su un simile tubo, se molto sottile, sarebbe in grado di sperimentare con i piedi una sola dimensione: la lunghezza filiforme sotto di lui. Per contro, un essere di dimensioni confrontabili alla sezione del tubicino, un piccolissimo insetto ad esempio, sarebbe in grado di fare tutti i movimenti permessi dalla combinazione del movimento rotatorio intorno al tubo e di quello lungo il tubo. Grazie alle piccole dimensioni, sarebbe insomma in grado di sfruttare, e soprattutto di percepire, la bidimensionalità della superficie del tubo.
Allo stesso modo se noi potessimo rimpicciolirci a dimensioni paragonabili a quelle della distanza su cui è arrotolata (compattificata) la dimensione extra, riusciremmo a muoverci non solo nelle tre dimensioni spaziali a noi note, ma anche nella dimensione aggiuntiva in una situazione che per il nostro cervello, evolutosi sulla usuale scala dimensionale, è impossibile da concepire.
Il modello di Klein[modifica | modifica wikitesto]

Secondo l'interpretazione di Klein si può trasporre lo stesso ragionamento alla situazione delle dimensioni extra prospettate dalla teoria. Noi, trovandoci ad una scala estremamente più grande rispetto a quella in cui le dimensioni si fanno per così dire "sentire", riusciamo a vedere solo le tre dimensioni spaziali infinitamente estese. In questo senso si può dire che la dimensione extra è "nascosta" ai nostri sensi.
C'è una differenza fondamentale con la realtà prospettata dalla teoria: l'esempio del tubo è solo un'approssimazione di uno spazio cilindrico bidimensionale indefinitamente esteso. Inoltre si tenga conto che, a differenza di quello dell'esempio, lo spazio immaginato da Kaluza con inclusa la dimensione aggiuntiva non è immerso in uno spazio esterno, ma rappresenta esso stesso tutto lo spazio, tutto l'universo esistente: non vi è alcun spazio esterno in cui un osservatore possa trovarsi a guardarlo.
L'abbandono della teoria[modifica | modifica wikitesto]
La teoria di Kaluza-Klein era un tentativo di unificazione comunque confinato in un orizzonte classico della fisica. Non rendeva conto di alcuni aspetti della realtà quali la quantizzazione della carica.
Per questo motivo, dopo l'iniziale interesse della comunità dei fisici, il modello di unificazione in 5 dimensioni fu abbandonato e cadde per anni nell'oblio.
Il ritorno in auge[modifica | modifica wikitesto]

I tentativi di fondare una teoria di unificazione consistente hanno dato luogo a un lungo lavoro teorico ancora lontano dal concludersi.
Tra i percorsi teorici esplorati, nessuno coronato dal successo, vi è la Teoria delle stringhe che, fattasi strada dagli anni '60, ha inaspettatamente recuperato la congettura delle dimensioni aggiuntive "nascoste" dell'universo facendo tornare in auge i pionieristici lavori precedenti.
Nella moderna teoria delle stringhe e nella contigua M-teoria si ipotizza l'esistenza di sei dimensioni spaziali aggiuntive, compattificate non in semplici cerchi, sfere o ipersfere, ma nell'infinita varietà di forme topologicamente più esotiche e polimorfiche degli spazi di Calabi-Yau compatti.
Note[modifica | modifica wikitesto]
- ^ Theodor Kaluza. Op. cit. in Bibliografia, 1921.
Bibliografia[modifica | modifica wikitesto]
Testi divulgativi[modifica | modifica wikitesto]
- Particelle,stringhe e altro di Warren Siegel, Di Renzo Editore (2008), ISBN 88-8323-204-6.
- L'Universo Elegante di Brian Greene, Einaudi (2000), ISBN 88-06-15523-7.
- La Trama del Cosmo di Brian Greene, Einaudi (2004), ISBN 88-06-18091-6.
- La Materia-Specchio di Robert Foot, Macro Edizioni (2005) ISBN 88-7507-448-8.
- Un Universo Diverso di Robert Laughlin, Codice Edizioni (2006) ISBN 88-7578-033-1.
- Il Cervello Quantico di Jeffrey Satinover, Macro Edizioni (2002) ISBN 88-7507-408-9.
- Il Giardino delle Particelle di Gordon Kane, Tea Edizioni (1997) ISBN 88-502-0125-7.
- Il Paesaggio Cosmico: Dalla teoria delle stringhe al megaverso di Leonard Susskind, Adelphi (2006), ISBN 88-459-2153-0.
- Neanche sbagliata. Il fallimento della teoria delle stringhe e la corsa all'unificazione delle leggi della fisica. di Peter Woit, Codice Edizioni, (2007) ISBN 88-7578-072-2.
- Rischiare con Dio (dopo Einstein) di Antonino Palumbo, Edizioni Scientifiche Italiane, (2006), ISBN 88-495-1257-0.
- L'Unificazione della Conoscenza di Antonino Palumbo, Edizioni Scientifiche Italiane, (2008), ISBN 978-88-495-1745-3.
- Passaggi curvi di Lisa Randall, ilsaggiatore, (2008), ISBN 978-88-565-0072-1.
Manuali[modifica | modifica wikitesto]
- Gunnar Nordström, Uber die Möglichkeit, das elektromagnetische Feld und das Gravitationsfeld zu vereinigen (Sulla possibilità di unificare i campi elettromagnetici e gravitazionali), Physik. Zeitschr., 15, 504-506, (1914).
- Theodor Kaluza, On the problem of unity in physics, Sitzungsber Preuss. Akad. Wiss, Berlin. (Math. Phys.), 966-972, (1921).
- Oskar Klein, Quantum theory and five dimensional theory of relativity, Z. Phys., 37, 895-906 (1926).
- Michael Green, John Schwarz and Edward Witten, Superstring theory, Cambridge University Press (1987). Il libro di testo originale.
- Vol. 1: Introduction, ISBN 0-521-35752-7.
- Vol. 2: Loop amplitudes, anomalies and phenomenology, ISBN 0-521-35753-5.
- Johnson, Clifford, D-branes, Cambridge University Press (2003). ISBN 0-521-80912-6.
- Joseph Polchinski, String Theory, Cambridge University Press (1998). Un testo moderno.
- Vol. 1: An introduction to the bosonic string, ISBN 0-521-63303-6.
- Vol. 2: Superstring theory and beyond, ISBN 0-521-63304-4.
- Zwiebach, Barton, A First Course in String Theory., Cambridge University Press (2004), ISBN 0-521-83143-1. Sono disponibili correzioni online.
Voci correlate[modifica | modifica wikitesto]
- Campo elettromagnetico
- Dimensione compattata
- Dimensione extra
- Grado di libertà (meccanica classica)
- M-teoria
- M-teoria (versione semplificata)
- Oskar Klein
- Relatività generale
- Teoria delle stringhe
- Teoria delle superstringhe
- Theodor Kaluza
- Azione Nambu-Goto
- Computer quantistico
- AdS/CFT
- D-brane
- Gravità quantistica
- Gravità quantistica a loop
- Gravitone
- K-teoria ritorta
- Principio di indeterminazione di Heisenberg
- Stringa (fisica)
- Supergravità
- Supersimmetria
- Teoria del campo conforme
- Teoria del tutto
- Teoria F
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Teoria di Kaluza-Klein
Wikimedia Commons contiene immagini o altri file su Teoria di Kaluza-Klein
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Kaluza-Klein Theories, su th.physik.uni-frankfurt.de. URL consultato il 21 giugno 2007 (archiviato dall'url originale il 17 maggio 2007).
- Tutto sulle stringhe (incluso un test di autovalutazione) in ScienzaPerTutti, su scienzapertutti.lnf.infn.it.
- (EN) The Official String Theory Web Site - Ottimo sito di divulgazione, contiene anche un apparato matematico utile agli esperti, su superstringtheory.com.
- (EN) PLANCK Home page, su aether.lbl.gov.
- (EN) Risultati del WMAP, su map.gsfc.nasa.gov.
- (EN) Superstringtheory.com - Guida online.
- (EN) Beyond String Theory - Progetto in corso che spiega molti aspetti della teoria delle stringhe e gli argomenti correlati.
- (EN) The Elegant Universe - Documentario NOVA di Brian Greene. Varie immagini, testi, video ed animazioni sulla teoria delle stringhe.
- (EN) The Symphony of Everything: a short interactive introduction to string theory., su msnbc.com. URL consultato il 14 ottobre 2010 (archiviato dall'url originale il 24 settembre 2008).
- (EN) "Cosmic strings reborn?" di Tom Kibble, conferenza del September 2004.
- (EN) SCI.physics.STRINGS - La home page di un newsgroup dedicato alla teoria delle stringhe.
- (EN) Resource Letter - Una buona guida per studenti alla letteratura sulla teoria delle stringhe.
- (EN) Superstrings! String Theory Home Page - Tutorial online.
- (EN) A popular blog on string theory, su math.columbia.edu.
- (EN) Is string theory even wrong? - Critica alla teoria delle stringhe.
| Controllo di autorità | LCCN (EN) sh86006241 · GND (DE) 4224276-9 · BNF (FR) cb12290058z (data) · J9U (EN, HE) 987007565948805171 |
|---|