Matematica e architettura: differenze tra le versioni

Da Wikipedia, l'enciclopedia libera.
Vai alla navigazione Vai alla ricerca
Differenza successiva →
Contenuto cancellato Contenuto aggiunto
VisualeWikitesto
Creata dalla traduzione della pagina "Mathematics and architecture"
(Nessuna differenza)

Versione delle 12:11, 1 lug 2020

"The Gherkin", [1] 30 St Mary Axe, Londra, completato nel 2003, è un solido di rotazione progettato parametricamente .
Il tempio di Kandariya Mahadeva (1030 circa), Khajuraho, India, è un esempio di architettura religiosa con una struttura simile a un frattale che ha molte parti che assomigliano al tutto. [2]

Matematica e architettura sono correlate, poiché, come con altre arti, gli architetti usano la matematica per diverse ragioni. Oltre alla matematica necessaria per la progettazione di edifici, gli architetti usano la geometria per definire la forma spaziale di un edificio, dai Pitagorici del VI secolo a.C. in poi, per creare forme considerate armoniose, e quindi per disporre gli edifici e l'ambiente circostante secondo principi matematici, estetici e talvolta religiosi, decorare edifici con oggetti matematici come tessellazioni e per raggiungere obiettivi ambientali, come ridurre al minimo la velocità del vento attorno alle basi di edifici molto alti.

Nell'antico Egitto, nell'antica Grecia, in India e nel mondo islamico, furono costruiti edifici come piramidi, templi, moschee, palazzi e mausolei con proporzioni specifiche per motivi religiosi. Nell'architettura islamica, forme geometriche e motivi geometrici nella piastrellatura sono utilizzati per decorare edifici, sia all'interno che all'esterno. Alcuni templi indù hanno una struttura simile a un frattale in cui le parti assomigliano al tutto, trasmettendo un messaggio sull'infinito nella cosmologia indù. Nell'architettura cinese, i tulou della provincia del Fujian sono strutture difensive circolari e comuni. Nel XXI secolo, gli ornamenti matematici vengono nuovamente utilizzati per coprire edifici pubblici.

Nell'architettura rinascimentale, la simmetria e la proporzione sono state deliberatamente enfatizzate da architetti come Leon Battista Alberti, Sebastiano Serlio e Andrea Palladio, influenzati dal De architectureura di Vitruvio dell'antica Roma e dall'aritmetica dei Pitagorici dell'antica Grecia. Alla fine del XIX secolo, Vladimir Shukhov in Russia e Antoni Gaudí a Barcellona furono i pionieri nell'uso delle strutture iperboloidi. Nella Sagrada Família, Gaudí incorporava anche paraboloidi iperbolici, tessellazioni, archi di catenaria, catenoidi, elicoidi e superfici rigate. Nel XX secolo, stili come l'architettura moderna e il decostruttivismo hanno esplorato diverse geometrie per ottenere gli effetti desiderati. Superfici minime sono state sfruttate in coperture simili a tende come all'aeroporto internazionale di Denver, mentre Richard Buckminster Fuller ha aperto la strada all'uso delle forti strutture a guscio sottile note come cupole geodetiche.

Campi collegati

Nel Rinascimento, un architetto come Leon Battista Alberti avrebbe dovuto essere esperto in molte discipline, tra cui l' aritmetica e la geometria .

Gli architetti Michael Ostwald e Kim Williams, considerando i rapporti tra architettura e matematica, notano che i campi come comunemente intesi potrebbero sembrare collegati solo debolmente, poiché l'architettura è una professione che si occupa della questione pratica della costruzione di edifici, mentre la matematica è puro studio del numero e di altri oggetti astratti. Ma, sostengono, le due sono fortemente collegate e lo sono state fin dall'antichità. Nell'antica Roma, Vitruvio descriveva un architetto come un uomo che conosceva abbastanza una gamma di altre discipline, in primo luogo la geometria, per consentirgli di supervisionare abili artigiani in tutte le altre aree necessarie, come muratori e carpentieri. Lo stesso dicasi nel Medioevo, dove i laureati imparavano l' aritmetica, la geometria e l' estetica accanto al programma di base di grammatica, logica e retorica (il trivio) in eleganti sale realizzate da maestri costruttori che avevano guidato molti artigiani. A un capomastro ai vertici della sua professione era assegnato il titolo di architetto o ingegnere. Nel Rinascimento, il quadrivio di aritmetica, geometria, musica e astronomia divenne un programma extra atteso dall'uomo rinascimentale come Leon Battista Alberti. Allo stesso modo in Inghilterra, Sir Christopher Wren, oggi noto come architetto, fu inizialmente un noto astronomo. [3]

Williams e Ostwald, analizzando ulteriormente l'interazione tra matematica e architettura, dal 1500, secondo l'approccio del sociologo tedesco Theodor Adorno, identificano tre tendenze tra gli architetti, vale a dire: essere rivoluzionari, introdurre idee completamente nuove e reazionarie, non riuscendo a introdurre il cambiamento o revivalisti, in realtà andando indietro. Sostengono che gli architetti hanno evitato di guardare alla matematica come fonte di ispirazione nei tempi del risveglio. Ciò spiegherebbe perché nei periodi revivalisti, come il revival gotico nell'Inghilterra del XIX secolo, l'architettura avesse scarse connessioni con la matematica. Allo stesso modo, notano che in tempi reazionari come il Manierismo italiano, tra il 1520 e il 1580 circa, o i movimenti barocco e palladiano, del XVII secolo, la matematica era a malapena consultata. Al contrario, i movimenti rivoluzionari dell'inizio del XX secolo, come il futurismo e il costruttivismo, respinsero attivamente vecchie idee, abbracciando la matematica e portando all'architettura modernista. Verso la fine del XX secolo, anche la geometria frattale fu rapidamente conquistata dagli architetti, così come la piastrellatura aperiodica, per fornire interessanti e attraenti coperture per gli edifici. [4]

Gli architetti usano la matematica per diversi motivi, tralasciando l'uso necessario della matematica nell'ingegneria degli edifici. [5] In primo luogo, usano la geometria perché definisce la forma spaziale di un edificio. [6] In secondo luogo per progettare forme che sono considerate belle o armoniose. [7] Dal tempo dei Pitagorici con la loro filosofia religiosa del numero, [8] architetti nell'antica Grecia, nell'antica Roma, nel mondo islamico e nel Rinascimento italiano hanno scelto le proporzioni dell'ambiente costruito - edifici e dintorni progettati - secondo la matematica così come principi estetici e talvolta religiosi. [9] [10] [11] [12] In terzo luogo, possono usare oggetti matematici come tessellazioni per decorare gli edifici. [13] [14] In quarto luogo, possono utilizzare la matematica sotto forma di modellistica computerizzata per raggiungere obiettivi ambientali, in modo da ridurre al minimo le correnti d'aria vorticose alla base di edifici molto alti. [1]

Estetica profana

Antica Roma

Pianta di una casa greca di Vitruvio

Vitruvio

L'interno del Pantheon di Giovanni Paolo Panini, 1758

L'influente architetto romano Vitruvio sostenne che la progettazione di un edificio, come quella di un tempio,dipende da due qualità, proporzione e simmetria. La proporzione garantisce che ogni parte di un edificio sia collegata armoniosamente a ogni altra. La simmetria nell'uso di Vitruvio significa qualcosa di più vicino al termine inglese modularità rispetto alla simmetria a specchio, poiché si riferisce ancora all'assemblaggio di parti (modulari) nell'intero edificio. Nella sua Basilica di Fano, usa rapporti di piccoli numeri interi, in particolare i numeri triangolari (1, 3, 6, 10,   ...) per proporzionare la struttura in moduli (vitruviani) . [N 1] Pertanto la larghezza della Basilica rispetto alla lunghezza è 1: 2; la navata laterale è alta quanto larga, 1:1; le colonne hanno un diametro di 1,5 metri e un'altezza di 15, 1:10. [9]

Pianta del Pantheon

Vitruvio nominò tre qualità richieste per l'architettura nel suo De architectureura, c. 15 a.C.: stabilità, utilità (o "merce" nell'inglese di Henry Wotton del XVI secolo) e delizia. Queste possono essere usate come categorie per classificare i modi in cui la matematica è usata in architettura. La stabilità prevede l'uso della matematica per garantire che un edificio si elevi, quindi gli strumenti matematici utilizzati nella progettazione e per supportare la costruzione, ad esempio per garantire stabilità e modellare le strutture. L'utilità deriva in parte dall'efficace applicazione della matematica, dal ragionamento e dall'analisi delle relazioni spaziali e di altro tipo in un progetto. La delizia è un attributo dell'edificio risultante, derivante dall'incarnazione delle relazioni matematiche nella progettazione; comprende qualità estetiche, sensoriali e intellettuali. [16]

Il Pantheon

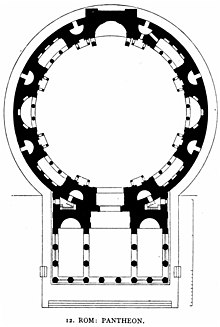
Il Pantheon di Roma è sopravvissuto intatto, illustrando la struttura romana classica, la proporzione e la decorazione. La struttura principale è una cupola, con la sommità lasciata aperta come un occhio circolare per far entrare la luce; ha una facciata con un breve colonnato e frontone triangolare. L'altezza dell'occhio e il diametro della pianta interna sono uguali, 43,3 metri (142 ft), quindi l'intero interno si adatterebbe esattamente all'interno di un cubo e potrebbe ospitare una sfera dello stesso diametro. [17] Queste dimensioni hanno più senso quando espresse in antiche unità di misura romane: la cupola si estende su 150 piedi romani [N 2] ); l'occhio ha un diametro di 30 piedi romani, la porta d'ingresso è alta 40 piedi romani. [18] Il Pantheon rimane la più grande cupola del mondo in cemento non armato. [19]

Rinascimento

Facciata di Santa Maria Novella, Firenze, 1470. Il fregio con quadrati è di Leon Battista Alberti .

Il primo trattato rinascimentale sull'architettura fu il De re aedificatoria di Leon Battista Alberti (sull'arte della costruzione) del 1450 e divenne il primo libro stampato sull'architettura nel 1485. Si basava in parte sul De architectureura di Vitruvio e, tramite Nicomaco, sull'aritmetica di Pitagora. Alberti inizia con un cubo e ne ricava rapporti. Quindi la diagonale di una faccia dà il rapporto 1: √ 2, mentre il diametro della sfera che circoscrive il cubo dà 1: √ 3 . [20] [21] Alberti ha anche documentato la scoperta di Filippo Brunelleschi della prospettiva lineare, sviluppata per consentire la progettazione di edifici che apparirebbero magnificamente proporzionati se visti da una distanza conveniente. [12]

Prospettiva architettonica di un palcoscenico allestito da Sebastiano Serlio, 1569 [22]

Il successivo testo importante fu Regole generali d'architettura di Sebastiano Serlio. Il primo volume apparve a Venezia nel 1537 e il secondo volume, del 1545, trattava di geometria e prospettiva. Due dei metodi di Serlio per costruire prospettive erano errati, ma ciò non impedì che la sua opera fosse ampiamente utilizzata. [23]

Progetto di Andrea Palladio e prospetto di Villa Pisani

Nel 1570, Andrea Palladio pubblicò, a Venezia, l'influente I quattro libri dell'architettura . Questo libro ampiamente stampato fu in gran parte motivo della diffusione delle idee del Rinascimento italiano in tutta Europa, assistito da sostenitori come il diplomatico inglese Henry Wotton con il suo The Elements of Architecture del 1624. [24] Le proporzioni di ogni stanza all'interno della villa erano calcolate su semplici rapporti matematici come 3: 4 e 4: 5, e le diverse stanze all'interno della casa correlate da questi rapporti. Precedenti architetti avevano usato queste formule per bilanciare un'unica facciata simmetrica; tuttavia, i disegni di Palladio riguardavano l'intera villa, generalmente quadrata. [25] Palladio consentì una serie di rapporti nei Quattro libri, affermando: [26] [27]

Nel 1615, Vincenzo Scamozzi pubblicò il trattato del tardo Rinascimento L'idea dell'architettura universale. [28] Tentò di mettere in relazione la progettazione di città ed edifici con le idee di Vitruvio e dei Pitagorici e con quelle più recenti di Palladio. [29]

XIX secolo

Faro reticolare iperboloide di Vladimir Shukhov, Ucraina, 1911

Le strutture iperboloidi furono utilizzate a partire dalla fine del XIX secolo da Vladimir Shukhov per alberi di imbarcazioni, fari e torri di raffreddamento. La loro forma sorprendente è sia esteticamente interessante che forte, utilizzando materiali strutturali economici. La prima torre iperboloidale di Shukhov fu esposta a Nizhny Novgorod nel 1896. [30] [31] [32]

XX secolo

I piani scorrevoli e intersecanti di De Stijl: la Rietveld Schröder House, 1924

Il movimento dei primi anni del XX secolo, l'architettura moderna, introdotta per la prima volta [N 3] dal costruttivismo russo, [33] usava la geometria euclidea rettilinea (detta anche cartesiana). Nel movimento De Stijl, l'orizzontale e il verticale erano visti come costituenti l'universale. La forma architettonica consiste nel mettere insieme queste due tendenze direzionali, usando piani del tetto, piani di pareti e balconi, che scivolano o si intersecano, come nella casa Rietveld Schröder del 1924 di Gerrit Rietveld. [34]

Raoul Heinrich Francé, papavero e porta pepe da tavola ( biomimetica ) da Die Pflanze als Erfinder, 1920

Gli architetti modernisti erano liberi di usare sia le curve che i piani. La stazione di Arnos del 1933 di Charles Holden ha una biglietteria circolare in mattoni con un tetto piano in cemento. Nel 1938, il pittore Bauhaus, Laszlo Moholy-Nagy, adottò i sette elementi biotecnologici di Raoul Heinrich Francé, vale a dire il cristallo, la sfera, il cono, il piano, la striscia (cuboidale), l'asta (cilindrica) e la spirale, come i presunti elementi di base dell'architettura ispirati alla natura. [35] [36]

Le Corbusier propose una scala antropometrica di proporzioni in architettura, il Modulor, basata sulla presunta altezza di un uomo. [37] La Chapelle Notre-Dame du Haut, del 1955, di Le Corbusier utilizza curve a forma libera non descrivibili con formule matematiche. [N 4] Si dice che le forme siano evocative di forme naturali come la prua di una nave o le mani in preghiera. [40] Il disegno è solo su larga scala: non esiste una gerarchia di dettagli su scale più piccole e quindi nessuna dimensione frattale; lo stesso vale per altri famosi edifici del XX secolo come il Sydney Opera House, l'aeroporto internazionale di Denver e il Guggenheim Museum di Bilbao. [38]

L'architettura contemporanea, secondo i 90 principali architetti che hanno risposto a un referendum sull'architettura, nel 2010, è estremamente diversificata; il migliore è stato giudicato il Museo Guggenheim di Frank Gehry, Bilbao. [41]

Le superfici minime del tetto in tessuto dell'aeroporto internazionale di Denver, completato nel 1995, evocano le montagne innevate del Colorado e le tende tepee dei nativi americani .

L'edificio del terminal dell'aeroporto internazionale di Denver, completato nel 1995, ha un tetto in tessuto supportato come una superficie minima (ovvero, la sua curvatura media è zero) da cavi d'acciaio. Evoca le montagne innevate del Colorado e le tende tepee dei nativi americani . [42] [43]

L'architetto Richard Buckminster Fuller è famoso per la progettazione di forti strutture a guscio sottile note come cupole geodetiche. La cupola del Montrosal Biosphère è alta 61 metri e il suo diametro è di 76 metri. [44]

Il Teatro dell'Opera di Sydney ha un tetto costituito da alte volte bianche, che ricordano le vele di una nave; per consentire di costruirli utilizzando componenti standardizzati, le volte sono tutte composte da sezioni triangolari di gusci sferici con lo stesso raggio. Questi hanno la curvatura uniforme richiesta in ogni direzione. [45]

Il decostruttivismo della fine del XX secolo crea deliberatamente disordine con ciò che Nikos Salingaros, in A Theory of Architecture, chiama forme casuali [46] di elevata complessità [47] usando pareti non parallele, griglie sovrapposte e complesse superfici 2D, come negli edifici di Frank Gehry, Disney Concert Hall e Guggenheim Museum, Bilbao. [48] [49] Fino al XX secolo, gli studenti di architettura erano obbligati a solide basi di matematica. Salingaros sostiene che prima il modernismo "eccessivamente semplicistico e guidato politicamente" e poi il decostruttivismo "anti-scientifico" hanno effettivamente separato l'architettura dalla matematica. Crede che questa "inversione di valori matematici" sia dannosa, in quanto l '"estetica pervasiva" dell'architettura non matematica addestra le persone "a rifiutare le informazioni matematiche nell'ambiente costruito"; sostiene che ciò ha effetti negativi sulla società. [38]

Principi religiosi

Antico Egitto

Base: ipotenuse (b: a) i rapporti per piramidi come la Grande Piramide di Giza potrebbero essere: 1: φ ( triangolo di Keplero ), 3: 5 ( triangolo 3: 4: 5 ) o 1: 4 / π

Le piramidi dell'antico Egitto sono tombe costruite con proporzioni matematiche, ma si è discusso quali fossero e se fosse stato usato il teorema di Pitagora. Il rapporto tra altezza inclinata e metà della lunghezza della base della Grande Piramide di Giza è inferiore dell'1% rispetto al rapporto aureo. Se questo fosse il metodo di progettazione, implicherebbe l'uso del triangolo di Keplero (angolo facciale 51° 49'), [50] [51] ma secondo molti storici della scienza, il rapporto aureo non era noto fino al tempo dei Pitagorici. [52] La Grande Piramide potrebbe anche essere stata basata su un triangolo con rapporto base / ipotenusa 1: 4 / π (angolo facciale 51° 50').

Le proporzioni di alcune piramidi potrebbero anche essere basate sul triangolo 3: 4: 5 (angolo frontale 53° 8'), noto dal Papiro matematico di Rhind (c. 1650-1550 a.C.); questo fu ipotizzato per la prima volta dallo storico Moritz Cantor nel 1882. [53] È noto che gli angoli retti erano disposti con precisione nell'antico Egitto usando corde annodate per la misurazione. Plutarco registrò, in Iside e Osiride (c. 100 ), che gli egiziani ammiravano il triangolo 3: 4: 5, e che una pergamena precedente al 1700 a.C. ha dimostrato formule quadrate di base. [54] [N 5] Lo storico Roger L. Cooke osserva che "È difficile immaginare che qualcuno potesse essere interessato a tali condizioni senza conoscere il teorema di Pitagora", ma osserva anche che nessun testo egiziano prima del 300 a.C. in realtà menziona l'uso del teorema per trovare la lunghezza dei lati di un triangolo e che ci sono modi più semplici per costruire un angolo retto. Cooke conclude che la congettura di Cantor rimane incerta; egli suppone che gli antichi egizi probabilmente conoscessero il teorema di Pitagora, ma "non ci sono prove che lo usassero per costruire gli angoli retti".

India antica

Gopuram del tempio indù Virupaksha ha una struttura simile a un frattale in cui le parti assomigliano al tutto.

Il Vaastu Shastra, l'antico canone indiano dell'architettura e dell'urbanistica, impiega disegni simmetrici chiamati mandala. Calcoli complessi vengono utilizzati per arrivare alle dimensioni di un edificio e dei suoi componenti. I progetti hanno lo scopo di integrare l'architettura con la natura, le funzioni relative di varie parti della struttura e antiche credenze che utilizzano modelli geometrici (yantra), simmetria e allineamenti direzionali. [55] [56] Tuttavia, i primi costruttori potrebbero aver scoperto proporzioni matematiche per caso. Il matematico Georges Ifrah nota che semplici trucchi con corde e pali possono essere utilizzati per disporre forme geometriche, come ellissi e angoli retti. [12] [57]

Pianta del tempio Meenakshi Amman, Madurai, dal VII secolo in poi. Le quattro porte (numerate I-IV) sono alti gopuram .

La matematica dei frattali è stata usata per dimostrare che il motivo per cui gli edifici esistenti hanno un fascino universale e sono visivamente soddisfacenti è perché forniscono allo spettatore un senso di scala a diverse distanze di visione. Ad esempio, negli alti cancelli in gopuram dei templi indù come il tempio Virupaksha ad Hampi costruito nel settimo secolo, e altri come il tempio Kandariya Mahadev a Khajuraho, le parti e il tutto hanno lo stesso carattere, con una dimensione frattale nell'intervallo da 1,7 a 1,8. L'ammasso di torri più piccole (shikhara, letteralmente "montagna") attorno alla torre più alta e centrale, che rappresenta il santo Monte Kailash, dimora del Signore Shiva, raffigura l'infinita ripetizione di universi nella cosmologia indù. [2] [58] L'esperto di studi religiosi William J. Jackson osservò il modello di torri raggruppate tra torri più piccole, esse stesse raggruppate tra torri ancora più piccole, che:

Il tempio Meenakshi Amman è un grande complesso con più santuari, con le strade di Madura disposte attorno ad esso in modo concentrico secondo gli shastra. Le quattro porte sono alte torri (gopuram) con struttura ripetitiva simile a un frattale come ad Hampi. I recinti attorno a ciascun santuario sono rettangolari e circondati da alti muri di pietra. [59]

Grecia antica

Il Partenone è stato progettato utilizzando rapporti di Pitagora.

Pitagora (ca. 569 - circa 475 a.C.) e i suoi seguaci, i Pitagorici, sostenevano che "tutte le cose sono numeri". Hanno osservato le armonie prodotte dalle note con specifici rapporti di piccolo numero intero e hanno sostenuto che anche gli edifici dovrebbero essere progettati con tali rapporti. La parola greca simmetria indicava originariamente l'armonia delle forme architettoniche in rapporti precisi, dai dettagli più piccoli di un edificio fino al suo intero disegno. [12]

Il Partenone è lungo 69,5 metri, largo 30,9 e alto 13, 7 al cornicione. Ciò fornisce un rapporto tra larghezza e lunghezza di 4: 9 e lo stesso tra altezza e larghezza. Mettendoli insieme si ottiene altezza: larghezza: lunghezza di 16:36:81, o per la gioia [60] dei Pitagorici 4 2 : 6 2 : 9 2 . Questo imposta il modulo su 0,858 metri. Un rettangolo 4: 9 può essere costruito come tre rettangoli contigui con lati nel rapporto 3: 4. Ogni mezzo rettangolo è quindi un comodo triangolo rettangolo 3: 4: 5, che consente di controllare angoli e lati con una corda opportunamente annodata. Anche l'area interna (naos) ha proporzioni 4: 9 ( 21,44 largo di 48.3 lungo); il rapporto tra il diametro delle colonne esterne, 1,905 metri (6,25 ft) e la distanza dei loro centri, 4,293 metri (14,08 ft) , è anche 4: 9. [12]

Pianta del Partenone

Il Partenone è considerato da autori come John Julius Norwich "il più perfetto tempio dorico mai costruito". Le sue elaborate raffinatezze architettoniche comprendono "una sottile corrispondenza tra la curvatura dello stilobato, la rastremazione delle pareti del naos e l' entasi delle colonne". [61] L'entasi si riferisce alla sottile diminuzione del diametro delle colonne mentre si alzano. Lo stilobato è la piattaforma su cui poggiano le colonne. Come in altri templi greci classici, [62] la piattaforma presenta una leggera curvatura parabolica verso l'alto per eliminare l'acqua piovana e rafforzare l'edificio contro i terremoti. Si potrebbe quindi supporre che le colonne si inclinino verso l'esterno, ma in realtà si inclinano leggermente verso l'interno in modo che se proseguissero, si incontrerebbero a circa un chilometro e mezzo sopra il centro dell'edificio; poiché hanno tutte la stessa altezza, la curvatura del bordo esterno dello stilobato viene trasmessa all'architrave e al tetto: "tutti seguono la regola di essere costruiti su curve delicate". [63]

Il rapporto aureo era noto nel 300 a.C., quando Euclide descrisse il metodo di costruzione geometrica. [64] È stato sostenuto che il rapporto aureo è stato utilizzato nella progettazione del Partenone e di altri antichi edifici greci, nonché di sculture, dipinti e vasi. [65] Autori più recenti come Nikos Salingaros, tuttavia, dubitano di tutte queste affermazioni. [66] Gli esperimenti dello scienziato informatico George Markowsky non sono riusciti a trovare alcuna preferenza per il rettangolo d'oro. [67]

Architettura islamica

Moschea Selimiye, Edirne, 1569-1575

Lo storico dell'arte islamica Antonio Fernandez-Puertas suggerisce che l' Alhambra, come la Grande Moschea di Cordova, [68] siano state progettate utilizzando il piede ispanico-musulmano o un gomito di circa 0,62 metri (2,0 ft) . Nella corte dei leoni del palazzo, le proporzioni seguono una serie di sorprese . Un rettangolo con i lati 1   e √ 2 ha (secondo il teorema di Pitagora ) una diagonale di √ 3, che descrive il triangolo rettangolo fatto dai lati della corte; la serie continua con √ 4 (dando un rapporto 1: 2), √ 5 e così via. I motivi decorativi sono proporzionati in modo simile, √ 2 generando quadrati all'interno dei cerchi e stelle a otto punte, √ 3 generando stelle a sei punte. Non ci sono prove a sostegno delle precedenti affermazioni secondo cui il rapporto aureo fosse stato usato nell'Alhambra. [10] [69] La Corte dei Leoni è racchiusa tra la Sala delle Due Sorelle e la Sala degli Abencerrajes; un esagono regolare può essere disegnato dai centri di queste due sale e dai quattro angoli interni della Corte dei Leoni. [70]

La moschea Selimiye di Edirne, in Turchia, è stata costruita da Mimar Sinan per fornire uno spazio in cui il mihrab potesse essere visto da qualsiasi parte all'interno dell'edificio. L'ampio spazio centrale è di conseguenza organizzato come un ottagono, formato da otto enormi pilastri e ricoperto da una cupola circolare di 31,25 metri (102,5 ft) diametro e alta 43 metri (141 ft) . L'ottagono è formato in un quadrato con quattro semidomi e esternamente da quattro minareti eccezionalmente alti, 83 metri (272 ft) . Il piano dell'edificio è quindi un cerchio, all'interno di un ottagono, all'interno di un quadrato. [71]

Architettura moghul

Il mausoleo del Taj Mahal con parte dei giardini del complesso ad Agra

L'architettura moghul, come si vede nella città imperiale abbandonata di Fatehpur Sikri e nel complesso Taj Mahal, ha un ordine matematico distintivo e un'estetica forte basata su simmetria e armonia. [11] [72]

Il Taj Mahal esemplifica l'architettura dei moghul, sia rappresentando il paradiso [73] sia mostrando il potere dell'imperatore Shah Jahan attraverso la sua scala, simmetria e costose decorazioni. Il mausoleo in marmo bianco, decorato con pietra dura, la grande porta ( Darwaza-i rauza ), altri edifici, i giardini e i percorsi formano insieme un disegno gerarchico unificato. Gli edifici includono una moschea in arenaria rossa a ovest e un edificio quasi identico, il Jawab o "risposta" a est per mantenere la simmetria bilaterale del complesso. Il charbagh formale ("quadruplo giardino") è diviso in quattro parti, che simboleggiano i quattro fiumi del paradiso e offrono vedute e riflessioni del mausoleo. Questi sono divisi a loro volta in 16 parterres. [74]

Planimetria del complesso del Taj Mahal . Il grande cancello è a destra, il mausoleo al centro, racchiuso tra la moschea (in basso) e il jawab. Il piano include quadrati e ottagoni .

Il complesso Taj Mahal è stato disposto su una griglia, suddivisa in griglie più piccole. Gli storici dell'architettura Koch e Barraud concordano con i resoconti tradizionali che danno la larghezza del complesso come 374 iarde o gaz Mughal, [N 6] l'area principale essendo tre quadrati di 374 gaz. Questi erano divisi in aree come il bazar e il caravanserraglio in moduli da 17 gaz; il giardino e le terrazze sono in moduli da 23 gaz e sono larghi 368 gaz (16 x 23). Il mausoleo, la moschea e la pensione sono disposti su una griglia di 7   gaz. Koch e Barraud osservano che se un ottagono, usato ripetutamente nel complesso, viene dato lati di 7   unità, quindi ha una larghezza di 17 unità, [N 7] che può aiutare a spiegare la scelta dei rapporti nel complesso. [75]

Architettura cristiana

La basilica patriarcale cristiana di Haghia Sophia a Bisanzio (oggi Istanbul ), costruita per la prima volta nel 537 (e ricostruita due volte), fu per mille anni [N 8] la più grande cattedrale mai costruita. Ha ispirato molti edifici successivi, tra cui quella di Sultan Ahmed e altre moschee della città. L' architettura bizantina comprende una navata coronata da una cupola circolare e due mezze cupole, tutte dello stesso diametro ( 31 metri (102 ft) ), con altre cinque mezze cupole più piccole che formano un'abside e quattro angoli arrotondati di un vasto interno rettangolare. [76] Ciò è stato interpretato dagli architetti medievali come rappresentante il mondano sotto (la base quadrata) e il cielo divino sopra (la cupola sferica impennata). [77] L'imperatore Giustiniano usò due geometri, Isidoro di Mileto e Anthemius di Tralles come architetti; Isidoro compilò le opere di Archimede sulla geometria solida e fu influenzato da lui. [12] [78]

Haghia Sophia, Istanbul



a) Piano della galleria (metà superiore)



b) Pianta del piano terra (metà inferiore)

L'importanza del battesimo in acqua nel cristianesimo si rifletteva nella scala dell'architettura battesimale. Il più antico, il Battistero lateranense di Roma, costruito nel 440, [79] creò una tendenza per i fonti battesimali ottagonali; il fonte battesimale all'interno di questi edifici era spesso ottagonale, sebbene il più grande battistero italiano, a Pisa, costruito tra il 1152 e il 1363, sia circolare, con un fonte ottagonale. Si tratta di 54,86 metri (180,0 ft) alto, con un diametro di 34,13 metri (112,0 ft) (un rapporto di 8: 5). [80] Sant'Ambrogio scrisse che i fonti e i battisteri erano ottagonali "perché l'ottavo giorno, [N 9] in aumento, Cristo scioglie la schiavitù della morte e riceve i morti dalle loro tombe". [81] [82] Anche Sant'Agostino descrisse l'ottavo giorno come "eterno   ... santificato dalla risurrezione di Cristo ". [83] Il Battistero ottagonale di San Giovanni, Firenze, costruito tra il 1059 e il 1128, è uno degli edifici più antichi di quella città e uno degli ultimi nella tradizione diretta dell'antichità classica; fu estremamente influente nel successivo Rinascimento fiorentino, poiché importanti architetti tra cui Francesco Talenti, Alberti e Brunelleschi lo usarono come modello di architettura classica. [84]

Il numero cinque è usato "esuberantemente" [85] nella chiesa di pellegrinaggio del 1721 di San Giovanni Nepomuceno a Zelená hora, vicino a Žďár nad Sázavou nella repubblica ceca, progettata da Jan Blažej Santini Aichel . La navata è circolare, circondata da cinque coppie di colonne e cinque cupole ovali alternate ad absidi ogivali. La chiesa ha inoltre cinque porte, cinque cappelle, cinque altari e cinque stelle; una leggenda afferma che quando San Giovanni Nepomuceno fu martirizzato, cinque stelle apparvero sopra la sua testa. [86] L'architettura a cinque può anche simboleggiare le cinque ferite di Cristo e le cinque lettere di "Tacui" (latino: "Ho mantenuto il silenzio" [sui segreti del confessionale ]). [87]

Antoni Gaudí ha utilizzato un'ampia varietà di strutture geometriche, alcune delle quali minimali, nella Sagrada Família di Barcellona, iniziata nel 1882 (e non ancora completata nel 2020). Queste includono paraboloidi iperbolici e iperboloidi della rivoluzione, [88] tassellazioni, archi di catenaria, catenoidi, elicoidi e superfici rigate . Questo variegato mix di geometrie si combina creativamente in diversi modi intorno alla chiesa. Ad esempio, nella facciata della Passione della Sagrada Família, Gaudí riuniva "rami" di pietra sotto forma di paraboloidi iperbolici, che si sovrappongono in cima (direttrici) senza quindi incontrarsi in un punto. Al contrario, nel colonnato ci sono superfici paraboliche iperboliche che si uniscono in modo uniforme ad altre strutture per formare superfici illimitate. Inoltre, Gaudí sfrutta schemi naturali, essi stessi matematici, con colonne derivate dalle forme degli alberi e architravi realizzate con basalto non modificato e naturalmente fessurato (raffreddandosi dalla roccia fusa) in colonne esagonali . [89] [90] [91]

La Cattedrale di Santa Maria Assunta del 1971 , a San Francisco, ha un tetto a due falde composto da otto segmenti di paraboloidi iperbolici, disposti in modo che la sezione trasversale orizzontale inferiore del tetto sia quadrata e la sezione trasversale superiore una croce cristiana . L'edificio è un quadrato 77,7 metri (255 ft) su un lato e 57,9 metri (190 ft) alto. [92] La Cattedrale di Brasilia del 1970 di Oscar Niemeyer fa un uso diverso di una struttura iperboloide; è costruito da 16 identiche travi di cemento, ciascuna del peso di 90 tonnellate, [N 10] disposte in un cerchio per formare un iperboloide di rivoluzione, i raggi bianchi che creano una forma simile a mani che pregano il cielo. Dall'esterno è visibile solo la cupola: la maggior parte dell'edificio è sotto terra. [93] [94] [95] [96]

Diverse chiese medievali in Scandinavia sono circolari, di cui quattro sull'isola danese di Bornholm . Una delle più antiche di queste, la chiesa di Østerlars del c. 1160, ha una navata circolare attorno a una massiccia colonna circolare in pietra, trafitta da archi e decorata con un affresco. La struttura circolare ha tre piani ed era apparentemente fortificata, il piano superiore serviva per la difesa. [97] [98]

Decorazione matematica

Decorazione architettonica islamica

Gli edifici islamici sono spesso decorati con motivi geometrici che tipicamente fanno uso di diverse tessellazioni matematiche, formate da piastrelle di ceramica ( girih, zellige ) che possono essere esse stesse semplici o decorate con strisce. [12] Simmetrie come stelle con sei, otto o multipli di otto punti sono usate nei modelli islamici. Alcuni di questi sono basati sul motivo del sigillo "Khatem Sulemani" o Salomone, che è una stella a otto punte composta da due quadrati, uno ruotato di 45 gradi rispetto allo stesso centro. [99] I modelli islamici sfruttano molti dei 17 possibili gruppi di carte da parati ; già nel 1944, Edith Müller dimostrò che l'Alhambra faceva uso di 11 gruppi di carte da parati nelle sue decorazioni, mentre nel 1986 Branko Grünbaum affermò di aver trovato 13 gruppi di carte da parati nell'Alhambra, affermando controverse che i restanti quattro gruppi non si trovano da nessuna parte nell'ornamento dellIslam.

Decorazione architettonica moderna

Verso la fine del XX secolo, gli architetti hanno realizzato nuovi costrutti matematici come la geometria frattale e la piastrellatura aperiodica per fornire interessanti e attraenti coperture per gli edifici. [4] Nel 1913, l'architetto modernista Adolf Loos aveva dichiarato che "L'ornamento è un crimine", [100] influenzando il pensiero architettonico per il resto del XX secolo. Nel XXI secolo, gli architetti stanno nuovamente iniziando a esplorare l'uso dell'ornamento che è estremamente vario. A Reykjavik, il centro conferenze e concerti Harpa di Henning Larsen del 2011, ha quello che sembra una parete di cristallo di roccia fatta di grandi blocchi di vetro. Il Ravensbourne College 2010 di Londra, è decorato a mosaico con 28.000 piastrelle di alluminio anodizzato in rosso, bianco e marrone, che collegano finestre circolari di diverse dimensioni. La tassellatura utilizza tre tipi di tessera, un triangolo equilatero e due pentagoni irregolari. [101] [N 11] La biblioteca Kanazawa Umimirai di Kazumi Kudo crea una griglia decorativa fatta di piccoli blocchi circolari di vetro incastonati in semplici pareti di cemento.

Difesa

Europa

L'architettura delle fortificazioni si è evoluta dalle fortezze medievali, che avevano alte difese in muratura, a forti a stella simmetrici in grado di resistere ai bombardamenti di artiglieria tra la metà del XV e il XIX secolo. La geometria delle forme delle stella era dettata dalla necessità di evitare zone morte in cui la fanteria attaccante poteva ripararsi dal fuoco difensivo; i lati dei punti sporgenti erano angolati per consentire a tale fuoco di spazzare il terreno e fornire fuoco incrociato (da entrambi i lati) oltre ogni punto sporgente. Famosi architetti che progettarono tali difese includono Michelangelo, Baldassare Peruzzi, Vincenzo Scamozzi e Sébastien Le Prestre de Vauban . [103] [104]

Lo storico dell'architettura Siegfried Giedion sostenne che la fortificazione a forma di stella ebbe un'influenza formativa sulla struttura della città ideale del Rinascimento: "Il Rinascimento fu ipnotizzato da un tipo di città che per un secolo e mezzo - da Filarete a Scamozzi - fu scolpita in tutti gli schemi utopici: questa è la città a forma di stella ". [105]

Cina

Un tulou nella contea di Yongding, provincia del Fujian

Nell'architettura cinese, i tulou della provincia del Fujian sono strutture difensive circolari comuni con pareti prevalentemente bianche e un'unica porta di legno rivestita di ferro, alcune risalenti al XVI secolo. Le pareti sono sormontate da tetti che si inclinano dolcemente verso l'esterno e verso l'interno, formando un anello. Il centro del cerchio è un cortile acciottolato aperto, spesso con un pozzo, circondato da gallerie a graticcio alte fino a cinque piani.

Obiettivi ambientali

Yakhchal a Yazd, Iran

Gli architetti possono anche selezionare la forma di un edificio per soddisfare gli obiettivi ambientali. [85] Ad esempio, la 30 St Mary Axe di Londra, Foster and Partners, conosciuta come " The Gherkin " per la sua forma simile a un cetriolo, è un solido di rivoluzione progettato usando la modellazione parametrica . La sua geometria è stata scelta non solo per motivi estetici, ma per ridurre al minimo le correnti d'aria vorticose alla base. Nonostante la superficie apparentemente curva dell'edificio, tutti i pannelli di vetro che formano la sua superficie sono piatti, ad eccezione della lente nella parte superiore. La maggior parte dei pannelli sono quadrilateri, in quanto possono essere tagliati da vetro rettangolare con meno sprechi rispetto ai pannelli triangolari. [1]

Il tradizionale yakhchal (buca di ghiaccio) della Persia funzionava come un dispositivo di raffreddamento per evaporazione . Sopra la superficie, la struttura aveva una forma a cupola, ma aveva uno spazio sotterraneo per il ghiaccio e talvolta anche per il cibo. Lo spazio sotterraneo e la spessa costruzione resistente al calore isolavano tutto l'anno lo spazio di stoccaggio. Lo spazio interno veniva spesso ulteriormente raffreddato con i windcatcher. Il ghiaccio era disponibile in estate per rconservare il faloodeh, dessert congelato. [106]

Note

  1. ^ In Book 4, chapter 3 of De architectura, he discusses modules directly.[15]
  2. ^ A Roman foot was about 0,296 metri (0,97 ft).
  3. ^ Constructivism influenced Bauhaus and Le Corbusier, for example.[33]
  4. ^ Pace Nikos Salingaros, who suggests the contrary,[38] but it is not clear exactly what mathematics may be embodied in the curves of Le Corbusier's chapel.[39]
  5. ^ Berlin Papyrus 6619 from the Middle Kingdom stated that "the area of a square of 100 is equal to that of two smaller squares. The side of one is ½ + ¼ the side of the other."
  6. ^ 1 gaz is about 0,86 metri (2,8 ft).
  7. ^ A square drawn around the octagon by prolonging alternate sides adds four right angle triangles with hypotenuse of 7 and the other two sides of Template:Radic or 4.9497..., nearly 5. The side of the square is thus 5+7+5, which is 17.
  8. ^ Until Seville Cathedral was completed in 1520.
  9. ^ The sixth day of Holy Week was Good Friday; the following Sunday (of the resurrection) was thus the eighth day.[81]
  10. ^ This is 90 tonnellate (89 long ton; 99 short ton).
  11. ^ An aperiodic tiling was considered, to avoid the rhythm of a structural grid, but in practice a Penrose tiling was too complex, so a grid of 2.625m horizontally and 4.55m vertically was chosen.[102]
  1. ^ a b c Marianne Freiberger, plus.maths.org, Plus magazine, 1º March 2007, https://plus.maths.org/content/perfect-buildings-maths-modern-architecture. URL consultato il 5 October 2015.
  2. ^ a b Iasef Md Rian, Jin-Ho Park e Hyung Uk Ahn, Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho, in Building and Environment, vol. 42, 2007, pp. 4093–4107, DOI:10.1016/j.buildenv.2007.01.028.
  3. ^ Williams, Kim (a cura di), Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s, Birkhäuser, 2015, pp. chapter 1. 1–24, ISBN 978-3-319-00136-4.
  4. ^ a b Williams, Kim (a cura di), Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future, Birkhäuser, 2015, pp. chapter 48. 1–24, ISBN 978-3-319-00142-5.
  5. ^ careercornerstone.org, Sloan Career Cornerstone Center, https://web.archive.org/web/20150714164847/http://www.careercornerstone.org/pdf/archeng/archeng.pdf. URL consultato l'11 October 2015 (archiviato dall'url originale il 14 July 2015).
  6. ^ Michael Leyton, A Generative Theory of Shape, Springer, 2001, ISBN 978-3-540-42717-9.
  7. ^ Alexey Stakhov e Olsen Olsen, The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science, World Scientific, 2009, ISBN 978-981-277-582-5.
  8. ^ William Smith, Dictionary of Greek and Roman Biography and Mythology, Little, Brown, 1870, p. 620.
  9. ^ a b Vitruvius, On Architecture, Penguin Books, 2009, pp. 8–9, ISBN 978-0-14-193195-1.
  10. ^ a b Raymond Tennant, International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen. (PDF), in International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science, July 2003.
  11. ^ a b Jaswant Rai, Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri, in Journal of King Saud University, Architecture & Planning, vol. 5, n. 1, 1993, pp. 19–48.[collegamento interrotto] Errore nelle note: Tag <ref> non valido; il nome "Rai" è stato definito più volte con contenuti diversi
  12. ^ a b c d e f g J. J. O'Connor e Robertson, www-history.mcs.st-and.ac.uk, University of St Andrews, February 2002, http://www-history.mcs.st-and.ac.uk/HistTopics/Architecture.html. URL consultato il 4 October 2015.
  13. ^ Saskia van den Hoeven e van der Veen, jphogendijk.nl, Utrecht University, 2010, https://web.archive.org/web/20160304040643/http://www.jphogendijk.nl/projects/muqarnas2010.pdf. URL consultato il 30 September 2015 (archiviato dall'url originale il 4 March 2016).
  14. ^ Felipe Cucker, Manifold Mirrors: The Crossing Paths of the Arts and Mathematics, Cambridge University Press, 2013, pp. 103–106, ISBN 978-0-521-72876-8.
  15. ^ VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order, su vitruvius.be. URL consultato il 6 October 2015.
  16. ^ Kim Williams e Michael J. Ostwald, Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s, Birkhäuser, 9 February 2015, pp. 42, 48, ISBN 978-3-319-00137-1.
  17. ^ Leland M. Roth, Understanding Architecture: Its Elements, History, And Meaning, Boulder, Westview Press, 1992, p. 36, ISBN 0-06-438493-4.
  18. ^ Amanda Claridge, Rome, collana Oxford Archaeological Guides, Oxford Oxfordshire, Oxford University Press, 1998, pp. 204–5, ISBN 0-19-288003-9.
  19. ^ Lynne C. Lancaster, Concrete Vaulted Construction in Imperial Rome: Innovations in Context, Cambridge, Cambridge University Press, 2005, pp. 44–46, ISBN 0-521-84202-6.
  20. ^ Lionel March, Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria, in Architectural Research Quarterly, vol. 2, n. 1, 1996, pp. 54–65, DOI:10.1017/S135913550000110X.
  21. ^ Mathalino.com Engineering Math Review, http://www.mathalino.com/reviewer/solid-mensuration-solid-geometry/013-insciribed-and-circumscribed-sphere-about-cube-volume-. URL consultato il 4 October 2015.
  22. ^ Typ 525.69.781, Houghton Library, Harvard University
  23. ^ Kirsti Andersen, The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge, Springer, 2008, pp. 117–121, ISBN 978-0-387-48946-9.
  24. ^ Carsten Ruhl, ieg-ego.eu, European History Online, 7 April 2011, http://ieg-ego.eu/en/threads/europe-on-the-road/educational-journey-grand-tour/carsten-ruhl-palladianism. URL consultato il 3 October 2015.
  25. ^ Copplestone, Trewin, World Architecture, Hamlyn, 1963, p. 251.
  26. ^ Stephen R. Wassell, emis.de, Nexus Network Journal, http://www.emis.de/journals/NNJ/Wassell.html. URL consultato il 3 October 2015.
  27. ^ Palladio, Andrea e Tavernor, Robert; Schofield, Richard (trans.), I quattro libri dell'architettura, MIT Press, 1997 [1570], p. book I, chapter xxi, page 57.
  28. ^ Scamozzi, Vincenzo e Vroom, W. H. M. (trans.), The Idea of a Universal Architecture, Architectura & Natura, 2003 [1615].
  29. ^ Ann Marie Borys, Vincenzo Scamozzi and the Chorography of Early Modern Architecture, Ashgate Publishing, 28 March 2014, pp. 140–148 and passim, ISBN 978-1-4094-5580-6.
  30. ^ Matthias Beckh, Hyperbolic Structures: Shukhov's Lattice Towers – Forerunners of Modern Lightweight Construction, John Wiley & Sons, 2015, pp. 75 and passim, ISBN 978-1-118-93268-1.
  31. ^ The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span, in The Engineer, 19 March 1897, pp. 292–294.
  32. ^ Graefe, Rainer, Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion, Deutsche Verlags-Anstalt, 1990, pp. 110–114, ISBN 3-421-02984-9.
  33. ^ a b Owen Hatherley, The Constructivists and the Russian Revolution in Art and Architecture, 4 November 2011. URL consultato il 6 June 2016.
  34. ^ World Heritage Centre, UNESCO, https://whc.unesco.org/en/list/965. URL consultato il 13 December 2012.
  35. ^ Laszlo Moholy-Nagy e Daphne M. (trans.) Hoffman, The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture, New Bauhaus Books, 1938, p. 46.
  36. ^ Lynn Gamwell, Mathematics and Art: A Cultural History, Princeton University Press, 2015, p. 306, ISBN 978-0-691-16528-8.
  37. ^ Le Corbusier, The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics, Birkhäuser, 2004 [1954 and 1958], ISBN 3-7643-6188-3.
  38. ^ a b c Nikos Salingaros, emis.de, Nexus Network Journal, http://www.emis.de/journals/NNJ/Salingaros.html. URL consultato il 9 October 2015. Updated version of Nikos Salingaros, Architecture, Patterns, and Mathematics, in Nexus Network Journal, vol. 1, n. 2, April 1999.
  39. ^ Le Corbusier: Notre Dame du Haut at Ronchamp, su herbgreene.org. URL consultato il 5 October 2015.[collegamento interrotto]
  40. ^ David A. Hanser, Architecture of France, Greenwood Publishing Group, 2006, p. 211, ISBN 978-0-313-31902-0.
  41. ^ Vanity Fair's World Architecture Survey: the Complete Results, in Vanity Fair, 30 June 2010. URL consultato il 22 July 2010.
  42. ^ business.flydenver.com, Denver International Airport, 2014, https://web.archive.org/web/20150412011439/http://business.flydenver.com/info/news/pressKit.pdf. URL consultato il 5 October 2015 (archiviato dall'url originale il 12 April 2015).
  43. ^ architonic.com, Fenstress Architects, http://www.architonic.com/aisht/denver-international-airport-fentress-architects/5100647. URL consultato il 5 October 2015.
  44. ^ A view on cities, http://www.aviewoncities.com/montreal/biosphere.htm. URL consultato il 1º October 2015.
  45. ^ Alexander J. Hahn, insidescience.org, Inside Science, 4 February 2013, https://www.insidescience.org/content/mathematical-excursions-architecture/927. URL consultato il 5 October 2015.
  46. ^ Salingaros, Nikos, A Theory of Architecture, Umbau, 2006, pp. 139–141.
  47. ^ Salingaros, Nikos, A Theory of Architecture, Umbau, 2006, pp. 124–125.
  48. ^ Gehry, Frank O., Mudford, Grant e Koshalek, Richard, Symphony: Frank Gehry's Walt Disney Concert Hall, Five Ties, 2009.
  49. ^ Garcetti, Gil, Iron: Erecting the Walt Disney Concert Hall, Princeton Architectural Press, 2004.
  50. ^ Christopher Bartlett, The Design of The Great Pyramid of Khufu, in Nexus Network Journal, vol. 16, n. 2, 2014, pp. 299–311, DOI:10.1007/s00004-014-0193-9.
  51. ^ Markowsky, George, Misconceptions About the Golden Ratio (PDF), in The College Mathematics Journal, vol. 23, n. 1, January 1992. URL consultato il 1º ottobre 2015 (archiviato dall'url originale l'8 aprile 2008).
  52. ^ Mario Livio, The Golden Ratio: The Story of Phi, the World's Most Astonishing Number, First trade paperbackª ed., New York City, Broadway Books, 2003 [2002], p. 61, ISBN 0-7679-0816-3.
  53. ^ Roger L. Cooke, The History of Mathematics: A Brief Course, 2ndª ed., John Wiley & Sons, 2011, pp. 237–238, ISBN 978-1-118-03024-0.
  54. ^ Gillings, Richard J., Mathematics in the Time of the Pharaohs, Dover, 1982, p. 161.
  55. ^ Kramrisch, Stella (1976), The Hindu Temple Volume 1 & 2, ISBN 81-208-0223-3
  56. ^ Vibhuti Sachdev, Giles Tillotson, Building Jaipur: The Making of an Indian City, 2004, pp. 155–160, ISBN 978-1-86189-137-2.
  57. ^ Ifrah, Georges, A Universal History of Numbers, Penguin, 1998.
  58. ^ classes.yale.edu, Yale University, https://web.archive.org/web/20120206011944/http://classes.yale.edu/Fractals/Panorama/Architecture/IndianArch/IndianArch.html. URL consultato il 1º October 2015 (archiviato dall'url originale il 6 February 2012).
  59. ^ Anthony D. King, Buildings and Society: Essays on the Social Development of the Built Environment, Taylor & Francis, 2005, p. 72, ISBN 0-203-48075-9.
  60. ^ Eli Maor, The Pythagorean Theorem: A 4,000-year History, Princeton University Press, 2007, p. 19, ISBN 0-691-12526-0.
  61. ^ Norwich, John Julius, Great Architecture of the World, Artists House, 2001, p. 63.
  62. ^ Penrose, Francis, Principles of Athenian Architecture, Society of Dilettanti, 1973 [1851], p. ch. II.3, plate 9.
  63. ^ Stevens, Gorham P., Concerning the Impressiveness of the Parthenon, in American Journal of Archaeology, vol. 66, n. 3, July 1962, pp. 337–338, DOI:10.2307/501468.
  64. ^ Euclid. Elements. Book 6, Proposition 30.
  65. ^ Archibald, R. C., spirasolaris.ca, http://www.spirasolaris.ca/hambidge1a.html. URL consultato il 1º October 2015.
  66. ^ Applications of the Golden Mean to Architecture
  67. ^ Markowsky, George, Misconceptions about the Golden Ratio (PDF), in The College Mathematics Journal, vol. 23, n. 1, January 1992. URL consultato il 1º ottobre 2015 (archiviato dall'url originale l'8 aprile 2008).
  68. ^ Najib Gedal, islamic-arts.org, Islamic Art & Architecture, https://web.archive.org/web/20151002022611/http://islamic-arts.org/2011/the-great-mosque-of-cordoba-geometric-analysis/. URL consultato il 16 October 2015 (archiviato dall'url originale il 2 October 2015).
  69. ^ Robert Irwin, The Alhambra, Profile Books, 26 May 2011, pp. 109–112, ISBN 1-84765-098-8.
  70. ^ Ann Robertson, archive.bridgesmathart.org, BRIDGES, 2007, http://archive.bridgesmathart.org/2007/bridges2007-303.pdf. URL consultato l'11 October 2015.
  71. ^ Sheila Blair e Jonathan M. Bloom, The Art and Architecture of Islam 1250–1800, Yale University Press, 1995, ISBN 0-300-06465-9.
  72. ^ George Michell e Amit Pasricha, Mughal Architecture & Gardens, Antique Collectors Club, 2011, ISBN 978-1-85149-670-9.
  73. ^ Philip Parker, World History, Dorling Kindersley, 2010, p. 224, ISBN 978-1-4053-4124-0.
  74. ^ Ebba Koch, The Complete Taj Mahal: And the Riverfront Gardens of Agra, 1stª ed., Thames & Hudson, 2006, pp. 24 and passim, ISBN 0-500-34209-1.
  75. ^ Ebba Koch, The Complete Taj Mahal: And the Riverfront Gardens of Agra, 1stª ed., Thames & Hudson, 2006, pp. 104–109, ISBN 0-500-34209-1.
  76. ^ Michael Fazio, Marian Moffett e Lawrence Wodehouse, Buildings Across Time, 3rdª ed., McGraw-Hill Higher Education, 2009, ISBN 978-0-07-305304-2.
  77. ^ Lynn Gamwell, Mathematics and Art: A Cultural History, Princeton University Press, 2015, p. 48, ISBN 978-0-691-16528-8.
  78. ^ Fred S. Kleiner e Mamiya, Christin J., Gardner's Art Through the Ages: Volume I, Chapters 1–18, 12thª ed., Wadsworth, 2008, p. 329, ISBN 0-495-46740-5.
  79. ^ Hanna Menander, Brandt, Appetechia e Thorén, samla.raa.se, Swedish National Heritage Board, 2010, http://samla.raa.se/xmlui/bitstream/handle/raa/5009/ro2010_18.pdf. URL consultato il 30 October 2015.
  80. ^ The Leaning Tower of Pisa, http://www.leaningtowerofpisa.net/pisa-baptistery.html. URL consultato il 30 October 2015.
  81. ^ a b Joan Huyser-Konig, worship.calvin.edu, Calvin Institute of Christian Worship, http://worship.calvin.edu/resources/resource-library/theological-reasons-for-baptistry-shapes/. URL consultato il 30 October 2015.
  82. ^ Regina Kuehn, A Place for Baptism, Liturgy Training Publications, 1992, pp. 53–60, ISBN 978-0-929650-00-5.
  83. ^ Augustine of Hippo, The City of God, 426, p. Book 22, Chapter 30.
  84. ^ Fred Kleiner, Gardner's Art through the Ages: A Global History, Cengage Learning, 2012, pp. 355–356, ISBN 1-133-71116-2.
  85. ^ a b Andrea Simitch e Val Warke, The Language of Architecture: 26 Principles Every Architect Should Know, Rockport Publishers, 2014, p. 191, ISBN 978-1-62788-048-0.
  86. ^ czechtourism.com, Czech Tourism, http://www.czechtourism.com/c/zdar-nad-sazavou-unesco-zelena-hora-pilgrimage-church-of-st-john-nepomuk/. URL consultato il 10 November 2015.
  87. ^ Saint John of Nepomuk, https://web.archive.org/web/20160304064831/http://www.sjn.cz/eng/attributes.htm. URL consultato il 10 November 2015 (archiviato dall'url originale il 4 March 2016).
  88. ^ M.C., J.R. Burry, G.M. Dunlop and A. Maher Burry, Presented at SIRC 2001 – the Thirteenth Annual Colloquium of the Spatial Information Research Center, University of Otago, 2001, https://web.archive.org/web/20071031134218/http://www.business.otago.ac.nz/SIRC05/conferences/2001/05_burry.pdf. URL consultato il 28 novembre 2007 (archiviato dall'url originale il 31 ottobre 2007).
  89. ^ Math & the Art of MC Escher, Saint Louis University Mathematics and Computer Science, http://euler.slu.edu/escher/index.php/The_Geometry_of_Antoni_Gaudi. URL consultato il 4 October 2015.
  90. ^ Liliana Usvat, mathematicsmagazine.com, Mathematics Magazine, http://www.mathematicsmagazine.com/Articles/AntonyGaudiandMathematics.php#.VhFZ7WtUWHg. URL consultato il 4 October 2015.
  91. ^ M.C. Burry, J.R. Burry e G.M. Dunlop, Drawing Together Euclidean and Topological Threads (PDF), The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand, 2001. URL consultato il 5 August 2008 (archiviato dall'url originale il 25 June 2008).
  92. ^ Pier Luigi Nervi, Architectuul, http://architectuul.com/architecture/cathedral-of-saint-mary-of-the-assumption. URL consultato il 12 October 2015.
  93. ^ aboutbrasilia.com, About Brasilia, http://www.aboutbrasilia.com/travel/brasilia-cathedral.html. URL consultato il 13 November 2015.
  94. ^ Ehrhard Behrends, Nuno Crato e Jose Francisco Rodrigues, Raising Public Awareness of Mathematics, Springer Science & Business Media, 2012, p. 143, ISBN 978-3-642-25710-0.
  95. ^ Michele Emmer, Imagine Math: Between Culture and Mathematics, Springer Science & Business Media, 2012, p. 111, ISBN 978-88-470-2427-4.
  96. ^ Ruzanna Mkrtchyan, building.am, 2013, http://www.building.am/page.php?id=149. URL consultato il 13 November 2015.
  97. ^ (Danish) nordenskirker.dk, Nordens kirker, http://www.nordenskirker.dk/Tidligere/oesterlars_kirke/oesterlars_kirke.htm. URL consultato il 2 December 2016. Lingua sconosciuta: Danish (aiuto)
  98. ^ (Danish) naturbornholm.dk, Natur Bornholm, https://web.archive.org/web/20110719142238/http://www.naturbornholm.dk/default.asp?m=373. URL consultato il 2 December 2016 (archiviato dall'url originale il 19 July 2011). Lingua sconosciuta: Danish (aiuto)
  99. ^ Rønning, Frode, people.exeter.ac.uk, University of Exeter, http://people.exeter.ac.uk/PErnest/pome24/ronning%20_geometry_and_Islamic_patterns.pdf. URL consultato il 18 April 2014.
  100. ^ Matt Gibberd e Albert Hill, The Return of Ornamentation, in The Telegraph, 20 August 2013. URL consultato il 12 October 2015.
  101. ^ dezeen.com, de zeen magazine, 13 September 2010, http://www.dezeen.com/2010/09/13/ravensbourne-college-by-foreign-office-architects/. URL consultato il 12 October 2015.
  102. ^ FOA's peninsula patterns for Ravensbourne College, su bdonline.co.uk. URL consultato il 16 October 2015.
  103. ^ Duffy, C., Fire & Stone, The Science of Fortress Warfare 1660–1860, Booksales, 1975, ISBN 978-0-7858-2109-0.
  104. ^ David Chandler, The Art of Warfare in the Age of Marlborough, Spellmount, 1990, ISBN 978-0-946771-42-4.
  105. ^ Giedion, Siegfried, Space, Time and Architecture, Harvard University Press, 1962 [1941], p. 43.
  106. ^ M. Mahdavinejad e Javanrudi, Kavan, Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates, in Asian Culture and History, vol. 4, n. 2, July 2012, DOI:10.5539/ach.v4n2p133.

Collegamenti esterni

[[Categoria:Teoria dell'architettura]] [[Categoria:Pagine con traduzioni non revisionate]]

Estratto da "https://it.wikipedia.org/w/index.php?title=Matematica_e_architettura&oldid=114053222"