Rettangolo aureo
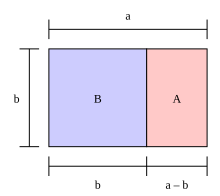
Il rettangolo aureo è un rettangolo le cui proporzioni sono basate sulla proporzione aurea. Ciò significa che il rapporto fra il lato maggiore e quello minore, a : b, è identico a quello fra il lato minore e il segmento ottenuto sottraendo quest'ultimo dal lato maggiore b : a−b (il che implica che entrambi i rapporti siano 1,618).
La particolarità saliente è la sua facile replicabilità: difatti, basta disegnarvi all'interno un quadrato basato sul lato minore, o altresì, all'esterno, basato sul lato maggiore, sì da ottenere col semplice compasso un altro rettangolo, minore o maggiore, anch'esso di proporzioni auree.
Le sue particolarità, nonché l'alone che già risiedeva attorno alla proporzione aurea, sulla quale è basato, l'hanno fatto considerare nei secoli un canone di bellezza assoluto; non sono mancate nell'800 persino indagini psicologiche volte ad avvalorare tale tesi, e nonostante successive verifiche l'abbiano del tutto privata di valore scientifico ancora oggi è diffusa l'idea che il rettangolo aureo sia il "rettangolo più bello".
Costruzioni e approssimazioni geometriche[modifica | modifica wikitesto]
Costruzione con riga e compasso[modifica | modifica wikitesto]
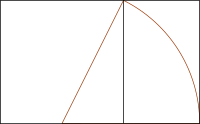
Il procedimento di costruzione del rettangolo aureo con il solo ausilio di riga e compasso è stato presentato per la prima volta da Euclide nella proposizione 2.11 degli elementi.
Si costruisce dapprima un quadrato, il cui lato corrisponderà al lato minore del rettangolo. Si trova poi il punto medio di un lato e si punta su di esso un compasso con apertura sino a un vertice non adiacente del quadrato. Il punto nel quale la circonferenza così determinata interseca il prolungamento del lato determina il secondo estremo del lato maggiore del rettangolo.
La dimostrazione è veloce:

Considerando 1 il lato del quadrato, l'apertura del compasso che punta nel punto medio risulta, applicando il teorema di Pitagora:
- .
Considerando che il segmento di tale lunghezza va aggiunto ad una porzione pari a ½ del lato, il lato maggiore costruito misurerà complessivamente:
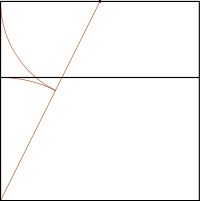
Il rettangolo aureo può essere ricavato anche all'interno del perimetro del quadrato, con un metodo che ricalca quello usato per dividere un segmento in proporzione aurea:
- Si traccia una diagonale da un vertice a uno dei punti medi dei lati.
- Si riporta sulla diagonale una lunghezza uguale a ½ lato del quadrato.
- La lunghezza restante la si riporta su un lato, completando poi il rettangolo.
Il rettangolo di maggiori dimensioni così ottenuto è un rettangolo aureo, che sta in proporzione 1/φ al quadrato iniziale, mentre il più piccolo ricavato è uguale alla somma di tutti i rettangoli aurei ricavabili all'interno del principale (vedi oltre).
Calcolo algebrico del rapporto[modifica | modifica wikitesto]
Considerando sempre 1 il lato maggiore (a), in comune col quadrato il lato minore, per quanto nella figura e nel testo in prefazione, ha misura:
- a questo risultato si perviene risolvendo l'equazione di secondo grado b2+b-1=0.
Costruzione attraverso piegature di un foglio[modifica | modifica wikitesto]
Esiste un modo elegante per ottenere un rettangolo aureo da un rettangolo qualsiasi, attraverso successive piegature di un foglio di carta.
Come mostrato da Corrado Falcolini, il numero di piegature richieste è in questo caso pari solo a 3[1]. Il rettangolo aureo ottenuto ha per lato maggiore lo stesso della figura originaria mentre il lato minore è ottenuto accorciando quello originario[1].
Approssimazione mediante la successione di Fibonacci[modifica | modifica wikitesto]
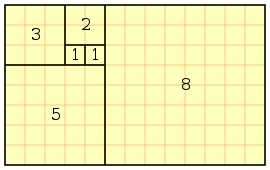
Un modo alternativo per costruire un rettangolo dalle proporzioni auree è quello di accostare in successione quadrati che abbiano per lati i valori della successione di Fibonacci: 1, 1, 2, 3, 5, 8...
In questo modo si creerà una successione di rettangoli sempre più vicini a quello aureo, ma è bene precisare che sarà sempre una approssimazione che non diventerà mai esatta poiché il rapporto aureo è un numero irrazionale, il che fa dei lati del rettangolo in esame due grandezze incommensurabili per le quali, cioè, non esiste un sottomultiplo comune; come si vede dall'immagine, il procedimento dei quadrati di Fibonacci crea invece lati sempre esprimibili tramite numeri interi, il che significa che il loro rapporto sarà sempre un numero razionale.
Particolarità geometriche[modifica | modifica wikitesto]

Dalla proprietà del rettangolo aureo di potersi "rigenerare" infinite volte, deriva la possibilità di creare al suo interno una successione infinita di quadrati e quindi una spirale, detta spirale di Fibonacci, in grado di approssimare la spirale aurea.

Spesso, per imprecisione, si è portati a scambiare detta spirale con l'autentica spirale aurea, ma si tratta di un errore: la spirale di Fibonacci, infatti, è data dall'unione di un'infinità di quarti di circonferenza, mentre la vera spirale aurea è un particolare tipo di spirale logaritmica, che si sovrappone soltanto parzialmente a quella di Fibonacci. Il grado di approssimazione, però, è talmente buono da notarsi difficilmente a occhio la differenza tra le due.
Ciò che, comunque, hanno in comune entrambe le spirali è il fatto di avvitarsi asintoticamente verso l'incrocio tra le diagonali che possono essere ricavate all'interno dei rettangoli aurei; punto di incontro che è stato chiamato da Clifford A. Pickover l'occhio di Dio.[2], proprio per il fatto che tutto sembra vertere attorno a questo punto, dalle spirali alle diagonali e alla sequenza di quadrati. Interessante notare, poi, come non soltanto le diagonali vere e proprie si intreccino in questo particolare punto del rettangolo aureo, ma anche altre rette colleganti ulteriori punti notevoli di questo vorticoso accentramento.
In geometria solida, il rettangolo aureo è presente in due solidi platonici, anch'essi legati alla sezione aurea:
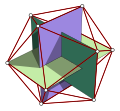
- nell'icosaedro, formato da 20 triangoli equilateri, i cui 12 vertici sono a gruppi di 4 disposti su 3 piani intersecantesi ortogonalmente; su questi è possibile, unendo i diversi punti, disegnare 3 rettangoli aurei disposti allo stesso modo.
- nel dodecaedro, formato invece da 12 pentagoni, gli stessi rettangoli aurei possono essere costruiti usando non i vertici, ma i centri delle facce; si tratta in realtà di una riproposizione della proprietà precedente, poiché tali centri sono i vertici di un icosaedro regolare.
Relazioni interne[modifica | modifica wikitesto]
All'interno di un rettangolo aureo possono ricavarsi una infinità di figure identiche legate tra loro in maniera sorprendente da relazioni strettissime con il numero aureo e le sue particolarità algebriche.[3]
Se consideriamo 1 la misura del lato minore del rettangolo aureo, quella del lato maggiore sarà φ; l'area complessiva del rettangolo risulterà quindi:
ovvero il numero aureo, mentre l'area del quadrato costruito al suo interno, sul lato minore, sarà 1, e il loro rapporto è quindi sempre pari a φ; il rapporto fra l'area del suddetto quadrato e quella del rettangolo aureo di completamento contestualmente creato, il cui lato minore misura φ - 1, sarà quindi:
- .[3]
Da ciò si ottiene che il rapporto fra due rettangoli aurei consecutivi nella successione è φ2, cosa che vale peraltro anche per i rispettivi quadrati. Iterando il procedimento si ottiene che:
- φ2n è il rapporto tra le aree del rettangolo (o quadrato) maggiore e l'n-esimo dei rettangoli (o quadrati) più piccoli.
- φ2n - 1 è il rapporto fra le aree del rettangolo (o quadrato) maggiore e l'n-esimo dei quadrati (o rettangoli) più piccoli. Si ha quindi una successione geometrica, a base aurea, i cui termini pari e dispari rappresentano rispettivamente rapporti fra figure simili e diverse.

Osservando le precedenti figure si capisce facilmente che la somma infinita di tutti i quadrati ricavabili, pari al rettangolo aureo stesso, è data dalla serie geometrica:
- 1 + φ-2 + φ-4 + φ-6 + ...
la cui somma è:
Questo risultato va interpretato come rapporto tra l'area totale e quella, considerata unitaria, del quadrato costruito sul lato minore del rettangolo aureo. Tale area è quella del quadrato costruibile sul lato maggiore; difatti disponendo adeguatamente tutti i rettangoli aurei si può ottenere un quadrato, come si vede nella figura a lato.
Dalla figura si evince anche che considerando solo la somma di tutti i rettangoli aurei interni, l'area totale è pari invece al quadrato costruibile sul lato lato minore del rettangolo aureo preso in considerazione; infine è possibile dire che dato un rettangolo aureo, sommando a questo tutti i suoi rettangoli interni (con cui costituisce un'area pari al già citato quadrato) e tutti i quadrati, sempre interni, l'area complessiva che si ottiene è quello del rettangolo aureo ad esso maggiore, procedendo ora non verso l'interno ma verso l'esterno della successione di figure.
Venendo ora ai perimetri, il perimetro di un rettangolo aureo vale 2φ2
mentre rispetto a questo il perimetro del rettangolo appena più interno vale:
Il rapporto fra due perimetri consecutivi è quindi esattamente φ (identica relazione vi è tra i perimetri dei rispettivi quadrati); siamo così di fronte questa volta a una successione del tipo:
- 1, φ-1, φ-2, φ-3, φ-4, φ-5 ...
la cui somma applicando il procedimento già visto è
La somma di tutti i suddetti perimetri è quindi pari al perimetro del rettangolo aureo ottenuto spostandosi due volte verso l'esterno nella solita successione.
Il rettangolo più bello[modifica | modifica wikitesto]
La sezione aurea è da sempre stata ritenuta un rapporto dotato di grande armonia, capace di conferire intrinsecamente bellezza alle figure, e fra tutte le sue applicazioni geometriche il rettangolo aureo è senz'altro il poligono che ha ereditato maggiormente tale fama. A torto o a ragione, si è ritenuto che fin dall'antichità sia stato usato nella costruzione di importanti edifici per conferire loro una particolare armonia; tali convinzioni non hanno però mancato di suscitare tra gli studiosi perplessità e a volte anche lunghe polemiche.
Forse, la diatriba più avvincente in merito, è quella che vede al centro il Partenone di Atene: molti studiosi[4] sostengono, per esempio, che la facciata possa essere interamente inquadrata in un ideale rettangolo aureo e a conferma di ciò vi sarebbero anche buona parte dei fregi, a loro volta basati su proporzioni interne e distanze che spesso sarebbero tra loro nello stesso particolare rapporto.
Vi è però anche una nutrita schiera di critici, che ritengono tale convinzione frutto di arbìtri, imprecisioni e autoconvincimento. Viene ad esempio contestato il modo in cui cambiano le misure da fonte a fonte, in relazione ai punti presi in considerazione, per farli quadrare con la suesposta tesi, a volte omettendo o includendo il basamento, altre ritagliando gli elementi "marginali" dell'architettura[5]; oppure si sottolinea come spesso le considerazioni vengano fatte non su dati reali, ma ricavando i disegni direttamente da foto o immagini prese in diverse angolature.
Si può anche rilevare che le prime testimonianze scritte sulla sezione aurea e sulla costruzione del rettangolo aureo sono contenute negli Elementi di Euclide (circa 300 a.C.), mentre la costruzione del Partenone risale al V secolo (terminò intorno al 438 a.C.), quindi più di cento anni prima, anche se ciò non toglie che ben prima di Euclide altri matematici e artisti ne fossero comunque a conoscenza; in ogni caso la tesi secondo la quale l'architettura del celebre monumento sarebbe basata sulla sezione aurea appare indimostrabile.[senza fonte]

Quanto alla facciata del Palazzo di Vetro, ovvero la sede centrale delle Nazioni Unite, che diverse fonti portano come ulteriore esempio, questa volta moderno, di applicazione della sezione aurea in architettura, è facile arrivare ad una conclusione negativa. Il palazzo è infatti alto 154 m e largo 87,5 m[6], quindi il rapporto fra le due dimensioni della facciata è 1,76: un rapporto che solo molto grossolanamente può essere considerato vicino a phi e certo non permettere di annoverare tale edificio fra quelli basati sul rettangolo aureo.

Nell'arte pittorica addirittura i riscontri sarebbero ancora più numerosi, specie nell'arte rinascimentale e soprattutto nei dipinti leonardeschi fra cui celeberrimo sarebbe il caso del San Gerolamo (la cui figura, omettendo il braccio, sarebbe compresa in un rettangolo aureo), nonché suoi diversi studi; non mancano anche esempi più recenti specie nelle correnti più astratte. In quest'ultimo caso vi è da dire che alcuni artisti hanno espressamente ammesso di aver fatto un uso volontario, seppur sporadico, del rettangolo aureo nelle loro opere, per altri si tratta invece di pure congetture derivanti da misurazioni e talvolta considerando valide pure grossolane approssimazioni. Non si può escludere un uso consapevole della sezione aurea da parte di Leonardo da Vinci: ricordiamo infatti che egli aveva disegnato alcune illustrazioni per l'opera di Luca Pacioli dedicata alla divina proporzione. Altri studiosi hanno invece ipotizzato che nel caso di Leonardo l'eventuale presenza del rettangolo aureo sia dovuta alla reale presenza del rapporto aureo in alcune proporzioni del corpo umano, che il pittore riproduceva fedelmente.
Per quanto riguarda alcune forme di uso corrente, le carte di pagamento (bancomat e carte di credito) e in generale i tesserini plastificati in formato "badge" (86x54mm) sono ottime approssimazioni di rettangoli aurei. L'arrotondamento per difetto al millimetro pari è stato fissato per facilitarne la produzione standardizzata, sebbene la misura più perfetta sarebbe stata 87,37x54 oppure 86x53,15.
Il comune foglio A4 invece non è in rapporto aureo, in quanto misura 210x297mm. Il rapporto tra i lati, con ottima approssimazione, vale . Si tratta di una scelta voluta: i rettangoli di questa forma hanno la proprietà di essere simili a quelli ottenuti dimezzando il lato maggiore.
Un'altra curiosità riguarda il calcio: nonostante le dimensioni regolamentari dei campi fissassero limiti minimi e massimi che comprendono il caso dei rettangoli aurei (da 64x103 a 68x110) la FIFA ha emesso qualche anno fa una raccomandazione a favore della misura di 68x105, che non è in rapporto aureo.
Le indagini psicologiche[modifica | modifica wikitesto]

Le indagini psicologiche sull'argomento e i dibattiti in merito nascono nell'800, grazie agli esperimenti di Theodor Fechner, pioniere della psicologia sperimentale, che tentò di confermare sperimentalmente, come si credeva fermamente, la supposta superiorità estetica del rettangolo aureo attraverso una serie di indagini volte a dimostrarne la preferenza diffusa nell'uomo.
L'indagine si svolse secondo tre tipologie metodologiche complementari.
- Il metodo della scelta (Wahl): richiesta diretta ai soggetti di scegliere quale fra i rettangoli mostrato fosse per loro preferibile.
- Il metodo della produzione (Herstellung): si chiede ai soggetti di disegnare il rettangolo che ritengono più gradevole.
- Il metodo dell'uso (Verwendung): indagine oggettiva su campo misurando numerosi oggetti di uso quotidiano per verificarne la presenza del rapporto aureo.
Gli esiti furono pubblicati nel 1879 in un volume intitolato Vorschule der Aesthetik (Manuale di estetica); delle tre soltanto la prima indagine diede esito positivo, secondo le sue convinzioni, rilevando una preferenza del 35% per il rettangolo aureo. Subito, però, sorsero le prime contestazioni sia sulla correttezza del metodo seguito, sia, soprattutto, sull'oscurità procedurale del primo esperimento.
 |
Fechner aveva mostrato a 347 persone una disposizione di 10 rettangoli di uguale area con il rapporto tra i lati in ordine crescente (da 1:1 - quindi un quadrato - a 1:2,5), di cui il rettangolo aureo occupava la settima posizione, chiedendo poi quale giudicassero più gradevole, consentendo in caso di incertezza anche scelte multiple, che andavano a influire frazionalmente sul risultato[7].
Le prime critiche sorsero su tre ordini di osservazioni circa la metodologia con cui venne svolto l'esperimento:
- L'aver trascurato l'influsso dell'orientamento verticale o orizzontale[8] del rettangolo sulla scelta delle persone.[9];
- L'influenza della posizione mediana[10] sulla scelta dei soggetti. In pratica si ritiene che i soggetti potrebbero essere stati orientati a indicare il rettangolo aureo in quanto rappresentava la figura con le proporzioni medie tra quelle presentate; in questo caso il rettangolo occupava sempre la settima posizione per cui si trovava in posizione lievemente laterale.
- I soggetti non erano scelti a caso e soprattutto erano a conoscenze delle convinzioni dello scienziato, il che pone tutti i possibili problemi per i quali oggi si adotta il procedimento del doppio cieco.
Gli esperimenti di Fechner, sebbene soltanto uno avesse dato l'esito da lui sperato, aprirono in risposta un filone di indagini psicologiche perdurato tutto il '900, nelle quali la preferenza per la sezione aurea si dimostrò sempre più una chimera, fino a trovare definitiva conclusione negativa nell'ultimo decennio del secolo.
| T. H. Haines e A. E. Davies[11], per confutare i risultati di Fechner, presero due gruppi di persone (di 11 e 12 componenti) e un totale di circa 80 rettangoli di differenti proporzioni ma accomunati da almeno una delle grandezze in 4 classi; sottoposero al primo gruppo tutte e quattro le serie mischiate fra loro, mentre al secondo soltanto una, chiedendo sempre di indicare quale fosse la figura preferita. Considerando valide le scelte nel range tra 0,58 a 0,66, come rapporti vicini a Φ, la preferenza per il rettangolo aureo risultò in entrambi i gruppi di poco superiore al 12%, molto lontana dai valori di Fechner. | |
| Charles Lalo ripeté lo stesso esperimento di Fechner, presumibilmente con le stesse accortezze, chiedendo di indicare fra 10 rettangoli quale fosse il più gradevole e quale il meno, e ottenne similmente gli stessi risultati anche se con una sperequazione di scelta molto meno marcata fra i diversi rettangoli. | |
| Edward Lee Thorndike fece l'esperimento con 12 rettangoli e altre figure[12], chiedendo a oltre un centinaio di persone di indicare di volta in volta quale figura preferissero per prima, per seconda, per terza, e così via, fino ad ottenere per ciascuno un ordine di preferenza completo; i rettangoli erano disposti verticalmente e disposti in ordine crescente di larghezza. Nessun rettangolo risultò prevalente sugli altri, ma rilevò che il rettangolo aureo e i due immediatamente vicini venivano scelti tra i primi tre posti con una preferenze tra il 35% e il 45%.[13] | |
| C. O. Weber[14] utilizzò il metodo della paired comparisons, mostrando a 68 soggetti diverse coppie di rettangoli di uguale area, ottenute con un paniere di 9 rettangoli[15] utilizzabili, con l'accortezza che il rettangolo aureo e i due più simili comparissero complessivamente nel 44% delle comparazioni. L'esperimento venne replicato a distanza di due settimane con gli stessi soggetti; e emerse alcune preferenza significativa per una particolare proporzione.[13] | |
| Paul Farnsworth rese noti[16] gli esperimenti compiuti nel quinquennio precedente con la stessa metodologia di Weber a 22 soggetti, ma ponendo l'accento sull'orientamento; L'indagine evidenziò che in verticale risultava una preferenza per il rettangolo aureo, però quasi a pari merito con quello che invece venne preferito nel senso orizzontale[17]. In seguito, ripetendo l'esperimento con un campione 3 volte maggiore, la preferenza per il rettangolo aureo risultò invece nulla.[13] | |
| F. C. Davis[18] riprese il metodo della produzione facendo disegnare per due volte a 310 soggetti il rettangolo più gradito a 40 minuti di distanza. Nella produzione emerse una triplice preferenza per proporzioni simili ai rapporti √3, 2, √5[19], anche se lo stesso Davis ammise che era difficile notare differenza tra la radice di tre (1,732) e il numero aureo (1,618) | |
| G. G. Thompson[20] si concentrò sullo studio per età, selezionando 4 gruppi di 100 soggetti ciascuno dall'asilo, le scuole medie, le superiori, e università. I soggetti dovevano indicare in ordine di preferenza 12 rettangoli con proporzioni da 0.25 a 0.75; gli esiti furono che mentre i bambini non davano alcuna preferenza i ragazzi delle scuole intermedie preferivano invece i rettangoli più larghi, mentre solo gli studenti universitari concentrarono le loro preferenze sui rapporti da 0,55, 0,60 e 0,65 (le cui grado medio di preferenza[21] fu rispettivamente di 2,8 ; 3,5 ; e 3,6), quelli che si possono ritenere più simili al rettangolo aureo. Ipotizzò che la direzione mostrata dagli studenti universitari fosse a questo punto da imputare a una sorta di condizionamento culturale, che è assente nei bambini e si acquisisce col tempo.[13] | |
| B. Steele W. C. Shipley, P. E. Dattman[22] criticano il lavoro di Thompson per aver trascurato il fatto dell'area, replicano l'esperimento sempre sulle stesse fasce d'età ma presentando solo 6 rettangoli e badando a creare una serie, prima tenendo costante l'altezza e poi l'area; i risultati furono grossomodo simili, ma le preferenze degli adulti si erano focalizzate sul rapporto 0,65 anche se il grado medio di preferenza[21] peggiorò passando da 3,6 a 4,7.[13] | |
| S. Ross e C. W. Neinstedt[23] sempre interessati al filone dell'età, si focalizzarono alla comparazione tra le preferenze negli anziani e nei giovani sempre con lo stesso metodi di Thompson. Anche questa volta la preferenza dei giovani si concentrò lievemente attorno al rettangolo con rapporto pari a 0,65 mentre gli anziani presentarono preferenze decisamente disomogenee.[13] | |
| Michael Godkewitsch volle provare che la preferenza riscontrata da Fechner dipendeva dalla coincidenza con la posizione media che occupava il rettangolo aureo rispetto agli altri: presentò tre distinte serie di 9 rettangoli ciascuna, dove il rettangolo si trovava prima vicino al rettangolo dal rapporto più allungato, poi come mediano e infine vicino ai rapporti più corti; l'esito fu che la preferenza per il rapporto aureo di riscontrava solo laddove coincideva con l'essere il rettangolo dalle proporzioni mediane, cioè dove rappresentava quello più equilibrato. | |
| John Benjafield ripropone l'esperimento di Godkewitsch in due varianti per tenere conto di due aspetti secondo lui sottovalutati: l'area dei rettangoli e il meccanismo di scelta. Benjafield usò le stesse tre tipologie di serie, ma proponendole sia con rettangoli di diverse aree e proporzioni, che con rettangoli equiestesi, cioè di diverse proporzioni ma uguale estensione; per quanto riguarda il processo di scelta, esso si svolgeva a fasi, prima dividendo le figure piacevoli da quelle non, e successivamente ripetendo la scelta sulle prime, per tre volte, prima di identificare il rettangolo preferito. Gli esiti furono che: per le serie non equiestese la preferenza cadeva, in tutti e tre i casi, sulle figure "larghe", per quelli con area costante invece si mostrava una preferenza per il rettangolo aureo; quest'ultimo risultato è di fatto in linea con gli esperimenti di Fechner e Lalo che usarono anch'essi rettangoli di uguale area. |
Note[modifica | modifica wikitesto]
- ^ a b Corrado Falcolini, Numeri in un foglio di carta, in Archimede, 2 (2006). Il procedimento è illustrato anche, ma senza dimostrazione, in Piega e spiega la matematica dalla Germania all'Italia[collegamento interrotto], intervista a Corrado Falcolini dal portale online dell'Enciclopedia Italiana Treccani
- ^ probabilmente per la costante presenza della sezione aurea altresì detta "divina proporzione", da cui il richiamo al divino di Clifford surrogato da quello di Pacioli ideatore della formula.
- ^ a b c d Le proprietà algebriche del numero aureo sono tutte deducibili dalle relazioni (tra loro equivalenti): 1) φ2 = φ + 1; 2) 1/φ = φ - 1
- ^ ad esempio David Bergamini in Mathematics dice «The Parthenon ad Athens fits into a golden rectangle almost precisely once its ruined triangular pediment in drawn in. Though it incorporates many geometric balances, its builders in the fifth century B.C. probably had no conscious knowledge of the golden ratio». 1987 ISBN 0-8094-4083-0
- ^ George Markowsky, Misconceptions: The Greek Used Φ in Pathenon, in Misconceptions about the Golden; sulla rivista The College Mathematicals Journal (1992, 23-1 pp. 8-9)
- ^ Valori tratti da , Misconceptions: The UN Building Embodies the Ratio Φ, in Misconceptions about the Golden, George Markowsky pp. 12; i valori sono espressi in piedi
- ^ Ogni rettangolo scelto contava 1/2 se ne venivano scelti due, 1/3 se ne venivano scelti 3, ... (Bastioni, p. 20)
- ^ Non si hanno certezze sul reale orientamento con cui vennero presentati: Lalo (1908) e Zusne (1970) sostengono che venne usato un orientamento orizzontale; Farnsworth (1932), Eysenck eTunstall (1968), Berlyne (1971), invece, un orientamento verticale, ritenendo che fosse uno standard assodato di presentazione. (Green)
- ^ Nel 1966 H.R. Schiffman condusse un esperimento dove dopo aver fatto disegnare il rettangolo più gradevole chiedeva di orientarlo secondo nel senso preferito e vi fu una netta preferenza per la disposizione orizzontale (Zocchi); il risultato sarebbe supportato a livello teorico per la maggiore ampiezza del campo visivo in senso orizzontale piuttosto che verticale.
- ^ Fra l'altro Fechner fu uno dei primi studiosi ad introdurre l'uso della mediana quale indicatore di posizione preferibile alla media in certi casi
- ^ The psychology of aesthetic reaction to rectangular in Psychological Review, 11:248–281, 1904
- ^ Triangoli, croci e linee sempre in dozzina(Psychological Review, 24, 147-153, 1917.
- ^ a b c d e f Green.
- ^ (). The aesthetics of rectangles and theories of affection, in Journal of Applied Psychology, 15, 310-318, 1931
- ^ Le proporzioni erano secondo 5 rapporti "notevoli", √2, Φ, √3, 2, √5, e altri interpolati fra questi
- ^ Pubblicati in Preference for rectangles sul Journal of General Psychology, 7:479–481, 1932
- ^ Bastioni, p. 27.
- ^ Aesthetic proportion in American Journal of Psychology, 45, 298-302, 1933
- ^ per l'esattezza erano rispettivamente 1,72:1; 2,02:1; 2,22:1; inoltre è da ricordare che 2 è la radice di 4
- ^ The effect of chronological age on aesthetic preferences for rectangles of different proportions in Journal of Experimental Psychology, 36, 50-58. 1946
- ^ a b Il grado medio di preferenza indica la media delle posizioni di preferenza con cui i rettangoli furono scelti, cioè per primo, per secondo, per terzo, ecc.
- ^ The influence of size on preferences for rectangular proportion in children and adults in Journal of Experimental Psychology, 37:333–336, 1947.
- ^ Preferences for rectangular proportions in college students and the aged in Journal of Genetic Psychology, 78:153–158, 1951.
Bibliografia[modifica | modifica wikitesto]
- Manuel Bastioni, La favola della sezione aurea (PDF), in Indagini su Rennes-le-Château, n. 5, 2006, pp. 243-250.
- (EN) Christopher Green, All That Glitters: A Review of Psychological Research on the Aesthetics of the Golden Section, in Perception, vol. 24, n. 8, 2005, pp. 937-968, DOI:10.1068/p240937.
- Mario Livio, La sezione aurea, Milano, RCS, 2003, ISBN 88-17-87201-6.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su rettangolo aureo
Wikimedia Commons contiene immagini o altri file su rettangolo aureo
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) golden rectangle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Rettangolo aureo, su MathWorld, Wolfram Research.
- Alessandro Zocchi, La sezione aurea; Gli esperimenti psicologici per verificare la bellezza del rapporto aureo, su Cicap, 11 aprile 2005. URL consultato il 27 luglio 2022.









