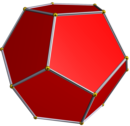
Icosaedro

Icosaedro
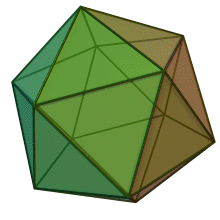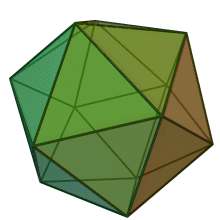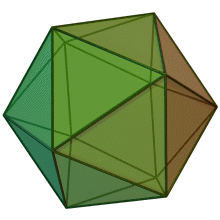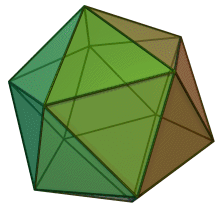Tipo	Solido platonico
Forma facce	Triangoli
Nº facce	20
Nº spigoli	30
Nº vertici	12
Valenze vertici	5
Notazione di Wythoff	5 | 2 3
Notazione di Schläfli	{3,5} s{3,4} sr{3,3} o $s{\begin{Bmatrix}3\\3\end{Bmatrix}}$
Diagramma di Coxeter-Dynkin
Duale	Dodecaedro
Proprietà	Non chirale
Politopi correlati
Figura al vertice Poliedro duale
Sviluppo piano

Modello 3D (in formato .stl) di un icosaedro

In geometria l'icosaèdro (dal latino icosahedrum, dal greco eikosi, che significa venti, e edra, che significa base) è un qualsiasi poliedro con venti facce. Con il termine icosaedro si intende però generalmente l'icosaedro regolare: nell'icosaedro regolare, le facce sono triangoli equilateri.

Solido platonico

L'icosaedro regolare è uno dei cinque solidi platonici (tetraedro, esaedro alias di cubo, ottaedro, dodecaedro, icosaedro). L'icosaedro ha 12 vertici e 30 spigoli. Il suo poliedro duale è il dodecaedro.

Area e volume

L'area della superficie A ed il volume V di un icosaedro regolare i cui spigoli hanno lunghezza a, sono dati dalle seguenti formule:

$A=5{\sqrt {3}}a^{2},$

$V={\begin{matrix}{5 \over 12}\end{matrix}}\left(3+{\sqrt {5}}\right)a^{3}.$

La costruzione di Euclide

Fig. 1: determinazione dello spigolo BM dell'icosaedro inscritto nella sfera di diametro AB

Fig. 2: costruzione dell'icosaedro

Fig. 3: icosaedro completo

Nel libro XIII dei suoi Elementi, Euclide descrive il metodo per inscrivere un icosaedro regolare in una sfera di diametro dato. La costruzione descritta da Euclide, lievemente semplificata, è la seguente:

Sia AB un diametro della sfera data; lo si divida nel punto C in modo che il segmento AC sia quattro volte il segmento CB (vedi Fig. 1). Si costruisca poi su AB un cerchio, si alzi la perpendicolare da C e si denoti con D uno dei due punti di intersezione tra tale perpendicolare e il cerchio. Infine, si congiungano i punti B e D: il segmento ottenuto è il raggio di quello che Euclide chiama "Cerchio su cui si descrive l'icosaedro".

Si tracci la perpendicolare al diametro AB passante per B (e giacente sul piano contenente il cerchio) e sia E uno dei due punti su tale perpendicolare tali che BD e BE abbiano uguale lunghezza. Si tracci quindi la retta passante per E e parallela ad AB e si denoti con M uno dei due punti di intersezione tra la retta e la circonferenza; infine si denoti con F l'intersezione tra AB e la parallela a BE passante per M e si traccino i segmenti FM e BM. Si ripeta quindi lo stesso procedimento partendo da A, trovando quindi il punto R antipodale ad M ed il punto G del diametro tale che AG=FB.

Le lunghezze di tutti questi segmenti si possono ricavare semplicemente applicando il secondo teorema di Euclide e il teorema di Pitagora; di seguito forniamo i valori delle loro lunghezze, una volta supposto che la sfera di partenza avesse diametro unitario.

Segmento	Lunghezza	Note
AB	$1$	Diametro della sfera in cui si vuole inscrivere l'icosaedro
AC, BC	${\frac {4}{5}},{\frac {1}{5}}$
CD	${\frac {2}{5}}$	Il triangolo ADB è rettangolo in D, CD è medio proporzionale fra AC e CB, ovvero fra 4/5 e 1/5
e BD, BE FM, RG	${\frac {\sqrt {5}}{5}}$	Ipotenusa del triangolo BCD che è rettangolo in C
d FB, AG	${\frac {1}{2}}-{\frac {\sqrt {5}}{10}}$	Il triangolo AMB è rettangolo in M: si calcola la proporzione FB: FM = FM: (1 - FB), FB coincide con il lato di un decagono regolare inscritto in un cerchio di raggio e
p AR, BM	${\sqrt {{\frac {1}{2}}-{\frac {\sqrt {5}}{10}}}}$	Ipotenusa del triangolo BFM che è rettangolo in F, BM coincide con il lato di un pentagono regolare inscritto in un cerchio di raggio e
GF	${\frac {\sqrt {5}}{5}}$	GF = AB - AG - FB. Coincide con e

Dalla tabella qui sopra si evince quanto segue:

• e è il lato dell'esagono, p del pentagono e d del decagono inscritti in un cerchio di raggio e,
• e, p e d sono lati di un triangolo rettangolo, come dimostrato da Euclide nel libro XIII dei suoi elementi,
• e coincide anche con il segmento GF.

Proseguendo con la costruzione, si replichi la costruzione delle linee BM MF, e AR RG, su quattro piani passanti per AB, con angolo diedro di 72° rispetto al piano iniziale (Fig. 2). Congiungendo in sequenza i punti M N O P Q, e R S T U V, si ottengono due pentagoni regolari inscritti nei cerchi di raggio e di centri F e G rispettivamente. Tutti i lati di questi pentagoni, come tutti i segmenti che partono dai punti A e B, hanno la stessa lunghezza, p, pari al lato del pentagono inscritto nel cerchio di raggio e (appunto il "Cerchio su cui si descrive l'icosaedro").

Rimane da verificare che la lunghezza delle congiungenti alternate fra i vertici dei due pentagoni sia pari a p. Sia Z il punto della circonferenza di centro G determinato prolungando il raggio RG. Chiaramente Z divide l'arco TU in due parti uguali e dunque le corde TZ e ZU sono uguali fra loro, e coincidono con il lato del decagono inscritto nel cerchio di raggio e. Ora gli angoli del poligono GZMF sono chiaramente tutti retti e, da quanto riportato nella tabella, si ha che i lati GF ed FM hanno la stessa lunghezza e quindi GZMF è un quadrato di lato e. Da ciò segue che il segmento TM è l'ipotenusa del triangolo rettangolo i cui cateti sono TZ (lato del decagono inscritto nel cerchio di raggio e) e ZM (lato dell'esagono inscritto nello stesso cerchio) e quindi la lunghezza di TM coincide anch'essa con il lato del pentagono inscritto nel cerchio di raggio e.

Ricapitolando (Fig. 3), si ha:

• i vertici M N O P Q, e R S T U V; si trovano tutti su archi di cerchio il cui diametro è AB (in figura è rappresentato solo il cerchio AMBR),
• i segmenti che partono dai vertici A e B (colorati in blu); i lati dei pentagoni M N O P Q e R S T U V (colorati in verde); e le diagonali alternate fra i vertici di questi due pentagoni (colorate in rosso) sono tutti spigoli dell'icosaedro, e hanno lunghezza pari al lato del pentagono inscritto nel cerchio di raggio e,
• il diametro AB della sfera in cui è inscritto l'icosaedro è quintuplo del quadrato del raggio e del "Cerchio su cui si descrive l'icosaedro",
• Per quanto riguarda la lunghezza dello spigolo, Euclide si limita a dimostrare che la sua lunghezza e il diametro della sfera sono incommensurabili. La lunghezza effettiva p è comunque calcolabile e, come riportato nella tabella, è

  $p={\sqrt {{\frac {1}{2}}-{\frac {\sqrt {5}}{10}}}}.$

Poliedro duale

Il poliedro duale dell'icosaedro è il dodecaedro.

Simmetrie

L'icosaedro possiede 120 simmetrie. Di queste, 60 sono rotazioni, mentre le altre invertono l'orientazione dello spazio.

Il gruppo di simmetria dell'icosaedro è quindi fatto di 120 elementi: è isomorfo al prodotto $A_{5}\times \mathbb {Z} /_{2\mathbb {Z} }$ fra il gruppo alternante $A_{5}$ di ordine $5!/2=60$ ed il gruppo ciclico di ordine 2. Le 60 rotazioni formano il sottogruppo $A_{5}\times \{0\}$, isomorfo ad $A_{5}$.

Il dodecaedro ha lo stesso gruppo di simmetrie. Altri solidi hanno questo gruppo di simmetria: tra questi, l'icosaedro troncato, che modellizza il pallone da calcio.

Voci correlate

• Solido platonico
• Dodecaedro

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «icosaedro»
• Wikimedia Commons contiene immagini o altri file sull'icosaedro

Collegamenti esterni

• Icosaedro, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Arturo Maroni, ICOSAEDRO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1933.
• Icoṡaèdro, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• icosaèdro, su sapere.it, De Agostini.
• Icosaedro, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) icosahedron, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Icosahedron, su MathWorld, Wolfram Research.
• (EN) Icosahedron, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.