Relazione d'ordine
In matematica, più precisamente in teoria degli ordini, una relazione d'ordine di un insieme è una relazione binaria tra elementi appartenenti all'insieme che gode delle seguenti proprietà:
Si definisce insieme parzialmente ordinato (oppure ordine) la coppia costituita da un insieme e da una relazione d'ordine su di esso. Le relazioni d'ordine si indicano spesso con i simboli , , e .
In lingua inglese un insieme parzialmente ordinato è anche detto concisamente poset (Partially Ordered Set), e questo termine è usato gergalmente anche nella lingua italiana.
Definizione
[modifica | modifica wikitesto]Dati due insiemi e , il loro prodotto cartesiano è l'insieme delle coppie ordinate definito nel modo seguente:[1]
Si definisce relazione binaria su un insieme un sottoinsieme del prodotto cartesiano .[2] Due elementi e sono messi in relazione da se:
e in tal caso si scrive .
Una relazione d'ordine è una relazione binaria tra elementi di un insieme riflessiva, antisimmetrica e transitiva.[3]
Esplicitamente, tale relazione soddisfa le seguenti proprietà:
Le relazioni d'ordine si indicano spesso con i simboli , , e .
La coppia costituita da un insieme e da una relazione d'ordine su di esso si dice insieme parzialmente ordinato o semplicemente ordine, da non confondere con il termine più specifico insieme totalmente ordinato.
Primi esempi
[modifica | modifica wikitesto]Esempi ben noti di insiemi parzialmente ordinati sono:
- gli insiemi numerici , , , muniti della relazione d'ordine totale standard ;
- l'insieme munito della relazione di divisibilità (cioè è un divisore di ).
Una qualunque famiglia di insiemi munita della relazione di inclusione (cioè è sottoinsieme di )
Ordine largo e ordine stretto
[modifica | modifica wikitesto]Alcuni autori[4] definiscono relazione d'ordine "stretto" una relazione che soddisfi le proprietà antiriflessiva, antisimmetrica e transitiva (o, equivalentemente e più concisamente, le proprietà asimmetrica e transitiva), e quindi chiamano relazione d'ordine "largo" la relazione d'ordine . L'ordine stretto mira a concentrarsi sulla asimmetria della relazione, non considerando la riflessività.
Benché le due definizioni siano distinte, il loro studio non presenta grosse differenze, in quanto tra le due classi di relazioni sussiste una corrispondenza biunivoca molto semplice.
Sia un insieme e denotiamo con la diagonale di , cioè , allora ad ogni relazione d'ordine largo è associata la relazione d'ordine stretto ; viceversa ad ogni relazione d'ordine stretto è associata la relazione d'ordine largo .
Digrafo di un ordine
[modifica | modifica wikitesto]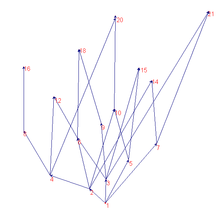
Se l'insieme è finito o numerabile la relazione d'ordine si può rappresentare visivamente mediante un digrafo (risp. finito o numerabile) i cui nodi sono gli elementi di e tale che due nodi e sono connessi da un arco se e solo se e non ci sono elementi intermedi tra di loro (cioè non esiste nessun tale che e ). Il grafo di una relazione d'ordine non può avere cicli, mentre può avere più componenti connesse e da ogni suo nodo può entrare ed uscire qualsiasi numero di archi. Se il grafo è numerabile, da un nodo possono entrare o uscire infiniti archi (questo è il caso della relazione di divisibilità).
Ordini semplici, lineari e totali
[modifica | modifica wikitesto]Due elementi e di un insieme parzialmente ordinato si dicono confrontabili se accade che oppure che .
In generale, due elementi di una relazione d'ordine parziale possono non essere confrontabili, cioè non sono necessariamente in relazione fra di loro. Ad esempio in munito della relazione di divisibilità, gli elementi 2 e 3 non sono in relazione perché nessuno dei due è divisore dell'altro.
Un insieme si dice un ordine semplice o lineare, oppure ordine totale se per ogni , e sono confrontabili (ossia vale oppure ).
Il digrafo di un insieme totalmente ordinato si può rappresentare come un segmento o una retta o una semiretta su cui giacciono tutti i nodi (corrispondenti a tutti gli elementi dell'insieme).
Catene e anticatene
[modifica | modifica wikitesto]Sia un ordine , si dice catena ogni sottoinsieme tale che la relazione d'ordine ridotta a costituisce un ordine semplice.
Si dice invece anticatena dell'insieme parzialmente ordinato un sottoinsieme i cui elementi sono mutuamente inconfrontabili. Una anticatena dell'insieme parzialmente ordinato delle divisibilità è fornita dall'insieme dei numeri primi.
Esempio
[modifica | modifica wikitesto]Per l'insieme parzialmente ordinato della divisibilità, sono catene gli insiemi delle potenze positive di un numero primo e più in generale i sottoinsiemi ottenuti con un processo che inizia considerando un intero positivo e prosegue aggiungendo ad ogni passo un multiplo dell'intero aggiunto in precedenza. Si possono considerare catene finite o infinite; il processo precedente può essere finito o illimitato.
Maggiorante e minorante
[modifica | modifica wikitesto]Sia un insieme parzialmente ordinato (poset) e . Allora si dice che un elemento è un maggiorante di se per ogni .
Analogamente, in modo duale, un elemento si definisce un minorante di un insieme se per ogni .
Se ammette almeno un maggiorante (minorante), allora si dice che è un sottoinsieme limitato superiormente (inferiormente).
Un sottoinsieme che possiede sia maggioranti che minoranti si dice limitato d'ordine.
Se l'insieme è un insieme numerico con cardinalità maggiore di uno (), allora scegliendo un suo sottoinsieme con cardinalità uguale a 2 (), si può definire il minimo tra i due soli elementi, e con la seguente relazione:
Il massimo tra i due elementi si trova invece con la seguente espressione:
dove con si è indicata la funzione indicatrice.
Elementi massimali e minimali
[modifica | modifica wikitesto]Sia un ordine. Si dice che è l'elemento minimo di se per ogni .
Si definisce elemento massimo di un tale che per ogni .
Vi sono ordinamenti per cui non esiste l'elemento minimo (rispettivamente, massimo); si mostra facilmente che se esiste un elemento minimo (rispettivamente, massimo) esso è unico. Quando esistono, l'elemento massimo e l'elemento minimo di si indicano rispettivamente come e .
Su ordini non semplici è utile definire altri due concetti: quello di elemento minimale e massimale.
- si dice elemento minimale di se .
- è invece un elemento massimale se .
In generale, massimo ed elemento massimale non corrispondono allo stesso elemento. Si consideri come esempio l'insieme fornito della relazione di divisibilità: esso non ammette né massimo né minimo, ma per esempio 3 è un elemento minimale, poiché è soddisfatto solo per . Si presti attenzione inoltre che l'elemento 3 non può essere massimale. Se così fosse, allora 3 non dividerebbe nessun altro elemento dell'insieme, ma che dimostra l'assurdità della asserzione dato che . Addirittura 5 è sia elemento massimale che minimale, poiché non è in relazione con nessun altro elemento dell'insieme diverso da se stesso. Dall'esempio è facile intuire che le due definizioni (massimo ed elemento massimale; minimo e elemento minimale) coincidono in presenza di un ordine semplice.
Estremo superiore ed inferiore
[modifica | modifica wikitesto]Sia un ordine e sia . Definiamo:
Allora si definiscono:
- estremo superiore di il ; quando esiste è indicato con ;
- estremo inferiore di il ; quando esiste è indicato con .
Osserviamo che, dato un sottoinsieme, non è detto che esso ammetta un minimo o un massimo, e dunque non è detto che esistano gli estremi superiori e inferiori.
Segmenti iniziali e finali
[modifica | modifica wikitesto]Sia un insieme ordinato e un sottoinsieme , allora è detto:
- segmento iniziale di , se dati due elementi e , si ha che ;
- segmento finale di , se analogamente .
In altre parole, gli elementi di non ammettono (rispettivamente) minimo o massimo al di fuori da .
Ordinamenti ben fondati
[modifica | modifica wikitesto]Una relazione d'ordine su un insieme si dice "ben fondata" o buon ordinamento se ogni sottoinsieme non vuoto è dotato di minimo.
Un tipico esempio di buon ordinamento è quello che stabilisce la relazione d'ordine standard sull'insieme dei numeri naturali. L'affermazione che i naturali sono un insieme ben ordinato, ossia che ogni sottoinsieme di ha un minimo viene talvolta chiamata principio del buon ordinamento e si può dimostrare essere equivalente al principio di induzione.
Il teorema del buon ordinamento
[modifica | modifica wikitesto]Il teorema del buon ordinamento (da non confondere con il principio del buon ordinamento) asserisce che su ogni insieme non vuoto può essere definita una relazione d'ordine ben fondata (o buon ordinamento). Tale enunciato è equivalente all'assioma della scelta (cioè assumendolo vero si può dimostrare l'assioma della scelta e viceversa).
Prodotto cartesiano di ordini
[modifica | modifica wikitesto]Il prodotto cartesiano di due insiemi parzialmente ordinati può essere munito anch'esso di un ordine in più modi:
- secondo il criterio dell'ordine lessicografico;
- secondo il confronto "termine a termine" se e (l'ordine così formato è detto il prodotto diretto dei due ordini);
- secondo la relazione se o .
Se i due ordini sono semplici, lo è anche l'ordine lessicografico, ma non necessariamente gli altri due.
Funzioni e relazioni d'ordine
[modifica | modifica wikitesto]Siano e due ordini e sia .
- si dice monotona se per ogni .
- si dice antitona se per ogni .
Note
[modifica | modifica wikitesto]- ^ Reed, Simon, Pag. 1.
- ^ Reed, Simon, Pag. 2.
- ^ Reed, Simon, Pag. 3.
- ^ Vincenzo Aversa, Metodi quantitativi delle decisioni. Algebra ed analisi elementare in una selezione di problemi di scelta, collana Manuali per l'università, Liguori Editore, 2000, pp. 12-15, ISBN 9788820731649.
Bibliografia
[modifica | modifica wikitesto]- Michael Reed, Barry Simon, Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis, 2ª ed., San Diego, California, Academic press inc., 1980, ISBN 0-12-585050-6.
Voci correlate
[modifica | modifica wikitesto]- Insieme totalmente ordinato
- Reticolo (matematica)
- Ordine denso
- Arborescenza, o albero con radice
- Teoria dei grafi
- Relazione di equivalenza
- Preordine
- Estremo superiore
- Condizione della catena ascendente
- Gruppo ordinato
- Campo ordinato
Collegamenti esterni
[modifica | modifica wikitesto]- relazione d'ordine, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Eric W. Weisstein, Partial Order, su MathWorld, Wolfram Research.
- (EN) Partial order, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
| Controllo di autorità | GND (DE) 4172733-2 |
|---|














![{\displaystyle [x\leq y\land y\leq x]\implies x=y,\qquad \forall x,y\in A;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1edfed8eace1d103ddce7ffaec6bc549db9a05bb)
![{\displaystyle [x\leq y\land y\leq z]\implies x\leq z,\qquad \forall x,y,z\in A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adcde71b4454c347af89c20150460f506be83d8c)







































































