Sistema di coordinate polari

In matematica, il sistema di coordinate polari è un sistema di coordinate bidimensionale nel quale ogni punto del piano è identificato da un angolo e da una distanza da un punto fisso detto polo.
Il sistema di coordinate polari è utile specialmente nei casi in cui le relazioni tra due punti possono essere espresse più facilmente in termini di angoli e di distanza; nel più familiare sistema di coordinate cartesiane, o sistema di coordinate rettangolari, tale relazione può essere espressa solamente tramite le funzioni trigonometriche.
Siccome il sistema di coordinate è bidimensionale, ogni punto è determinato da due coordinate polari: la coordinata radiale e quella angolare. La prima, di solito identificata con la lettera , denota la distanza del punto da un punto fisso detto polo (equivalente all'origine del sistema cartesiano). La coordinata angolare, solitamente denotata con la lettera greca θ, è anche detta angolo azimutale ed identifica l'angolo che la semiretta a 0° deve spazzare in senso antiorario per andare a sovrapporsi a quella che congiunge il punto al polo.
Storia[modifica | modifica wikitesto]
I concetti di angolo e raggio erano già utilizzati dai popoli antichi del I millennio a.C. L'astronomo greco Ipparco di Nicea (190-120 a.C.) costruì una tabella delle funzioni delle corde, che fornivano la lunghezza della corda sottesa da ogni angolo; esistono anche riferimenti all'utilizzo delle coordinate polari per stabilire le posizioni delle stelle.
Nel saggio Sulle Spirali, Archimede descrive la sua famosa spirale, una funzione il cui raggio dipende dall'angolo. L'opera dei greci, comunque, non si estese a un sistema di coordinate polari universalmente accettato.
Verso la metà del XVII secolo, Gregorio di San Vincenzo e Bonaventura Cavalieri introdussero, indipendentemente l'uno dall'altro, il concetto di coordinate polari. Il fiammingo Gregorio di San Vincenzo espose questo concetto nell'opera Opus geometricus del 1647, ma si ritiene che ne fosse a conoscenza dal 1625. Cavalieri pubblicò il suo lavoro nel 1635, ma nel 1653 fu stampata un'edizione più corretta. Cavalieri per primo utilizzò le coordinate polari per risolvere i problemi relativi al calcolo dell'area sottesa da una spirale di Archimede. Pascal, in seguito, utilizzò le coordinate polari per calcolare la lunghezza degli archi parabolici.
Nel Metodo per il calcolo differenziale (scritto nel 1671 e pubblicato nel 1736), Isaac Newton esaminò le trasformazioni che avvenivano tra le coordinate polari e quelle che sussistevano tra altri nove sistemi di coordinate.
Nel giornale Acta Eruditorum del 1691, Jacob Bernoulli utilizzò il sistema con un punto e una linea, che chiamò rispettivamente polo e asse polare. Le coordinate erano specificate dalla distanza dal polo e dall'angolo formato con l'asse polare; l'opera di Bernoulli si estese al calcolo del raggio di curvatura delle curve, espresse in queste coordinate.
Il termine coordinate polari è stato attribuito a Gregorio Fontana, e fu utilizzato dagli scrittori italiani del XVIII secolo. Alexis Clairaut fu il primo a pensare le coordinate polari in tre dimensioni, ed Eulero fu il primo a svilupparle effettivamente.
Individuazione dei punti in coordinate polari[modifica | modifica wikitesto]
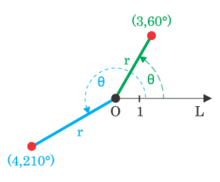
Ogni punto del sistema di coordinate polari può essere descritto con le due coordinate polari, di solito chiamate (coordinata radiale) e θ (coordinata angolare). La coordinata rappresenta la distanza radiale dal polo, mentre la θ è l'angolo in senso antiorario da percorrere partendo da 0° (asse di riferimento).
Ad esempio, le coordinate polari (3, 60°) devono essere disegnate con un punto posto a tre unità di distanza dal polo e in modo tale che la semiretta congiungente il punto al polo formi un angolo di 60° con l'asse di riferimento. È ovvio che il punto (3, -300°) coinciderà con il punto precedente, perché l'angolo -300° corrisponde esattamente all'angolo 60°; per la stessa proprietà degli angoli, anche tutti i punti (3, 60° + K×360°), con K numero intero, coincideranno con il primo punto, perché sommando o sottraendo angoli giri dallo stesso angolo, il risultato non cambia. In generale, tutti i punti identificati dalle coordinate (r, θ + K×360°) corrispondono allo stesso punto disegnato nel piano polare.
Ciò illustra un importante aspetto del sistema di coordinate polari, che non è presente in quello a coordinate cartesiane: ogni singolo punto può essere espresso con un numero infinito di coordinate differenti, ognuna delle quali è sfasata rispetto alle altre di un numero intero di angoli giri.
Le coordinate arbitrarie (0, θ) sono convenzionalmente utilizzate per rappresentare il polo, senza particolare interesse per il valore di θ, infatti ogni punto distante 0 dal polo coincide con il polo qualunque sia il suo angolo.
In notazione polare, gli angoli sono generalmente definiti in gradi o radianti, utilizzando la convenzione per cui 2π rad = 360°. Le applicazioni per la navigazione utilizzano maggiormente i gradi, mentre le applicazioni fisiche (specialmente in meccanica rotazionale) e quasi tutta la letteratura matematica sul calcolo utilizzano le misure in radianti.
Conversione da coordinate polari a cartesiane e viceversa[modifica | modifica wikitesto]
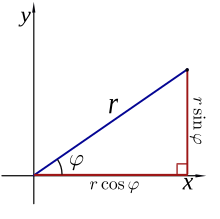
Le due coordinate polari e possono essere convertite nelle coordinate cartesiane e utilizzando le formule delle funzioni trigonometriche seno e coseno:
mentre le due coordinate cartesiane e possono essere convertite nella coordinata polare applicando il teorema di Pitagora:
- .
Per determinare invece la coordinata angolare , bisogna considerare i due seguenti casi.
- Se , allora può assumere qualunque valore reale.
- Se , allora per ottenere una rappresentazione univoca di , bisogna limitarsi a un intervallo di misura . Le scelte convenzionali in questo intervallo sono di solito o . Per ottenere il valore di nell'intervallo , possono essere utilizzate le seguenti formule (arctan è la funzione inversa della funzione trigonometrica tangente):
Per ottenere nell'intervallo , si usano invece le seguenti:
Un metodo alternativo di ricavare in termini di e è la seguente. Sfruttando un'identità trigonometrica
quindi
Il vantaggio di questo approccio è che vale questa unica formula per su tutto .
Moltissimi software (tra cui Microsoft Excel) e linguaggi di programmazione (tra cui Java) dispongono della funzione atan2 per passare dalle coordinate cartesiane a quelle polari.
Equazioni polari[modifica | modifica wikitesto]
L'equazione che definisce una curva algebrica espressa in coordinate polari è conosciuta come equazione polare. In molti casi, tale equazione può essere semplicemente espressa definendo come funzione di . La curva risultante consiste quindi dei punti della funzione e può essere considerata come il grafico della funzione polare di .
Dall'equazione della funzione polare di si possono dedurre diverse forme di simmetria. Se , la curva sarà simmetrica rispetto all'asse orizzontale, mentre se sarà simmetrica rispetto a quello verticale, e se , costituirà una simmetria rotazionale di in senso antiorario.
A causa della natura circolare del sistema di coordinate polari, molte curve possono essere descritte da una equazione polare piuttosto semplice, mentre la loro espressione cartesiana sarebbe più complicata. Tra le curve più conosciute di questa specie ci sono la rodonea, la spirale di Archimede, la lemniscata, il limaçon, e la cardioide.
Circonferenza[modifica | modifica wikitesto]

L'equazione generale della circonferenza con centro in (0, φ) e raggio è
Questa formula può essere semplificata in vari modi, per adattarla a casi più specifici, come l'equazione
per una circonferenza con centro nel polo e raggio .
Retta[modifica | modifica wikitesto]
Le rette radiali (che attraversano il polo) sono rappresentate dall'equazione
in cui φ è l'angolo formato dalla retta; cioè, φ = arctan dove è l'inclinazione della retta nel sistema di coordinate cartesiane. La linea non radiale che attraversa la retta radiale θ = φ perpendicolarmente nel punto (0, φ) ha equazione
Rodonea[modifica | modifica wikitesto]

Una rodonea è una celebre curva matematica che appare come un fiore con petali, e che si può esprimere semplicemente con un'equazione polare, data da
o
Posto come numero intero, l'equazione produrrà con dispari una rodonea di tipo , con pari di tipo . Se è invece un numero irrazionale, la curva formerà un disco. È da notare che queste equazioni non definiscono il numero dei petali della rosa; la variabile rappresenta solamente la lunghezza dei petali.
Spirale di Archimede[modifica | modifica wikitesto]

La spirale di Archimede è una famosa spirale che fu scoperta da Archimede, e che può essere espressa semplicemente con una equazione polare, della forma
Modificando il parametro , la spirale ruoterà, mentre controlla la distanza tra i bracci, che per una data spirale è sempre costante. La spirale di Archimede presenta due bracci, uno per θ > 0 e l'altro per θ < 0, ed entrambi si congiungono nel polo. Prendendo l'immagine speculare di un braccio lungo la retta 90°/270°, i due bracci si sovrappongono. Questa curva è notevole anche per essere stata una delle prime curve, dopo le sezioni coniche, ad essere descritta in un trattato matematico, e per essere stata il primo esempio di una curva che è rappresentata dalle coordinate polari meglio che dalle cartesiane.
Sezioni coniche[modifica | modifica wikitesto]

Una sezione conica con un fuoco sul polo e l'altro coincidente con un altro punto dell'asse a 0° (in modo che l'asse maggiore della conica possa giacere sull'asse polare) è data dall'equazione
in cui e è l'eccentricità della curva e è la perpendicolare al semiasse maggiore della curva. Se e > 1, questa equazione definisce un'iperbole, se e = 1, definisce una parabola e se e < 1, definisce un'ellisse. Il caso particolare in cui e = 0, riduce l'ellisse a una circonferenza di raggio .
Numeri complessi[modifica | modifica wikitesto]

Ogni numero complesso può essere rappresentato come un punto del piano complesso, e può quindi essere espresso sia in coordinate cartesiane (chiamata forma rettangolare) o nelle coordinate polari del punto (chiamata forma polare). Il numero complesso si rappresenta in forma rettangolare come
in cui è l'unità immaginaria, o può alternativamente essere scritto in forma polare come
e da qui come
in cui è il numero di Nepero. Le due formule sono equivalenti per quanto stabilito dalla formula di Eulero. Per convertire la forma rettangolare a polare e viceversa, si possono applicare le formule sopra citate.
Per le operazioni di moltiplicazione, divisione e esponenziale di numeri complessi, è in generale più semplice operare con i numeri complessi espressi in forma polare, piuttosto che in forma rettangolare. Infatti, per le regole degli esponenziali:
- Moltiplicazione:
- Divisione:
- Esponenziale (formula di De Moivre):
Traslazione in coordinate polari[modifica | modifica wikitesto]
Sfruttando la forma polare di un numero complesso si può arrivare alla formula della traslazione in coordinate polari. Presi due punti nelle coordinate polari e , espressi con la formula di Eulero sono
Se consideriamo il punto come punto traslato e come origine del nuovo asse, sia poi il punto non traslato, allora la traslazione è
Il modulo del numero complesso è un numero reale positivo definito come
Considerando ora un'equazione polare
Per applicare una traslazione alla funzione possiamo sostituire con la formula sopra, quindi
E l'equazione diventa
Se è una funzione costante allora la traslazione rappresenta una circonferenza in quanto l'equazione
rappresenta una circonferenza con centro l'origine è raggio il valore della costante. Nota che in termini geometrici la traslazione di un punto è la distanza tra il punto e l'origine del nuovo asse, come è ben visibile dalla formula stessa. Per convertire la curva traslata da coordinate polari a cartesiane dobbiamo prelevare il punto sulla curva in coordinate polari e trasformarlo in coordinate cartesiane, si ottiene semplicemente lo stesso sistema visto sopra, basta infatti prelevare il punto che è componente del punto .
Calcolo infinitesimale[modifica | modifica wikitesto]
Il calcolo infinitesimale può essere applicato alle equazioni espresse in coordinate polari. La coordinata angolare , in questa sezione, viene espressa in radianti, la scelta convenzionale nel calcolo infinitesimale.
Calcolo differenziale[modifica | modifica wikitesto]
Esistono le formule seguenti:
Oppure le inverse:
Per trovare la pendenza cartesiana della tangente alla curva polare in un dato punto, la curva viene per prima cosa espressa con un sistema di equazioni parametriche.
Derivando entrambe le equazioni rispetto a
Effettuando il rapporto tra la seconda e la prima equazione, si ottiene la pendenza della retta tangente alla curva nel punto (θ, r(θ)):
Calcolo integrale: area sottesa[modifica | modifica wikitesto]
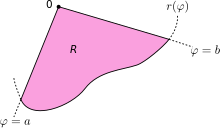
Se R indica la regione dello spazio racchiusa dalla curva r(θ) e dalle rette θ = a e θ = b, in cui 0 < b − a < 2π, allora l'area di R è espressa da
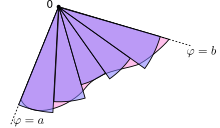
Si può giungere a questo risultato come segue: per prima cosa, l'intervallo [a, b] viene diviso in n sottointervalli, in cui n è un numero intero positivo arbitrario. Chiamata Δθ l'ampiezza di ogni sottointervallo, sussiste la relazione che Δθ è pari a b − a (l'ampiezza totale dell'intervallo), divisa per n, numero dei subintervalli. Per ogni sottointervallo, i = 1, 2, …, n, si chiama θi il suo punto medio, e si costruisce un settore circolare con centro nel polo, raggio r(θi), e angolo Δθ. L'area di ogni settore costruito è perciò pari a . L'area totale di tutti i settori sarà pertanto uguale a
Quando cresce il numero dei sottointervallo , l'approssimazione dell'area continua a migliorare. Al limite, per , la somma giunge ad essere la somma di Riemann per l'integrale precedente.
Calcolo integrale: lunghezza della linea[modifica | modifica wikitesto]
La lunghezza della linea espressa da una funzione polare, viene ottenuta per integrazione di segmenti infinitesimi lungo la curva r(θ) stessa. Usiamo L per denotare la lunghezza della linea a partire dal punto iniziale A fino al punto finale B, dove questi punti corrispondono a: = a , = b. La lunghezza L della linea è allora data dal seguente integrale:
- =
Generalizzazione[modifica | modifica wikitesto]
Utilizzando le coordinate cartesiane, un elemento infinitesimo di area può essere calcolato come . La regola della sostituzione per integrali multipli stabilisce che, passando ad altre coordinate, bisogna considerare il valore assoluto del determinante della matrice jacobiana:
Pertanto, un elemento di area in coordinate polari può essere scritto come
Ora, una funzione data in coordinate polari, può essere integrata come segue:
Qui è la stessa regione ricavata sopra, e corrisponde all'area racchiusa dalla curva e dalle rette e .
La formula per il calcolo di è stata ricavata assumendo identicamente uguale a . Un'applicazione sorprendente di questo risultato riguarda la possibilità di calcolare l'integrale di Gauss
Calcolo vettoriale[modifica | modifica wikitesto]
Le coordinate polari si possono applicare anche al calcolo vettoriale e, in particolare, allo studio della cinematica dei moti piani. Sia la posizione del vettore
espresso in un sistema di coordinate cartesiane di versori di base e , Il modulo e l'angolo polare dipendono dal tempo e descrivono il movimento di un corpo nel piano.
Siano il vettore unità (versore) nella direzione di e il versore dell'angolo di .
Le derivate prima e seconda del vettore posizione
sono, rispettivamente, il vettore velocità
ed il vettore accelerazione
del moto. Si ricorda che le derivate dei versori sono:
In tre dimensioni[modifica | modifica wikitesto]
Il sistema di coordinate polari si può estendere anche alle tre dimensioni, con due differenti sistemi di coordinate, quelle cilindriche e quelle sferiche, delle quali entrambe richiedono coordinate polari planari o bidimensionali come base. In sintesi, il sistema di coordinate cilindriche estende le coordinate polari aggiungendo un'altra coordinata della distanza, mentre le coordinate sferiche aggiungono un'altra coordinata angolare.
Coordinate cilindriche[modifica | modifica wikitesto]
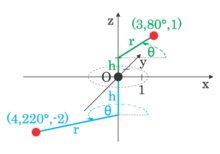
Il sistema di coordinate cilindriche è un sistema di coordinate che estende il sistema bidimensionale polare aggiungendo una terza coordinata, che misura l'altezza di un punto dal piano base, in modo simile a quello in cui si introduce la terza dimensione nel piano cartesiano. La terza coordinata è spesso chiamata , e l'intera terna è quindi .
Le tre coordinate cilindriche possono essere convertite in coordinate cartesiane con le formule
Coordinate sferiche[modifica | modifica wikitesto]

Le coordinate polari possono essere estese in tre dimensioni anche utilizzando le coordinate , in cui è la distanza dal polo, è l'angolo formato con l'asse e è l'angolo formato dalla proiezione sul piano , con l'asse . Questo sistema di coordinate, chiamato sistema di coordinate sferiche, è simile al sistema della latitudine e longitudine utilizzato per la Terra, con la latitudine che è il complementare di , se è l'asse di rotazione terrestre, determinato dalla relazione e la longitudine est (se compreso fra 0° e 180°) oppure la longitudine ovest (se è compreso fra -180° e 0°), se il semipiano con contiene il meridiano di Greenwich.

Le tre coordinate cartesiane di un punto si ottengono dalle tre coordinate sferiche di quel punto con le formule:
Applicazioni[modifica | modifica wikitesto]
Le coordinate polari sono bidimensionali, e pertanto possono essere utilizzate soltanto ove le posizioni dei punti giacciano su un singolo piano bidimensionale. Il loro utilizzo è appropriato in ogni contesto in cui il fenomeno considerato sia legato alla direzione e alla distanza da un certo punto; gli esempi sopra mostrati mostrano come elementari equazioni polari siano sufficienti a definire curve – come la spirale di Archimede – la cui equazione in coordinate cartesiane sarebbe molto più intricata. Inoltre, molti sistemi fisici – come quelli riguardanti i corpi che si muovono intorno a un punto centrale e con fenomeni originanti da un punto centrale – possono essere trattati in modo più semplice e più intuitivo utilizzando le coordinate polari. La motivazione iniziale per l'introduzione del sistema polare fu lo studio del moto circolare e del moto orbitale.
[modifica | modifica wikitesto]
Le coordinate polari sono spesso utilizzate nella navigazione, quando la destinazione o la direzione del viaggio possono essere forniti attraverso un angolo e una distanza dal luogo di arrivo. Ad esempio, gli aeroplani utilizzano una versione leggermente modificata delle coordinate polari per la navigazione. In questo sistema, gli angoli sono considerati in senso orario. L'angolo a 360° (0°) corrisponde al nord magnetico, mentre gli angoli a 90°, 180° e 270° corrispondono all'est magnetico, sud magnetico e ovest magnetico rispettivamente. Pertanto, un aeroplano che viaggia a 5 miglia nautiche a est starà viaggiando a 5 unità verso l'angolo di 90°.
Modelli[modifica | modifica wikitesto]
I sistemi che mostrano una simmetria radiale sono l'ambiente ideale per l'applicazione delle coordinate polari, con il punto centrale che agisce da polo. Sistemi con una forza centrale sono anche potenziali candidati all'utilizzo delle coordinate polari: questi sistemi includono i campi gravitazionali, che obbediscono alla legge dell'inverso del quadrato, come anche i sistemi con una sorgente puntiforme, come le radio antenne.
Bibliografia[modifica | modifica wikitesto]
- (EN) Irl Bivens e Stephen Davis, Calculus., 7th ed., Wiley, 2002, ISBN 0-471-38157-8, OCLC 46240252.
- (EN) Ross L. Finney, Calculus : graphical, numerical, algebraic : single variable version, Addison-Wesley, 1995, ISBN 0-201-55478-X, OCLC 28844114.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sul sistema di coordinate polari
Wikimedia Commons contiene immagini o altri file sul sistema di coordinate polari
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) polar coordinates, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Sistema di coordinate polari, su MathWorld, Wolfram Research.
- Coordinate geografiche polari (PDF), su physics.oregonstate.edu.
- Applicazione per la conversione delle coordinate da cartesiane a polari [collegamento interrotto], su sourceforge.net.
| Controllo di autorità | GND (DE) 4323692-3 |
|---|










![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)

































































![{\displaystyle L=\int _{a}^{b}{\sqrt {\left[r(\theta )\right]^{2}+\left[{{dr(\theta )} \over {d\theta }}\right]^{2}}}d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4238d39d4941e495ae8f630d7f8eb575a6a600)
![{\displaystyle \int _{\theta _{A}}^{\theta _{B}}{\sqrt {\left[r(\theta )\right]^{2}+\left[{{dr(\theta )} \over {d\theta }}\right]^{2}}}d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5344a9f96ed25b4d1ab40549bb26bea09cecb5c6)


















![{\displaystyle \mathbf {a} (t)={\frac {d^{2}\mathbf {r} }{dt^{2}}}=\left[{\frac {d^{2}r}{dt^{2}}}-r(t)\left({\frac {d\theta }{dt}}\right)^{2}\right]\,{\hat {\mathbf {r} }}(t)+\left[r(t){\frac {d^{2}\theta }{dt^{2}}}+2{\frac {dr}{dt}}{\frac {d\theta }{dt}}\right]\,{\hat {\boldsymbol {\theta }}}(t).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c35a9740d75a5797a524388d485033f7f6aec3f2)















