Ottaedro

Ottaedro
Tipo	Solido platonico
Forma facce	Triangoli
Nº facce	8
Nº spigoli	12
Nº vertici	6
Valenze vertici	4
Notazione di Wythoff	4 | 2 3
Notazione di Schläfli	{3,4} r{3,3}
Diagramma di Coxeter-Dynkin
Gruppo di simmetria	$S_{4}\times \mathbb {Z} _{2}$
Duale	Cubo
Proprietà	non chirale
Politopi correlati
Figura al vertice Poliedro duale
Sviluppo piano

Modello 3D (in formato .stl) di un ottaedro

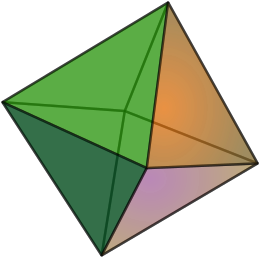
In geometria solida, l'ottaedro è un poliedro con otto facce triangolari. L'ottaedro regolare è uno dei cinque solidi platonici, le cui facce sono triangoli equilateri. Ha sei vertici e dodici spigoli.

Area e volume

L'area $A$ di superficie e il volume $V$ dell'ottaedro regolare il cui spigolo ha lunghezza $a$ e la diagonale ha lunghezza $d=a{\sqrt {2}}$ sono date da:

$A=2{\sqrt {3}}a^{2}\approx 3,46410162a^{2};$

$V={1 \over 6}d^{3}={\frac {1}{3}}{\sqrt {2}}a^{3}\approx 0,471404521a^{3}.$

Il volume è 4 volte quello di un tetraedro regolare con spigoli di lunghezza $a$, mentre l'area di superficie è il doppio (poiché è formata da 8 triangoli equilateri, contro i 4 del tetraedro)

L'angolo diedrale dell'otteadro regolare è

$\arccos \left(-{\frac {1}{3}}\right)\approx 109,47122^{\circ },$

dove $\arccos$ è la funzione arcocoseno.

Coordinate cartesiane

Un ottaedro regolare nello spazio euclideo $\mathbb {R} ^{3}$ può essere traslato in modo da avere il centro nell'origine, e dopo opportune rotazioni e similitudine ha i 6 vertici in

$(\pm 1,0,0),$

$(0,\pm 1,0),$

$(0,0,\pm 1).$

La costruzione di Euclide

Fig. 1: determinazione dello spigolo AC dell'ottaedro inscritto nella sfera di diametro AB

Fig. 2: costruzione dell'ottaedro

Nel libro XIII dei suoi Elementi, Euclide descrive il metodo per inscrivere un ottaedro regolare in una sfera di diametro dato. La costruzione descritta da Euclide è la seguente:

Sia $AB$ (vedi Fig. 1) il diametro della sfera data; si trovi il suo punto medio $D$ e si tracci un semicerchio di centro $D$ e raggio $DA$. Si alzi la perpendicolare da $D$, determinare il punto $C$ sulla circonferenza e infine si congiungano i punti $AC$ e $CB$.

Si replichi la stessa costruzione sui tre piani passanti per $AB$ con angolo diedro di 90°, 180° e 270° rispetto al piano iniziale (Fig. 2). Si traccino infine le congiungenti fra i punti $CE,EF,FG$ e $GC$.

È chiaro che i vertici $A,C,E,F$ e $G$ si trovano sulle semicirconferenze costruite sul diametro $AB$, quindi si trovano tutti sulla superficie della sfera di pari diametro. Per costruzione gli spigoli che partono dai vertici $A$ e $B$ sono uguali fra loro; ma anche gli spigoli $CE,EF,FG$ e $GC$ hanno la stessa lunghezza: infatti tutti gli spigoli dell'ottaedro risultano essere ipotenusa di un triangolo rettangolo i cui cateti sono raggi della sfera.

Per quanto riguarda il rapporto fra diametro della sfera spigolo dell'ottaedro inscritto, per il teorema di Pitagora il quadrato costruito sullo spigolo è doppio del quadrato costruito sul raggio della sfera; di conseguenza il quadrato costruito sul diametro è doppio del quadrato costruito sullo spigolo.

Poliedro duale

Il poliedro duale dell'ottaedro regolare è il cubo.

Simmetrie

L'ottaedro ha 24 simmetrie rotazionali, cioè che preservano l'orientazione dello spazio, più altre 24 simmetrie che non la preservano. Il gruppo di simmetria dell'ottaedro consta quindi di un totale di 48 elementi.

Il sottogruppo dato dalle 24 rotazioni è isomorfo al gruppo $S_{4}$ delle permutazioni di 4 elementi. Vi è infatti esattamente una rotazione che realizza ogni possibile permutazione delle 4 coppie di facce opposte.

Il gruppo totale di simmetria è isomorfo al prodotto $S_{4}\times \mathbb {Z} /2\mathbb {Z}$ di $S_{4}$ con un gruppo ciclico con 2 elementi.

Tassellazioni

Una tassellazione dello spazio con ottaedri e tetraedri.

Dettaglio della tassellazione.

L'ottaedro regolare non genera da solo una tassellazione dello spazio, perché i suoi angoli diedrali non sono divisori di 360°. Ne genera una però in combinazione con il tetraedro, come mostrato in figura.

Voci correlate

• Solido platonico
• Ottaedro troncato
• Ottaedro iperbolico

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «ottaedro»
• Wikimedia Commons contiene immagini o altri file sull'ottaedro regolare

Collegamenti esterni

• Ottaedro, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Arturo MARONI e Ugo PANICHI, OTTAEDRO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1935.
• Ottaedro, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
• Ottaèdro, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• ottaèdro, su sapere.it, De Agostini.
• Ottaedro, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Regular Octahedron, su MathWorld, Wolfram Research.
• (EN) Octahedron, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Bipiramidi regolari n-gonali:

Bipiramide	Bipiramide digonale	Bipiramide triangolare (Vedi: J12)	Bipiramide quadrata (Vedi: O)	Bipiramide pentagonale (Vedi: J13)	Bipiramide esagonale	Bipiramide ettagonale	Bipiramide ottagonale	Bipiramide ennagonale	Bipiramide decagonale	...	Bipiramide apeirogonale
Immagine del poliedro										...
Immagine della tassellatura sferica										Immagine della tassellatura del piano
Incidenza	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagramma di Coxeter-Dynkin										...

Controllo di autorità	GND (DE) 4338158-3