Ingranaggio

Un ingranaggio è un meccanismo utilizzato per trasmettere un momento meccanico da un oggetto a un altro.Generalmente è costituito da due o più ruote dentate, che possono essere di uguale o diversa dimensione. La ruota più piccola è comunemente chiamata pignone, mentre la grande è chiamata corona.
Sebbene le ruote dentate siano state considerate per lungo tempo un'invenzione umana, nel 2013 si è scoperto che strutture assimilabili a ruote dentate sono presenti anche in natura, in particolare sono state osservate nelle articolazioni delle zampe della ninfa di Issus appartenente alla superfamiglia Fulgoroidea.[1]
Una ruota settoriale è un settore circolare di una ruota completa: lavora solamente sulla parte dentata ed è impiegata dove non è necessaria la rotazione continua, col vantaggio di risparmiare peso e ingombro.
Storia[modifica | modifica wikitesto]

I primi esempi di ingranaggi risalgono al IV secolo a.C. in Cina[2] (periodo delle Zhan Guo - fine della dinastia Zhou orientale), che sono stati conservati presso il Museo di Luoyang nella Provincia di Henan, Cina. Gli ingranaggi più antichi conservati in Europa sono stati trovati nel meccanismo di Anticitera, un esempio di dispositivo a ingranaggi molto antico e complesso, progettato per calcolare le posizioni astronomiche. La sua data di costruzione è ora stimata tra il 150 e il 100 a.C.[3] Gli ingranaggi appaiono in opere legate a Ero di Alessandria, nell'Egitto romano circa nel 50 d.C.,[4] ma possono essere fatti risalire alla meccanica della Biblioteca di Alessandria nell'Egitto tolemaico del III secolo a.C., e furono ampiamente sviluppati dal polimata greco Archimede (287-212 a.C.).[5]

Un complesso dispositivo calendario a ingranaggi che mostra la fase della Luna, il giorno del mese e le posizioni del Sole e della Luna nello Zodiaco è stato inventato nell'Impero bizantino all'inizio del VI secolo d.C.[6] L'ingranaggio a vite senza fine è stato inventato nel subcontinente indiano, per l'uso in gualcitori di cotone, in qualche momento tra il XIII e il XIV secolo.[7] Gli ingranaggi differenziali possono essere stati usati in alcuni dei carri che indicano il sud cinesi,[8] ma il primo uso verificabile di ingranaggi differenziali è stato da parte dell'orologiaio britannico Joseph Williamson nel 1720.
Esempi delle prime applicazioni di ingranaggi includono:
- 1386 d.C.: L'Orologio della Cattedrale di Salisbury: è l'orologio meccanico a ingranaggi ancora funzionante più antico al mondo.
- L'Astrolabio di Giovanni Dondi dell'Orologio era un complesso orologio astronomico costruito tra il 1348 e il 1364 da Giovanni Dondi dell'Orologio. L'Astrolabio aveva sette facce e 107 parti mobili; mostrava le posizioni del sole, della luna e dei cinque pianeti allora conosciuti, così come le festività religiose.[9]
- circa XIII-XIV secolo: L'ingranaggio a vite senza fine è stato inventato come parte di un gualcitore di cotone nel subcontinente indiano.[7]
- circa 1221 d.C.: L'astrolabio a ingranaggi è stato costruito a Isfahan, mostrando la posizione della luna nello zodiaco e la sua fase lunare, e il numero di giorni dalla nuova luna.[10]
- circa VI secolo d.C.: Un dispositivo calendario a ingranaggi che mostra la fase della Luna, il giorno del mese e lo Zodiaco è stato inventato nell'Impero bizantino.[6][11][12]
- 725 d.C.: I primi orologi meccanici a ingranaggi furono costruiti in Cina.
- II secolo a.C.: Il meccanismo di Anticitera, il più antico computer analogico del mondo, è stato costruito. Poteva prevedere il movimento e la posizione del sole, della luna e dei pianeti decenni in anticipo e risolvere diversi problemi astronomici.[13][14]
- circa 200-265 d.C.: Ma Jun ha utilizzato ingranaggi come parte di un cavallo che indica il sud.
- In natura: nelle zampe posteriori delle ninfe dell'insetto Issus coleoptratus.
Descrizione[modifica | modifica wikitesto]

Ruote di diversa dimensione sono spesso usate in coppia per aumentare il momento meccanico riducendo nel contempo la velocità angolare, o viceversa aumentare la velocità diminuendo il momento. È il principio alla base del cambio automobilistico.
La trasmissione tra ruote non dentate avviene grazie all'attrito che si sviluppa nell'accoppiamento: si parla quindi di ruote di frizione. Perché essa avvenga è perciò necessario che la forza periferica imposta dal momento meccanico che si vuole trasmettere non superi l'attrito dell'accoppiamento. Per la trasmissione di potenze più elevate si ricorre allora a ruote dentate, cui d'ora in avanti ci si riferirà esclusivamente come ruote, che si suddividono in più famiglie a seconda della base della sezione (circolari e no), dell'andamento di tale sezione con la dimensione perpendicolare al piano di sezione (cilindriche, coniche, toroidali), del profilo dei denti (evolvente, spirale, profili corretti).
Le ruote dentate sono fabbricate per impronta con un'opportuna dentiera (cilindriche), o corona (coniche), oppure per intaglio da speciali macchine fresatrici, dette dentatrici. Per il montaggio sull'albero motore hanno solitamente una guida nel foro interno per la chiavetta di Woodruff, altrimenti, come negli ingranaggi del cambio, hanno delle scanalature per alberi a millerighe.
Disposizione della dentatura[modifica | modifica wikitesto]

La dentatura di un ingranaggio può essere posta in vari modi:
- esterna: questa è la disposizione classica di un ingranaggio; dà all'elemento una forma raggiata, con i denti rivolti verso l'esterno.
- interna: questa disposizione lascia il bordo esterno liscio, mentre nella parte interna sono presenti i denti, col vantaggio di avvicinare gli assi paralleli di corona e pignone. Per queste ruote si considera convenzionalmente negativo il diametro della corona, poiché in questo caso la velocità trasmessa è equiversa a quella conducente.
- laterale: questa disposizione fa assumere all'ingranaggio una forma simile a una corona di un re.
Ruote circolari[modifica | modifica wikitesto]
La trattazione seguente è tra le più semplici, e permette di confrontare direttamente una trasmissione a ingranaggio con la trasmissione di una puleggia. In effetti, si può pensare di partire da due semplici pulegge circolari che si trasmettono il moto per attrito: se l'attrito non è sufficiente a trasmettere la coppia, si può aumentare la coppia trasmissibile indentando le due ruote. A questo punto la coppia massima teoricamente diventa quella a cui si rompe una delle due ruote. Le pulegge originarie rimane la rulletta del moto. La circonferenza ideale di una ruota dentata equivalente a quella della puleggia originaria si chiama circonferenza primitiva, ed è il punto di partenza del progetto di una ruota dentata. Il diametro della circonferenza primitiva è detto semplicemente diametro primitivo. La primitiva può anche non essere circolare: per esempio, nel caso di ruote ellittiche, la primitiva è una ellisse (camma ellittica). Più in generale, si può pensare di indentare una camma, nel caso l'attrito volvente in alcuni istanti di moto non sia sufficiente a garantire la trasmissione. Per prima cosa quindi un progettista verificherà se l'attrito volvente non basta già a garantire la trasmissione: la dentatura aumenta sempre il costo della ruota (o camma). Una volta definite le primitive, si passa a progettare la dentatura.
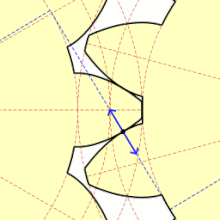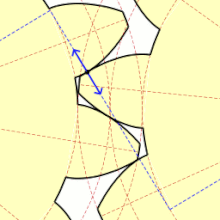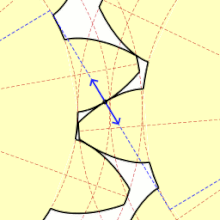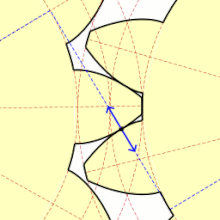
Come secondo parametro nella sequenza logica, solitamente si definisce il numero dei denti, o meglio il modulo. In seguito si passa a definire le circonferenze di base e di testa: il punto di contatto tra i denti delle due ruote giacerà sempre vicino alla primitiva. I denti quindi devono partire sotto la primitiva e finire sopra la primitiva: è intuitivo che la distanza della base e della testa (sono entrambe circonferenze, nel caso di ruote circolari) dalla primitiva dipenda in primo luogo dal numero dei denti, ovvero dal modulo. Esistono diversi standard di ruote dentate: queste due distanze di progetto variano leggermente da uno standard all'altro.
Infine, si individua il profilo dei denti. Inizialmente il profilo dei denti utilizzato fu a cicloide; da decenni si è passati invece al profilo a evolvente di cerchio. Il profilo a evolvente minimizza usura, vibrazioni e rumore, e massimizza il rendimento.
Vi sono due tangenti alle due basi passanti per C: a seconda della direzione del moto di rotazione relativa fra le due ruote, si individua quale delle due è la retta di contatto. In assenza di attrito la direzione lungo la quale i profili dei denti si toccano durante l'ingranamento, scambiandosi la mutua sollecitazione, coincide con essa. L'arco di primitiva e il segmento di retta d'azione corrispondenti alla rotazione delle due primitive, durante la quale si ha almeno una coppia di denti in presa, sono detti rispettivamente arco e segmento d'azione. Quest'ultimo è rappresentato in figura dalla porzione di segmento blu compresa tra la posizione occupata all'accesso e quella occupata al recesso del contatto tra due denti coniugati (rispettivamente dove il punto incomincia e dove finisce il suo moto periodico).
Rapporto di trasmissione[modifica | modifica wikitesto]
Detto angolo di pressione l'angolo (in C) fra la retta di contatto e la tangente alle due primitive, i raggi delle due circonferenze sono legati dalla relazione raggio circonferenza di base, con raggio della primitiva. Generalmente l'angolo di pressione varia da 15 a 20° e il suo valore modifica il profilo dei denti.[15]
Perciò il rapporto di trasmissione dipende unicamente dalle basi, ed è indipendente dall'interasse i:
La distanza fra due punti omologhi di due denti consecutivi, misurata lungo una circonferenza, è denominata passo della dentatura, suddivisa in vano e spessore del dente. Per poter ingranare correttamente, due ruote dentate devono avere lo stesso passo sulle primitive: il rapporto di trasmissione risulta allora inversamente proporzionale al rapporto tra il numero dei rispettivi denti:[16]
Il segno negativo o positivo indica rispettivamente la concordanza o discordanza del senso di rotazione della ruota condotta nei confronti di quella motrice.
Momento e rendimento[modifica | modifica wikitesto]
Poiché una serie di ingranaggi non è un amplificatore né un servosistema, la legge di conservazione dell'energia impone che la potenza in uscita dal sistema sia minore di quella entrante, per via delle perdite per attrito.
Perciò in caso di assenza di attrito la potenza entrante è uguale a quella uscente, il rendimento è unitario e il rapporto tra le velocità angolari degli ingranaggi (ingresso/uscita) è pari a quello dei momenti necessari ad azionarli (uscita/ingresso):
Tuttavia in generale ci sono perdite per attrito e il rendimento risulta inferiore a 1. Il rendimento meccanico di un sistema è pari al rapporto tra la potenza uscente e quella entrante , nel nostro caso e quindi in generale la coppia disponibile in uscita sarà più bassa di quella del caso ideale senza perdite:
- con
Data la presenza dell'attrito il momento motore sulle ruote 1 e 2 si calcola come segue. Detto il coefficiente d'attrito cinetico, la distanza tra il punto di contatto e il centro di istantanea rotazione e la forza scambiata fra i denti, si ha nella fase di recesso (fase finale del contatto tra denti):
Quindi, ricorrendo ai raggi primitivi , il rapporto di trasmissione dei momenti che dipende dal rendimento meccanico dell'ingranaggio vale:
e quindi (in recesso):
Questi risultati dipendono dall'attrito, dall'angolo di pressione e dai raggi .
Ciononostante, per fattori d'attrito bassi come nel caso di una corretta lubrificazione, si possono trascurarne i termini quadratici in :
- ~
- ~
- ~
Invece durante la fase di accesso (inizio contatto tra i denti) si ottiene:
e quindi (in accesso):
e quindi anche in questo caso
- ~
introducendo il valore dell'interasse si ottiene:
- ~
ove varia durante il contatto e occorre quindi assumere un valore medio.
Da questa approssimazione, ma anche dalla relazione esatta precedente, risulta chiaro come ad attrito basso, aumentando il numero dei denti e l'interasse (dimensioni globali) e aumentando l'angolo di pressione, il rapporto di trasmissione dei momenti tende al rapporto di trasmissione delle velocità, e le ruote dentate tendono a ruote di frizione, infatti:
- ∈ ~
Il rendimento non è costante su tutta la rotazione degli ingranaggi, nel caso degli ingranaggi cilindrici il massimo rendimento si ha dal passaggio dall'arco di accesso all'arco di recesso e corrisponde a 1, mentre è inferiore durante i due archi fino a un minimo di 0,75-0,83[17], il rendimento medio per questa categoria di trasmissioni è compreso tra 0,96 e 0,98.[18]
In modo più approssimativo il rendimento si può ricavare tramite la seguente formula ( rappresenta il numero dei denti per singolo ingranaggio):[19]
- =
Proporzionamento della dentatura[modifica | modifica wikitesto]
I denti, che sono superfici coniugate, cioè superfici continuamente a contatto durante l'ingranamento, si sviluppano in direzione radiale, a cavallo della superficie primitiva. Si definisce testa del dente la parte sporgente di questa, mentre la parte rientrante è chiamata base del dente. Ciascuna delle superfici laterali del dente è denominata profilo. Esso è suddiviso in due porzioni dalla circonferenza di primitiva: quella esterna a essa si chiama costa, quella posta all'interno si chiama fianco.
Si definisce profilo efficace la porzione del profilo che partecipa al contatto fra i denti dell'accoppiamento e costruito secondo le regole dei profili coniugati. Esso è compreso fra la circonferenza di troncatura interna e la circonferenza di troncatura esterna. Il dente è prolungato oltre la troncatura esterna fino alla circonferenza di testa, una smussatura che non partecipa al contatto e ha lo scopo di facilitare l'imbocco di una coppia di denti in presa, ed evitare rigature. Il dente si prolunga, inoltre, anche al di sotto della troncatura interna, con un raccordo fino alla circonferenza di piede, realizzato con profilo tale da evitare fenomeni di interferenza dell'accoppiamento.[20]
Il profilo di un dente può essere considerato diviso in due parti: si definisce addendum la distanza presa in direzione radiale fra la primitiva e la testa, quella cioè che, come abbiamo visto, delimita il dente superiormente; dedendum la distanza, anch'essa radiale, fra la primitiva e il piede, che delimita il dente inferiormente. La somma di queste due grandezze costituisce l'altezza del dente. Per costituire un accoppiamento, i denti di due ruote coniugate dovranno avere la stessa altezza, mentre queste due grandezze possono invece essere per esse differenti (questo vale per ruote esterne; per ruote interne l'addendum è interno alla primitiva, e il dedendum esterno a essa).[21]
I profili coniugati degli ingranaggi vengono tracciati con il metodo dell'epiciclo, dove una curva (epiciclo) viene fatta rotolare sulle circonferenze base dell'ingranaggio, nel suo rotolamento inviluppa il profilo del dente dell'ingranaggio, permettendo così la trasmissione del moto tramite spinta tra i profili coniugati e non per attrito tra essi.
Il numero minimo di denti da impiegare per ogni ingranaggio è influenzato da[17]:
- Continuità di trasmissione, che necessita un arco d'azione maggiore rispetto al passo e quindi il dente sia più lungo rispetto al suo passo.
- Evitare interferenza tra i profili, il dente non deve valicare oltre la base del dente dell'altra ruota dentata e quindi urti e blocchi la rotazione
Ruota cilindrica dritta[modifica | modifica wikitesto]

Il tipo più comune di ingranaggio è quello a denti dritti, che si possono considerare generati dalla protrusione di una sezione lungo un asse perpendicolare al piano stesso. La ruota dentata risulta perciò piatta, l'asse dei denti si proietta radialmente dal centro di rotazione dell'ingranaggio e le creste dei denti decorrono trasversalmente al piano di rotazione e parallelamente tra loro. Soffrono del problema del gioco:
quando la rotazione avviene in un senso, un dente spinge contro un lato del corrispondente dente dell'altra ruota; se la rotazione si inverte, la faccia opposta deve spingere sulla corrispondente e questo comporta un momento in cui i denti si spostano senza trasmettere movimento. Questo comporta che per un attimo dopo avere applicato rotazione in entrata non si ha rotazione in uscita.

La cremagliera (o dentiera) è una ruota cilindrica degenere, utilizzata in coppia con un'altra non degenere che avendo raggio minore del suo (che è considerabile infinito) fa sempre da pignone (o rocchetto): il sistema permette la conversione reciproca tra rotazione e traslazione. La velocità v con la quale la cremagliera trasla è infatti uguale a quella di un punto della primitiva della ruota dentata che la muove; inoltre i fianchi dei denti di una cremagliera sono costituiti da segmenti di retta inclinati, rispetto alla verticale di un angolo pari all'angolo di spinta, mentre i fianchi dei denti della ruota dentata sono a "evolvente".
Questo sistema è usato nelle automobili per convertire la rotazione dello sterzo in moto lineare laterale degli organi che agiscono sulle ruote e nella ferrovia a cremagliera, in cui i treni sono in grado di risalire forti pendenze grazie al contatto tra una ruota dentata sporgente sotto il locomotore e una lunga cremagliera solidale al binario, posta in mezzo alle rotaie dello stesso.
Ruota cilindrica elicoidale[modifica | modifica wikitesto]


La ruota elicoidale è un miglioramento rispetto a quella semplice. I denti sono tagliati con un certo angolo rispetto al piano, in modo che la superficie di spinta tra i denti sia maggiore e il contatto avvenga più dolcemente, eliminando lo stridore caratteristico degli ingranaggi semplici.
Lo svantaggio di questa soluzione è la produzione di una forza risultante lungo l'asse dell'ingranaggio, che deve essere sostenuta da un apposito cuscinetto a sfere. Un altro svantaggio è un maggiore attrito tra i denti causato dalla maggiore superficie di contatto, che deve essere ridotto con l'uso di lubrificanti (molto spesso, infatti, si trovano immersi in un bagno d'olio: come nel cambio)
Ruota cilindrica a doppia elica o bielicoidale (cuspide)[modifica | modifica wikitesto]

L'ingranaggio a doppia elica supera il problema precedentemente accennato grazie all'uso di denti con cresta a forma di V. Si può immaginare questo ingranaggio come costituito da due ruote elicoidali distinte affiancate specularmente, in modo che le forze assiali si annullino vicendevolmente.
Il simbolo della Citroën rappresenta appunto la V della ruota dentata a doppia elica, inventata da André Citroën.
Ruota cilindrica cicloidale[modifica | modifica wikitesto]

Questo tipo di ruota, conosciuta anche come "a linea d'imbocco circolare" è del tutto simile al bielicoidale, ma differisce da questo perché il profilo dei denti non è rettilineo, ma curvilineo.
Ingranaggi sghembi[modifica | modifica wikitesto]
L'ingranaggio sghembo elicoidale o ingranaggio elicoidale incrociato è una variante dell'ingranaggio elicoidale, dove viene progettando opportunamente l'angolo dei denti, in modo da accoppiare ingranaggi con gli assi sghembi o anche perpendicolari.
Questa disposizione configura una sensibile azione di scorrimento sulla superficie di contatto dei denti, riducendo la capacità di carico rispetto a un omologo ingranaggio elicoidale convenzionale, il che riduce il rendimento e generalmente può variare da circa il 90% fino al 25%. difatti il suo impiego è raro, in quanto il contatto puntiforme limita l'impiego nei casi in cui le forze in gioco siano modeste.
Risulta un sistema semplice ed economico per trasmettere potenza tra assi sghembi, con ampia possibilità di correzione nella disposizione assiale. Inoltre, anche con ingranaggi esterni, il senso di rotazione per l'ingranaggio condotto può essere opposto oppure lo stesso, a seconda dell'angolo scelto per l'elica.
Vite a evolvente[modifica | modifica wikitesto]


La "vite a evolvente" è una ruota cilindrica elicoidale con angolo d'elica molto grande, solitamente compreso tra 70° e 85°[22], e perciò ha un basso numero di denti, chiamati princìpi. Viene definita spesso vite senza fine perché la sua rotazione ha il solo scopo di essere trasmessa, come in tutte le ruote dentate. L'accoppiamento "vite senza fine-corona cilindrica elicoidale" ha lo scopo di trasferire moto e momento meccanico con elevato rapporto tra due assi perpendicolari non intersecantisi. Influiscono su questo rapporto l'inclinazione del filetto della vite e il numero dei denti (Z) della corona. La trasmissione del movimento è di norma dato dalla vite (ed è definita "conduttrice") e questo permette di mantenere una situazione statica all'uscita del sistema. Tuttavia esistono accoppiamenti dove la vite e la corona hanno un'inclinazione del filetto e dei denti (Z) tale da permettere la reversibilità. Vale a dire la possibilità di avere anche la corona dentata come "conduttrice", in grado cioè di trasmettere il movimento alla vite. Uno svantaggio di questo meccanismo è che ha rendimento <0,5, quindi per particolari angoli di elica, l'accoppiamento potrebbe risultare irreversibile, in parole povere: "la ruota non può muovere la vite". Il rendimento è basso perché si hanno molti strisciamenti e quindi c'è un'elevata usura, costringendo a regolare il dispositivo nel tempo. Per tale motivo i materiali utilizzati sono acciaio su bronzo.
Tipi di accoppiamenti[modifica | modifica wikitesto]


Gli accoppiamenti tra la vite e la corona possono essere di vario tipo, quali:
- Semplice; la vite e la corona sono di tipo cilindrico e il contatto tra i due è del tipo puntiforme
- A gola; la vite è di tipo cilindrico, mentre la corona è scavata al centro, in modo da avvolgere/avviluppare la vite, permettendo così un contatto lineare e quindi su una superficie maggiore.
In rari casi è la vite a essere scavata al centro - Globoidale; sia la vite sia la corona sono conformate in modo da essere scavate nel punto di contatto, in modo da avvilupparsi reciprocamente e avere più punti di contatto lineari ed estendere ulteriormente la zona di contatto.
Ruote coniche[modifica | modifica wikitesto]

Nelle ruote coniche la corona della ruota è smussata e le creste dei denti giacciono sulla superficie di un cono ideale. In questo modo due ingranaggi possono essere affiancati con un certo angolo tra gli assi. Se l'inclinazione dei denti di ciascuna ruota è di 45°, l'angolo tra gli assi è di 90°. Questo sistema è usato per esempio tra planetari e satelliti nel differenziale delle automobili.
Ruote coniche a dentatura a spirale o ipoide[modifica | modifica wikitesto]

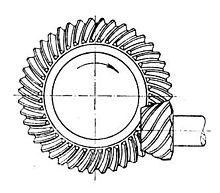
La dentatura a spirale è un particolare ingranaggio conico in cui i denti sono ruotati fino a diventare paralleli al piano di rotazione della ruota. Si ingrana con un pignone a denti elicoidali di piccole dimensioni, questa soluzione è utilizzata nella smerigliatrice angolare.
Una variante di questo sistema è usata in diversi sistemi di scappamento per orologi meccanici.
Un'altra variante, la dentatura ipoide, è formata da una corona e un pignone (con denti a spirale) i cui assi non giacciono sullo stesso piano (non s'intersecano). Per questo motivo l'angolo medio della spirale della corona è molto inferiore a quello del pignone. Tale coppia conica è stata introdotta nel campo dell'autotrazione per molti pregi: è più silenziosa, trasmette più momento meccanico avendo più ricoprimento tra i denti di entrambi i membri, permette di ridurre l'altezza del tunnel dove corre l'albero di trasmissione del moto dal motore anteriore al ponte posteriore aumentando l'abitabilità del mezzo, aumentando nel contempo la luce tra il terreno e la scatola del differenziale.
Ruote coniche a dentatura Zerol[modifica | modifica wikitesto]

Sistema previsto dalla normativa ISO 23509:2016, che definisce tale sistema come una variante della dentata a spirale, dove i denti di hanno angolo di spirale pari a zero (solitamente un ingranaggio con dente a spirale viene definito Zerol quanto l'angolo d'elica è minore di 10°), presentando per questo un'inclinazione/direzione identica ai sistemi con denti dritti, ma conservando una leggera curvatura del profilo del dente, esattamente come nei sistemi a spirale.
Posseggono le stesse caratteristiche delle ruote a denti elicoidali per ciò che riguarda carico sui cuscinetti, montaggio e manifattura.[23]
Ingranaggi non circolari[modifica | modifica wikitesto]

Gli ingranaggi non circolari sono ingranaggi speciali appositamente progettati per particolari impieghi. Mentre in un ingranaggio normale si cerca di massimizzare la trasmissione di energia con un rapporto costante, in un ingranaggio non circolare l'obiettivo è di avere un rapporto di trasmissione variabile durante la rotazione oppure lo spostamento dell'asse o altre funzioni. La sagoma dell'ingranaggio può essere di qualunque forma adatta allo scopo, limitatamente all'immaginazione dell'inventore o dell'ingegnere. Ruote con minime variazioni di rapporto possono avere forma quasi circolare, oppure l'asse può non corrispondere con il centro geometrico della ruota.
Normalmente sono usati per questi ingranaggi i denti paralleli, a causa in particolare della complicazione del moto. La fabbricazione non avviene come per i normali ingranaggi per fresatura, ma in genere per fusione, sinterizzazione o taglio da una lastra (al plasma o laser).
L'impiego si ha in particolare in macchine tessili e cambi automatici.
Sistemi epicicloidali[modifica | modifica wikitesto]

Quando almeno uno degli assi delle ruote non è fisso, a differenza del caso dei rotismi ordinari, si ha un rotismo epicicloidale.
I treni di ingranaggi epicicloidali o a planetario e satelliti costituiscono un sistema di uno o più ingranaggi chiamati satelliti, montati su un organo porta-satelliti chiamato portatreno (o anche planetario), che ruotano intorno a un pignone centrale anche detto solare; il tutto è posto all'interno di una ruota dentata internamente detta corona. L'asse di rotazione del portatreno e del solare coincidono. Uno di questi elementi è mantenuto fisso, un altro costituisce l'ingresso e il terzo l'uscita. Il rapporto di trasmissione è determinato dal numero dei denti ma anche da quale elemento è fisso, e questo è sfruttato in alcuni tipi di cambi di velocità. Il nome deriva dal fatto che il movimento degli ingranaggi satelliti è simile a quello che si supponeva avessero i pianeti del sistema solare nel sistema tolemaico, in cui si ipotizzava l'esistenza di moti detti epicicli.
Il rendimento del sistema epicicloidale con il portatreno bloccato varia molto a seconda del rapporto di trasmissione.[24]
Esempio[modifica | modifica wikitesto]

Un caso si ha quando il portatreno (in verde nell'illustrazione a lato) è fermo/bloccato e il pignone (giallo) costituisce l'ingresso/motrice, mentre i satelliti (blu) ruotano con un rapporto determinato dal numero di denti in ogni ruota. Se il pignone ha S denti (Solare) e ogni satellite P denti (Portatreno), il rapporto è uguale a -S/P. Nell'illustrazione il rapporto è -24/16 ovvero -3/2: ogni rotazione del pignone S produce una rotazione e mezza dei satelliti in direzione opposta. Se all'esterno viene applicata una corona con C denti, questa ruoterà P/C volte la rotazione dei satelliti. Poiché la rotazione dei satelliti è -S/P la rotazione del pignone, ne consegue che il rapporto tra corona e pignone è pari a: -S/C.
Un'altra possibilità è che la corona sia fissa, con l'ingresso applicato al portatreno (planetario) e l'uscita sul pignone. Questa configurazione produce un incremento di velocità con rapporto S/(S + C) cioè pignone/(corona + pignone).
Se invece è mantenuta ferma la corona e applicato l'ingresso al pignone, il portatreno (planetario) costituisce l'uscita, e il rapporto è (S + C)/S cioè (corona + pignone)/pignone. Questo è il massimo rapporto ottenibile da un sistema epicicloidale, ed è spesso usato in trattori e macchine edili per fornire un momento meccanico molto elevato alle ruote.
Diverse unità epicicloidali possono essere collegate in serie, con ogni planetario solidale con il pignone successivo (tranne ovviamente il primo e l'ultimo elemento). Si realizza così un gruppo motoriduttore (in diminuzione o in aumento) compatto, con rapporti molto elevati e con gli alberi di ingresso e uscita allineati.
Un sistema di cambio di velocità epicicloidale è utilizzato in alcune biciclette al posto del più comune cambio a deragliamento.
Casi[modifica | modifica wikitesto]
- Solare fisso, si hanno i rapporti di riduzione più vicini a 1
- Corona/anello fissa, si hanno i rapporti di riduzione più distanti da 1
- Portatreno fisso, si ha il caso di un rotismo ordinario e l'inversione del moto con un rapporto di riduzione leggermente meno accentuato rispetto al sistema con corona/anello fissa.
Modulo[modifica | modifica wikitesto]
Il modulo m di una ruota dentata viene definito come il rapporto tra il diametro primitivo 2R e il numero di denti z:
ed è il parametro su cui si basa il dimensionamento dei denti della ruota stessa.
Il passo della ruota è la distanza tra due profili omologhi consecutivi misurata lungo la primitiva. Esso è conseguentemente funzione del modulo e si esprime come:
Generalmente, dal modulo dipende l'altezza del dente, il quale presenta un'altezza totale pari a h = 2,25 m, così suddivisa:
- addendum
- dedendum
Questo tipo di proporzionamento è detto modulare.
Il numero di modulo è generalmente standardizzato e unificato tramite la UNI - 6586 (espresso in mm)[25][26]
| Categoria | Valori |
|---|---|
| Principali | 0,5-1-1,25-1,5-2-2,5-3-4-5-6-8-10-12-16-20-25-32-40-50 |
| Secondari | 0,75-1,125-1,375-1,75-2,25-2,75-3,25-3,5-3,75-4,5-5,5-6,5-7-9-11-14-18-22-28-36-45 |
Danni[modifica | modifica wikitesto]


Gli ingranaggi possono subire diversi danni:[27]
- Ruggine: si genera con l'avanzare del tempo e il non utilizzo, ed è accentuata in caso d'esposizione all'aria o all'acqua.
- Fatica: causata dalle sollecitazioni cicliche a cui sono sottoposti i denti, che causano un accumulo di danno nel tempo.
- Usura: si ha con il normale utilizzo ed è accelerata se si lavora senza lubrificanti.
- Ammaccatura o deformazione plastica: l'ingranaggio ha uno o più denti leggermente deformati per un carico eccessivo.
- Frattura dei denti: l'ingranaggio ha uno o più denti in meno, saltati per difetti di produzione, per un eccessivo carico, più spesso per sollecitazione a fatica.
Utilizzo[modifica | modifica wikitesto]
Gli ingranaggi sono utilizzati per il trasporto dell'energia e per modificare il rapporto di trasmissione. Una ruota cilindrica dritta appare inoltre sull'emblema della Repubblica Italiana come simbolo del lavoro su cui si basa la Repubblica.
Materiali e specifiche[28][modifica | modifica wikitesto]
I materiali utilizzati per le ruote dentate di varia natura sono molto variabili, a seconda del tipo di carico e ambiente a cui devono essere applicato; si va dalla plastica dei giocattoli e al PTFE (Teflon) ai metalli più resistenti.
Nelle applicazioni più gravose e industriali le specifiche necessarie sono:
- Elevata resistenza all'usura e alla fatica hertziana (pitting)
- Elevata resistenza alla fatica per flessione alla base dei denti
- Elevata resistenza all'urto
- Buona lavorabilità per asportazione di truciolo
- Attitudine ai trattamenti termici superficiali
Per tale motivo le famiglie di acciai più comunemente utilizzati sono:
- Acciai da cementazione
- Acciai per tempra superficiale
- Acciai da nitrurazione.
Note[modifica | modifica wikitesto]
- ^ (EN) Functioning 'mechanical gears' seen in nature for the first time
- ^ Derek J. de Solla Price, Sull'Origine degli Orologi Meccanici, Dispositivi a Moto Perpetuo e la Bussola, p.84
- ^ Progetto di Ricerca sul Meccanismo di Anticitera: Perché è così importante?, su antikythera-mechanism.gr. URL consultato il 10 gennaio 2011 (archiviato dall'url originale il 4 maggio 2012).«Si ritiene che il Meccanismo risalga al periodo tra il 150 e il 100 a.C.»
- ^ Norton, 2004, p. 462.
- ^ M. J. T. Lewis, Ingranaggi nel Mondo Antico, in Endeavour, vol. 17, n. 3, 1993, pp. 110–115, DOI:10.1016/0160-9327(93)90099-O.
- ^ a b (EN) Quadrante verticale | Museo Britannico, su Il Museo Britannico. URL consultato il 5 giugno 2022.
- ^ a b Irfan Habib, Storia Economica dell'India Medievale, 1200-1500, pagina 53, Pearson Education.
- ^ Joseph Needham (1986). Scienza e Civiltà in Cina: Volume 4, Parte 2, pagina 298. Taipei: Caves Books, Ltd.
- ^ Astrarium di Giovanni Dondi dell'Orologio, 1364 | cabinet, su cabinet.ox.ac.uk. URL consultato il 5 giugno 2022.
- ^ Astrolabe Di Muhammad Ibn Abi Bakr Al Isfahani, su mhs.ox.ac.uk.
- ^ Il Calendario Solare Portatile Bizantino: Il Secondo Meccanismo a Ingranaggi più Antico Esistente, su thearchaeologist.org. URL consultato il 5 giugno 2022.
- ^ Stromberg, Joseph, valvoline transmission fluid change, su autooilandfluid.com, Motion System Design. URL consultato il 28 agosto 2009.
- ^ (EN) Owen Jarus, Il primo computer del mondo, il Meccanismo di Anticitera, è stato "avviato" nel 178 a.C., affermano gli scienziati, su livescience.com, 14 aprile 2022. URL consultato il 5 giugno 2022.
- ^ (EN) Tony Freeth, Una Macchina da Calcolo Astronomica dell'Antica Grecia Rivela Nuovi Segreti, su Scientific American. URL consultato il 5 giugno 2022.
- ^ ingranaggi
- ^ Ardh uino, p. 577.
- ^ a b Trasmissioni ad ingranaggi (PDF), su www00.unibg.it. URL consultato il 9 gennaio 2018 (archiviato dall'url originale il 10 gennaio 2018).
- ^ Confronto fra meccanismi a rapporto di trasmissione costante (PDF), su web.inge.unige.it.
- ^ Rendimento di ruote dentate
- ^ Giovannozzi, p. 5.
- ^ G. Jacazio, p. 77.
- ^ Funaioli, Maggiore, Meneghetti, Meccanica applicata alle macchine, vol. I p. 226.
- ^ SO23509:2016(E) - Bevel and hypoid gear geometry. Standard, International Organization for Standardization, Geneva, CH, November 2016.
- ^ Meccanismi per trasmissione (organi di trasmissione) pag 159
- ^ Progettazione e modellazione parametrica di riduttori meccanici pag.13
- ^ Moduli UNI 6586-69
- ^ PRINCIPALI CAUSE DEL DANNEGGIAMENTO DEGLI INGRANAGGI (PDF), su aqm.it (archiviato dall'url originale il 4 marzo 2016).
- ^ Copia archiviata (PDF), su mdm.unifi.it. URL consultato il 10 giugno 2017 (archiviato dall'url originale il 17 maggio 2017).
Bibliografia[modifica | modifica wikitesto]
- Gianni Arduino, Renata Moggi, Educazione tecnica, 1ª ed., Lattes, 1990.
- R. Giovannozzi, Costruzione di macchine, Vol. 2, Pàtron Editore, 1965.
- G. Jacazio, B. Piombo, Meccanica applicata alle macchine, Vol. 2, Levrotto & Bella Editore, 1992.
Voci correlate[modifica | modifica wikitesto]
- Camma
- Cremagliera
- Corona (meccanica)
- Demoltiplica
- Errore di trasmissione
- Momento meccanico
- Pignone (meccanica)
- Rapporto di trasmissione
- Ruota dentata
- Riduttore di velocità
Altri progetti[modifica | modifica wikitesto]
 Wikiquote contiene citazioni sull'ingranaggio
Wikiquote contiene citazioni sull'ingranaggio Wikizionario contiene il lemma di dizionario «ingranaggio»
Wikizionario contiene il lemma di dizionario «ingranaggio» Wikimedia Commons contiene immagini o altri file sull'ingranaggio
Wikimedia Commons contiene immagini o altri file sull'ingranaggio
Collegamenti esterni[modifica | modifica wikitesto]
- ingranàggio, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- (EN) gear, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- Meccanismi (PDF), su web.inge.unige.it.
- Introduzione alle ruote dentate (PDF), su unibg.it.
- le ruote dentate (PDF), su nazzarenocorigliano.interfree.it. URL consultato il 3 gennaio 2010 (archiviato dall'url originale il 29 dicembre 2009).
- Generazione per inviluppo di ruote dentate a evolvente, Massimo Guiggiani (PDF), su dimnp.unipi.it.
- Teoria sulle ruote dentate, su valentiniweb.com.
- Ingranaggio, in Treccani.it – Enciclopedie on line, Roma, Istituto dell'Enciclopedia Italiana.
- Ingranaggi epicicloidali
| Controllo di autorità | Thesaurus BNCF 22354 · LCCN (EN) sh85053623 · GND (DE) 4067333-9 · BNF (FR) cb11978025k (data) · J9U (EN, HE) 987007560570205171 · NDL (EN, JA) 00562765 |
|---|













































