Metodo degli elementi finiti
Il metodo degli elementi finiti (FEM, dall'inglese Finite Element Method) è una tecnica numerica atta a cercare soluzioni approssimate di problemi descritti da equazioni differenziali alle derivate parziali riducendo queste ultime a un sistema di equazioni algebriche.
Benché esso competa in alcuni ambiti limitati con altre strategie numeriche (metodo delle differenze finite, metodo dei volumi finiti, metodo degli elementi al contorno, metodo delle celle, metodo spettrale, etc.), il FEM mantiene una posizione dominante nel panorama delle tecniche numeriche di approssimazione e rappresenta il kernel di gran parte dei codici di analisi automatici disponibili in commercio soprattutto in ambito strutturale e termo-strutturale, essendo di limitato utilizzo nelle applicazioni CFD a causa della instabilità dei solutori a numeri di Reynolds relativamente elevati.
Il metodo agli elementi finiti si presta molto bene a risolvere equazioni alle derivate parziali in geometrie come il telaio di un'automobile o il motore di un aereo, quando il dominio è variabile (per esempio una reazione a stato solido con condizioni al contorno variabili), quando l'accuratezza richiesta alla soluzione non è omogenea sul dominio (in un crash test su un autoveicolo, l'accuratezza richiesta è maggiore in prossimità della zona di impatto) e quando la soluzione cercata manca di regolarità.
Storia[modifica | modifica wikitesto]
Il metodo degli elementi finiti trova origini nelle necessità di risoluzione di problemi complessi di analisi elastica e strutturale nel campo dell'ingegneria civile ed aeronautica.[1] I primordi del metodo possono essere fatti risalire agli anni 1930-35 con i lavori di A. R. Collar e W. J. Duncan,[2] che introducono una forma primitiva di elemento strutturale nella risoluzione di un problema di aeroelasticità, e agli anni 1940-41 con i lavori di Alexander Hrennikoff e Richard Courant, dove entrambi, benché in differenti approcci, condividevano l'idea di suddividere il dominio del problema in sottodomini di forma semplice (gli elementi finiti).[3]
Tuttavia la nascita vera e propria e lo sviluppo del metodo agli elementi finiti si colloca nella seconda metà degli anni '50 con il contributo fondamentale di M. J. (Jon) Turner della Boeing, che formulò e perfezionò il Direct Stiffness Method, il primo approccio agli elementi finiti nel campo del continuo. Il lavoro di Turner trovò diffusione fuori dagli stretti ambiti dell'ingegneria aerospaziale, ed in particolare nell'ingegneria civile, tramite il lavoro di John Argyris presso l'Università di Stoccarda (che negli stessi anni aveva proposto una unificazione formale del metodo delle forze e del metodo degli spostamenti sistematizzando il concetto di assemblaggio delle relazioni di un sistema strutturale a partire dalle relazioni degli elementi componenti), e di Ray W. Clough presso l'Università di Berkeley[4] (che parlò per primo di FEM e la cui collaborazione con Turner aveva dato vita al celebre lavoro,[5] considerato come l'inizio del moderno FEM).
Altri contributi fondamentali alla storia dei FEM sono quelli di B. M. Irons, cui sono dovuti gli elementi isoparametrici, il concetto di funzione di forma, il patch test ed il frontal solver (un algoritmo per la risoluzione del sistema algebrico lineare), di R. J. Melosh, che inquadrò il FEM nella classe dei metodi Rayleigh-Ritz e sistematizzò la sua formulazione variazionale (una rigorosa e famosa esposizione della basi matematiche del metodo fu anche fornita nel 1973 da Strang e Fix[6]) e di E. L.Wilson, che sviluppo il primo (e largamente imitato) software FEM open source che diede genesi al SAP.[7]
Nel 1967 Zienkiewicz pubblicò il primo libro sugli elementi finiti. A partire dagli anni '70, il FEM ha trovato diffusione come strategia di modellazione numerica di sistemi fisici in un'ampia varietà di discipline ingegneristiche, per esempio elettromagnetismo,[8][9] fluidodinamica, calcolo strutturale e geotecnica. Sempre negli anni nacquero gran parte dei codici di analisi FEM commerciali (NASTRAN, ADINA, ANSYS, ABAQUS, SAMCEF, MESHPARTS, etc) tuttora disponibili.
Funzionamento[modifica | modifica wikitesto]
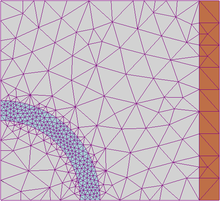
Il metodo F.E.M. si applica a corpi fisici suscettibili di essere discretizzati in domini di forme geometriche semplici. Nel continuo, ogni singolo elemento finito viene considerato un campo di integrazione numerica di caratteristiche omogenee.
La caratteristica principale del metodo degli elementi finiti è la discretizzazione attraverso la creazione di una griglia (mesh) composta da primitive (elementi finiti) di forma codificata (triangoli e quadrilateri per domini 2D, tetraedri e esaedri per domini 3D). Su ciascun elemento caratterizzato da questa forma elementare, la soluzione del problema è assunta essere espressa dalla combinazione lineare di funzioni dette funzioni di base o funzioni di forma.
L'esempio tipico è quello che fa riferimento a funzioni polinomiali, sicché la soluzione complessiva del problema viene approssimata con una funzione polinomiale a pezzi. Il numero di coefficienti che identifica la soluzione su ogni elemento è dunque legato al grado del polinomio scelto. Questo, a sua volta, governa l'accuratezza della soluzione numerica trovata.
Nella sua forma originaria, e tuttora più diffusa, il metodo agli elementi finiti viene utilizzato per risolvere problemi poggianti su leggi costitutive di tipo lineare. Tipici i problemi di sforzi - deformazioni in campo elastico, la diffusione del calore all'interno di un corpo materiale. Alcune soluzioni più raffinate consentono di esplorare il comportamento dei materiali anche in campo fortemente non lineare, ipotizzando comportamenti di tipo plastico o visco-plastico. Inoltre, si considerano talora problematiche accoppiate, all'interno delle quali si possono risolvere simultaneamente diversi aspetti complementari riconducibili ciascuno per conto proprio ad un'analisi F.E.M. separata. Tipico in questo senso il problema geotecnico del comportamento di un dato terreno (ambito geomeccanico) in presenza di moti di filtrazione di falda (ambito idrogeologico).
Il metodo degli elementi finiti fa parte della classe del metodo di Galërkin, il cui punto di partenza è la cosiddetta formulazione debole di un problema differenziale. Questa formulazione, basata sul concetto di derivata nel senso delle distribuzioni, di integrale di Lebesgue e di media pesata (mediante opportune funzioni dette funzioni test), ha il grande pregio di richiedere alla soluzione caratteristiche di regolarità realistiche per (quasi) tutti i problemi ingegneristici ed è pertanto uno strumento descrittivo molto utile. I metodi di tipo Galërkin si basano sull'idea di approssimare la soluzione del problema scritto in forma debole mediante combinazione lineare di funzioni (le shape functions) elementari. I coefficienti di tale combinazione lineare (detti anche "gradi di libertà") diventano le incognite del problema algebrico ottenuto dalla discretizzazione. Gli elementi finiti si distinguono per la scelta di funzioni di base polinomiali a pezzi. Altri metodi di tipo Galërkin come i metodi spettrali usano funzioni di base diverse.
Fasi per arrivare al modello[modifica | modifica wikitesto]
Per arrivare al modello agli elementi finiti si seguono delle fasi fondamentali, ognuna delle quali comporta l'inserimento di errori nella soluzione finale:
- Modellazione. Questa fase è presente in tutti gli studi ingegneristici: si passa dal sistema fisico a un modello matematico, che astrae alcuni aspetti di interesse del sistema fisico, focalizzando l'attenzione su poche variabili aggregate di interesse e "filtrando" le rimanenti. Ad esempio nel calcolo del momento flettente di una trave non si prendono in considerazione le interazioni a livello molecolare. Il sistema fisico se complesso viene suddiviso in sottosistemi. Nel caso in esame non è necessario, oppure si può pensare che si tratti di una parte appartenente a un sistema più complesso, ad esempio di una nave o di un aeroplano. Il sottosistema verrà poi suddiviso in elementi finiti ai quali verrà applicato un modello matematico. A differenza delle trattazioni analitiche è sufficiente che il modello matematico scelto sia adeguato alle geometrie semplici degli elementi finiti. La scelta di un tipo di elemento in un programma software equivale a una scelta implicita del modello matematico che vi è alla base. L'errore che può portare l'utilizzo di un modello deve essere valutato con prove sperimentali, operazione in genere dispendiosa per tempo e risorse.
- Discretizzazione: in una simulazione per via numerica è necessario passare da un numero infinito di gradi di libertà (condizione propria del "continuum") a un numero finito (situazione propria della griglia). La discretizzazione, nello spazio o nel tempo, ha lo scopo di ottenere un modello discreto caratterizzato da un numero finito di gradi di libertà. Viene inserito un errore dato dalla discordanza con la soluzione esatta del modello matematico. Questo errore può essere valutato opportunamente se esiste un modello matematico adeguato all'intera struttura (quindi preferibile da utilizzare rispetto all'analisi FEM) e in assenza di errori numerici di calcolo, ciò può essere considerato vero utilizzando calcolatori elettronici.
Caratteristiche degli elementi[modifica | modifica wikitesto]
Ogni elemento è caratterizzato da:
- Dimensione: 1D, 2D, 3D.
- Nodi: punti precisi dell'elemento che ne individuano la geometria. Su ogni nodo dell'elemento viene associato il valore di un campo o gradiente che interessa l'intera struttura. Nel caso di elementi meccanici il campo è quello delle reazioni vincolari e degli spostamenti (displacements).
- Gradi di libertà: i possibili valori che possono assumere i campi o gradienti nei nodi, due nodi adiacenti hanno gli stessi valori.
- Forze sui nodi: forze esterne applicate sui nodi o l'effetto delle reazioni vincolari. Esiste una relazione di dualità tra forze e reazioni vincolari. Detto il vettore di forze esterne su un nodo ed il vettore di DOF (dall'inglese "Degree Of Freedom", gradi di libertà), si assume linearità tra e :
- dove prende il nome di matrice di rigidezza (stiffness matrix). Questa relazione individua la dualità tra forze esterne e spostamenti. Il prodotto scalare è associato al valore del lavoro compiuto dalle forze esterne. I termini forza, reazione vincolare e stiffness matrix, sono estesi oltre l'ambito delle strutture meccaniche in cui è nata l'analisi FEM.
- Proprietà costitutive: le proprietà dell'elemento e del suo comportamento. In seguito verrà definito un materiale isotropo con comportamento lineare elastico, definito un modulo di Young ed un coefficiente di Poisson.
- Soluzione di un sistema di equazioni, anche non lineari risolte per via numerica dall'elaboratore. Viene introdotto un errore numerico trascurabile nel caso di sistemi lineari come quello in analisi.
Tipologia di elementi finiti[modifica | modifica wikitesto]
Tutti i programmi che impiegano il metodo degli elementi finiti per l'analisi strutturale sono dotati di una libreria di elementi finiti (in campo elastico lineare ma anche in quello elasto-plastico) monodimensionali, bidimensionali e tridimensionali per facilitare la modellazione di una struttura reale.
I più comuni sono i seguenti.
- monodimensionali:
- asta o truss: elemento rettilineo a 2 nodi che ha rigidezza solo per le traslazioni e pertanto è atto a trasmettere solo forze assiali. Viene utilizzato di norma per la modellazione di strutture reticolari.
- trave o beam: elemento rettilineo a 2 nodi capace di trasferire ai nodi a cui è connesso rigidezze per tutti e 6 i gradi di libertà e pertanto atto a trasmettere tutte le tipologie di sollecitazioni (forze assiali e taglianti e momenti flettenti e torcenti). Viene utilizzato per la modellazione di strutture intelaiate. Alcuni programmi posseggono anche l'elemento trave su suolo elastico alla Winkler per modellazione di travi di fondazione su suolo elastico.
- molla o boundary o spring: elemento rettilineo a due nodi dotato di rigidezza assiale e/o rotazionale utilizzato per modellare vari tipi di vincolo elastico quali ad esempio gli spostamenti imposti;
- rigido o rigel: elemento rettilineo a 2 nodi infinitamente rigido usato per modellare un legame infinitamente rigido tra due elementi finiti;
- bidimensionali:
- lastra o stress plane: elemento piano a 3 o 4 nodi per stati di sforzo piano che possiede solo due gradi di libertà per nodo corrispondenti alle traslazioni nel suo piano (rigidezza membranale) e pertanto atto a trasmettere solo gli sforzi lungo il suo piano. Non trasferisce alcuna rigidezza per gli altri gradi di libertà. Usato per la modellazione di strutture caricate nel loro stesso piano;
- piastra: elemento piano a 3 o 4 nodi che possiede solo tre gradi di libertà per nodo corrispondenti alla traslazione perpendicolare al suo piano e alle rotazioni rispetto ai due assi giacenti nel piano (rigidezza flessionale), e pertanto atto a trasmettere solo lo sforzo tagliante e i 2 momenti flettenti. Non trasferisce alcuna rigidezza per gli altri gradi di libertà. Usato per la modellazione di strutture bidimensionali inflesse. Alcuni software possiedono anche l'elemento piastra su suolo alla Winkler utilizzato per la modellazione di platee di fondazione su suolo elastico;
- lastra-piastra o guscio o shell: elemento piano a 3 o 4 nodi costituito dalla sovrapposizione dell'elemento piastra e dell'elemento lastra e che pertanto è dotato sia di rigidezza flessionale che membranale.
- deformazione piana o plane strain: elemento piano a 3 o 4 nodi per stati di deformazione piana che possiede solo due gradi di libertà per nodo corrispondenti alle traslazioni nel suo piano. Non trasferisce alcuna rigidezza per gli altri gradi di libertà. È utilizzato per la modellazione di strutture nelle quali lo spessore è prevalente rispetto alle altre dimensioni e dove si può considera impedita la deformazione nello spessore e pertanto lo stato di deformazione si considera piano come nell'analisi delle sezioni di condotte o di muri di sostegno.
- assialsimmetrico: elemento piano a 3 o 4 nodi che rappresenta un settore di un radiante di una struttura a simmetria radiale. Questo elemento è impiegato per modellare strutture solide ottenute per rotazione delle quali si frutta la simmetria radiale per analizzare solo un settore della struttura dell'ampiezza di un radiante. Ogni nodo ha 2 gradi di libertà corrispondenti alle traslazioni nel suo piano;
- tridimensionali:
- brick o elemento solido: elemento da 4 a 27 nodi che possiede solo tre gradi di libertà per nodo corrispondenti alla tre traslazioni. Non trasferisce alcuna rigidezza per gli altri gradi di libertà. È un elemento finito in grado di modellare elementi strutturali solidi nei quali cioè non vi sia una dimensione trascurabile rispetto alle altre. Questo elemento è in grado di interpretare uno stato tensionale tridimensionale. Usato ad esempio per modellare la stratigrafia del suolo.
Nodi[modifica | modifica wikitesto]
La definizione della geometria del modello che idealizza la struttura reale viene effettuata piazzando dei nodi, o punti nodali, sulla struttura in corrispondenza di punti caratteristici.
Nel posizionare i nodi sulla struttura bisogna tenere presente alcune considerazioni:
- il numero dei nodi deve essere sufficiente a descrivere la geometria della struttura. Ad esempio in corrispondenza dell'innesto trave-pilastro, dei cambi di direzione, ecc.
- i nodi devono essere posizionati anche nei punti e sulle linee di discontinuità. Ad esempio dove cambiano le caratteristiche dei materiali, le caratteristiche delle sezioni, ecc.
- si possono posizionare dei nodi in punti non necessari per la definizione geometrica della struttura ma di cui si vogliono conoscere gli spostamenti e le sollecitazioni interne
- se il software non lo prevede si devono posizionare dei nodi in corrispondenza di punti in cui sono applicati carichi concentrati o masse nodali
- si devono mettere nodi in tutti i punti che si intendono vincolare
- nel caso di strutture bidimensionali (piastre, lastre, ecc.) la suddivisione (mesh) in elementi finiti bidimensionali deve essere sufficientemente fitta per cogliere le variazioni di sforzo o di spostamento nelle regioni importanti ai fini dell'analisi.
Formulazione unidimensionale per equazioni del secondo ordine[modifica | modifica wikitesto]
Sia data un'equazione differenziale alle derivate parziali nella forma:
ristretta al dominio e condizioni al contorno:
dove è un vettore contenente i punti di e è un vettore contenente i valori assunti dalla funzione in tali punti. Condizioni espresse in questa forma vengono anche dette di Dirichlet. È inoltre possibile fornire come condizioni al contorno il valore assunto dalla derivata prima della funzione e in tal caso si chiamano condizioni di Neumann.
Il metodo degli elementi finiti prevede la moltiplicazione di entrambi i membri per una funzione di test :
L'integrazione di entrambi i membri sul dominio porta a:
Sfruttando l'integrazione per parti è possibile espandere il primo termine:
quindi:
L'approssimazione agli elementi finiti è un'approssimazione di Galërkin e si esegue a questo punto discretizzando il dominio nello spazio che ammette una base per che generalmente è costituita da polinomi a tratti di grado poco elevato.
La discretizzazione del dominio nel caso monodimensionale si effettua dividendo in intervalli con e
Le funzioni sono generalmente espresse nella forma:
La formulazione debole prevede quindi la determinazione di tale che risulti verificata l'uguaglianza:
Data l'appartenenza di allo spazio con base , si può scrivere come:
Effettuando la sostituzione e raccogliendo, si ottiene:
Tale uguaglianza è esprimibile in forma matriciale come:
dove i termini delle matrici si esprimono come:
La risoluzione del sistema lineare permette la determinazione dei coefficienti . Tali coefficienti permettono la determinazione dell'approssimazione nello spazio discretizzato localizzata nel dominio richiesto.
Caso di coefficienti costanti e approssimazione al baricentro[modifica | modifica wikitesto]
In generale, la determinazione delle matrici di rigidezza e di carico richiede l'utilizzo di metodi di quadratura per il calcolo del valore degli integrali definiti. Caso speciale ed interessante è però quello in cui i coefficienti dell'equazione differenziale sono tutti costanti. In tal caso è possibile una risoluzione esatta e particolarmente efficiente dell'equazione differenziale. Assumendo infatti:
gli integrali che compongono gli elementi delle matrici diventano:
Sostituendo alle funzioni di forma il valore corretto è possibile trovare una formulazione esatta degli integrali come funzione di variabili scelte. Considerando un singolo elemento costituente il dominio, compreso tra i nodi e , con le definizioni date in precedenza delle funzioni si ottiene una matrice di rigidezza quadrata del tipo:
Tali matrici sono le uniche non nulle, data la forma della funzione . Esse vanno a costituire la matrice di rigidezza , che risulta quindi componibile a partire dalle matrici sopra definite.
Lo stesso procedimento si può attuare per la matrice dei carichi ottenendo:
Componendo le matrici degli elementi nel modo corretto si giunge alla forma finale del sistema lineare:
Tale semplice soluzione è possibile solo in caso di coefficienti costanti, come detto in precedenza. In caso di coefficienti non costanti è possibile accontentarsi di una soluzione molto approssimata ma computazionalmente semplice e veloce effettuando una approssimazione al baricentro delle funzioni, considerando cioè una media del valore delle funzioni agli estremi di ciascun elemento:
Tale approssimazione permette di sfruttare i risultati appena raggiunti anche in caso di coefficienti non costanti, al prezzo di una minore precisione.
Esempio unidimensionale[modifica | modifica wikitesto]
Un problema tipico, detto talvolta problema dell'equazione di Poisson, può essere trovare la funzione il cui laplaciano è uguale ad una funzione data. L'equazione di Poisson in uno spazio monodimensionale si scrive come segue:
con vari tipi di condizioni al bordo, fra cui ad esempio:
Le condizioni al contorno in generale si possono dividere in tre gruppi:
- Condizioni di Dirichlet: Condizione imposta sulla funzione (ordine 0).
- Condizioni di Neumann: Condizione imposta sulla derivata prima della funzione rispetto alla normale uscente al contorno (ordine 1).
- Condizioni di Robin: Condizione imposta sulla combinazione lineare del valore della funzione e della sua derivata (condizione mista).
Se ad esempio si fa riferimento alle condizioni di Dirichlet:
La forma variazionale del problema diventa trovare appartenente a un opportuno spazio funzionale di funzioni che si annullano al bordo tale che per ogni funzione nello stesso spazio funzionale si abbia:
L'approssimazione del metodo agli elementi si ottiene introducendo una suddivisione dell'intervallo in sotto-intervalli su ciascuno dei quali la soluzione verrà assunta essere polinomiale. Questo permette di scrivere la soluzione approssimata, indicata come , mediante combinazione lineare delle funzioni di base dello spazio delle funzioni polinomiali a pezzi, indicate come :
I coefficienti sono le incognite del problema discretizzato. Usando come funzioni test proprio le funzioni di base, si ottiene infatti un insieme di n equazioni:
Indicando con la matrice:
con il vettore di elementi e con il vettore di elementi:
Il problema algebrico da risolvere è dato semplicemente dal sistema lineare:
La matrice è detta "matrice di rigidezza".
Confronto con il metodo alle differenze finite[modifica | modifica wikitesto]
Il metodo delle differenze finite (FDM, dall'inglese Finite Difference Method) è un metodo alternativo per approssimare le soluzioni di equazioni differenziali alle derivate parziali. Le principali differenze tra i due metodi sono:
- La caratteristica più attraente degli elementi finiti è l'abilità di gestire geometrie complesse con relativa semplicità. Le differenze finite sono, nella loro forma base, ristrette alla gestione geometrie semplici, come rettangoli e alcune alterazioni non complesse.
- La metodologia degli elementi finiti è di più semplice implementazione nel caso di problemi di statica lineare.
- Esistono diversi modi per considerare le differenze finite un caso particolare dell'approccio agli elementi finiti. Per esempio la formulazione degli elementi finiti è identica alla formulazione delle differenze per l'equazione di Poisson se il problema è discretizzato usando una forma rettangolare con ogni rettangolo diviso in due triangoli.
- La qualità dell'approssimazione degli elementi finiti è maggiore del corrispettivo approccio alle differenze finite.
In generale, il metodo degli elementi finiti è il metodo di scelta per tutti i tipi di analisi per la meccanica strutturale (per esempio per calcolare la deformazione e le tensioni di corpi deformabili o la dinamica delle strutture). Nella fluidodinamica computazionale invece si utilizzano altri metodi come il metodo dei volumi finiti.
Il metodo di Galërkin[modifica | modifica wikitesto]
Il metodo di Galërkin consiste nell'uso delle stesse funzioni di forma utilizzate nell'approssimazione all'interno dei sotto-intervalli di cui sopra, come funzioni peso nel calcolo del residuo ai minimi quadrati applicato alla formulazione debole del problema strutturale.
Note[modifica | modifica wikitesto]
- ^ Phillippe G. Ciarlet, The Finite Element Method for Elliptic Problems, Amsterdam, North-Holland, 1978.
- ^ Felippa, Carlos A., A Historical Outline of Matrix Structural Analysis: A Play in Three Acts, in Computers & Structures (Volume 79, Issue 14, June 2001, Pages 1313-1324), giugno 2001.
- ^ Waterman, Pamela J., Meshing: the Critical Bridge, in Desktop Engineering Magazine, 1º agosto 2008. URL consultato il 19 ottobre 2008 (archiviato dall'url originale il 20 novembre 2008).
- ^ Ray W. Clough, Edward L. Wilson, Early Finite Element Research at Berkeley (PDF), su edwilson.org. URL consultato il 25 ottobre 2007.
- ^ M.J. Turner, R.W. Clough, H.C. Martin, and L.C. Topp, Stiffness and Deflection Analysis of Complex Structures, in Journal of the Aeronautical Sciences, vol. 23, 1956, pp. 805–82.
- ^ Gilbert Strang, George Fix, An Analysis of the Finite Element Method, Englewood Cliffs, Prentice-Hall, 1973, ISBN 9780130329462.
- ^ Carlos A. Felippa, Introduction to Finite Element Methods, Lecture Notes for the course Introduction to Finite Elements Methods at the Aerospace Engineering Sciences Department of the University of Colorado at Boulder., from 1976.
- ^ Carlo Lonati, Gian Carlo Macchi; Dalmazio Raveglia, Crosstallk in a PAM technique telephone switching network due the skin effect. Approach with the Finite Element Method, Conference on the Computation of Magnetic Fields - Proceedings; Laboratoire d'Elecrotechnique, Grenoble, 1978.
- ^ John Leonidas Volakis, Arindam Chatterjee, Leo C. Kempel, Finite element method for electromagnetics: antennas, microwave circuits, and scattering applications, in IEEE Wiley Press, 1998.
Bibliografia[modifica | modifica wikitesto]
- (EN) G. Allaire and A. Craig: Numerical Analysis and Optimization: An Introduction to Mathematical Modelling and Numerical Simulation
- (EN) K. J. Bathe: Numerical methods in finite element analysis, Prentice-Hall (1976).
- (EN) J. Chaskalovic, Finite Elements Methods for Engineering Sciences, Springer Verlag, (2008).
- (EN) O. C. Zienkiewicz, R. L. Taylor, J. Z. Zhu: The Finite Element Method: Its Basis and Fundamentals, Butterworth-Heinemann, (2005).
Voci correlate[modifica | modifica wikitesto]
- Analisi agli elementi finiti
- Drilling
- Metodo dei volumi finiti
- Metodo delle differenze finite
- Metodo delle celle
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su metodo degli elementi finiti
Wikimedia Commons contiene immagini o altri file su metodo degli elementi finiti
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) finite element method, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Metodo degli elementi finiti, su MathWorld, Wolfram Research.
- FEM analysis - Comunità virtuale per la simulazione e la modellazione numerica, su it.groups.yahoo.com. URL consultato il 3 maggio 2019 (archiviato dall'url originale il 17 febbraio 2013).
- Sezione italiana della NAFEMS "The International Association for the Engineering Analysis Community", su nafems.it.
- Consorzio TCN: Tecnologie per il Calcolo Numerico - Centro Superiore di Formazione, su consorziotcn.it.
- CISM - International Centre for Mechanical Sciences, Udine, su cism.it.
- What is FEA (Metodo degli elementi finiti), su knol.google.com. URL consultato il 3 maggio 2019 (archiviato dall'url originale l'11 gennaio 2012).
- Il metodo degli elementi finiti, su calcolostrutture.net.
| Controllo di autorità | Thesaurus BNCF 57806 · LCCN (EN) sh85048349 · GND (DE) 4017233-8 · BNF (FR) cb11938437v (data) · J9U (EN, HE) 987007531228805171 · NDL (EN, JA) 00574434 |
|---|






![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle \partial [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46703085a826cf62489896a9db43eff1505bfbd0)





![{\displaystyle \int _{a}^{b}{\frac {\partial v}{\partial x}}{\frac {\partial u}{\partial x}}\alpha (x)dx-\left[v(x)\alpha (x){\frac {\partial u}{\partial x}}\right]_{a}^{b}+\int _{a}^{b}v(x)\sigma (x)u(x)dx=\int _{a}^{b}v(x)f(x)dx,\quad \forall \,v(x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1086a35572eddc2ac3bcdb89fdb5611ae66c1571)
![{\displaystyle \int _{a}^{b}{\frac {\partial v}{\partial x}}{\frac {\partial u}{\partial x}}\alpha (x)dx+\int _{a}^{b}v(x)\sigma (x)u(x)dx=\int _{a}^{b}v(x)f(x)dx+\left[v(x)\alpha (x){\frac {\partial u}{\partial x}}\right]_{a}^{b},\quad \forall \,v(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4619cefc4789d73e8da9455e6755de995dcb5c67)



![{\displaystyle [x_{j-1},x_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dea882ebdfde832fe4bd726caeced96a4d644aa7)





![{\displaystyle \int _{a}^{b}{\frac {\partial \phi _{j}}{\partial x}}{\frac {\partial u_{h}}{\partial x}}\alpha (x)dx+\int _{a}^{b}\phi _{j}(x)\sigma (x)u_{h}(x)dx=\int _{a}^{b}\phi _{j}(x)f(x)dx+\left[\phi _{j}(x)\alpha (x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b},\quad \forall \,j=1,\dots ,m.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc83caf48558ada494e1b29875d297ef224ff1f8)



![{\displaystyle \sum _{i=1}^{m}U_{i}\left(\int _{a}^{b}{\frac {\partial \phi _{j}}{\partial x}}{\frac {\partial \phi _{i}}{\partial x}}\alpha (x)dx+\int _{a}^{b}\phi _{j}(x)\sigma (x)\phi _{i}(x)dx\right)=\int _{a}^{b}\phi _{j}(x)f(x)dx+\left[\phi _{j}(x)\alpha (x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b},\quad \forall \,j=1,\dots ,m.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dd54451032e1c25a9fc2020bae239840c7db9a8)
![{\displaystyle \left[{\begin{array}{cccc}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\vdots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mm}\end{array}}\right]\cdot \left[{\begin{array}{c}U_{1}\\U_{2}\\\vdots \\U_{m}\end{array}}\right]=\left[{\begin{array}{c}f_{1}\\f_{2}\\\vdots \\f_{m}\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cacc7a382e4c2f84ab9bb4e7c968b7982b933b60)

![{\displaystyle f_{j}=\int _{a}^{b}\phi _{j}(x)f(x)dx+\left[\phi _{j}(x)\alpha (x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/802f7f2b555e9b6d1cdc96a13afab870ebd6217c)



![{\displaystyle f_{i}=f\int _{a}^{b}\phi (x)dx+\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de95d3f795c3e82fbdf5773dada3a13c86f2ee5)





![{\displaystyle {\begin{aligned}A_{k}=\left\{a_{ij}\right\}_{i,j=k}^{k+1}&=\left\{\alpha \int _{x_{i}}^{x_{j}}{\frac {\partial \phi _{i}}{\partial x}}{\frac {\partial \phi _{j}}{\partial x}}dx+\sigma \int _{x_{i}}^{x_{j}}\phi _{i}(x)\phi _{j}(x)dx\right\}_{i,j=k}^{k+1}\\&=\left\{\alpha \int _{x_{i}}^{x_{j}}{\frac {1}{h_{k}^{2}}}dx+\sigma \int _{x_{i}}^{x_{j}}\left(1+{\frac {1}{h_{k}}}(x-x_{i})\right)\left(1+{\frac {1}{h_{k}}}(x-x_{j})\right)dx\right\}_{i,j=k}^{k+1}\\&={\frac {\alpha }{h_{k}}}\left[{\begin{array}{cc}1&-1\\-1&1\end{array}}\right]+{\frac {\sigma h_{k}}{6}}\left[{\begin{array}{cc}2&1\\1&2\end{array}}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e1958c952fd82ff869080e8a6a8ec24987680e8)


![{\displaystyle F_{k}={\frac {fh_{k}}{2}}\left[{\begin{array}{c}1\\1\end{array}}\right]+\left[{\begin{array}{c}\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}\\\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f4b68acfa1aa89837d93bf7d41f1c0a960830c)
![{\displaystyle \left[{\begin{array}{ccccc}{\frac {\alpha }{h_{1}}}+{\frac {2\sigma h_{1}}{6}}&-{\frac {\alpha }{h_{1}}}+{\frac {\sigma h_{1}}{6}}&0&\cdots &\cdots \\-{\frac {\alpha }{h_{1}}}+{\frac {\sigma h_{1}}{6}}&\left({\frac {\alpha }{h_{1}}}+{\frac {2\sigma h_{1}}{6}}\right)+\left({\frac {\sigma }{h_{2}}}+{\frac {2\sigma h_{2}}{6}}\right)&-{\frac {\alpha }{h_{2}}}+{\frac {\sigma h_{2}}{6}}&0&\cdots \\0&-{\frac {\alpha }{h_{2}}}+{\frac {\sigma h_{2}}{6}}&\cdots &\cdots &\cdots \\\cdots &0&\cdots &\cdots &\cdots \\\cdots &\cdots &\cdots &\cdots &\cdots \end{array}}\right]\cdot \left[{\begin{array}{c}U_{1}\\U_{2}\\\cdots \\\cdots \\U_{m}\end{array}}\right]=\left[{\begin{array}{c}{\frac {fh_{1}}{2}}+\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}\\{\frac {fh_{1}}{2}}+{\frac {fh_{2}}{2}}+2\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}\\\cdots \\{\frac {fh_{m}}{2}}+\alpha \left[\phi _{j}(x){\frac {\partial u_{h}}{\partial x}}\right]_{a}^{b}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77f14afd69106133444367d7af15a6986a5f05f8)















![{\displaystyle A=[a_{ij}]=\int \limits _{0}^{1}\varphi _{j}^{\prime }\varphi _{i}^{\prime }dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/700a2fe1ba3d3b025b0360afb37b49b00bd3b7b2)



