Simmetria molecolare

Simmetria tetraedrica caratteristica di molecole quali il metano

In chimica, la simmetria molecolare descrive la simmetria presente nelle molecole e la classificazione delle molecole in base alla loro stessa simmetria applicando la teoria dei gruppi. Oltre che trovare applicazione in strutturistica chimica, viene comunemente impiegata per prevedere proprietà chimiche come la chiralità o quelle derivanti dalla presenza di un momento di dipolo molecolare, e per prevedere le transizioni spettroscopiche permesse. Applicando gli stessi concetti di simmetria agli orbitali molecolari è possibile elaborare un approccio integrato con la trattazione quantomeccanica del legame chimico.

La simmetria molecolare può essere dimostrata dal punto pratico utilizzando tecniche quali la diffrazione dei raggi X e la spettroscopia.

Concetti di simmetria

Operazione di inversione attraverso un centro di simmetria (1)

Elementi di simmetria

Un elemento di simmetria è un punto, una retta, o un piano che descrivono una data simmetria di una molecola. Esistono 4 elementi di simmetria:

• Asse di simmetria n-ario o asse di rotazione n-ario: asse, simboleggiato C_n, intorno al quale viene effettuata una rotazione di 360°/n che lascia apparentemente inalterata la molecola. Una molecola può possedere più assi di simmetria n-ari: in questo caso l'asse principale rappresenta quello con n maggiore. Ad esempio l'ammoniaca possiede un asse C₃ (rotazione di 120°) mentre l'acqua ha un asse C₂ (rotazione di 180°); inoltre l'ammoniaca ha anche un asse C²₃ (rotazione di 240°).
• Piano speculare o piano di simmetria o piano mirror: piano, simboleggiato σ, attraverso il quale una riflessione mantiene inalterata una molecola. Esistono piani verticali (σ_v, che contengono l’asse di rotazione principale, ad esempio l'acqua ne possiede due), piani orizzontali (σ_h, perpendicolari all'asse di rotazione principale, ad esempio il benzene ne possiede uno), e piani diedrici (σ_d, bisecano gli angoli diedri tra due piani verticali).
• Centro di simmetria o centro di inversione: simboleggiato i, indica un punto intorno al quale la proiezione della molecola mantiene quest'ultima inalterata. N₂ e SF₆ possiedono un centro di simmetria, al contrario della molecola dell'acqua.
• Asse n-ario di rotazione impropria: simboleggiato S_n, rappresenta la combinazione di un asse di rotazione n-ario e di un piano di simmetria perpendicolare. Da notare che S₁ corrisponde all'elemento σ_h, mentre S₂ equivale a i.

Operazioni di simmetria

Un'operazione di simmetria è un'azione che lascia immutata una molecola. A un'operazione di simmetria è associato uno o più elementi di simmetria. Le principali sono:

• Identità: indicata con E, corrisponde a un'operazione unitaria. L'elemento di simmetria può essere considerato la molecola stessa; questa operazione è caratteristica di tutte le molecole.
• Rotazione n-aria: è l'operazione associata all'asse di rotazione n-ario.
• Riflessione: è l'operazione associata al piano di simmetria.
• Inversione: è l'operazione prodotta proiettando ciascun punto della molecola nella direzione opposta equidistante dal centro di inversione.
• Rotazione impropria: operazione composta ottenuta in seguito a una rotazione n-aria seguita da una riflessione perpendicolare all'asse di rotazione.

Soventemente le operazioni di simmetria sono indicate utilizzando simboli identici a quelli dei rispettivi elementi di simmetria.

Gruppi puntuali

Sulla base degli elementi di simmetria posseduti è possibile ascrivere una molecola a un particolare gruppo puntuale; in chimica la notazione comunemente utilizzata consiste nel sistema Schoenflies. Ad esempio un composto quale CHBrClF, caratterizzato dalla sola identità, appartiene al gruppo puntuale C₁. Il perossido di idrogeno, oltre all'identità, possiede anche un asse di rotazione binario e pertanto si colloca nel gruppo puntuale C₂. La molecola dell'acqua, con un asse di rotazione binario e due piani speculari verticali, appartiene al gruppo C_2v, mentre l'ammoniaca possiede un asse C₃ e 3σ_v per cui si colloca nel gruppo C_3v. Le molecole lineari come il monossido di carbonio o l'acido cloridrico appartengono invece al gruppo puntuale C_∞v; aumentando gli elementi di simmetria si passa a gruppi quali D_2h, D_3h, D_4h... fino a giungere al gruppo tetraedrico T_d (del quale fa parte ad esempio il metano), a quello ottaedrico O_h (vi appartengono molecole quali l'esafluoruro di zolfo) e a quello icosaedrico I_h caratteristico del fullerene C₆₀ e di una serie di composti del boro.

In generale, si procede alla determinazione di un gruppo puntuale ricorrendo a un diagramma di flusso in cui il primo passo consiste nel determinare se una molecola è lineare oppure no.

La seguente tabella contiene una lista dei gruppi puntuali con le molecole rappresentative. La descrizione della struttura comprende anche le forme comuni delle molecole basate sulla teoria VSEPR.

Gruppo puntuale	Operazioni di simmetria	Semplice descrizione di una tipica geometria	Esempio 1	Esempio 2	Esempio 3
C1	E	nessuna simmetria, chirale	Bromoclorofluorometano	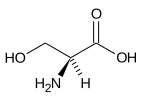Serina	D-glucopiranosio
Cs	E σh	piano di simmetria, nessun'altra simmetria	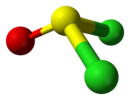Cloruro di tionile	Acido ipocloroso	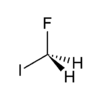Fluoroiodometano
Ci	E i	centro di inversione	(R,R) 1,2-dicloro-1,2-dibromoetano (conformero anti)
C∞v	E 2C∞ ∞σv	lineare	Acido fluoridrico	Ossido di diazoto
D∞h	E 2C∞ ∞σi i 2S∞ ∞C2	lineare con centro di inversione	Ossigeno	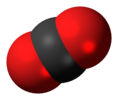Anidride carbonica
C2	E C2	"geometria a libro aperto", chirale	Perossido di idrogeno	Idrazina
C3	E C3	elica, chirale	Trifenilfosfina
C2h	E C2 i σh	planare con centro di inversione	trans-1,2-dicloroetilene
C3h	E C3 C32 σh S3 S35	elica	Acido borico
C2v	E C2 σv(xz) σv'(yz)	angolare (H2O) o "ad altalena" (SF4)	Acqua	Tetrafluoruro di zolfo	Fluoruro di solforile
C3v	E 2C3 3σv	piramidale trigonale	Ammoniaca	Ossicloruro di fosforo
C4v	E 2C4 C2 2σv 2σd	piramidale quadrata	Ossitetrafluoruro di xeno	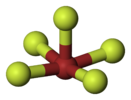Pentafluoruro di bromo
C6v	E 2C6 2C3 C2 3σv 3σd	piramidale esagonale	Benzene(esametilbenzene)cromo
D2	E C2(x) C2(y) C2(z)	"twist", chirale	Cicloesano (conformazione "twist")
D3	E C3(z) 3C2	tripla elica, chirale	Catione tris(etilendiammina)cobalto(III)
D2h	E C2(z) C2(y) C2(x) i σ(xy) σ(xz) σ(yz)	planare con centro di inversione	Etilene	Tetraossido di diazoto	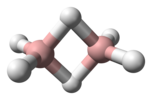Diborano
D3h	E 2C3 3C2 σh 2S3 3σv	planare trigonale o bipiramidale trigonale	Trifluoruro di boro	Pentacloruro di fosforo
D4h	E 2C4 C2 2C22C2 i 2S4 σh 2σv 2σd	planare quadrata	Tetrafluoruro di xeno	Anione octacloromolibdeno(III)
D5h	E 2C5 2C52 5C2 σh 2S5 2S53 5σv	pentagonale	Rutenocene	C70
D6h	E 2C6 2C3 C2 3C2' 3C2‘' i 2S3 2S6 σh 3σd 3σv	esagonale	Benzene	Dibenzenecromo
D8h	E 2C8 2C4 2C83 C2 4C2' 4C2‘' i 2S83 2S4 2S8 σh 4σd 4σv	ottagonale	Uranocene
D2d	E 2S4 C2 2C2' 2σd	"90° twist"	Propadiene	Tetranitruro di tetrazolfo
D3d	E C3 3C2 i 2S6 3σd	"60° twist"	Etano (rotamero sfalsato)	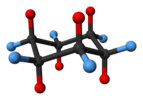Cicloesano (conformazione "a sedia")
D4d	E 2S8 2C4 2S83 C2 4C2' 4σd	"45° twist"	Decacarbonile di dimanganese (rotamero sfalsato)	Zolfo-α (rotamero sfalsato)
D5d	E 2C5 2C52 5C2 i 3S103 2S10 5σd	"36° twist"	Ferrocene (rotamero sfalsato)
D6d	E 2S12 2C6 2S4 2C3 2S125 C2 6C2' 6σd	"30° twist"	Dibenzenecromo (rotamero sfalsato)
S4	E S4 C2 S43	asse improprio S4	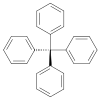Tetrafenilmetano	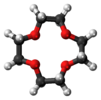12-corona-4	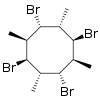1,3,5,7-tetrabromo-2,4,6,8-tetrametil-cicloottano
S6	E C3 C32 i S65 S6	asse improprio S6	[6,5]coronano	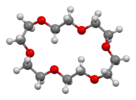18-corona-6
S8	E S8 C4 S83 C2 S85 C43 S87	asse improprio S8
S10	E C5 C52 C53 C54 i S107 S109 S10 S103	asse improprio S10
Td	E 8C3 3C2 6S4 6σd	tetraedrico	Metano	Anidride fosforica	Adamantano
Oh	E 8C3 6C2 6C4 3C2 i 6S4 8S6 3σh 6σd	ottaedrico o cubico	Cubano	Esafluoruro di zolfo	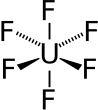Esafluoruro di uranio
Ih	E 12C5 12C52 20C3 15C2 i 12S10 12S103 20S6 15σ	icosaedrico o dodecaedrico	Buckminsterfullerene	Anione dei dodecaborani	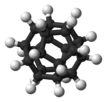Dodecaedrano

Tavole dei caratteri

Le tavole dei caratteri sono utilizzate per elencare sinteticamente il risultato delle operazioni di simmetria e i relativi tipi di simmetria caratteristici di uno specifico gruppo puntuale. Sono molto utili dal punto di vista pratico, ad esempio per determinare in modo relativamente agevole quali orbitali possono combinarsi in un legame chimico, considerando che si combinano gli orbitali che presentano medesima simmetria.

Per ricavare le tavole dei caratteri bisogna esprimere le operazioni di simmetria nella notazione matriciale. Dato un set base di partenza è possibile ottenere una cosiddetta matrice rappresentativa per ogni operazione di simmetria. Ad esempio partendo da un insieme di tre orbitali di valenza p (indicati come p_A, p_B e p_C), nel gruppo puntuale C_2v considerando un'operazione σ_v si ottiene l'insieme (p_A, p_C, p_B). In termini matriciali ciò equivale alla moltiplicazione

$\left(p_{A},p_{C},p_{B}\right)=\left(p_{A},p_{B},p_{C}\right){\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}}=\left(p_{A},p_{B},p_{C}\right)D\left(\sigma _{v}\right)$

dove D(σ_v) è la matrice rappresentativa. Se la trasformazione di base permette che tale matrice sia fattorizzabile in una matrice a blocchi diagonale, allora si è in presenza di una rappresentazione riducibile che per successive fattorizzazioni fornisce infine una rappresentazione monodimensionale irriducibile. I caratteri sono ottenuti proprio da queste rappresentazioni irriducibili.

Riassumendo quanto detto sopra, nel caso del gruppo puntuale C_2v qui considerato si perviene alla seguente tavola dei caratteri:

C2v	E	C2	σv	σv'	h=4
A1	1	1	1	1	z	x2, y2, z2
A2	1	1	−1	−1	Rz	xy
B1	1	−1	1	−1	x, Ry	xz
B2	1	−1	−1	1	y, Rx	yz

La prima colonna indica i tipi di simmetria: le lettere A e B indicano rappresentazioni monodimensionali; quando la rotazione intorno l'asse principale ha il carattere +1 si utilizza la lettera A, mentre quando ha il carattere −1 si utilizza la lettera B. A₁ indica la rappresentazione che possiede tutti caratteri con valore +1. Quando esistono rappresentazioni di ordine maggiore si utilizzano rispettivamente la lettera E nel caso di rappresentazioni bidimensionali e la lettera T per rappresentazioni tridimensionali. Da notare che gli orbitali che possiedono una data simmetria sono invece indicati con stesse lettere però in minuscolo. Le colonne successive elencano le operazioni di simmetria (riunite in classi) e i rispettivi caratteri delle rappresentazioni irriducibili: il carattere +1 indica la conservazione della simmetria, mentre il valore −1 indica l'antisimmetria. La colonna in cui compare h=4 indica nell'intestazione l'ordine del gruppo (il numero totale di operazioni di simmetria) e la base della rappresentazione irriducibile (orbitali p_x, p_y, p_z o la rotazione R attorno a un asse cartesiano). L'ultima colonna indica le basi analoghe per le funzioni di secondo grado (gli orbitali d).

Le tavole dei caratteri per ciascun gruppo puntuale sono raccolte in pubblicazioni scientifiche specialistiche.

Bibliografia

• D.F. Shriver, P.W Atkins; C.H. Langford, Chimica inorganica, Zanichelli, 1993, ISBN 978-88-08-12624-5.
• F.A. Cotton, Chemical Applications of Group Theory, Wiley-Interscience, 1990, ISBN 978-0-471-51094-9.

Collegamenti esterni

• (EN) Tavole dei caratteri dei gruppi puntuali, su webqc.org.