Fattorizzazione

In matematica, la fattorizzazione o scomposizione in fattori di un numero o altro oggetto matematico consiste nella loro rappresentazione come prodotto di più fattori, di solito più piccoli o più semplici e della stessa natura. Per esempio è una fattorizzazione dell'intero . Invece è una fattorizzazione del polinomio
La fattorizzazione non è generalmente considerata significativa negli insiemi numerici aventi un'operazione di divisione, come i numeri reali o quelli complessi, poiché qualsiasi può essere scritto banalmente come per ogni diverso da zero. In ogni caso un'utile fattorizzazione per i numeri razionali e le funzioni razionali può essere ottenuta riducendoli ai minimi termini e successivamente fattorizzando i loro numeratori e denominatori.
La fattorizzazione degli interi era già in uso presso gli antichi matematici greci: Apollonio di Perga, Archimede, Euclide, ecc. Si deve a Euclide il teorema fondamentale dell'aritmetica in cui si afferma che ogni intero positivo può essere scomposto in un prodotto di numeri primi, cioè numeri che non possono essere ulteriormente fattorizzati in altri interi maggiori di 1, e che questo prodotto è unico[1] se si trascura l'ordine dei fattori. La fattorizzazione è un processo algoritmico di successive divisioni per ottenere i singoli fattori e quindi può apparire metaforicamente come l'inverso della moltiplicazione, ma la difficoltà di questo processo cresce enormemente con i grandi numeri ed è proprio questa difficoltà che viene sfruttata dai moderni sistemi di crittografia RSA.
Anche la fattorizzazione di un polinomio è studiata da secoli. Nell'algebra elementare, fattorizzare un polinomio si riduce al problema di trovare le sue radici per poi trovare i fattori il cui prodotto è uguale al polinomio. Un polinomio con coefficienti interi gode anch'esso della proprietà simile a quella del teorema fondamentale dell'aritmetica, con la differenza che ogni suo fattore viene detto polinomio irriducibile. Un polinomio a una incognita e coefficienti complessi ammette un'unica fattorizzazione in prodotto di polinomi lineari (cioè di grado uno), caso particolare del teorema fondamentale dell'algebra. I polinomi a coefficienti interi sono fondamentali per l'algebra computazionale. Ci sono algoritmi computazionali efficienti per il calcolo completo di un anello polinomiale a coefficienti razionali (si veda la scomposizione dei polinomi).
Un anello commutativo che ha una fattorizzazione unica è detto dominio a fattorizzazione unica. Ci sono sistemi numerici come certi anelli di interi algebrici, che non sono domini a fattorizzazione unica. Tuttavia, essi soddisfano la proprietà più debole di essere un dominio di Dedekind: gli ideali ammettono fattorizzazione unica in ideali primi.
La fattorizzazione si può riferire a un concetto più generale di scomposizione di un oggetto matematico in un prodotto di oggetti più piccoli o più semplici. Per esempio, ogni funzione può essere fattorizzata nella composizione di una funzione suriettiva con una funzione iniettiva. Le matrici hanno molti tipi di fattorizzazione in prodotti di matrici. Per esempio, ogni matrice ha un'unica fattorizzazione LUP consistente nel prodotto di una matrice triangolare inferiore , avente tutti gli elementi della diagonale uguali a 1, per una matrice triangolare superiore , e per una matrice di permutazione .
Numeri interi[modifica | modifica wikitesto]
Dal teorema fondamentale dell'aritmetica si ha che ogni numero intero maggiore di 1 ha un'unica fattorizzazione in numeri primi, cioè in numeri interi che non possono essere a loro volta fattorizzati in interi maggiori dell'unità.
Per calcolare la fattorizzazione di un intero , occorre un algoritmo per trovare un divisore di a meno che sia primo. Nel caso che si sia trovato un divisore, la ripetizione dell'algoritmo ai fattori e / si concluderà alla fine con il completamento della fattorizzazione di .[2]
Per trovare un divisore di , se esiste, è sufficiente verificare tutti i valori di tali che e . Infatti, se è un divisore di e , allora è un divisore di tale che .
Se si provano i valori di in ordine crescente, il primo divisore trovato è necessariamente un numero primo, e il cofattore non può avere un divisore minore di . Per ottenere la completa fattorizzazione, è perciò sufficiente ripetere l'algoritmo cercando un divisore di non minore di e non maggiore di .
Non occorre verificare tutti i valori di per applicare il metodo. In linea di principio è sufficiente provare con divisori primi. Per fare ciò occorre avere una tabella di numeri primi, magari ottenuta con il crivello di Eratostene. Poiché il metodo di fattorizzazione indicato è essenzialmente lo stesso del crivello, è in generale più efficiente cercare un divisore solo per quei numeri per i quali non è immediatamente chiaro se siano primi o no. Normalmente si procede con i divisori 2,3,5 e i numeri , che abbiano come cifra delle unità 1,3,7,9 e che la somma delle cifre di non sia multipla di 3.
Questo metodo funziona bene per fattorizzare piccoli interi, ma è inefficiente per grandi interi. Ad esempio, Pierre de Fermat non fu in grado di scoprire che il sesto numero di Fermat
non è un primo. Infatti, l'applicazione del metodo riportato richiederebbe più di 10 000 divisioni, per quel numero di 10 cifre.
Ci sono algoritmi più efficienti, ma non ancora abbastanza. Allo stato attuale dell'arte non si riesce ancora a fattorizzare, pur con i calcolatori più potenti, un numero che abbia 500 cifre e sia il prodotto di due primi scelti a caso. Questa incapacità garantisce la sicurezza su cui si basa il sistema di crittografia RSA, che è largamente usato per la protezione delle comunicazioni internet.
Esempio[modifica | modifica wikitesto]
Per fattorizzare in un prodotto di primi:
- Iniziare con la divisione per 2 (n è pari) e . Continuare con 693, e 2 come primo candidato divisore.
- 693 è dispari (2 non è un suo divisore), ma è multiplo di 3: si ottiene e Continuare con 231, e 3 come primo candidato divisore.
- Anche 231 è multiplo di 3: si ottiene , e quindi Continuare con 77, e 3 come primo candidato divisore.
- 77 non è multiplo di 3, perché la somma delle cifre è 14 che non è multiplo di 3. Non è neanche multiplo di 5 perché la cifra delle unità è 7. Il prossimo divisore da cercare è perciò 7. Si ottiene e quindi Si verifica facilmente che 7 è primo. Continuare con 11, e 7 come primo candidato divisore.
- Siccome il processo è terminato. Perciò 11 è primo, e la fattorizzazione completa in primi risulta
Espressioni[modifica | modifica wikitesto]
La manipolazione delle espressioni è alla base dell'algebra. La fattorizzazione è uno dei più importanti metodi di manipolazione delle espressioni per diversi motivi. Se si riesce a rappresentare un'equazione in forma fattorizzata , il problema di risolvere l'equazione si suddivide in due problemi indipendenti (e di solito più facili): e . In una espressione fattorizzata, i fattori sono molto più semplici, e offrono quindi una migliore visione del problema. Per esempio:
che contiene 16 moltiplicazioni, 4 sottrazioni e 3 addizioni, può essere fattorizzata in un'espressione molto più semplice
con solo tre moltiplicazioni e tre sottrazioni. Inoltre la forma fattorizzata indica già quali sono le radici del polinomio.
La fattorizzazione non è sempre possibile, e quando lo è i fattori non sono sempre più semplici. Per esempio, può essere fattorizzato in due fattori irriducibili e
Sono stati sviluppati vari metodi per trovare le fattorizzazioni, alcuni sono descritti più avanti.
La risoluzione di equazioni algebriche può essere vista come un problema di fattorizzazione di polinomi. Infatti il teorema fondamentale dell'algebra può essere espresso come segue: ogni polinomio in di grado con coefficienti complessi può essere fattorizzato in fattori lineari con , dove gli sono le radici del polinomio.[3] Anche se la struttura della fattorizzazione è nota in questi casi, gli , in genere non possono essere calcolati in termini di radicali (cioè mediante radici -esime), per il teorema di Abel-Ruffini. In molti casi il meglio che si può fare è calcolare valori approssimati delle radici con appositi algoritmi.
Storia della fattorizzazione delle espressioni[modifica | modifica wikitesto]
L'uso sistematico di manipolazioni algebriche per semplificare le espressioni (più precisamente le equazioni) può essere datato dal secolo IX, con il testo Breve opera sul calcolo di spostare e raccogliere di al-Khwarizmi che è intitolato con due tipi di manipolazioni.[4]
Tuttavia, persino per le soluzioni delle equazioni di secondo grado, il metodo di fattorizzazione non era in uso prima del lavoro di Harriot pubblicato nel 1631, dieci anni dopo la sua morte.[5]
Nel suo libro Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, Harriot disegna tabelle per l'addizione, sottrazione, moltiplicazione e divisione di monomi, binomi e trinomi. Successivamente, in una seconda sezione, egli imposta l'equazione e mostra che essa ha la forma di una moltiplicazione precedentemente indicata, dando la sua fattorizzazione .[6]
Metodi generali[modifica | modifica wikitesto]
I seguenti metodi si applicano a qualsiasi espressione fatta di somme o che può essere trasformata in somme. Quindi essi sono applicati spesso ai polinomi, anche quando i termini delle somme non sono monomi, ma prodotti di variabili e costanti.
Fattori comuni[modifica | modifica wikitesto]
Può verificarsi il caso che tutti i termini della somma siano costituiti da prodotti e che alcuni fattori siano comuni a tutti i termini. In questo caso la proprietà distributiva permette il loro raccoglimento a fattor comune totale. Se ci sono diversi fattori comuni, conviene raccogliere a fattor comune il loro massimo comun divisore (MCD).
Per esempio,[7]
poiché 2 è l'MCD di 6, 8, 10, e divide tutti i termini.
Raggruppamento[modifica | modifica wikitesto]
Il raggruppamento di termini permette di usare altri metodi di fattorizzazione.
Ad esempio, per fattorizzare
si nota che i primi due termini hanno in comune il fattore , e gli ultimi due hanno in comune il fattore . Quindi
Poi risulta evidente il fattore in comune e quindi
In generale, questo metodo funziona per somme di quattro termini che sono il risultato del prodotto di due binomi. In qualche caso, non frequente, anche in esempi più complicati.
Addizione e sottrazione di termini[modifica | modifica wikitesto]
Qualche volta il raggruppamento di alcuni termini appare come parte di un prodotto notevole. In questo caso è utile aggiungere i termini mancanti e nello stesso tempo sottrarli per non alterare il valore dell'espressione. Un tipico uso è il metodo del completamento del quadrato per ottenere una forma quadratica.
Un altro esempio è la fattorizzazione di . Se si introduce l'unità immaginaria , comunemente denotata con , si ottiene una differenza di quadrati
Nel caso si volesse anche una fattorizzazione con coefficienti reali, si può aggiungere e sottrarre . Raggruppando tre termini si può riconoscere il quadrato di un binomio
Inoltre, sottraendo e aggiungendo si ottiene la fattorizzazione
Queste fattorizzazioni funzionano non solo con i numeri complessi, ma anche per ogni campo di numeri, ove uno dei valori -1, 2, -2 sia un quadrato. In un campo finito, il prodotto di due numeri, che non siano dei quadrati, è un quadrato; ciò implica che il polinomio , che è irriducibile nel campo degli interi, diventa riducibile modulo un primo. Per esempio,
- poiché
- poiché
- poiché
Prodotti notevoli[modifica | modifica wikitesto]
Molte identità rappresentano un'uguaglianza tra una somma e un prodotto. I precedenti metodi possono mettere in evidenza la parte somma di un'identità che quindi può essere sostituita con il suo prodotto.
Di seguito sono riportate identità in forma generalizzata (tramite le variabili e rappresentanti parti dell'espressione originale da fattorizzare).[8]

- Differenza tra due quadrati
- Per esempio,
- Somma/differenza di due cubi
- Differenza di due potenze di quarto grado
- Somma/differenza di due valori all'-esima potenza
- Nelle seguenti identità i fattori sono spesso a loro volta fattorizzabili.
- Differenza con esponente pari
- Differenza, con qualsiasi esponente
- Questo è un esempio di fattori più numerosi della somma da fattorizzare.
- Somma con esponente dispari
- (ottenuta scambiando con nella precedente formula)
- Somma con esponente pari
- Se l'esponente è una potenza di 2, l'espressione non può, in generale, essere fattorizzata senza usare numeri complessi (se e contengono numeri complessi potrebbe non essere vero). Se ha un divisore dispari, cioè se con dispari, si può
usare la formula precedente ("Somma con esponente dispari") e applicarla a
- Trinomi e formule cubiche
- Sviluppi binomiali
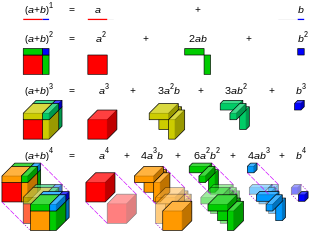
- Nel teorema binomiale ci sono delle forme facilmente riconoscibili in base ai numeri interi presenti di grado piccolo:
- In generale, i coefficienti degli sviluppi di e sono i coefficienti binomiali, che appaiono nella -esima riga del triangolo di Pascal.
Radici dell'unità[modifica | modifica wikitesto]
Le radici -esime dell'unità sono quei numeri complessi ciascuno dei quali è la radice del polinomio . Essi sono perciò i numeri
per
Dal cui segue che per ogni coppia di espressioni e , si ha:
Se ambedue sono espressioni reali, e si desiderano fattori reali, occorre rimpiazzare ogni coppia di fattori complessi coniugati con i suoi prodotti. Poiché il complesso coniugato di è e
si hanno le seguenti fattorizzazioni reali (si passa dall'una all'altra sostituendo con o con , e applicando le solite formule trigonometriche:
I coseni che appaiono in queste fattorizzazioni sono numeri algebrici, che possono essere espressi in termini di radicali (possibile in quanto il loro gruppo di Galois è ciclico); tuttavia, queste espressioni radicali sono troppo complicate da usare, con l'eccezione per piccoli valori di . Per esempio:
Spesso si desidera una fattorizzazione con coefficienti razionali. Esse implicano polinomi ciclotomici. Per ottenere fattorizzazioni razionali di somme e differenze o di potenze, è necessaria una notazione per l'omogeneizzazione di un polinomio: se , la sua omogeneizzazione è il polinomio a due variabili . Allora si ottiene
dove i prodotti si riferiscono a tutti i divisori di , o di che non sono divisori di , e è l'-esimo polinomio ciclotomico.
Per esempio:
poiché i divisori di 6 sono 1,2,3,6, e i divisori di 12 che non dividono 6 sono 4 e 12.
Polinomi[modifica | modifica wikitesto]
Per i polinomi la fattorizzazione è strettamente legata al problema della soluzione di una equazione algebrica. Un'equazione algebrica ha la forma
dove è un polinomio in con . Una soluzione di questa equazione (chiamata anche radice del polinomio) è un valore di tale che
Se è una fattorizzazione di come prodotto di due polinomi, allora le radici di sono l'unione delle radici di e quelle di . Per cui la soluzione di è ridotta ai più semplici problemi di risolvere e .
All'opposto, il teorema del fattore asserisce che se è una radice di , allora può essere fattorizzato come
dove è il quoziente di una divisione euclidea (vedi regola di Ruffini) di per il fattore lineare .
Se i coefficienti di sono reali o complessi, il teorema fondamentale dell'algebra afferma che ha una radice reale o complessa. Utilizzando ricorsivamente il teorema del fattore, risulta che
dove sono le radici reali o complesse di , con alcune di esse anche ripetute. Tale fattorizzazione completa è unica.
Se i coefficienti di sono reali, in generale si preferisce che anche la fattorizzazione abbia coefficienti reali. In questo caso, nella fattorizzazione completa possono esserci fattori quadratici. Questa fattorizzazione può facilmente essere dedotta dalla fattorizzazione completa precedente. Infatti, se è una radice non reale di , allora il suo complesso coniugato è anch'esso una radice di . Per cui, il prodotto
è un fattore di con coefficienti reali. Ripetendo l'operazione per tutti i fattori non reali si ottiene una fattorizzazione con fattori reali lineari o quadratici.
Per calcolare questi fattori, reali o complessi, occorre trovare le radici del polinomio, che possono non essere esatte, ma solo approssimate tramite algoritmi di calcolo delle radici.
In pratica, molte equazioni algebriche di interesse hanno coefficienti interi o razionali e si desidera lo stesso per la fattorizzazione. Il teorema fondamentale dell'aritmetica può essere generalizzato a questo caso, in quanto i polinomi con coefficienti interi o razionali hanno anch'essi la proprietà di avere un'unica fattorizzazione. Più precisamente, ogni polinomio con coefficienti razionali può essere fattorizzato nel prodotto
dove è un numero razionale e sono polinomi variabili a coefficienti interi che sono polinomi irriducibili e primitivi; ciò significa che nessuno dei può essere scritto come prodotto di due polinomi (con coefficienti interi) che non siano 1 o -1 (gli interi sono considerati come polinomi di grado zero). Inoltre, questa fattorizzazione è unica a meno dell'ordine e del segno dei fattori.
Ci sono efficienti algoritmi per calcolare le fattorizzazioni, utilizzati dalla maggior parte dei calcolatori algebrici. Si veda scomposizione dei polinomi. Sfortunatamente questi algoritmi sono troppo complicati da utilizzare sulla carta. A parte il calcolo euristico sopra accennato, solo pochi metodi si prestano a un calcolo manuale, e sono per polinomi di grado minore, con pochi coefficienti maggiori di zero. I principali di questi metodi sono descritti qui di seguito.
Fattorizzazione in parte primitiva e contenuto[modifica | modifica wikitesto]
Ogni polinomio a coefficienti razionali può essere fattorizzato in un unico modo come prodotto di un numero razionale e un polinomio a coefficienti interi primitivo (cioè l'MCD dei coefficienti è 1) e ha un coefficiente positivo iniziale (coefficiente del termine con il grado più elevato). Ad esempio:
In questa fattorizzazione, il numero razionale è detto contenuto e il polinomio primitivo è detto parte primitiva. Il calcolo di questa fattorizzazione può essere fatto come segue:
- Ridurre i coeficienti a un comune denominatore, per ottenere il quoziente intero di un polinomio a coefficienti interi.
- Raccogliere a fattore comune l'MCD dei coefficienti di questo polinomio per ottenere la parte primitiva, essendo il contenuto .
- Se necessario, cambiare di segno e tutti i coefficienti della parte primitiva.
Questa fattorizzazione può portare a un'espressione più estesa di quella originale (tipicamente quando ci sono molti denominatori interi coprimi), ma ciò nonostante la parte primitiva è generalmente più facile da manipolare per ulteriori fattorizzazioni.
Utilizzo del teorema del fattore[modifica | modifica wikitesto]
Il teorema del fattore afferma che se è una radice di un polinomio
con , allora esiste una fattorizzazione
dove
con . Il risultato della divisione lunga di un polinomio o quella sintetica è allora:
Tutto questo può essere utile quando si conosce o si intuisce qual è la radice del polinomio.
Ad esempio, per si può facilmente vedere che la somma dei coefficienti è 0, per cui è la radice. Siccome e , si ha
Radici razionali[modifica | modifica wikitesto]
Nel caso dei polinomi con coefficienti razionali, è possibile cercare le sue radici razionali. La fattorizzazione in parte primitiva e contenuto riduce il problema della ricerca di radici razionali al caso di polinomi a coefficienti interi aventi un massimo comundivisore uguale a 1.
Se è una radice razionale del polinomio
il teorema del fattore mostra che si ha la fattorizzazione
dove entrambi i fattori hanno coefficienti interi. Il fatto che abbia coefficienti interi deriva dalla formula sopraccitata del quoziente di diviso per .
Confrontando i coefficienti di grado con i coefficienti costanti dell'uguaglianza sopra, si nota che se è una radice razionale, in forma ridotta, allora è un divisore di e è un divisore di (teorema delle radici razionali). Di conseguenza, ci sono solo un numero finito di possibilità per e , che possono essere esaminate sistematicamente.[9]
Ad esempio, se il polinomio
ha radici razionali con , allora deve dividere 6, cioè e deve dividere 2, quindi . Inoltre, se , i termini del polinomio sono negativi, perciò una radice non può essere negativa. Si deve quindi avere
Un calcolo diretto mostra che solo è una radice, quindi non possono esserci altre radici razionali. Applicando il teorema del fattore si arriva alla fattorizzazione finale
Metodo quadratico AC[modifica | modifica wikitesto]
Questo metodo può essere adatto ai polinomi quadratici detto metodo AC di fattorizzazione.[10]
Si consideri il polinomio quadratico
con coefficienti interi. Se ha una radice razionale, il suo denominatore deve essere un divisore di e può essere scritto come una frazione riducibile . Tramite le formule di Viète, l'altra radice è
con . Quindi anche la seconda radice è razionale, e la seconda formula di Viète porta a
cioè
Controllando tutte le coppie di interi il cui prodotto è si ottengono, se esistono, le radici razionali.
Ad esempio, consideriamo il polinomio quadratico
Analizzando i possibili fattori di si trova che , che danno le radici
e la fattorizzazione
Utilizzo di formule per le radici dei polinomi[modifica | modifica wikitesto]
Qualsiasi polinomio quadratico a un'incognita può essere fattorizzato con la formula quadratica:
dove e sono le due radici del polinomio.
Se sono variabili reali, i fattori sono anch'essi reali se e solo se il discriminante è positivo. Altrimenti, il polinomio non può essere fattorizzato in fattori reali variabili.
La formula è valida quando i coefficienti appartengono a una caratteristica del campo numerico diversa da due, e in particolare, per coefficienti di un campo finito con un numero dispari di elementi.[N 1]
Ci sono pure formule per le radici dei polinomi cubici e quartici che sono, in generale, troppo complicate per un uso pratico. Il teorema di Abel-Ruffini afferma che non possono esserci formule generali per le radici di polinomi di grado cinque o superiore.
Utilizzo delle relazioni tra radici[modifica | modifica wikitesto]
Può capitare che si conosca qualche relazione tra le radici di un polinomio e i suoi coefficienti. L'uso di questa conoscenza può aiutare il lavoro di fattorizzazione del polinomio e la ricerca delle sue radici. La teoria di Galois è basata su uno studio sistematico di queste relazioni che includono le formule di Viète.
Qui ci limitiamo a considerare il caso più semplice di due radici e di un polinomio che soddisfa la relazione
dove è un polinomio.
Questo implica che è una radice comune a e , è quindi una radice del polinomio MCD di questi due polinomi. Da ciò segue che questo MCD è un fattore variabile di La divisione dei polinomi consente il calcolo dell'MCD.
Ad esempio,[11] se si conosce o si intuisce che: ha due radici la cui somma è zero, si può applicare l'algoritmo euclideo a e . Il primo passo della divisione consiste nell'aggiungere a ottenendo il resto di
Poi, dividendo per ottenendo zero come nuovo resto, e come quoziente, arrivando così alla completa fattorizzazione
Domini a fattorizzazione unica[modifica | modifica wikitesto]
Gli interi e i polinomi di un campo condividono la proprietà della fattorizzazione unica, cioè, ogni elemento diverso da zero può essere fattorizzato in un prodotto di un elemento invertibile (una unità, nel caso degli interi) e un prodotto di elementi irriducibili (numeri primi nel caso degli interi), e questa fattorizzazione è unica a meno dell'ordine degli elementi e dello spostamento delle unità tra i fattori. I domini di integrità che condividono questa proprietà sono detti domini a fattorizzazione unica (UFD).
L'MCD esiste negli UFD, e di converso, ogni dominio di integrità, nei quali esiste l'MCD, è un UFD. Ogni dominio ad ideali principali è un UFD.
Un dominio euclideo è un dominio di integrità nel quale è definita una divisione euclidea simile a quella degli interi. Ogni dominio euclideo è un dominio di ideali principale, e perciò un UFD.
In un dominio euclideo, la divisione euclidea consente la definizione di un algoritmo euclideo per il calcolo dell'MCD. Tuttavia, ciò non implica l'esistenza di un algoritmo di fattorizzazione. C'è un esempio esplicito di un campo in cui non può esistere qualsiasi algoritmo di fattorizzazione nel dominio euclideo dei polinomi a una incognita di .
Ideali[modifica | modifica wikitesto]
Nella teoria dei numeri algebrici, lo studio delle equazioni diofantee indusse i matematici, durante il XIX secolo, a introdurre una generalizzazione dei numeri interi detti interi algebrici. Il primo anello di interi algebrici preso in considerazione fu l'intero gaussiano e l'intero di Eisenstein, che condividono con gli interi usuali la proprietà di essere dominio ad ideali principali, aventi perciò la proprietà della fattorizzazione unica.
Sfortunatamente, la maggior parte degli algebrici interi si rivelarono subito come non principali e senza una fattorizzazione unica. Il più semplice di essi è nel quale
e tutti questi generi di fattori sono irriducibili.
Questa mancanza di un'unica fattorizzazione è una delle maggiori difficoltà per la soluzione delle equazioni diofantee. Per esempio, molte dimostrazioni errate dell'ultimo teorema di Fermat (probabilmente quelle dello stesso Pierre de Fermat) erano basate sull'implicita ipotesi della fattorizzazione unica.
Questa difficoltà fu risolta da Dedekind, che dimostrò che gli anelli degli interi algebrici hanno un'unica fattorizzazione in ideali: in questi anelli ogni ideale è il prodotto di primi ideali, e questa fattorizzazione è unica. I domini di integrità che possiedono questa proprietà di fattorizzazione unica sono ora detti domini di Dedekind. Essi hanno molte proprietà interessanti che li rendono fondamentali nella teoria dei numeri algebrici.
Matrici[modifica | modifica wikitesto]
Gli anelli di matrici sono non commutativi e non hanno un'unica fattorizzazione: ci sono, in generale, molti modi di scrivere una matrice come prodotto di matrici. Per cui il problema della fattorizzazione consiste nel trovare fattori di un tipo specifico. Per esempio, la decomposizione LU porta a una matrice risultante dal prodotto di una matrice triangolare inferiore (L) per una matrice triangolare superiore (U). Siccome ciò non è sempre possibile, in generale, si prova la decomposizione LUP avente una matrice di permutazione come terzo fattore.
Si veda la decomposizione di una matrice per i tipi più comuni di fattorizzazione di matrici.
Una matrice logica rappresenta una relazione binaria, e la moltiplicazione di matrici corrisponde a una composizione di relazioni. Scomporre una relazione tramite fattorizzazione serve a dare un profilo alla natura della relazione, come per esempio una relazione difunzionale.
Note[modifica | modifica wikitesto]
- Annotazioni
- ^ In un campo con caratteristica 2, si ha 2 = 0, e la formula porta ad una divisione per zero.
- Fonti
- ^ A. Facchini, Algebra e matematica discreta, Decibel Zanichelli, 2000, p. 28, ISBN 88-08-09739-0.
- ^ (EN) H. Hardy, An Introduction to the Theory of Numbers, Oxford Science Publications, 1980, ISBN 978-0198531715.
- ^ Klein, 1925
- ^ L’algebra nella matematica islamica – NUOVA STORIA VISUALE – NEW VISUAL HISTORY matematica-islamica/
- ^ In (EN) V. Sanford, A Short History of Mathematics, Read Books, 2008, ISBN 9781409727101., l'autore nota "Vista la presente enfasi data alla soluzione delle equazioni quadratiche mediante fattorizzazione, è interessante notare che questo metodo non era in uso prima del lavoro del 1631 di Harriot".
- ^ frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false Harriot, Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas
- ^ Fite, 1921
- ^ Selby, 1970
- ^ Dickson, 1922
- ^ Stover, Christopher AC Method - Mathworld Archiviato il 28 aprile 2021 in Internet Archive.
- ^ Burnside Panton, 1960
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «fattorizzazione»
Wikizionario contiene il lemma di dizionario «fattorizzazione»
Collegamenti esterni[modifica | modifica wikitesto]
- fattorizzazione, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- fattorizzazione, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Eric W. Weisstein, Fattorizzazione, su MathWorld, Wolfram Research.
- (EN) Fattorizzazione, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
| Controllo di autorità | Thesaurus BNCF 30495 · LCCN (EN) sh85046844 · BNF (FR) cb122865337 (data) · J9U (EN, HE) 987007565462605171 |
|---|





























































































































































































![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216)
![{\displaystyle \mathbb {Z} [{\sqrt {-5}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1)
