Pentagono
In geometria, un pentagono è un poligono di cinque lati e cinque angoli, congruenti o meno, regolare o irregolare, che può essere concavo o convesso, semplice o complesso (intrecciato). Un caso particolare di pentagono intrecciato è il pentagramma, la cui forma più nota può essere ottenuta da un pentagono regolare estendendone i lati, oppure disegnandone le diagonali: è la cosiddetta stella a cinque punte che si può ripetere un'infinità di volte dentro un pentagono.
La somma degli angoli interni è di 540°.
Etimologia[modifica | modifica wikitesto]
Il suo nome deriva direttamente dal termine del greco antico "πεντάγωνον",[1] pentàgonon, avente l'identico significato, "pentagono" (usato da Aristotele e da Ateneo Meccanico),[2] termine a sua volta derivante da "πέντε", pente, ossia “cinque”[3] (che diviene “πέντα” in parole composte), e “-γωνον”, -gonon, al posto di “γωνία”, gonía, cioè “angolo”;[2] ciò sta ad indicare una figura geometrica con cinque angoli e, di conseguenza, cinque lati.
Pentagono regolare[modifica | modifica wikitesto]

Per definizione, un pentagono regolare: è
- un poligono convesso costituito da cinque angoli e da cinque lati;
- i cinque lati sono congruenti;
- i cinque angoli sono anch'essi congruenti (in Fig. 1 uno degli angoli interni è identificato con la lettera γ).
Da queste definizioni si può dedurre che tutte le diagonali del pentagono sono congruenti, in quanto lati omologhi dei triangoli ABC, BCD, CDE, DEA e EAB, che sono a loro volta congruenti: hanno infatti due lati che coincidono con i lati del pentagono, i quali definiscono gli angoli interni del pentagono stesso (lati e angoli interni del pentagono regolare che, come detto, sono congruenti per definizione).
Circonferenze circoscritta ed inscritta[modifica | modifica wikitesto]
La definizione di pentagono regolare non implica automaticamente che tale poligono sia circoscrivibile o inscrivibile in una circonferenza, ma tale fatto può essere facilmente dimostrato. Bisecando ogni angolo interno del pentagono si ottiene la serie di triangoli AOB, BOC, COD... che sono tutti isosceli, in quanto gli angoli che giacciono sulle loro basi AB, BC, CD... sono ciascuno metà degli angoli interni del pentagono. I segmenti AO e BO sono quindi congruenti; ma lo sono anche BO e CO, CO e DO... di conseguenza:
- i vertici del pentagono sono equidistanti dal punto O, che è quindi il centro della circonferenza circoscritta al pentagono stesso;
- i triangoli che hanno come base i lati del pentagono e come vertice il punto O sono congruenti;
- gli angoli al centro del pentagono, ovvero gli angoli che dal centro della circonferenza circoscritta sottendono ciascun lato del pentagono stesso, sono congruenti;
- le altezze tracciate a partire dal punto O sui lati del pentagono (es. segmento OF in Fig. 1) sono congruenti;
- nel pentagono regolare può essere inscritta una circonferenza (arco tratteggiato in Fig. 1), tangente ai lati del pentagono nei punti di base delle altezze tracciate da O, e il cui raggio coincide con la lunghezza di tali altezze. Il raggio della circonferenza inscritta è detto apotema.
Angoli[modifica | modifica wikitesto]
Stabilito il fatto che un pentagono regolare può essere inscritto in una circonferenza, si può quantificare l'ampiezza degli angoli al centro, ovvero degli angoli che dal centro O della circonferenza sottendono ciascuno dei lati del pentagono:
Il punto E giace sulla circonferenza circoscritta al pentagono, quindi gli angoli AEB, BEC e CED, che sottendono rispettivamente gli archi (e le relative corde / lati) AB, BC e CD, hanno ampiezza ciascuno metà dell'angolo al centro:
Di conseguenza l'angolo interno del pentagono vale:
Esaminiamo ora la relazione fra lati e diagonali. Ogni diagonale del pentagono è parallela al lato opposto (ovvero a quello fra i lati del pentagono che non tocca una delle estremità della diagonale presa in esame). Verificando un caso particolare, si può vedere che gli angoli BEC e ECD sono alterni interni delle rette BE e CD tagliate dalla trasversale CE; essendo tali angoli congruenti (entrambi di ampiezza pari a β), il lato CD e la diagonale BE risultano appunto essere paralleli. Lo stesso vale per ogni altra coppia lato / diagonale del pentagono.
Ulteriore caratteristica dell'angolo β è di comparire un totale di 5 volte in ciascuno dei triangoli costituiti da due diagonali e un lato del pentagono (es. il triangolo BDE). Tali triangoli sono ovviamente isosceli, in quanto è già stato dimostrato che le diagonali del pentagono sono congruenti; in più, l'angolo in B, compreso fra le due diagonali, è metà di ciascuno degli altri due angoli: questo tipo di triangolo, in cui due angoli sono ciascuno il doppio del terzo, viene chiamato Triangolo Aureo, ed è fondamentale per procedere alla costruzione del pentagono regolare secondo il metodo descritto da Euclide.
Lunghezze del lato e della diagonale[modifica | modifica wikitesto]

Osservazione preliminare: il triangolo ABG è isoscele in quanto gli angoli in A e in B sono congruenti: ne consegue che sono congruenti tutti i segmenti come BG e CJ (che serviranno fra poco) che partono dai vertici del pentagono ABCDE per congiungersi ai vertici del pentagono interno GHJKL, costruito dalle diagonali.
Si osservi ora che i triangoli BAE e CJD sono simili, in quanto i lati omologhi sono tutti paralleli fra loro. Vale dunque la proporzione:
Osserviamo ora la diagonale BE, tagliata in G dalla diagonale AC. Il segmento GE ha ovviamente la stessa lunghezza sia di CD (CDEG è un parallelogramma) che di BA, mentre abbiamo già dimostrato che BG e CJ sono congruenti. Quindi possiamo riscrivere la precedente proporzione con i segmenti seguenti:
La proporzione qui sopra ha la forma classica , quella che definisce la sezione aurea. Ne consegue che la lunghezza s del lato del pentagono rispetto alla sua diagonale d è:
Viceversa:
Nel triangolo BDE si tracci l'altezza dal vertice B al piede S, e si prolunghi il segmento fino ad incontrare la circonferenza circoscritta al pentagono in T. Per costruzione, l'angolo BSE è retto, quindi si può applicare il teorema di Pitagora per calcolare la lunghezza del segmento BS:
Infine si può calcolare la lunghezza del segmento BT, che è un diametro della circonferenza circoscritta, e quindi vale due volte il raggio r della medesima: considerando il fatto che i triangoli BSE e BTE sono simili (sono entrambi rettangoli, e hanno il vertice B in comune), si imposta la proporzione:
da cui
Invertendo quest'ultima espressione possiamo ricavare la lunghezza della diagonale rispetto al raggio:
Il rapporto già calcolato fra lunghezze del diametro e del lato ci consente di ricavare la lunghezza del lato rispetto al raggio:
Infine, per completezza, si può calcolare la lunghezza del segmento ET, che è il lato del decagono inscritto nella stessa circonferenza del pentagono (questo dato sarà utile per descrivere la costruzione del pentagono regolare secondo Tolomeo). Come già detto, il triangolo BTE è rettangolo, quindi si può di nuovo applicare il teorema di Pitagora:
Incommensurabilità di lato e diagonale[modifica | modifica wikitesto]

Come già mostrato, il lato e la diagonale del pentagono regolare stanno fra loro come il rapporto aureo. Quella che segue è la dimostrazione che tale rapporto è incommensurabile, ovvero che il rapporto fra dette lunghezze non può essere espresso da un numero razionale.
La dimostrazione che segue prende le mosse dalla Proposizione 2 del libro X degli Elementi di Euclide: Se di due grandezze disuguali veniamo a sottrarre [...] la minore dalla maggiore quante volte sia possibile, e quella restante non misura mai la grandezza ad essa precedente, le grandezze sono incummensurabili.
Prendiamo quindi in esame (vedi Fig. 3) il pentagono ABCDE, la sua diagonale BE e il lato BA, minore di BE. Occorre ricavare la differenza fra queste due lunghezze: si traccia quindi l'arco AH, centrato in B e di raggio BA, fino a intersecare BE nel punto H; e dato che BH e BA sono congruenti, il segmento HE è la differenza cercata.
H divide il segmento BE in "media ed estrema ragione": ciò significa che BH e HE stanno anch'essi fra loro come diagonale e lato di un pentagono regolare, che può essere facilmente costruito. Tracciando l'arco EAJ, centrato in H e con raggio HE, si trova il punto J sul segmento BA. A questo punto BH è la diagonale del pentagono BFGHJ, in cui i lati BJ e JH sono congruenti con HE (non occorre in questa sede descrivere in che modo si determinano i punti F e G).
Ricapitoliamo: dati i segmenti BE (diagonale) e BA = BH (lato del pentagono) si trova la loro differenza HE = BJ; ma BH e BJ sono rispettivamente diagonale e lato del nuovo pentagono BFGHJ. Per proseguire secondo quanto disposto dalla citata proposizione di Euclide, occorre adesso trovare la differenza fra BH e BJ: ripetendo il meccanismo descritto sopra si trova il punto M, che fa parte del pentagono BKLMN. Ripetendo ancora il procedimento si ottiene il pentagono BOPQR, e così via: per quante volte si ripeta la costruzione, si troveranno sempre coppie di segmenti che stanno fra loro come il rapporto aureo; non arrivando mai ad ottenere due segmenti misurabili (secondo la proposizione di Euclide) ne risulterà che lato e diagonale del pentagono regolare sono incommensurabili.
Apotema[modifica | modifica wikitesto]
L'apotema può essere calcolato sottraendo la lunghezza di un raggio dal segmento h (si vedano per chiarezza in Fig. 2 i segmenti BT e AF, congruenti):
Un ultimo valore, che serve per calcolare l'area del pentagono regolare, è il cosiddetto Numero Fisso, definito come rapporto fra apotema e lato:
Determinazione delle lunghezze per via trigonometrica[modifica | modifica wikitesto]

L'uso della trigonometria consente la determinazione delle lunghezze significative del pentagono regolare in modo più semplice rispetto a quello descritto sopra, anche se presenta alcune controindicazioni:
- l'uso di tabelle o calcolatori elettronici consente solo la determinazione approssimata delle lunghezze, non le espressioni algebriche basate su radicali che determinano tali lunghezze in modo esatto;
- non tutti coloro che si interessano di geometria classica conoscono la trigonometria;
- da un punto di vista storico, la trigonometria si sviluppa con Tolomeo, almeno quattro secoli dopo Euclide, che a sua volta segue di secoli gli studi pionieristici della scuola Pitagorica.
Dalla Fig. 4 si può ricavare il modo più semplice per determinare le varie lunghezze in base al raggio della circonferenza circoscritta. Dati l'angolo α che coincide con l'angolo al centro del pentagono; e β, metà di tale valore, si ricava facilmente che il lato del pentagono CD vale:
L'apotema OF:
La diagonale BE:
Area[modifica | modifica wikitesto]
L'area del pentagono è la somma delle aree di 5 triangoli con base pari al lato e altezza pari all'apotema. Di seguito le formule per il calcolo dell'area in base alle lunghezze del lato e del raggio della circonferenza circoscritta:
Rapporti fra lunghezze[modifica | modifica wikitesto]
Nella tabella che segue si danno i valori esatti ed approssimati delle lunghezze del raggio r della circonferenza circoscritta, del lato s, della diagonale d, dell'apotema a, e dell'area A, in base a ciascuno degli stessi elementi lineari:
| Raggio (r) | Lato (s) | Diagonale (d) | Apotema (a) | Area (A) |
|---|---|---|---|---|
Costruzione del pentagono regolare[modifica | modifica wikitesto]

Nel corso della storia sono stati proposti vari modi per disegnare un Pentagono Regolare con riga e compasso. Di seguito ne vengono mostrati alcuni esempi notevoli.
Costruzione secondo Euclide[modifica | modifica wikitesto]
Nei suoi Elementi, Euclide prende in considerazione il triangolo aureo costituito da due diagonali e un lato del pentagono regolare, del quale sfrutta le seguenti caratteristiche:
- Gli angoli interni di due angoli sono il doppio dell'angolo rimanente;
- Il rapporto fra ciascuno dei due lati e la base è pari alla sezione aurea.
In Fig. 5 è mostrata una sintesi delle proposizioni descritte da Euclide, con la sola differenza per cui, per semplicità, invece di inscrivere il pentagono in una circonferenza data, se ne costruisce uno a partire da una sua diagonale:
- le linee verdi indicano la divisione del segmento BE in "media ed estrema ragione", ovvero la determinazione del punto K che lo divide in modo che la maggiore delle sue parti sia media proporzionale tra la minore e la somma delle due[4]: sul lato BE si costruisce il quadrato BFGE; si traccia il punto H intermedio al segmento FB, e si prolunga il segmento FB oltre B. Si determina il punto J con un arco centrato in H e raggio HE, poi con l'arco JAK centrato in B e raggio BJ si determina il punto K, che è quello cercato;
- le linee rosse indicano la costruzione del Triangolo Aureo[5]: il punto C è l'intersezione fra gli archi centrati in B ed E, di raggio rispettivamente pari a BK (lato del pentagono) ed EB (diagonale dello stesso);
- a differenza di Euclide, che inscrive il triangolo ottenuto in un cerchio dato[6], qui come accennato si vuole tracciare un Pentagono regolare partendo da una sua diagonale. Si traccia quindi il cerchio circoscritto al triangolo BCE[7]: si tratta della circonferenza ABCDE di cui qui si omettono i passaggi necessari a determinarne il centro;
- i punti B, C e D sono punti già noti del pentagono cercato; il punto A è l'intersezione fra l'arco JAK e la circonferenza ABCDE; il punto D viene trovato con un arco centrato in E e di raggio AE.
Costruzione secondo Tolomeo[modifica | modifica wikitesto]


La costruzione più nota del Pentagono Regolare non è quella proposta da Euclide, ma deriva da un abbozzo che compare nell'Almagesto di Tolomeo[8]. In effetti Tolomeo non si propone di costruire un pentagono regolare, bensì di determinare la lunghezza della corda sottesa da un angolo al centro di 72°, proprio la lunghezza del lato del pentagono (da questo valore ricaverà lo scheletro della sua Tavola delle Corde, comprendente la lunghezza delle corde di tutti gli angoli multipli di 12°).
Vediamo quindi i passaggi proposti da Tolomeo, integrati da quelli che servono all'effettiva costruzione del pentagono regolare (vedi Fig. 6):
- Sia data una circonferenza centrata in O, della quale due assi ortogonali siano OA e OP; si trovi il punto L intermedio fra O e P. Mediante il Teorema di Pitagora, si calcola la lunghezza del segmento AL rispetto al raggio della circonferenza:
- Si tracci l'arco AM centrato in L di raggio AL. La lunghezza del segmento OM, che coincide con la lunghezza del lato del decagono regolare inscritto nella circonferenza, è:
- Tracciando l'arco BME con centro in A e raggio AM si determinano i punti B ed E che, assieme ad A, costituiscono i primi tre punti del pentagono. Infatti il segmento AM ha proprio la lunghezza del lato del pentagono (si tenga presente che il segmento OA è un raggio della circonferenza circoscritta):
- La determinazione dei rimanenti punti C e D può essere fatta riportando la lunghezza del lato AB più volte sulla circonferenza, ma c'è un modo molto più elegante. Prolungando l'arco AM, centrato in L, fino al punto N di intersezione con l'asse orizzontale, si determina il segmento AN la cui lunghezza coincide con la diagonale del pentagono, quindi è sufficiente tracciare l'arco NDC, centrato in A, per trovare i due punti mancanti. Infatti:
Il fatto che i lati del decagono, esagono e pentagono regolari inscritti in circonferenze di pari raggio costituiscono i lati di un triangolo rettangolo era già stato dimostrato da Euclide[9]. Egli usa però questa dimostrazione non per la costruzione del pentagono regolare, ma dell'Icosaedro inscritto in una sfera[10].
Costruzione con un cerchio di Carlyle[modifica | modifica wikitesto]

È noto che i vertici di un pentagono regolare, inscritto in un cerchio di raggio unitario, possono essere determinati risolvendo l'equazione ciclotomica
le cui radici sono date dall'espressione
per n compreso fra 0 e 4. Dato che l'equazione ciclotomica non ha termini di grado 1, sommando tutte le soluzioni si ottiene 0. Pertanto, se dal totale togliamo ξ0=1, la somma delle rimanenti radici è -1. Inoltre, dalla formula di Eulero segue che:
da cui si possono ricavare le seguenti relazioni:
Queste espressioni danno luogo a un'equazione di secondo grado, che può facilmente essere risolta tramite un cerchio di Carlyle:
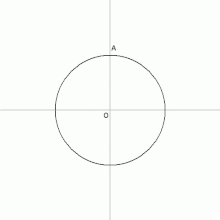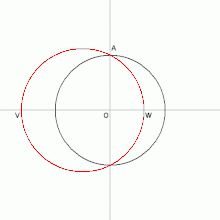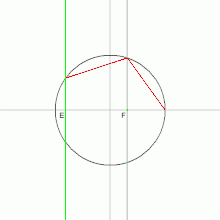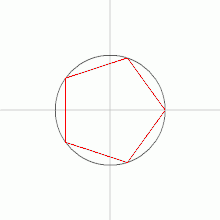
- Si trovano i punti A e B di coordinate (0,1) e (s, p).
- Si costruisce la circonferenza il cui diametro è il segmento AB. Il centro M di tale circonferenza risulterà avere coordinate (-1/2,0).
Le intersezioni della circonferenza con l'asse delle ascisse sono i punti V e W. La bisezione dei segmenti OV e OW determina i punti E ed F, che sono le ascisse dei vertici del pentagono.
Altra costruzione a partire dal lato[modifica | modifica wikitesto]
Il primo obiettivo è trovare il vertice opposto al lato grazie alla formula dove d è la diagonale ed l è il lato.
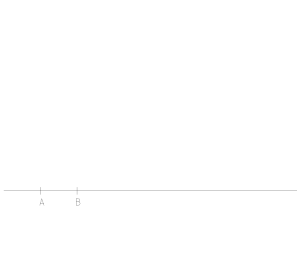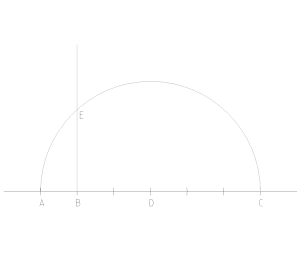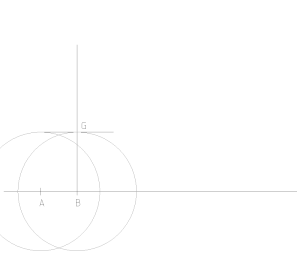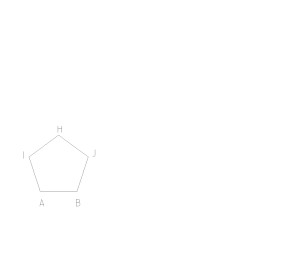
Con riferimento a fig. 10, si parta dal lato AB.
- Si estenda per 5 volte il lato AB sul suo prolungamento, fino ad avere un segmento AC = 6AB;
- si tracci un semicerchio di centro D (punto mediano di AC) e diametro AC;
- si tracci la perpendicolare di AC passante per B. Per il secondo teorema di Euclide, BE è medio proporzionale tra AB e BC, cioè tra l e 5l. Quindi ;
- si estenda il segmento BE per un'ulteriore lunghezza AB, trovando ;
- si divida per due BF, ricavando la lunghezza BG in rapporto aureo con il lato l;
- si traccino due cerchi di raggio BG, uno centrato in B e uno in A;
- la loro intersezione è il vertice H opposto ad AB.
Il secondo obiettivo è trovare gli altri due vertici del pentagono regolare.
- Si traccino tre cerchi di raggio AB; uno centrato in A, uno centrato in B ed uno centrato in H;
- le intersezioni tra il cerchio centrato in A e quello centrato in H sono equidistanti dai due vertici. Si scelga quella più a sinistra per il punto I;
- le intersezioni tra il cerchio centrato in B e quello centrato in H sono equidistanti dai due vertici. Si scelga quella più a destra per il punto J.
Si uniscano i vertici AB, BJ, JH, HI ed IA, ottenendo il pentagono regolare ABJHI.
Note[modifica | modifica wikitesto]
- ^ pentagono - Treccani, su Treccani. URL consultato il 15 aprile 2024.
- ^ a b Lorenzo Rocci, Vocabolario Greco Italiano, 37ª ed., Società editrice Dante Alighieri, 1993, p. 1458.
- ^ Lorenzo Rocci, Vocabolario Greco Italiano, 37ª ed., Società editrice Dante Alighieri, 1993, p. 1459.
- ^ Euclide, Elementi, Libro II, proposizione 11: Dividere un segmento dato in modo che il rettangolo compreso da tutta la retta e da una delle parti sia uguale al quadrato della parte rimanente.
- ^ Euclide, Elementi, Libro IV, proposizione 11: Costruire un triangolo isoscele avente ciascuno dei due angoli alla base che sia il doppio dell'angolo rimanente.
- ^ Euclide, Elementi, Libro IV, proposizione 11: Iscrivere in un cerchio dato un pentagono equilatero ed equiangolo
- ^ Euclide, Elementi, Libro IV, Proposizione 5: Circoscrivere un cerchio ad un triangolo dato.
- ^ Tolomeo, Almagesto, Libro I - 10: sulla misura delle corde
- ^ Euclide, Elementi, Libro XIII, Proposizione 10: Se si iscrive in un cerchio un pentagono equilatero, il quadrato del lato del pentagono è uguale alla somma dei quadrati dei lati dell'esagono e del decagono regolari che siano inscritti nello stesso cerchio.
- ^ Euclide, Elementi, Libro XIII, Proposizione 16: Costruire un icosaedro iscrivendolo in una sfera di diametro dato
Voci correlate[modifica | modifica wikitesto]
- Costruzioni con riga e compasso
- Poligono regolare
- Cerchio di Carlyle
- Eptadecagono
- 257-gono
- 65537-gono
- Dodecaedro
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «pentagono»
Wikizionario contiene il lemma di dizionario «pentagono» Wikimedia Commons contiene immagini o altri file sul pentagono
Wikimedia Commons contiene immagini o altri file sul pentagono
Collegamenti esterni[modifica | modifica wikitesto]
- Pentagono, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- Pentagono, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- Pentàgono, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
- pentàgono, su sapere.it, De Agostini.
- Pentagono, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Opere riguardanti Pentagon, su Open Library, Internet Archive.
- (EN) Eric W. Weisstein, Pentagon, su MathWorld, Wolfram Research.
| Controllo di autorità | Thesaurus BNCF 6800 |
|---|







































































