Distribuzione chi quadrato

Distribuzione $\chi^2(k)$
Funzione di densità di probabilità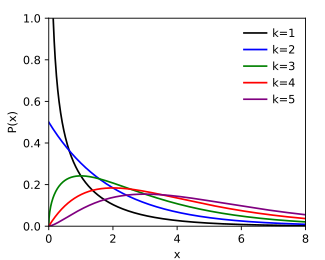
Funzione di ripartizione
Parametri	$k\in\mathbb{N}\setminus\{0\}$ (gradi di libertà)
Supporto	$x\in[0,\infty]$
Funzione di densità	$\frac{1}{2^{k/2}\Gamma(k/2)} x^{k/2-1} e^{-x/2}$
Funzione di ripartizione	$\frac{1}{\Gamma(k/2)}\gamma(k/2,x/2)$
Valore atteso	$k$
Mediana	circa $k\bigg(1-\frac{2}{9k}\bigg)^3$
Moda	$\max\{k-2,0\}$
Varianza	$2k$
Skewness	$\sqrt{8/k}$
Curtosi	$12/k$
Entropia	$\frac{k}{2}+\ln(2\Gamma(k/2))+(1-k/2)\psi(k/2)$
Funz. Gen. dei Momenti	$(1-2t)^{-k/2}$ per $-1/2\geqslant t\geqslant 1/2$
Funz. Caratteristica	$(1-2\,i\,t)^{-k/2}$

In teoria delle probabilità una distribuzione $\chi^2$ (chi quadrato o chi-quadro^[1]) è una distribuzione di probabilità che descrive la somma dei quadrati di alcune variabili aleatorie indipendenti aventi distribuzione normale standard.

In statistica viene particolarmente utilizzata per l'omonimo test di verifica d'ipotesi (test χ²).

[modifica] Definizione

La distribuzione $\chi^2(k)$ descrive la variabile aleatoria

$x^2=\sum_{i=1}^k x_i^2=x_1^2+\ldots+x_k^2$ ,

dove $x_1,...,x_k$ sono variabili aleatorie indipendenti con distribuzione normale standard $\mathcal{N}(0,1)$ . Il parametro k è detto numero di gradi di libertà.

[modifica] Storia

Ernst Abbe (1840-1905), un ottico, fu colui che scoprì la χ² analizzando la sommatoria di variabili casuali normali standardizzate e indipendenti, che produce una nuova variabile casuale, la χ² appunto.^[2]

[modifica] Proprietà

[modifica] Somma

Per definizione, la somma di due variabili aleatorie indipendenti con distribuzioni χ²(m) e χ²(n) è una variabile aleatoria con distribuzione χ²(m+n):

$(x_1^2+...+x_m^2)+(x_{m+1}^2+...+x_{m+n}^2)=x_1^2+...+x_{m+n}^2$

Più in generale la somma di variabili aleatorie indipendenti con distribuzioni χ²(k₁), ..., χ²(k_n), è una variabile aleatoria con distribuzione χ²(k₁+...+k_n).

[modifica] Caratteristiche

Una generalizzazione della distribuzione χ² è la distribuzione Gamma: $\textstyle\Gamma(\frac{k}{2},\frac{1}{2})=\chi^2(k)$ .

In particolare una variabile aleatoria $x^2$ con distribuzione $\chi^2(k)$ ha

funzione di densità di probabilità $f_k(x)=\frac{1}{2^{k/2}\Gamma(k/2)} x^{k/2-1} e^{-x/2}$ per x>0,

dove Γ indica la funzione Gamma, che qui assume i valori $\textstyle(\frac{1}{2}n) = \sqrt{\pi} \frac{(n-2)!!}{2^{(n-1)/2}}$ ,

con !! che indica il doppio fattoriale;

funzione di ripartizione $F_k(x)=\frac{1}{\Gamma(k/2)}\gamma(k/2,x/2)$ ,

dove γ è la funzione $\textstyle \gamma(s,x) = \int_0^x t^{s-1} e^{-t} dt$

valore atteso $\mathbb E[x]=k$ ;
varianza $\sigma^2(x^2)=2k$ ;
simmetria: $\gamma_1=\sqrt{8/k}$
curtosi: $\gamma_2=12/k$
moda: $\max\{0,k-2\}$

[modifica] Limite centrale

Per il teorema del limite centrale la distribuzione χ²(k) converge ad una distribuzione normale per k che tende a infinito. Più precisamente, se $y_k^2=x_1^2+...+x_k^2$ segue la distribuzione χ², allora la distribuzione di

$\frac{y_k^2-k}{\sqrt{2k}}$

tende alla distribuzione normale standard $\mathcal{N}(0,1)$ .

Per avere una convergenza più rapida talvolta vengono prese $\sqrt{2y_k^2}$ o $\sqrt[3]{y_k^2/k}$ .

[modifica] Generalizzazioni

La distribuzione χ² è un caso particolare della legge Γ e ricade nella terza famiglia di distribuzioni di Pearson.

La distribuzione χ² non centrale è data dalla somma dei quadrati di variabili aleatorie indipendenti $x_1,...,x_k$ aventi distribuzioni normali ridotte, ma non necessariamente centrate, $\mathcal{N}(\mu_1,1),...,\mathcal{N}(\mu_k,1)$ :

$x^2=x_1^2+\ldots+x_k^2$

Un'altra generalizzazione prevede di considerare una forma quadratica $V^tAV$ sul vettore aleatorio $v=(x_1,...,x_k)$ .

[modifica] Utilizzo in statistica

In statistica la distribuzione χ² viene utilizzata per condurre il test di verifica d'ipotesi χ² e per stimare una varianza, ed è legato alle distribuzioni distribuzione t di Student e distribuzione F di Fisher-Snedecor.

Il caso più comune è quello di variabili aleatorie indipendenti $x_1,...,x_n$ di legge normale $\mathcal{N}(\mu,\sigma)$ e media $\textstyle \bar{x}=\frac{1}{n}\sum_{i=1}^nx_i$ , dove lo stimatore della varianza

$S^2_{n-1} =\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1}$

segue la distribuzione

$\frac{\sigma^2}{n-1}\chi^2(n-1)$ .

Per valori di k superiori a 30 (o a 50) la legge χ² viene approssimata con una legge normale.

[modifica] Tabella dei valori critici

La seguente tabella illustra alcuni valori critici più comunemente utilizzati. In corrispondenza dei valori k sulla riga e α sulla colonna si trova il valore critico $z_\alpha=F_k^{-1}(\alpha)$ , ovvero il valore per il quale una variabile aleatoria x² di legge χ²(k) verifica

$P(x^2<z_\alpha)=\alpha\$ .

k \ α	0.001	0.002	0.005	0.01	0.02	0.05	0.1	0.2	0.5	0.75	0.8	0.9	0.95	0.98	0.99	0.995	0.998	0.999
1	0.000	0.000	0.000	0.000	0.001	0.004	0.016	0.064	0.455	1.323	1.642	2.706	3.841	5.412	6.635	7.879	9.550	10.828
2	0.002	0.004	0.010	0.020	0.040	0.103	0.211	0.446	1.386	2.773	3.219	4.605	5.991	7.824	9.210	10.597	12.429	13.816
3	0.024	0.039	0.072	0.115	0.185	0.352	0.584	1.005	2.366	4.108	4.642	6.251	7.815	9.837	11.345	12.838	14.796	16.266
4	0.091	0.129	0.207	0.297	0.429	0.711	1.064	1.649	3.357	5.385	5.989	7.779	9.488	11.668	13.277	14.860	16.924	18.467
5	0.210	0.280	0.412	0.554	0.752	1.145	1.610	2.343	4.351	6.626	7.289	9.236	11.070	13.388	15.086	16.750	18.907	20.515
6	0.381	0.486	0.676	0.872	1.134	1.635	2.204	3.070	5.348	7.841	8.558	10.645	12.592	15.033	16.812	18.548	20.791	22.458
7	0.598	0.741	0.989	1.239	1.564	2.167	2.833	3.822	6.346	9.037	9.803	12.017	14.067	16.622	18.475	20.278	22.601	24.322
8	0.857	1.038	1.344	1.646	2.032	2.733	3.490	4.594	7.344	10.219	11.030	13.362	15.507	18.168	20.090	21.955	24.352	26.124
9	1.152	1.370	1.735	2.088	2.532	3.325	4.168	5.380	8.343	11.389	12.242	14.684	16.919	19.679	21.666	23.589	26.056	27.877
10	1.479	1.734	2.156	2.558	3.059	3.940	4.865	6.179	9.342	12.549	13.442	15.987	18.307	21.161	23.209	25.188	27.722	29.588
11	1.834	2.126	2.603	3.053	3.609	4.575	5.578	6.989	10.341	13.701	14.631	17.275	19.675	22.618	24.725	26.757	29.354	31.264
12	2.214	2.543	3.074	3.571	4.178	5.226	6.304	7.807	11.340	14.845	15.812	18.549	21.026	24.054	26.217	28.300	30.957	32.909
13	2.617	2.982	3.565	4.107	4.765	5.892	7.042	8.634	12.340	15.984	16.985	19.812	22.362	25.472	27.688	29.819	32.535	34.528
14	3.041	3.440	4.075	4.660	5.368	6.571	7.790	9.467	13.339	17.117	18.151	21.064	23.685	26.873	29.141	31.319	34.091	36.123
15	3.483	3.916	4.601	5.229	5.985	7.261	8.547	10.307	14.339	18.245	19.311	22.307	24.996	28.259	30.578	32.801	35.628	37.697
16	3.942	4.408	5.142	5.812	6.614	7.962	9.312	11.152	15.338	19.369	20.465	23.542	26.296	29.633	32.000	34.267	37.146	39.252
17	4.416	4.915	5.697	6.408	7.255	8.672	10.085	12.002	16.338	20.489	21.615	24.769	27.587	30.995	33.409	35.718	38.648	40.790
18	4.905	5.436	6.265	7.015	7.906	9.390	10.865	12.857	17.338	21.605	22.760	25.989	28.869	32.346	34.805	37.156	40.136	42.312
19	5.407	5.969	6.844	7.633	8.567	10.117	11.651	13.716	18.338	22.718	23.900	27.204	30.144	33.687	36.191	38.582	41.610	43.820
20	5.921	6.514	7.434	8.260	9.237	10.851	12.443	14.578	19.337	23.828	25.038	28.412	31.410	35.020	37.566	39.997	43.072	45.315
21	6.447	7.070	8.034	8.897	9.915	11.591	13.240	15.445	20.337	24.935	26.171	29.615	32.671	36.343	38.932	41.401	44.522	46.797
22	6.983	7.636	8.643	9.542	10.600	12.338	14.041	16.314	21.337	26.039	27.301	30.813	33.924	37.659	40.289	42.796	45.962	48.268
23	7.529	8.212	9.260	10.196	11.293	13.091	14.848	17.187	22.337	27.141	28.429	32.007	35.172	38.968	41.638	44.181	47.391	49.728
24	8.085	8.796	9.886	10.856	11.992	13.848	15.659	18.062	23.337	28.241	29.553	33.196	36.415	40.270	42.980	45.559	48.812	51.179
25	8.649	9.389	10.520	11.524	12.697	14.611	16.473	18.940	24.337	29.339	30.675	34.382	37.652	41.566	44.314	46.928	50.223	52.620
26	9.222	9.989	11.160	12.198	13.409	15.379	17.292	19.820	25.336	30.435	31.795	35.563	38.885	42.856	45.642	48.290	51.627	54.052
27	9.803	10.597	11.808	12.879	14.125	16.151	18.114	20.703	26.336	31.528	32.912	36.741	40.113	44.140	46.963	49.645	53.023	55.476
28	10.391	11.212	12.461	13.565	14.847	16.928	18.939	21.588	27.336	32.620	34.027	37.916	41.337	45.419	48.278	50.993	54.411	56.892
29	10.986	11.833	13.121	14.256	15.574	17.708	19.768	22.475	28.336	33.711	35.139	39.087	42.557	46.693	49.588	52.336	55.792	58.301
30	11.588	12.461	13.787	14.953	16.306	18.493	20.599	23.364	29.336	34.800	36.250	40.256	43.773	47.962	50.892	53.672	57.167	59.703
35	14.688	15.686	17.192	18.509	20.027	22.465	24.797	27.836	34.336	40.223	41.778	46.059	49.802	54.244	57.342	60.275	63.955	66.619
40	17.916	19.032	20.707	22.164	23.838	26.509	29.051	32.345	39.335	45.616	47.269	51.805	55.758	60.436	63.691	66.766	70.618	73.402
45	21.251	22.477	24.311	25.901	27.720	30.612	33.350	36.884	44.335	50.985	52.729	57.505	61.656	66.555	69.957	73.166	77.179	80.077
50	24.674	26.006	27.991	29.707	31.664	34.764	37.689	41.449	49.335	56.334	58.164	63.167	67.505	72.613	76.154	79.490	83.657	86.661

[modifica] Derivazione

[modifica] Derivazione della funzione di densità per un grado di libertà

Sia y = x², dove x è una variabile casuale normalmente distribuita con media nulla e varianza unitaria (x ~ N(0,1)).

Allora, se $y<0, ~ P(y<y)=0$ , mentre, se $y\geq0, ~ P(y<y) = P(x^2<y)=P(|x|<\sqrt{y})=F_x(\sqrt{y})-F_x(-\sqrt{y})$ .

$f_y(y) = f_x(\sqrt{y})\frac{\partial(\sqrt{y})}{\partial y}-f_x(-\sqrt{y})\frac{\partial(-\sqrt{y})}{\partial y}$

$= \frac{1}{\sqrt{2\pi}}\frac{1}{2y^{1/2}}e^{-\frac{y}{2}} + \frac{1}{\sqrt{2\pi}}\frac{1}{2y^{1/2}}e^{-\frac{y}{2}} = \frac{1}{\sqrt{2\pi}}\frac{1}{y^{1/2}}e^{- \frac{y}{2}}$

$= \frac{1}{2^{\frac{1}{2}} \Gamma(\frac{1}{2})}y^{\frac{1}{2} -1}e^{-\frac{y}{2}}$

dove $F$ e $f$ sono, rispettivamente, la funzione di densità e la funzione di probabilità cumulata.

Si ha quindi: $y = x^2 \sim \chi^2_1$ .

[modifica] Derivazione della funzione di densità per due gradi libertà

È possibile derivare la distribuzione con 2 gradi di libertà partendo da quella con un grado.

Siano x e y due variabili casuali indipendenti tali che $x \sim \chi^2_1$ e $y \sim \chi^2_1$ .

Dall'assunto di indipendenza segue che la loro funzione di probabilità congiunta è:

$f_{xy}(x,y)= f_x(x) f_y(y) = \frac{1}{2\Gamma(\frac{1}{2})^2}(xy)^{-\frac{1}{2}}e^{-\frac{x+y}{2}} =\frac{1}{2\pi}(xy)^{-\frac{1}{2}}e^{-\frac{x+y}{2}}$

Siano $A=xy$ e $B=x+y$ , abbiamo che:

$x = \frac{B+\sqrt{B^2-4A}}{2}$

$y = \frac{B-\sqrt{B^2-4A}}{2}$

o

$x = \frac{B-\sqrt{B^2-4A}}{2}$

$y = \frac{B+\sqrt{B^2-4A}}{2}$

Data la simmetria, possiamo prendere la prima coppia di soluzioni e moltiplicare il risultato per 2.

Lo jacobiano è:

$\begin{vmatrix} -(B^2-4A)^{-\frac{1}{2}} & \frac{1+B(B^2-4A)^{-\frac{1}{2}}}{2} \\ (B^2-4A)^{-\frac{1}{2}} & \frac{1-B(B^2-4A)^{-\frac{1}{2}}}{2} \\ \end{vmatrix} = (B^2-4A)^{-\frac{1}{2}}$

Possiamo quindi passare da $f(x,y)$ a $f(A,B)$ :

$f_{AB}(A,B)=2\times\frac{1}{2\pi}A^{-\frac{1}{2}}e^{-\frac{B}{2}}(B^2-4A)^{-\frac{1}{2}}$

La distribuzione marginale di $B = x+y$ è quindi:

$f_B(B)=2\times\frac{e^{-\frac{B}{2}}}{2\pi}\int_0^{\frac{B^2}{4}}A^{-\frac{1}{2}}(B^2-4A)^{-\frac{1}{2}}dA$

Ponendo $A=\frac{B^2}{4}\sin^2(t)$ , l'equazione diventa:

$f_B(B)=2\times\frac{e^{-\frac{B}{2}}}{2\pi}\int_0^{\frac{\pi}{2}}dA$

da cui:

$f_B(B)=\frac{e^{-\frac{B}{2}}}{2} = \frac{1}{2\Gamma(1)}B^{\frac{2}{2}-1}e^{-\frac{B}{2}}$

[modifica] Derivazione della funzione di densità per k gradi di libertà

Un campione di k realizzazioni $x_i$ di una variabile normale standard è rappresentabile come un punto in uno spazio k-dimensionale. La distribuzione della somma dei quadrati sarà:

$P(Q)dQ = \int_\Gamma \prod_{i=1}^k N(x_i)\,dx_i = \int_\Gamma \frac{e^{-(x_1^2 + x_2^2 + ... +x_k^2)/2}}{(2\pi)^{k/2}}\,dx_1dx_2...dx_k$

dove $N(x)$ è la funzione di densità di una distribuzione normale standard e $\Gamma$ è una superficie k-1-dimensionale nello spazio k-dimensionale per cui vale: