Teorema di Bayes

Formula del teorema di Bayes riprodotta in un'insegna a tubi fluorescenti negli uffici della sede di Cambridge della Autonomy Corporation

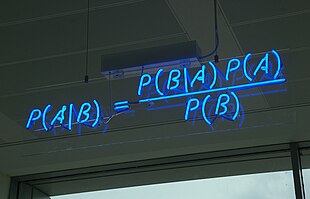
Il teorema di Bayes (pronuncia: /beɪz/, ; conosciuto anche come formula di Bayes o teorema della probabilità delle cause), enunciato da Thomas Bayes (1702-1761), discende da due risultati fondamentali della teoria della probabilità: il teorema della probabilità composta e il teorema della probabilità assoluta. Viene impiegato per calcolare la probabilità di una causa che ha provocato l'evento verificato.

Per esempio si può calcolare la probabilità che una certa persona soffra della malattia per cui ha eseguito il test diagnostico (nel caso in cui questo sia risultato negativo) o viceversa non sia affetta da tale malattia (nel caso in cui il test sia risultato positivo), conoscendo la frequenza con cui si presenta la malattia e la percentuale di efficacia del test diagnostico. Formalmente il teorema di Bayes è valido in tutte le interpretazioni della probabilità. In ogni caso, l'importanza di questo teorema per la statistica è tale che la divisione tra le due scuole (statistica bayesiana e statistica frequentista) nasce dall'interpretazione che si dà al teorema stesso.

Enunciato del teorema di Bayes

Considerando un insieme di alternative $A_{1},\ldots ,A_{n}$ che partizionano lo spazio degli eventi $\Omega$ (ossia $\ A_{i}\cap A_{j}=\varnothing$ per ogni $i\neq j$ e $\cup _{i=1}^{n}A_{i}=\Omega$) ed un evento $E\subset \Omega$ (di modo che l'evento $E$ implichi l'evento per cui si è avverata almeno un'alternativa) tale che $P(E)\neq 0$ si trova la seguente espressione per la probabilità condizionata:

$P(A_{i}|E)={\frac {P(E|A_{i})P(A_{i})}{P(E)}}={\frac {P(E|A_{i})P(A_{i})}{\sum _{j=1}^{n}P(E|A_{j})P(A_{j})}},$

dove:

• $P(A)$ è la probabilità a priori o probabilità marginale di $A.$ "A priori" significa che non tiene conto di nessuna informazione riguardo $E.$
• $P(A|E)$ è la probabilità condizionata di $A,$ noto $E.$ Viene anche chiamata probabilità a posteriori, visto che è derivata o dipende dallo specifico valore di $E.$
• $P(E|A)$ è la probabilità condizionata di $E,$ noto $A.$
• $P(E)$ è la probabilità a priori di $E,$ e funge da costante di normalizzazione.

Intuitivamente, il teorema descrive il modo in cui le opinioni nell'osservare $A$ siano arricchite dall'aver osservato l'evento $E.$

Un esempio

Si consideri una scuola che ha il 60% di studenti maschi e il 40% di studentesse femmine. Le studentesse indossano in egual numero gonne o pantaloni; gli studenti maschi indossano tutti quanti i pantaloni. Un osservatore, da lontano, nota un generico studente coi pantaloni. Qual è la probabilità che quello studente sia una femmina?

Il problema può essere risolto con il teorema di Bayes, ponendo l'evento $A$ che lo studente osservato sia femmina, e l'evento $B$ che lo studente osservato indossi i pantaloni. Per calcolare $P(A|B),$ dovremo sapere:

• $P(A),$ ossia la probabilità che lo studente sia femmina senza nessun'altra informazione. Dato che l'osservatore vede uno studente a caso, ciò significa che tutti gli studenti hanno la stessa probabilità di essere osservati. Essendo le studentesse il 40% del totale, la probabilità risulterà 2/5.
• $P(A'),$ ossia la probabilità che lo studente sia maschio senza nessun'altra informazione. Essendo $A'$ l'evento complementare di $A,$ risulta 3/5.
• $P(B|A),$ ossia la probabilità che uno studente femmina indossi i pantaloni (ossia la probabilità che, verificato l'evento che lo studente sia femmina, si verifichi l'evento che indossi i pantaloni). Poiché indossano gonne e pantaloni in egual numero, la probabilità sarà di 1/2.
• $P(B|A'),$ ossia la probabilità che uno studente indossi i pantaloni, noto che lo studente è maschio. Tutti gli studenti maschi indossano i pantaloni, quindi vale 1.
• $P(B),$ ossia la probabilità che uno studente qualsiasi (maschio o femmina) indossi i pantaloni. Poiché il numero di coloro che indossano i pantaloni è di 80 (60 maschi + 20 femmine) su 100 studenti fra maschi e femmine, la probabilità $P(B)$ è di 80/100 = 4/5.

Ciò detto, possiamo applicare il teorema:

$P(A|B)={\frac {P(B|A)P(A)}{P(B)}}={\frac {{\frac {1}{2}}\times {\frac {2}{5}}}{\frac {4}{5}}}={\frac {1}{4}}.$

C'è pertanto 1/4 di probabilità che lo studente sia femmina cioè 25%.

Derivazione del teorema

Teorema di Bayes. Ω è lo spazio delle misure: $A,$ non $A,$ $B,$ non $B.$ Il grafico evidenzia tutte le possibilità condizionate.

Il teorema deriva dalla definizione di probabilità condizionata. La probabilità di un evento $A,$ noto un evento $B,$ risulta:

$P(A|B)={\frac {P(A\cap B)}{P(B)}}.$

In modo analogo, la probabilità di un evento $B$ noto un evento $A$:

$P(B|A)={\frac {P(A\cap B)}{P(A)}}.$

Pertanto:

$P(A\cap B)=P(B|A)P(A).$

Sostituendo nella prima uguaglianza, si trova il teorema di Bayes:

$P(A|B)={\frac {P(A\cap B)}{P(B)}}={\frac {P(B|A)P(A)}{P(B)}}.$

Applicazioni

Applicazione al Problema di Monty Hall

Si supponga di partecipare a un gioco a premi, in cui si può scegliere fra tre porte: dietro una di esse c'è un'automobile, dietro le altre, due capre. Si sceglie una porta, diciamo la numero 1, e il conduttore del gioco a premi, che sa cosa si nasconde dietro ciascuna porta, ne apre un'altra, diciamo la 3, rivelando una capra. Quindi domanda: «Vorresti scegliere la numero 2?» Ti conviene cambiare la tua scelta originale?

Si potrebbe pensare che, con due porte chiuse, si abbia una probabilità 50:50 per ognuna, e che quindi non ci sia motivo di cambiare porta. Non è questo il caso. Chiamiamo l'evento che la macchina si trovi dietro una certa porta rispettivamente $A_{1},$ $A_{2}$ e $A_{3}.$

All'inizio, è ovvio che:

$P(A_{1})=P(A_{2})=P(A_{3})={\frac {1}{3}}.$

Come detto prima, la porta scelta è la numero 1. Chiamiamo $B$ l'evento "il presentatore apre la porta 3". Ora:

• Nel caso in cui la macchina sia dietro la porta 1, il presentatore sarà libero di scegliere la porta 2 o 3 casualmente. Pertanto, $P(B|A_{1})=1/2$
• Nel caso in cui la macchina sia dietro la porta 2, il presentatore sarà obbligato ad aprire la porta 3. Pertanto $P(B|A_{2})=1$
• Nel caso in cui la macchina sia dietro la porta 3, il presentatore sarà obbligato ad aprire la porta 2. Pertanto $P(B|A_{3})=0$

La probabilità a priori per l'evento $B$ è del 50%, infatti:

$P(B)=\sum _{i=1}^{3}P(B|A_{i})P(A_{i})={\frac {1}{2}}\cdot {\frac {1}{3}}+1\cdot {\frac {1}{3}}+0\cdot {\frac {1}{3}}={\frac {1}{2}},$

da cui:

${\begin{aligned}P(A_{1}|B)&={\frac {P(B|A_{1})P(A_{1})}{P(B)}}={\frac {{\frac {1}{2}}\cdot {\frac {1}{3}}}{\frac {1}{2}}}={\frac {1}{3}}\\P(A_{2}|B)&={\frac {P(B|A_{2})P(A_{2})}{P(B)}}={\frac {1\cdot {\frac {1}{3}}}{\frac {1}{2}}}={\frac {2}{3}}\\P(A_{3}|B)&={\frac {P(B|A_{3})P(A_{3})}{P(B)}}={\frac {0\cdot {\frac {1}{3}}}{\frac {1}{2}}}=0.\end{aligned}}$

Da ciò è evidente che si deve sempre cambiare con la porta 2.

Filtri bayesiani

I filtri bayesiani sono uno strumento utilizzato per combattere lo spam che deve il suo funzionamento proprio al teorema di Bayes. Un filtro bayesiano fa uso di un classificatore bayesiano per riconoscere se una certa sequenza di simboli (come una parola) si presenta spesso nei messaggi di spam, quindi applica l'inferenza bayesiana per calcolare la probabilità che un determinato messaggio sia spam.

Storia

Il teorema si chiama così in onore del reverendo Thomas Bayes (1702–1761), il quale studiò come calcolare una distribuzione per il parametro di una distribuzione binomiale. Un suo amico, Richard Price, pubblicò il lavoro nel 1763, dopo la morte di Bayes, nell'articolo Essay Towards Solving a Problem in the Doctrine of Chances. Alcuni anni dopo (nel 1774) viene formulato da Pierre Simon Laplace che probabilmente non era a conoscenza del lavoro di Bayes.

Una ricerca pubblicata nel 1983 da parte dal professore di statistica Stephen Stigler, sembrerebbe suggerire che il teorema di Bayes sia stato scoperto dal matematico inglese Nicholas Saunderson (1682-1739) anni prima di Bayes.

La scoperta del teorema di Bayes rimane un argomento controverso nella storia della matematica. Sebbene sia certo che sia stato scoperto prima dell'epoca di Thomas Bayes, ci sono diversi contendenti per la priorità, tra cui Saunderson. All'epoca, gran parte della ricerca matematica veniva svolta attraverso lo scambio di lettere private e discussioni verbali, piuttosto che attraverso le pubblicazioni. Lo storico della statistica Stephen Stigler ha concluso che Saunderson era lo scopritore più probabile dopo aver cercato di rintracciare alcune di queste lettere e discussioni, ma è stato contestato da altri statistici.

Bibliografia

Versioni saggistiche

• Thomas Bayes (1763), An Essay towards solving a Problem in the Doctrine of Chances. By the late Rev. Mr. Bayes, F. R. S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S., Philosophical Transactions, Giving Some Account of the Present Undertakings, Studies and Labours of the Ingenious in Many Considerable Parts of the World, 53:370–418.
• Thomas Bayes (1763/1958), Studies in the History of Probability and Statistics: IX. Thomas Bayes' Essay Towards Solving a Problem in the Doctrine of Chances, Biometrika 45:296–315. (Bayes' essay in modernized notation).

Commenti

• G. A. Barnard, Studies in the History of Probability and Statistics: IX. Thomas Bayes' Essay Towards Solving a Problem in the Doctrine of Chances, Biometrika 45:293–295, 1958
• Daniel Covarrubias, An Essay Towards Solving a Problem in the Doctrine of Chances
• Stephen M. Stigler, Thomas Bayes' Bayesian Inference, Journal of the Royal Statistical Society, Series A, 145:250–258, 1982
• Isaac Todhunter, A History of the Mathematical Theory of Probability from the time of Pascal to that of Laplace, Macmillan, 1865. Ristampa 1949, 1956 by Chelsea e 2001 by Thoemmes.

Voci correlate

• Probabilità
• Probabilità condizionata
• Teorema della probabilità composta
• Teorema della probabilità assoluta
• Paradosso dei corvi
• Problema di Monty Hall
• Paradosso delle tre carte
• Paradosso dei due bambini
• Inferenza bayesiana
• Thomas Bayes
• Pierre Simon Laplace
• Diagnosi

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul teorema di Bayes

Collegamenti esterni

• Giacomo Aletti, Teorema di Bayes, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
• (EN) Richard Routledge, Bayes’s theorem, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Teorema di Bayes, su Stanford Encyclopedia of Philosophy.
• (EN) Eric W. Weisstein, Bayes' Theorem, su MathWorld, Wolfram Research.

Controllo di autorità	Thesaurus BNCF 73793 · GND (DE) 4144221-0