Dilatazione temporale gravitazionale
La dilatazione temporale gravitazionale o dilatazione gravitazionale del tempo è l'effetto per cui il tempo scorre a differenti velocità in regioni di diverso potenziale gravitazionale; minore è il potenziale gravitazionale (più vicino al centro di un oggetto massivo, per esempio sulla superficie terrestre), più lentamente scorrono gli orologi. Sulla Stazione Spaziale Internazionale, con un alto potenziale gravitazionale (lontano dal centro massivo) un orologio scorre velocemente. Albert Einstein in origine, previde questo effetto nella sua teoria della relatività e da allora è stato confermato dalle prove della relatività generale.
Ciò è stato dimostrato osservando che gli orologi atomici a differenti altitudini (e perciò a diverso potenziale gravitazionale) mostrano alla fine tempi differenti. Gli effetti rilevati in tali esperimenti sono estremamente piccoli, con differenze misurate in nanosecondi.
La dilatazione temporale gravitazionale venne descritta per la prima volta da Albert Einstein nel 1907[1] come una conseguenza della relatività ristretta nelle strutture accelerate di riferimento. Nella relatività generale, è considerata come la differenza nel passaggio di tempo proprio a posizioni diverse come descritte da un tensore metrico di spazio-tempo. L'esistenza della dilatazione temporale gravitazionale venne per la prima volta confermata direttamente dall'esperimento di Pound-Rebka.
Definizione[modifica | modifica wikitesto]
Gli orologi che sono distanti da corpi massivi (o che sono a potenziali gravitazionali più elevati) vanno più velocemente mentre gli orologi vicini ai corpi massivi (o che si trovano a potenziali gravitazionali più bassi) vanno più lentamente. Questo succede perché la dilatazione temporale gravitazionale si manifesta nei sistemi di riferimento accelerati o in virtù del principio di equivalenza nel campo gravitazionale di oggetti massivi.[2]
Si può inoltre manifestare tramite ogni altro tipo di sistema di riferimento accelerato come un autoveicolo in accelerazione o un razzo spaziale. Oggetti ruotanti come giostre e ruote panoramiche sono soggette alla dilatazione temporale gravitazionale per effetto del loro momento angolare.
Secondo la teoria della relatività generale, a causa del principio di equivalenza la massa inerziale e la massa gravitazionale sono identiche e tutti i sistemi di riferimento accelerati sono fisicamente equivalenti a un campo gravitazionale della stessa forza.[3] Una persona sulla superficie della Terra, ad esempio, sperimenterebbe lo stesso identico effetto di una persona che si trovasse in una navicella spaziale che accelera a 9,8 m/s² (l'accelerazione del campo gravitazionale terrestre).
Non tutti i campi gravitazionali sono "curvi" o "sferici"; alcuni sono piatti come nel caso di un autoveicolo o di un'astronave in accelerazione. Ogni tipo di carico g contribuisce alla dilatazione temporale gravitazionale.
- In una scatola accelerata, l'equazione rispetto a un osservatore di base arbitrario è , dove
- è la dilatazione temporale totale a una posizione distante,
- è l'accelerazione della scatola come misurato dall'osservatore di base, e
- è la distanza "verticale" tra gli osservatori.
- Quando è molto più piccolo di , può anche essere utilizzata l'approssimazione del "campo debole" lineare .
- Su un disco rotante quando l'osservatore di base è situato al centro del disco e ruota insieme ad esso (rendendo la loro osservazione dello spazio-tempo non inerziale), l'equazione è , dove
- è la distanza dal centro del disco (che è la posizione dell'osservatore di base), e
- è la velocità del momento angolare del disco.
- Non è un caso che in un sistema inerziale di riferimento questo diventa la nota dilatazione temporale della velocità ).
All'esterno di una sfera non rotante[modifica | modifica wikitesto]
Un'equazione comune utilizzata per determinare la dilatazione gravitazionale del tempo è derivata dalla metrica di Schwarzschild, la quale descrive lo spaziotempo in prossimità di un oggetto sfericamente simmetrico massivo non rotante. L'equazione è:
dove
- è il tempo proprio tra gli eventi A e B rispetto a un osservatore che scandisce lento (slow-ticking) all'interno di un campo gravitazionale,
- è la coordinata tempo tra gli eventi A e B rispetto a un osservatore che scandisce veloce (fast-ticking) a una distanza arbitrariamente grande dall'oggetto massivo (questo presume che l'osservatore che scandisce veloce stia utilizzando le coordinate di Schwarzschild, un sistema di coordinate dove un orologio a distanza infinita dalla sfera massiva scandisce il tempo a un secondo per secondo della coordinata tempo, mentre gli orologi più vicini lo scandirebbero a una velocità inferiore),
- è la costante di gravitazione universale,
- è la massa dell'oggetto che crea il campo gravitazionale,
- è la coordinata radiale dell'osservatore (analoga alla distanza classica dal centro dell'oggetto, ma è in effetti una coordinata di Schwarzschild),
- è la velocità della luce, e
- è definito come raggio di Schwarzschild di M. Se una massa collassa in modo che la sua superficie si trovi a meno di questa coordinata radiale (o, in altre parole, copre un'area inferiore a ), allora l'oggetto esiste dentro un buco nero.
Aspetti importanti[modifica | modifica wikitesto]
- Secondo la relatività generale, la dilatazione gravitazionale del tempo è collegata all'esistenza di un sistema di riferimento non inerziale. Pertanto tutti i fenomeni fisici in circostanze similari sono soggetti alla stessa dilatazione temporale in base al principio di equivalenza utilizzato dalla teoria generale della relatività.
- La velocità della luce in un luogo è sempre uguale a c secondo l'osservatore che vi si trova. La prospettiva dell'osservatore stazionario corrisponde al tempo proprio del luogo. Questo significa che ogni regione infinitesimale dello spazio-tempo può avere il suo tempo proprio che corrisponde alla dilatazione gravitazionale del tempo, dove la radiazione elettromagnetica e la materia possono in ugual modo essere influenzate, poiché sono fatte della stessa essenza (come dimostrato in molte verifiche che coinvolgono la famosa equazione ). E ciò indipendentemente dal fatto che le regioni siano occupate da un osservatore. Si può misurare un ritardo di tempo per i segnali diretti verso Venere che vengono curvati in prossimità del Sole, e poi rimbalzano verso la Terra, lungo più o meno un percorso simile. In questo caso non c'è violazione della velocità della luce, poiché ogni osservatore che osserva la velocità dei fotoni nella sua regione troverà che questi possiedono una velocità c, mentre la velocità con cui la luce copre il percorso oltre il Sole differirà da c.
- Se un osservatore fosse in grado di rilevare la luce in un luogo distante, remoto, che intercetta un osservatore lontano con tempo dilatato perché vicino a un corpo più massiccio, il primo osservatore rileverebbe che sia la luce distante sia l'osservatore lontano con tempo dilatato avranno un orologio con tempo proprio più lento rispetto alla luce che arriverebbe al primo osservatore con la velocità c, come tutta l'altra luce che egli realmente riesce a osservare. Quando anche la luce lontana alla fine intercetta il primo osservatore, anche questa luce verrà misurata alla velocità c dal primo osservatore.
Conferma sperimentale[modifica | modifica wikitesto]
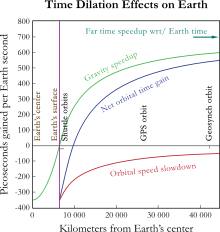
La dilatazione temporale gravitazionale è stata misurata sperimentalmente utilizzando orologi atomici posti su aerei. Gli orologi a bordo degli aerei erano leggermente più veloci rispetto a quelli al suolo. L'effetto è abbastanza significativo tanto che i satelliti artificiali del GPS hanno bisogno di sottoporre i loro orologi a correzione.[4]
In laboratorio sono state addirittura verificate sperimentalmente dilatazioni temporali dovute a differenze di altezza di meno di un metro.[5]
La dilatazione gravitazionale del tempo è stata confermata anche dall'esperimento di Pound e Rebka, dalle osservazioni degli spettri della nana bianca Sirio B e dagli esperimenti con segnali di tempo spediti al e dal lander marziano Viking 1.
Note[modifica | modifica wikitesto]
- ^ A. Einstein, Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen, Jahrbuch der Radioaktivität und Elektronik 4, 411–462 (1907); traduzione in inglese con On the relativity principle and the conclusions drawn from it, in "The Collected Papers", v.2, 433-484 (1989); anche in H M Schwartz, Einstein's comprehensive 1907 essay on relativity, part I, American Journal of Physics vol.45,no.6 (1977) pp.512-517; Part II in American Journal of Physics vol.45 no.9 (1977), pp.811-817; Part III in American Journal of Physics vol.45 no.10 (1977), pp.899-902, vedi parti I, II e III Archiviato il 28 novembre 2020 in Internet Archive..
- ^ John A. Auping, Proceedings of the International Conference on Two Cosmological Models, Plaza y Valdes, ISBN 6074025304, ISBN 9786074025309
- ^ Johan F. Prins, On Einstein's Non-Simultaneity, Length Contraction and Time-Dilation (PDF), su cathodixx.com.
- ^ (EN) Richard Wolfson, Simply Einstein, W. W. Norton & Co., 2003, p. 216, ISBN 0-393-05154-4.
- ^ C. W. Chou*, D. B. Hume, T. Rosenband e D. J. Wineland, Optical Clocks and Relativity, in Science, vol. 329, n. 5999, 24 settembre 2010, pp. 1630–1633.
Bibliografia[modifica | modifica wikitesto]
- (EN) Einstein, Albert. "Relativity: the Special and General Theory by Albert Einstein." Progetto Gutenberg. (Relativity: the Special and General Theory by Albert Einstein
- (EN) Einstein, Albert. The effect of gravity on light (1911), tradotto e ristampato in The Principle of Relativity (On the Influence of Gravitation on the Propagation of Light Archiviato il 2 giugno 2021 in Internet Archive.)
- (EN) Nave, C.R. "Gravity and the Photon." Hyperphysics. Black Hole. Gravity and the Photon. Escape Energy for Photon





















