Epiciclo e deferente

L'immagine mostra in modo schematico un ipotetico pianeta in orbita attorno alla Terra secondo la concezione tolemaica. L'orbita più grande (tratteggiata) è il deferente e X ne rappresenta il centro, quella più piccola l'epiciclo. Vicino al centro, ma da parti opposte, sono rappresentate la Terra e l'equante.

Con epiciclo si indica una circonferenza il cui centro è collocato sulla circonferenza di un cerchio di raggio maggiore detto deferente. Il termine viene dal greco ἐπίκυκλος ed è composto da ἐπί epì (sopra) e κυκλος kyklos (cerchio), quindi cerchio che sta sopra.

Tale schema fu ideato nel III secolo a.C. da Apollonio di Perga per descrivere il moto apparente dei pianeti sulla volta celeste. In tale modello le orbite planetarie sono rappresentate come un moto composto della rivoluzione del pianeta lungo l'epiciclo e di quest'ultimo lungo il deferente.

Lo schema epiciclo/deferente fu utilizzato da quasi tutti gli astronomi greci successivi e definitivamente adottato dalla cultura antica e medievale (islamica e cristiana) per l'influenza dell'Almagesto di Claudio Tolomeo. Anche Copernico vi fece ricorso, ad esempio per descrivere il moto della Luna tramite un deferente e due epicicli.

Storia

Moto retrogrado apparente di Marte nella costellazione dell'Acquario, come poteva essere visto dalla Terra nell'estate del 2003.

Il modello a sfere omocentriche di Eudosso di Cnido, adottato e promosso da Aristotele, descriveva il moto dei pianeti in modo grossolano. Non poteva spiegare le variazioni di luminosità dei pianeti, causate in realtà dalla loro distanza variabile dalla Terra, e soprattutto non dava pienamente ragione del loro misterioso moto retrogrado apparente (particolarmente ampio quello di Marte).

Anche la durata dell'anno solare non era suddivisa esattamente in quattro parti uguali da equinozi e solstizi. Questo fatto era stato notato da Metone e da Euctemone sin dal 430 a.C. Una misura precisa, fatta da Ipparco, trovò che il semestre estivo durava quasi nove giorni in più di quello invernale. Dato che il moto del Sole era ritenuto circolare uniforme per motivi filosofici (cfr. De caelo), vi si pose rimedio assumendo che la Terra non si trovasse esattamente al centro della sfera celeste occupata dal Sole, ma fosse leggermente eccentrica. Il trucco funzionava proprio perché l'orbita apparente del Sole è ellittica e la Terra è eccentrica, in quanto ne occupa uno dei fuochi.

L'eccentricità dell'orbita, però, non era in grado di spiegare il moto retrogrado apparente dei pianeti e le variazioni della loro luminosità (particolarmente intense quelle di Venere e Marte). Apollonio di Perga, quindi, introdusse il modello deferente/epiciclo, che, come egli osservò, costituisce una generalizzazione del modello dell'orbita circolare eccentrica da lui utilizzato per descrivere il moto solare.

La teoria trovò il suo più grande sostenitore in Claudio Tolomeo (II secolo d.C.), che lo perfezionò, sfruttando le conoscenze e le osservazioni di Ipparco di Nicea (II secolo a.C.). La fortuna dell'Almagesto, la principale opera astronomica di Tolomeo, diffuse la teoria degli epicicli in Oriente come in Occidente.

I filosofi, tuttavia, non persero di vista la sua natura descrittiva, priva, cioè, di quello sforzo di interpretazione fisica sistematica che fece la fortuna del De caelo di Aristotele per quasi duemila anni. Tommaso d'Aquino, per esempio, osservò: «in astronomia si ammettono gli eccentrici e gli epicicli perché, accettata questa ipotesi, si può dare ragione della irregolarità che nel moto dei corpi celesti appaiono ai sensi; tuttavia tale argomento non è cogente, poiché forse [tali irregolarità] potrebbero essere spiegate anche ammettendo un'altra ipotesi.». Questa affermazione di Tommaso illustra perché la Chiesa cattolica fu molto aperta al copernicanesimo, almeno sino al 1609. La posizione delle Chiesa s'irrigidì dal 1609, quando Galileo Galilei mostrò, con l'osservazione delle fasi di Venere fatta mediante il cannocchiale, la fallacia del sistema geocentrico, sostenendo inoltre la teoria eliocentrica come fisicamente vera, anziché mera ipotesi matematica atta a “salvare le apparenze” (spiegare e prevedere i moti apparenti): all'epoca di Galileo, infatti, la corrispondenza della teoria eliocentrica alla realtà fisica non poteva ancora essere dimostrata con prove sperimentali.

Descrizione del moto tramite deferente ed epicicli

Si osservi che convenzionalmente il deferente è il cerchio il cui raggio è il maggiore, ma in base alla regola del parallelogramma il moto risultante del pianeta resterebbe invariato anche se si utilizzasse come deferente il cerchio col raggio minore.

Il motivo per cui il cerchio maggiore è quello deferente deve cercarsi nella rappresentazione concettuale che i filosofi si facevano dello schema di calcolo proposto da Apollonio. Il deferente non era una linea immaginaria ma una porzione solida di cielo, che si estendeva approssimativamente fra il perigeo e l'apogeo del pianeta. In questa porzione era rigidamente fissato l'epiciclo come un castone in un anello. Rispetto ad un riferimento esterno, quindi, l'epiciclo ruotava rigidamente assieme al deferente.

Il moto di rotazione lungo le circonferenze era inizialmente ipotizzato avvenire con velocità angolare uniforme, ma il confronto con l'osservazione astronomica impose di elaborare regole più complicate (vedi equante). Il moto risultante è un moto complesso che descrive con buona approssimazione il moto dei pianeti nella volta celeste come appare a un osservatore posto sulla Terra.

Efficacia nella descrizione delle orbite planetarie

Il moltiplicarsi degli epicicli nel tentativo di riprodurre il moto dei corpi celesti viene talvolta presentato ironicamente, ma ha trovato con lo sviluppo della matematica una giustificazione teorica. A partire dagli studi di Giovanni Schiaparelli nel 1874 ci si è resi conto che vi è "una completa equivalenza fra la rappresentazione dei moti quasi-periodici per mezzo di una trasformata di Fourier e quella in termini di epicicli".

Le potenzialità del modello epiciclo/deferente per la rappresentazione dei moti astronomici nella loro massima generalità possono essere colte anche in modo semplice considerando un solo epiciclo. A questo scopo occorre scrivere le coordinate del punto mobile (il pianeta) addizionando le equazioni parametriche dei due cerchi:

$x=R\cos \omega t+r\cos \phi t$

$y=R\sin \omega t+r\sin \phi t$

in cui $R$ e $r$ sono i raggi rispettivamente del deferente e dell'epiciclo e $\omega$ e $\phi$ le corrispondenti velocità angolari. Si osservi, come sopra anticipato, che la formulazione matematica è semplicemente additiva (non c'è nessuna distinzione formale fra epiciclo e deferente) e aperta all'aggiunta di altri moti circolari. Si osservi inoltre:

• Come aveva osservato Claudio Tolomeo, con opportuna scelta dei parametri il sistema epiciclo/deferente può rappresentare anche un semplice cerchio eccentrico (nella presente notazione basta porre $\phi =0$ e si ottiene un cerchio di eccentricità $r$).
• Il movimento di un qualsiasi pianeta relativamente alla Terra può essere agevolmente descritto (nell'approssimazione di orbite circolari) assegnando a un cerchio i valori che oggi conosciamo caratteristici del moto apparente del Sole attorno alla Terra e all'altro i valori caratteristici del moto del pianeta attorno al Sole. In altre parole il sistema copernicano risulta essere semplicemente un cambiamento di sistema di riferimento e descrive i moti relativamente alla Terra in modo esattamente uguale a come potrebbe essere descritto con deferente ed epicicli.
• Se poi si sceglie esattamente $\phi =-\omega$ si ottiene un moto ellittico di semiassi:

$a=R+r$

$b=R-r$.

Il moto ellittico di un corpo celeste attorno ad un altro posto in uno dei fuochi (prima legge di Keplero) potrebbe essere descritto esattamente tramite un solo epiciclo relativo a un deferente eccentrico.

• Se, invece, fra $\phi$ e $-\omega$ vi fosse una piccola differenza, l'ellisse non si chiuderebbe perfettamente al termine di un ciclo e la curva risultante descriverebbe anche il moto di rotazione dell'asse degli apsidi, un fenomeno osservato nel moto lunare sin dai tempi di Ipparco.

In conclusione il sistema deferente/epiciclo non pone alcun limite alla modellazione delle orbite dei corpi del sistema solare relativamente alla Terra. In altre parole la teoria che i moti celesti possano essere modellati tramite deferente ed epicicli non è falsificabile perché priva di contenuto fisico significativo.

La scoperta, però, che il moto retrogrado di un pianeta potesse essere descritto con un solo epiciclo e che con pochi altri potessero essere modellate tutte le caratteristiche dei moti planetari misurabili dagli astronomi antichi, fu un evento storico di primaria importanza, senza il quale il sistema eliocentrico non avrebbe mai potuto imporsi.

Il geo-eliocentrismo di Tycho Brahe e la prima legge di Keplero risolvono elegantemente il problema di identificare i numerosi parametri con cui caratterizzare gli epicicli. Furono i dati accuratissimi raccolti da Tycho Brahe oltre diciotto secoli dopo a rendere obsoleto, non perché erroneo ma perché farraginoso, il modello cinematico proposto da Apollonio di Perga e perfezionato da Claudio Tolomeo.

Rapporti con altre teorie astronomiche

L'idea di una rotazione attorno a un centro, che a sua volta ruota attorno a un altro punto, è stata molto importante per lo sviluppo dell'astronomia.

Moti lineari

Costruzione del moto lineare secondo Tusi: ogni punto del cerchio rosso percorre armonicamente un diverso diametro del cerchio maggiore.

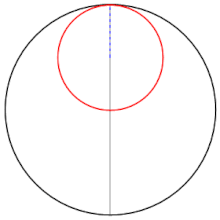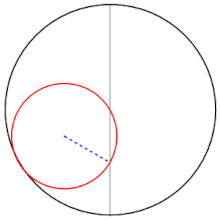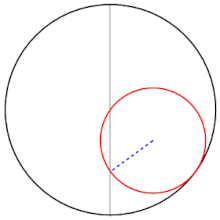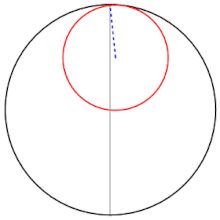
I corpi celesti presentano anche moti di oscillazione lungo una sola direzione: è il caso ad esempio dei moti in latitudine della Luna e dei pianeti. La possibilità di rappresentarli tramite due rotazioni fu suggerita nel 1247 dal grande astronomo persiano Nasir al-Din al-Tusi e fu utilizzata in Occidente per la prima volta da Nicole Oresme nelle sue Questiones sul Tractatus de Sphaera di Giovanni Sacrobosco (scritte prima del 1362). Anche Copernico vi fece ricorso nel IV capitolo del III libro. Non è chiaro in che misura le loro idee beneficiarono del lavoro di Tusi e se tutti o alcuni di loro trassero ispirazione da Proclo, che nel suo Commentario al primo libro di Euclide mostrò come due traslazioni possono dare luogo a un moto circolare..

L'idea può essere spiegata facilmente, assumendo nella formulazione soprastante:

$r=R$

$\phi =-\omega$

valori per i quali il semiasse minore si riduce a zero e si ottiene un moto lineare armonico lungo un diametro del deferente, ma di ampiezza totale $4R$.

Nel descrivere la propria costruzione geometrica Tusi restò ancorato alla terminologia dell'astronomia greca per cui il cerchio minore subiva per trascinamento la rotazione del cerchio maggiore e perciò doveva essere dotato di una velocità angolare doppia nell'altro verso (nella descrizione precedente, invece, le due velocità sono contrarie ma uguali). Una descrizione equivalente ma più elegante (non dovuta a Tusi) visualizza l'epiciclo come un cerchio che rotola entro una circonferenza di raggio doppio. La costruzione di Tusi risulta allora un caso particolare di una famiglia di curve dette ipotrocoidi e studiate non solo in geometria ma anche in meccanica (cfr. rulletta).

Sistema ticoniano e sistema eliocentrico

La combinazione di due moti di rotazione ha anche intrecciato lo sviluppo del geocentrismo con quello dell'eliocentrismo. Nel IV secolo Eraclide Pontico per primo intuì la possibilità che Mercurio e Venere ruotassero attorno al Sole, il quale a sua volta ruotava attorno alla Terra. Questa teoria è incoraggiata dal fatto che la massima distanza angolare dal Sole dei due pianeti visti dalla Terra (la cosiddetta "elongazione") è limitata a poche decine di gradi. L'ipotesi, quindi, non venne dimenticata e fu ripresa successivamente da Marziano Capella. Troverà il suo sviluppo completo nel modello proposto da Tycho Brahe venti secoli dopo.

Parallelamente l'ipotesi di Eraclide diede luogo allo sviluppo del sistema copernicano. Nel III secolo, poco dopo Eraclide, Aristarco di Samo pose sul Sole il punto d'osservazione (fisso per definizione), proponendo per primo l'eliocentrismo vero e proprio. Tuttavia, il moto eliocentrico dei pianeti visto dalla Terra è ancora una rotazione combinata con un'altra rotazione.

Voci correlate

• Ipotrocoide
• Ipocicloide
• Cicloide
• Epicicloide
• Trocoide
• Epitrocoide

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «epiciclo»
• Wikimedia Commons contiene immagini o altri file su epiciclo

Collegamenti esterni

• (EN) epicycle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.