Equante
Nell'astronomia planetaria l'equante (in latino punctum aequans) è un ipotetico punto posto sulla linea degli apsidi di un pianeta caratterizzato dal fatto che la velocità angolare del pianeta misurata dal punto equante è costante nel tempo.
Nella storia dell'astronomia il metodo dell'equante è un metodo sviluppato nel II secolo d.C. da Claudio Tolomeo per descrivere come uniforme la velocità angolare con cui i pianeti percorrono la loro orbita. L'introduzione di questa correzione è il principale contributo di Tolomeo alla descrizione dei moti planetari. In particolare il metodo compare per la prima volta nel V libro dell'Almagesto, dove è utilizzato per migliorare il modello dell'orbita lunare proposto da Ipparco. Tuttavia, il metodo di Tolomeo potrebbe essere solo un perfezionamento del "metodo dell'equante concentrico", presente in testi indiani del V-VII secolo d.C., ma forse merito di un astronomo greco posteriore a Ipparco e precedente Tolomeo.[1]
Storia[modifica | modifica wikitesto]
Secondo l'impostazione dell'universo geocentrico immaginata da Eudosso prima e Aristotele poi i corpi celesti dovevano compiere con velocità uniforme orbite circolari che mal si conciliavano con l'osservazione pratica. Il sistema geocentrico aristotelico, infatti, non poteva spiegare né la variazione di luminosità dei pianeti, dovuta alla variazione di distanza dalla Terra, né la variabilità della velocità angolare con cui il Sole e i pianeti sembravano percorrere l'eclittica. L'introduzione del sistema deferente/epiciclo da parte di Apollonio di Perga e di Ipparco e l'ipotesi che il centro della Terra fosse diverso dal centro del deferente (detto, in questo caso, eccentrico), resero variabile la distanza dei pianeti dalla Terra; il secondo problema fu risolto da Tolomeo con l'introduzione dell'equante.
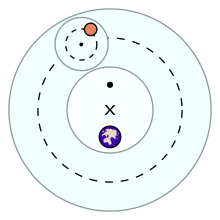
Prima di Tolomeo si era ipotizzato che il moto del Sole/pianeta lungo il deferente fosse circolare uniforme e apparisse non uniforme dalla Terra solo a causa della posizione del centro del deferente (eccentrico x), spostato rispetto a essa.
Tolomeo, però, si accorse che l'eccentricità necessaria perché il moto attorno al deferente risultasse uniforme avrebbe condotto a valutazioni erronee dei moti retrogradi dei pianeti. Probabilmente egli misurò la velocità angolare di Marte agli apsidi (il perielio e l'afelio), quando essa raggiunge rispettivamente il valore massimo e minimo, e verificò che le due velocità sarebbero apparse uguali (da ciò il nome "equante") solo da un punto diametralmente opposto alla Terra rispetto al centro del deferente.[2]
Infatti l'angolo α misurato al centro del deferente (eccentrico x) tra il raggio ruotante R del deferente e la linea congiungente equante • - eccentrico x - Terra[3] in funzione del tempo t è
dove Ω è la velocità angolare costante vista dal punto equante •, situato a una distanza E dall'eccentrico x.
Solo quando l'eccentrico x coincide con il punto equante • vale E = 0 e l'equazione precedente si riduce a quella di un moto circolare uniforme:
In testi indiani del V-VII secolo d.C. compare una versione semplificata del metodo dell'equante, detto "metodo concentrico dell'equante". In questo metodo, anch'esso probabilmente d'origine greca, il centro del deferente coincide con il centro della Terra (eccentricità nulla), mentre il punto equante, rispetto al quale il Sole/pianeta si muove di moto circolare uniforme, risulta non coincidente con essi.
L'esistenza di un punto equante non è imposta da ragioni fisiche, ma una scelta di taluni modelli astronomici. Il persiano Muʾayyad al-Dīn al-ʿUrḍī (1200 ca.-1266), che lavorò nell'osservatorio di Maragha in Persia, propose un metodo (noto come motto di Urdi) che consente di sostituire un equante con un epiciclo a esso equivalente. Il matematico e astronomo persiano Naṣīr al-Dīn al-Ṭūsī (1201-1274) inventò un altro metodo, che porta il suo nome, per eliminare equanti e consiste in una piccola circonferenza che ruota all'interno di un'altra dal diametro doppio. L'astronomo siriano Ibn al-Shatir (1304-1375), utilizzando il metodo di al-Tusi, riuscì a migliorare il sistema tolemaico: aggiungendo altri epicicli eliminò eccentrici ed equanti.[4]
Niccolò Copernico (1473-1543) basò il proprio rifiuto del sistema tolemaico su una ragione scientifica e una estetica: la ricerca di un'alternativa più elegante, di una soluzione più "bella". Per quanto riguarda la motivazione scientifica, la distanza tra la Terra e la Luna dipendeva, secondo Tolomeo, dalla fase di quest'ultima. Copernico eseguì, in vari momenti della sua vita, ripetute misurazioni della distanza della Luna, non trovando differenze significative al variare della fase lunare.[5] Per quanto concerne la motivazione estetica, Copernico eliminò il punto equante, da lui ritenuto artificioso e inutile in quanto non corrispondente ad alcun ente fisico identificabile. Conservò invece gli altri correttivi introdotti ad hoc da Tolomeo per spiegare le variazioni dimensionali e i moti retrogradi apparenti dei pianeti: gli epicicli, i deferenti e gli eccentrici.[6]
Note[modifica | modifica wikitesto]
- ^ Dennis Duke, An Interesting Property of the Equant, DIO, Dicembre 2008, p. 33
- ^ James Evans, On the function and the probable origin of Ptolemy's equant (PDF), in Am J Phys, vol. 52, n. 12, 18 aprile 1984, pp. 1080–1089, DOI:10.1119/1.13764. URL consultato il 29 agosto 2014.. In particolare p. 1088
- ^ Vedi Eccentrics, deferents, epicycles and equants (Mathpages) Figura 3
- ^ José Luis Huertas Díaz, Copernico. L'eliocentrismo. In giro con la Terra, RBA, 2014, pp. 86–87.
- ^ J.L. Huertas Díaz, Op. cit., p.59
- ^ Franco Piperno, Variazioni sul cielo. Il sistema eliocentrico di Copernico (1473-1543), su lcs.unical.it. URL consultato il 25 maggio 2016 (archiviato dall'url originale il 18 luglio 2016).
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su equante
Wikimedia Commons contiene immagini o altri file su equante
Collegamenti esterni[modifica | modifica wikitesto]
- Eccentrics, deferents, epicycles and equants (Mathpages), su mathpages.com.
- Ptolemaic System – at Rice University's Galileo Project
- Dennis Duke, An Interesting Property of the Equant, DIO, Dicembre 2008, pp. 24–37.

