Teoria delle rappresentazioni: differenze tra le versioni
Redirect a Rappresentazione dei gruppi |
cambio redirect errato in una voce Etichetta: Rimosso redirect |
||
| Riga 1: | Riga 1: | ||
[[File:Hexagon_reflections.svg|destra|miniatura|250x250px|La teoria delle rappresentazioni studia come le strutture algebriche "agiscono" sugli oggetti. Un semplice esempio è come le [[Gruppo diedrale|simmetrie dei poligoni regolari]], costituiti da riflessioni e rotazioni, trasformano il poligono.]] |
|||
#REDIRECT [[Rappresentazione dei gruppi]] |
|||
La '''teoria delle rappresentazioni''' è una branca della [[matematica]] che studia le [[struttura algebrica|strutture algebriche]] [[algebra astratta|astratte]] "rappresentando" i loro elementi come [[trasformazione lineare|trasformazioni lineari]] di [[spazio vettoriale|spazi vettoriali]]<ref>{{Cite web|url=https://mathvault.ca/math-glossary/#representation|title=The Definitive Glossary of Higher Mathematical Jargon — Mathematical Representation|date=2019-08-01|website=Math Vault|language=en-US|access-date=2019-12-09}}</ref> e studiando i [[modulo (algebra)|moduli]] su queste strutture algebriche astratte.<ref>{{Cite web|url=https://ncatlab.org/nlab/show/representation+theory|title=representation theory in nLab|website=ncatlab.org|access-date=2019-12-09}}</ref> Sostanzialmente una rappresentazione rende più concreto un oggetto algebrico astratto descrivendo i suoi elementi mediante [[matrice|matrici]]. La teoria delle matrici e delle trasformazioni lineari è ben nota, quindi rappresentazioni di oggetti più astratti in termini di oggetti familiari dell'algebra lineare semplifica i calcoli e aiuta a capire e determinare le proprietà di questi oggetti astratti. |
|||
Un [[gruppo di Lie]] è un gruppo che è anche una [[varietà differenziabile]]. Molti gruppi classici di matrici sui numeri reali o complessi sono gruppi di Lie. Molti gruppi importanti in fisica e chimica sono gruppi di Lie e la loro teoria delle rappresentazioni è cruciale per l'applicazione della [[teoria dei gruppi]] in questi campi. |
|||
La teoria delle rappresentazioni è uno strumento utile in quanto riduce problemi di [[algebra astratta]] a problemi di [[algebra lineare]]. Inoltre lo spazio vettoriale su cui (per esempio) un gruppo è rappresentato può essere di dimensione infinita. Se questo, per esempio, è uno [[spazio di Hilbert]], allora i metodi dell'[[analisi funzionale]] possono essere applicati alla [[teoria dei gruppi]].<ref>{{Harvnb|Sally|Vogan|1989}}.</ref><ref name=":12">{{Cite web|url=https://math.berkeley.edu/~teleman/math/RepThry.pdf|title=Representation Theory|last=Teleman|first=Constantin|date=2005|website=math.berkeley.edu|access-date=2019-12-09}}</ref> La teoria delle rappresentazioni è importante anche in [[fisica]] poiché, per esempio, descrive come il [[gruppo di simmetria]] di un sistema fisico influenza le soluzioni delle equazioni che descrivono il sistema.<ref name="Sternberg2">{{Harvnb|Sternberg|1994}}.</ref> |
|||
La teoria delle rappresentazioni è presente in tutti i campi della matematica per due ragioni. In primo luogo, le applicazioni della teoria delle rappresentazioni sono diverse; oltre al suo impatto sull'algebra, la teoria delle rappresentazioni: |
|||
* rende più chiara e generalizza l'[[analisi di Fourier]] tramite l'[[analisi armonica]]; |
|||
* è connessa alla [[geometria]] tramite la [[Teoria geometrica degli invarianti|teoria degli invarianti]] e il [[programma di Erlangen]]; |
|||
* ha un impatto sulla [[teoria dei numeri]] tramite le [[Forma automorfa|forme automorfe]] e il [[programma Langlands]]. |
|||
In secondo luogo, ci sono diversi approcci alla teoria delle rappresentazioni. Gli stessi oggetti possono essere studiati usando metodi della [[geometria algebrica]], della [[Modulo (algebra)|teoria dei moduli]], della [[teoria analitica dei numeri]], della [[geometria differenziale]], della [[teoria degli operatori]], della [[combinatoria algebrica]] e della [[topologia]]. |
|||
Il successo della teoria delle rappresentazioni ha portato a numerose generalizzazioni. Una delle versioni più generali si ha nella [[teoria delle categorie]]. Gli oggetti algebrici a cui si applica la teoria delle rappresentazioni possono essere visti come particolari tipi di categorie e le rappresentazioni come [[Funtore (matematica)|funtori]] dalla categoria degli oggetti algebrici considerati alla categoria degli spazi vettoriali.<ref name=":0">{{Cita web|url=http://www-math.mit.edu/~etingof/replect.pdf|sito=www-math.mit.edu|dataaccesso=2019-12-09}}</ref> Questa descrizione indica due ovvie generalizzazioni: primo, gli oggetti algebrici possono essere sostituiti da categorie più generali; secondo, la categoria di arrivo degli spazi vettoriali può essere sostituita da altre categorie ben studiate. |
|||
== Definizioni e concetti == |
|||
Sia <math>V</math> uno [[spazio vettoriale]] su un [[Campo (matematica)|campo]] <math>F</math>. Per esempio supponiamo che <math>V</math> sia <math>\R^n</math> o <math>\Complex^n,</math> lo spazio vettoriale <math>n</math>-dimensionale standard sui [[numero reale|reali]] o sui [[numero complesso|complessi]], rispettivamente. In questo caso, l'idea della teoria delle rappresentazioni è lavorare con l'[[algebra astratta]] in concreto usando le [[Matrice|matrici]] <math>n\times n</math> di numeri reali o complessi. |
|||
Ci sono tre tipi principali di [[Algebra|oggetti algebrici]] su cui può essere fatto: [[Gruppo (matematica)|gruppi]], [[algebra associativa|algebre associative]] e [[Algebra di Lie|algebre di Lie]].<ref name=":0">{{Cita web|url=http://www-math.mit.edu/~etingof/replect.pdf|sito=www-math.mit.edu|dataaccesso=2019-12-09}}</ref> |
|||
* L'insieme di tutte le [[Matrice invertibile|matrici invertibili]] di ordine <math>n</math> è un gruppo rispetto alla [[moltiplicazione di matrici]] e la [[Rappresentazione dei gruppi|teoria delle rappresentazioni dei gruppi]] analizza un gruppo descrivendo ("rappresentando") i suoi elementi in termini di matrici invertibili. |
|||
* L'addizione e la moltiplicazione di matrici rendono l'insieme di tutte le matrici <math>n\times n</math> un'algebra associativa, e quindi esiste una corrispondente teoria delle rappresentazioni delle algebre associative. |
|||
* Se sostituiamo la moltiplicazione di matrici <math>MN</math> con il [[Commutatore (matematica)|commutatore]] di matrici <math>MN-NM,</math> l'insieme delle matrici di ordine <math>n</math> diventa invece un'algebra di Lie, portando a una teoria delle rappresentazioni delle algebre di Lie. |
|||
Questo si generalizza a qualsiasi campo <math>F</math> e qualsiasi spazio vettoriale <math>V</math> su <math>F,</math> sostituendo le matrici con le [[Trasformazione lineare|funzioni lineari]] e la moltiplicazione di matrici con la [[Composizione di funzioni|composizione]]; cioè, per ogni spazio vettoriale <math>V</math> su <math>F</math> esiste un gruppo [[Gruppo generale lineare|GL(''V'',''F'')]] di [[Trasformazione lineare|automorfismi]] di <math>V,</math> essite un'algebra associativa <math>\mathrm{End}_F(V)</math> di tutti endomorfismi di <math>V,</math> e una corrispondente algebra di Lie <math>\mathfrak{gl}(V,F).</math> |
|||
=== Definizione === |
|||
Ci sono due modi per definire una rappresentazione. Il primo utilizza l'idea di [[azione di gruppo]], generalizzando il modo in cui le matrici agiscono sui vettori colonna mediante la moltiplicazione matriciale. Una rappresentazione di un [[Gruppo (algebra)|gruppo]] <math>G</math> o di un'algebra (associativa o di Lie) <math>A</math> su uno spazio vettoriale <math>V</math> è una funzione |
|||
:<math> \Phi\colon G\times V \to V, \quad\text{oppure}\quad \Phi\colon A\times V \to V,</math> |
|||
con due proprietà. Primo, per ogni <math>g\in G</math> (o <math>a\in A</math>), la funzione |
|||
:<math> \begin{align}\Phi(g)\colon V& \to V\\ |
|||
v & \mapsto \Phi(g, v)\end{align}</math> |
|||
è lineare (su <math>F</math>). Secondo, se introduciamo la notazione <math>g\cdot v</math> per <math>\Phi(g, v),</math> per ogni <math>g_1,g_2\in G</math> e <math>v\in V</math>: |
|||
:<math> (1)\quad e \cdot v = v,</math> |
|||
:<math> (2)\quad g_1\cdot (g_2 \cdot v) = (g_1g_2) \cdot v,</math> |
|||
dove <math>e</math> è l'[[elemento neutro]] di <math>G</math> e <math>g_1g_2</math> è il prodotto in <math>G.</math> Il requisito per le algebre associative è analogo, tranne per il fatto che le algebre associative non hanno sempre un elemento neutro, nel qual caso l'equazione (1) viene ignorata. L'equazione (2) è un'espressione astratta dell'associatività della moltiplicazione di matrici. Questo non vale per il commutatore di matrici e inoltre non vi è alcun elemento neutro per il commutatore. Quindi per le algebre di Lie, l'unico requisito è che per ogni <math>x_1,x_2\in A</math> e <math>v\in V</math>: |
|||
:<math> (2')\quad x_1\cdot (x_2 \cdot v) - x_2\cdot (x_1 \cdot v) = [x_1,x_2] \cdot v,</math> |
|||
dove <math>[x_1,x_2]</math> è la [[Algebra di Lie|parentesi di Lie]], che generalizza il commutatore di matrici <math>MN-NM.</math> |
|||
Il secondo modo per definire una rappresentazione è tramite la funzione <math>\varphi</math> che manda <math>g\in G</math> in una funzione lineare <math>\varphi(g)\colon V\to V,</math> che soddisfa |
|||
:<math>\varphi(g_1 g_2) = \varphi(g_1)\circ \varphi(g_2), \quad \text{per ogni }g_1,g_2 \in G,</math> |
|||
e analogamente negli altri casi. Questo approccio è più conciso e più astratto. Da questo punto di vista: |
|||
* una rappresentazione di un gruppo <math>G</math> su uno spazio vettoriale <math>V</math> è un [[omomorfismo di gruppi]] <math>\varphi\colon G\to \mathrm{GL}(V,F)</math>;<ref name=":1">{{Cita web|url=https://math.berkeley.edu/~teleman/math/RepThry.pdf|sito=math.berkeley.edu|dataaccesso=2019-12-09}}</ref> |
|||
* una rappresentazione di un'algebra associativa <math>A</math> su uno spazio vettoriale <math>V</math> è un [[omomorfismo di algebre]] <math>\varphi\colon A\to \mathrm{End}_F(V)</math>; |
|||
* una rappresentazione di un'algebra di Lie <math>\mathfrak{a}</math> su uno spazio vettoriale <math>V</math> è un [[Algebra di Lie|omomorfismo di algebre di Lie]] <math>\varphi\colon \mathfrak{a}\to \mathfrak{gl}(V,F)</math>. |
|||
=== Terminologia === |
|||
Lo spazio vettoriale <math>V</math> è chiamato '''spazio''' di ''rappresentazione di <math>\varphi</math>'' e la sua [[Dimensione (spazio vettoriale)|dimensione]] (se finita) è chiamata '''dimensione''' della rappresentazione (a volte ''grado'', come in <ref>Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Springer-Verlag, ISBN 978-0387901909</ref>). È anche pratica comune riferirsi a <math>V</math> stesso come alla rappresentazione quando l'omomorfismo <math>\varphi</math> è chiaro dal contesto; altrimenti la notazione <math>(V,\varphi)</math> può essere usata per indicare una rappresentazione. |
|||
Quando <math>V</math> è di dimensione finita <math>n,</math> si può scegliere una [[Base (algebra lineare)|base]] per <math>V</math> per identificare <math>V</math> con <math>F^n,</math> e quindi recuperare una rappresentazione matriciale con elementi nel campo <math>F.</math> |
|||
Una rappresentazione ''effettiva'' o ''fedele'' è una rappresentazione <math>(V,\varphi),</math> per la quale l'omomorfismo <math>\varphi</math> è [[Funzione iniettiva|iniettivo]]. |
|||
=== Funzioni equivarianti e isomorfismi === |
|||
Se <math>V</math> e <math>W</math> sono spazi vettoriali su <math>F,</math> con rappresentazioni <math>\varphi</math> e <math>\psi</math> di un gruppo <math>G,</math> allora una '''funzione equivariante''' da <math>V</math> a <math>W</math> è una funzione lineare <math>\alpha\colon V\to W</math> tale che |
|||
:<math> \alpha( g\cdot v ) = g \cdot \alpha(v),</math> |
|||
per ogni <math>g\in G</math> e <math>v\in V.</math> In termini di <math>\varphi\colon G\to \mathrm{GL}(V)</math> e <math>\psi\colon G\to \mathrm{GL}(W),</math> questo significa |
|||
:<math>\alpha\circ \varphi(g) = \psi(g)\circ \alpha,</math> |
|||
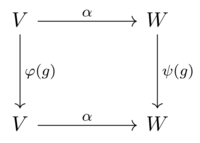
per ogni <math>g\in G,</math> cioè, il [[Diagramma commutativo|diagramma]] seguente commuta: |
|||
:[[Image:Equivariant map commutative diagram.png|200px]] |
|||
Le funzioni equivarianti per le rappresentazioni di un'algebra associativa o di Lie sono definite in modo simile. Se <math>\alpha</math> è invertibile, allora si dice che è un [[isomorfismo]], nel qual caso <math>V</math> e <math>W</math> (o, più precisamente, <math>\varphi</math> e <math>\psi</math>) sono ''rappresentazioni isomorfe'', anche dette ''rappresentazioni equivalenti''. Una funzione equivariante è spesso chiamata ''funzione intrecciata'' delle rappresentazioni. Inoltre, nel caso di un gruppo <math>G,</math> a volte è chiamato <math>G</math>-funzione. |
|||
Le rappresentazioni isomorfe sono, per scopi pratici, "le stesse"; forniscono le stesse informazioni sul gruppo o sull'algebra rappresentati. La teoria delle rappresentazioni cerca quindi di classificare le rappresentazioni a meno di isomorfismo. |
|||
=== Sottorappresentazioni, quozienti e rappresentazioni irriducibili === |
|||
Se <math>(V,\psi)</math> è una rappresentazione di un gruppo <math>G,</math> e <math>W</math> è un sottospazio vettoriale di <math>V</math> che è preservato dall'azione di <math>G,</math> ossia per ogni <math>w \in W</math> e <math>g\in G,</math> si ha <math>g\cdot w \in W</math> ([[Jean-Pierre Serre|Serre]] chiama <math>W</math> ''stabile rispetto a'' <math>G</math>), quindi <math>W</math> è chiamata ''sottorappresentazione''. Definendo |
|||
:<math>\phi\colon G \to \text{Aut}(W),</math> |
|||
dove <math>\phi(g)</math> è la restrizione di <math>\psi(g)</math> per <math>W,</math> allora <math>(W,\phi)</math> è una rappresentazione di <math>G</math> e l'inclusione di <math>W \hookrightarrow V</math> è una funzione equivariante. Anche lo [[Spazio vettoriale quoziente|spazio quoziente]] <math>V/W</math> ha una struttura di rappresentazione di <math>G</math>. Se <math>V</math> ha esattamente due sottorappresentazioni, vale a dire il sottospazio banale <math>\{0\}</math> e <math>V</math> stessa, allora la rappresentazione è detta ''irriducibile''. Se <math>V</math> ha una sottorappresentazione non banale propria, si dice che la rappresentazione è ''riducibile''.<ref>La rappresentazione {0} di dimensione zero è considerata non essere riducibile né irriducibile, analogamente al numero 1 che non è considerato compost né [[Numero primo|primo]].</ref> La definizione di rappresentazione irriducibile implica il [[lemma di Schur]]: una funzione equivariante |
|||
:<math>\alpha: (V,\psi)\to (V',\psi')</math> |
|||
tra rappresentazioni irriducibili o è la [[0 (numero)|funzione zero]] o è un isomorfismo, poiché il nucleo e l'[[Immagine (matematica)|immagine]] sono sottorappresentazioni. In particolare, quando <math>V = V',</math> questo mostra che gli [[Endomorfismo|endomorfismi]] equivarianti di <math>V</math> formano un'[[Algebra di divisione|algebra di divisione associativa]] sul campo sottostante <math>F.</math> Se <math>F</math> è [[Campo algebricamente chiuso|algebricamente chiuso]], gli unici endomorfismi equivarianti di una rappresentazione irriducibile sono i multipli scalari dell'identità. Le rappresentazioni irriducibili sono gli elementi costitutivi della teoria delle rappresentazioni per molti gruppi: se una rappresentazione <math>V</math> non è irriducibile, allora è costruita apartire da una sottorappresentazione e da un quoziente entrambi, in un certo senso, "più semplici". Per esempio, se <math>V</math> è di dimensione finita, allora sia la sottorappresentazione che il quoziente hanno dimensione minore. Ci sono controesempi in cui una rappresentazione ha una sottorappresentazione, ma ha solo una componente irriducibile non banale. Ad esempio, il gruppo additivo <math>(\mathbb{R},+)</math> ha una rappresentazione bidimensionale |
|||
:<math>\phi(a) = \begin{bmatrix} |
|||
1 & a \\ |
|||
0 & 1 |
|||
\end{bmatrix}.</math> |
|||
Questo gruppo ha il vettore <math>\begin{bmatrix}1 \\ 0\end{bmatrix}</math> fissato da questo omomorfismo, ma il sottospazio complementare manda |
|||
:<math>\begin{bmatrix} 0 \\ 1 \end{bmatrix} \mapsto \begin{bmatrix} a \\ 1 \end{bmatrix}</math> |
|||
dando solo una sottorappresentazione irriducibile. Questo è vero per tutti i gruppi unipotenti<ref>{{Cita libro|autore=Humphreys, James E.|titolo=Linear Algebraic Groups|url=https://www.worldcat.org/oclc/853255426|data=1975|editore=Springer New York|città=New York, NY|OCLC=853255426|ISBN=978-1-4684-9443-3}}</ref><sup>, pag. 112</sup>. |
|||
=== Somme dirette e rappresentazioni indecomponibili === |
|||
Se <math>(V,\varphi)</math> e <math>(W,\psi)</math> sono rappresentazioni di un gruppo <math>G,</math> allora la [[somma diretta]] di <math>V</math> e <math>W</math> è una rappresentazione, in modo canonico, tramite l'identificazione |
|||
:<math> g\cdot (v,w) = (g\cdot v, g\cdot w).</math> |
|||
La somma diretta di due rappresentazioni non dà maggiori informazioni sul gruppo <math>G</math> rispetto a quelle che le due rappresentazioni danno individualmente. Se una rappresentazione è la somma diretta di due sottorappresentazioni proprie non banali, si dice ''decomponibile''. Altrimenti, si dice ''indecomponibile''. |
|||
=== Riducibilità completa === |
|||
In circostanze favorevoli, ogni rappresentazione di dimensione finita è una somma diretta di rappresentazioni irriducibili: tali rappresentazioni si dicono '''semisemplici'''. In questo caso, è sufficiente studiare solo le rappresentazioni irriducibili. Esempi in cui si verifica questo fenomeno di "riducibilità completa" includono i gruppi finiti (vedere il [[teorema di Maschke]]), i gruppi compatti e le algebre di Lie semisemplici. |
|||
Nei casi in cui la riducibilità completa non vale, si deve capire come le rappresentazioni indecomponibili possono essere costruite da rappresentazioni irriducibili come estensioni di un quoziente con una sottorappresentazione. |
|||
=== Prodotti tensoriali di rappresentazioni === |
|||
Supponiamo che <math>\phi_1\colon G\rightarrow \mathrm{GL}(V_1)</math> e <math>\phi_2\colon G\rightarrow \mathrm{GL}(V_2)</math> siano rappresentazioni di un gruppo <math>G.</math> Allora possiamo formare una rappresentazione <math>\phi_1\otimes\phi_2</math> di <math>G</math> che agisce sullo spazio vettoriale del [[prodotto tensoriale]] <math>V_1\otimes V_2</math> nel seguente modo: |
|||
:<math>(\phi_1\otimes\phi_2)(g)=\phi_1(g)\otimes\phi_2(g).</math> |
|||
Se <math>\phi_1</math> e <math>\phi_2</math> sono rappresentazioni di un'algebra di Lie, la formula corretta da usare è |
|||
:<math>(\phi_1\otimes\phi_2)(X)=\phi_1(X)\otimes I+I\otimes\phi_2(X).</math> |
|||
Questo prodotto può essere riconosciuto come un [[coprodotto]] su una [[coalgebra]]. In generale, il prodotto tensoriale di rappresentazioni irriducibili non è irriducibile. Il processo di decomposizione di un prodotto tensoriale come somma diretta di rappresentazioni irriducibili è noto come [[Coefficienti di Clebsch-Gordan|teoria di Clebsch-Gordan]]. |
|||
Nel caso della teoria delle rappresentazioni del gruppo <math>\mathrm{SU}(2)</math> (o equivalentemente, della sua algebra di Lie complessificata <math>\mathfrak{sl}(2;\mathbb{C})</math>), la decomposizione è facile da determinare. Le rappresentazioni irriducibili sono parametrizzate da un parametro <math>l</math> che è un numero intero non negativo o un numero [[semintero]]; la rappresentazione ha quindi dimensione <math>2l+1</math>. Supponiamo di prendere la rappresentazione prodotto tensoriale di due rappresentazioni, associate a <math>l_1</math> e <math>l_2,</math> dove assumiamo <math>l_1\geq l_2</math>. Allora il prodotto tensoriale si decompone come somma diretta di una copia di ciascuna rappresentazione associata a <math>l,</math> dove <math>l</math> va da <math>l_1-l_2</math> a <math>l_1+l_2</math> con incrementi di 1. Se, ad esempio, <math>l_1=l_2=1</math>, i valori di <math>l</math> che si considerano sono 0, 1 e 2. Quindi, la rappresentazione prodotto tensoriale di dimensione <math>3\times 3=9</math> si decompone come somma diretta di una rappresentazione unidimensionale <math>(l=0),</math> una rappresentazione tridimensionale <math>(l=1),</math> e una rappresentazione a 5 dimensioni <math>(l=2)</math>. |
|||
== Voci correlate == |
|||
*[[Rappresentazione dei gruppi]] |
|||
*[[Rappresentazioni dei gruppi di Lie]] |
|||
== Note == |
|||
<references/> |
|||
== Bibliografia == |
|||
* {{Cita libro|nome=J. L. |cognome=Alperin|titolo= Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups|isbn=978-0-521-44926-7|anno=1986}} |
|||
* {{Cita libro|nome=Armand |cognome=Borel|titolo=Essays in the History of Lie Groups and Algebraic Groups|isbn=978-0-8218-0288-5|anno=2001}} |
|||
* {{Cita libro|url=https://archive.org/details/representationth11curt|isbn=978-0-470-18975-7|anno=1962}} |
|||
* {{Cita libro|nome=Stephen |cognome=Gelbart|titolo=An Elementary Introduction to the Langlands Program|vol=10|doi=10.1090/S0273-0979-1984-15237-6|anno=1984}} |
|||
* {{Cita libro|nome=Brian|cognome=Hall|titolo=Lie Groups, Lie Algebras, and Representations: An Elementary Introduction|serie=Graduate Texts in Mathematics|edizione=2nd|vol=222|isbn=978-3319134666|anno=2015}} |
|||
* {{Cita libro|nome=James E.|cognome=Humphreys|titolo= Introduction to Lie Algebras and Representation Theory|url=https://archive.org/details/introductiontoli00jame|isbn=978-0-387-90053-7|anno=1972a}} |
|||
* {{Cita libro|nome=James E.|cognome=Humphreys|titolo=Linear Algebraic Groups|serie=Graduate Texts in Mathematics|vol=21|isbn=978-0-387-90108-4|mr=0396773|anno=1972b}} |
|||
* {{Cita pubblicazione|nome=Victor |cognome=Kac|titolo=Lie superalgebras|vol=26|doi=10.1016/0001-8708(77)90017-2|anno=1977}} |
|||
* {{Cita libro|nome=Victor |cognome=Kac|titolo=Infinite Dimensional Lie Algebras|edizione=3rd|isbn=978-0-521-46693-6|anno=1990}} |
|||
* {{Cita libro|nome=Anthony |cognome=Knapp|titolo= Representation Theory of Semisimple Groups: An Overview Based on Examples|isbn=978-0-691-09089-4|anno=2001}} |
|||
* {{Cita libro|nome1=Alexei |cognome1=Kostrikin|nome2=Yuri|cognome2=Manin|titolo=Linear Algebra and Geometry|isbn=978-90-5699-049-7|anno=1997}} |
|||
* Yurii I. Lyubich. ''Introduction to the Theory of Banach Representations of Groups''. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988. |
|||
* {{Cita libro|nome1=David |cognome1=Mumford|nome2=J.|cognome2=Fogarty|nome3=F.|cognome3=Kirwan|titolo=Geometric invariant theory|serie=Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)]|edizione=3rd|vol=34|isbn=978-3-540-56963-3|mr=0214602 <!--(1st ed. 1965)-->|anno=1994}}; {{MathSciNet|0719371}} (2nd ed.); {{MathSciNet|1304906}}(3rd ed.) |
|||
* {{Cita libro|nome=Peter J. |cognome=Olver|titolo=Classical invariant theory|isbn=978-0-521-55821-1|anno=1999}} |
|||
* {{Cita pubblicazione|url=http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0097&DMDID=DMDLOG_0039&L=1|vol=97|doi=10.1007/BF01447892|anno=1927}} |
|||
* {{Cita pubblicazione|nome=Lev |cognome=Pontryagin|titolo=The theory of topological commutative groups|vol=35|doi=10.2307/1968438|jstor=1968438|anno=1934}} |
|||
* {{Cita libro|nome=Jean-Pierre |cognome=Serre|titolo=Linear Representations of Finite Groups|url=https://archive.org/details/linearrepresenta1977serr|isbn=978-0387901909|anno=1977}} |
|||
* {{Cita libro|nome=Shlomo |cognome=Sternberg|titolo=Group Theory and Physics|url=https://archive.org/details/grouptheoryphysi0000ster|isbn=978-0-521-55885-3|anno=1994}} |
|||
* {{Cita libro|cognome=Tung|nome=Wu-Ki|titolo=Group Theory in Physics|ed=1st|anno=1985|editore=[[World Scientific Publishing|World Scientific]]|città=New Jersey·London·Singapore·Hong Kong|ISBN=978-9971966577}} |
|||
* {{Cita libro|nome=Hermann|cognome=Weyl|titolo=Gruppentheorie und Quantenmechanik|edizione=The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931|isbn=978-0-486-60269-1|anno=1928}} |
|||
* {{Cita libro|nome=Hermann|cognome=Weyl|titolo=The Classical Groups: Their Invariants and Representations|edizione=2nd|isbn=978-0-691-05756-9|anno=1946}} |
|||
* {{Cita pubblicazione|nome=Eugene |cognome=Wigner|titolo=On unitary representations of the inhomogeneous Lorentz group|vol=40|doi=10.2307/1968551|jstor=1968551|anno=1939}} |
|||
== Link esterni == |
|||
* {{SpringerEOM|titolo=Representation theory}} |
|||
* Alexander Kirillov Jr., [http://www.math.sunysb.edu/~kirillov/liegroups/ Un'introduzione ai gruppi di Lie e alle algebre di Lie] (2008). Libro di testo, versione preliminare pdf scaricabile dalla home page dell'autore. |
|||
* Kevin Hartnett, [https://www.quantamagazine.org/the-useless-perspective-that-transformed-mathematics-20200609/ (2020), articolo sulla teoria della rappresentazione nella rivista Quanta]. |
|||
{{Portale|matematica}} |
|||
[[Categoria:Teoria delle rappresentazioni]] |
|||
Versione delle 13:03, 26 set 2021
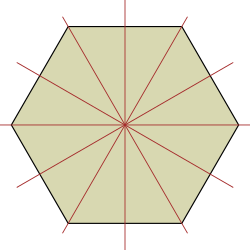
La teoria delle rappresentazioni è una branca della matematica che studia le strutture algebriche astratte "rappresentando" i loro elementi come trasformazioni lineari di spazi vettoriali[1] e studiando i moduli su queste strutture algebriche astratte.[2] Sostanzialmente una rappresentazione rende più concreto un oggetto algebrico astratto descrivendo i suoi elementi mediante matrici. La teoria delle matrici e delle trasformazioni lineari è ben nota, quindi rappresentazioni di oggetti più astratti in termini di oggetti familiari dell'algebra lineare semplifica i calcoli e aiuta a capire e determinare le proprietà di questi oggetti astratti.
Un gruppo di Lie è un gruppo che è anche una varietà differenziabile. Molti gruppi classici di matrici sui numeri reali o complessi sono gruppi di Lie. Molti gruppi importanti in fisica e chimica sono gruppi di Lie e la loro teoria delle rappresentazioni è cruciale per l'applicazione della teoria dei gruppi in questi campi.
La teoria delle rappresentazioni è uno strumento utile in quanto riduce problemi di algebra astratta a problemi di algebra lineare. Inoltre lo spazio vettoriale su cui (per esempio) un gruppo è rappresentato può essere di dimensione infinita. Se questo, per esempio, è uno spazio di Hilbert, allora i metodi dell'analisi funzionale possono essere applicati alla teoria dei gruppi.[3][4] La teoria delle rappresentazioni è importante anche in fisica poiché, per esempio, descrive come il gruppo di simmetria di un sistema fisico influenza le soluzioni delle equazioni che descrivono il sistema.[5]
La teoria delle rappresentazioni è presente in tutti i campi della matematica per due ragioni. In primo luogo, le applicazioni della teoria delle rappresentazioni sono diverse; oltre al suo impatto sull'algebra, la teoria delle rappresentazioni:
- rende più chiara e generalizza l'analisi di Fourier tramite l'analisi armonica;
- è connessa alla geometria tramite la teoria degli invarianti e il programma di Erlangen;
- ha un impatto sulla teoria dei numeri tramite le forme automorfe e il programma Langlands.
In secondo luogo, ci sono diversi approcci alla teoria delle rappresentazioni. Gli stessi oggetti possono essere studiati usando metodi della geometria algebrica, della teoria dei moduli, della teoria analitica dei numeri, della geometria differenziale, della teoria degli operatori, della combinatoria algebrica e della topologia.
Il successo della teoria delle rappresentazioni ha portato a numerose generalizzazioni. Una delle versioni più generali si ha nella teoria delle categorie. Gli oggetti algebrici a cui si applica la teoria delle rappresentazioni possono essere visti come particolari tipi di categorie e le rappresentazioni come funtori dalla categoria degli oggetti algebrici considerati alla categoria degli spazi vettoriali.[6] Questa descrizione indica due ovvie generalizzazioni: primo, gli oggetti algebrici possono essere sostituiti da categorie più generali; secondo, la categoria di arrivo degli spazi vettoriali può essere sostituita da altre categorie ben studiate.
Definizioni e concetti
Sia uno spazio vettoriale su un campo . Per esempio supponiamo che sia o lo spazio vettoriale -dimensionale standard sui reali o sui complessi, rispettivamente. In questo caso, l'idea della teoria delle rappresentazioni è lavorare con l'algebra astratta in concreto usando le matrici di numeri reali o complessi.
Ci sono tre tipi principali di oggetti algebrici su cui può essere fatto: gruppi, algebre associative e algebre di Lie.[6]
- L'insieme di tutte le matrici invertibili di ordine è un gruppo rispetto alla moltiplicazione di matrici e la teoria delle rappresentazioni dei gruppi analizza un gruppo descrivendo ("rappresentando") i suoi elementi in termini di matrici invertibili.
- L'addizione e la moltiplicazione di matrici rendono l'insieme di tutte le matrici un'algebra associativa, e quindi esiste una corrispondente teoria delle rappresentazioni delle algebre associative.
- Se sostituiamo la moltiplicazione di matrici con il commutatore di matrici l'insieme delle matrici di ordine diventa invece un'algebra di Lie, portando a una teoria delle rappresentazioni delle algebre di Lie.
Questo si generalizza a qualsiasi campo e qualsiasi spazio vettoriale su sostituendo le matrici con le funzioni lineari e la moltiplicazione di matrici con la composizione; cioè, per ogni spazio vettoriale su esiste un gruppo GL(V,F) di automorfismi di essite un'algebra associativa di tutti endomorfismi di e una corrispondente algebra di Lie
Definizione
Ci sono due modi per definire una rappresentazione. Il primo utilizza l'idea di azione di gruppo, generalizzando il modo in cui le matrici agiscono sui vettori colonna mediante la moltiplicazione matriciale. Una rappresentazione di un gruppo o di un'algebra (associativa o di Lie) su uno spazio vettoriale è una funzione
con due proprietà. Primo, per ogni (o ), la funzione
è lineare (su ). Secondo, se introduciamo la notazione per per ogni e :
dove è l'elemento neutro di e è il prodotto in Il requisito per le algebre associative è analogo, tranne per il fatto che le algebre associative non hanno sempre un elemento neutro, nel qual caso l'equazione (1) viene ignorata. L'equazione (2) è un'espressione astratta dell'associatività della moltiplicazione di matrici. Questo non vale per il commutatore di matrici e inoltre non vi è alcun elemento neutro per il commutatore. Quindi per le algebre di Lie, l'unico requisito è che per ogni e :
dove è la parentesi di Lie, che generalizza il commutatore di matrici
Il secondo modo per definire una rappresentazione è tramite la funzione che manda in una funzione lineare che soddisfa
e analogamente negli altri casi. Questo approccio è più conciso e più astratto. Da questo punto di vista:
- una rappresentazione di un gruppo su uno spazio vettoriale è un omomorfismo di gruppi ;[7]
- una rappresentazione di un'algebra associativa su uno spazio vettoriale è un omomorfismo di algebre ;
- una rappresentazione di un'algebra di Lie su uno spazio vettoriale è un omomorfismo di algebre di Lie .
Terminologia
Lo spazio vettoriale è chiamato spazio di rappresentazione di e la sua dimensione (se finita) è chiamata dimensione della rappresentazione (a volte grado, come in [8]). È anche pratica comune riferirsi a stesso come alla rappresentazione quando l'omomorfismo è chiaro dal contesto; altrimenti la notazione può essere usata per indicare una rappresentazione.
Quando è di dimensione finita si può scegliere una base per per identificare con e quindi recuperare una rappresentazione matriciale con elementi nel campo
Una rappresentazione effettiva o fedele è una rappresentazione per la quale l'omomorfismo è iniettivo.
Funzioni equivarianti e isomorfismi
Se e sono spazi vettoriali su con rappresentazioni e di un gruppo allora una funzione equivariante da a è una funzione lineare tale che
per ogni e In termini di e questo significa
per ogni cioè, il diagramma seguente commuta:
Le funzioni equivarianti per le rappresentazioni di un'algebra associativa o di Lie sono definite in modo simile. Se è invertibile, allora si dice che è un isomorfismo, nel qual caso e (o, più precisamente, e ) sono rappresentazioni isomorfe, anche dette rappresentazioni equivalenti. Una funzione equivariante è spesso chiamata funzione intrecciata delle rappresentazioni. Inoltre, nel caso di un gruppo a volte è chiamato -funzione.
Le rappresentazioni isomorfe sono, per scopi pratici, "le stesse"; forniscono le stesse informazioni sul gruppo o sull'algebra rappresentati. La teoria delle rappresentazioni cerca quindi di classificare le rappresentazioni a meno di isomorfismo.
Sottorappresentazioni, quozienti e rappresentazioni irriducibili
Se è una rappresentazione di un gruppo e è un sottospazio vettoriale di che è preservato dall'azione di ossia per ogni e si ha (Serre chiama stabile rispetto a ), quindi è chiamata sottorappresentazione. Definendo
dove è la restrizione di per allora è una rappresentazione di e l'inclusione di è una funzione equivariante. Anche lo spazio quoziente ha una struttura di rappresentazione di . Se ha esattamente due sottorappresentazioni, vale a dire il sottospazio banale e stessa, allora la rappresentazione è detta irriducibile. Se ha una sottorappresentazione non banale propria, si dice che la rappresentazione è riducibile.[9] La definizione di rappresentazione irriducibile implica il lemma di Schur: una funzione equivariante
tra rappresentazioni irriducibili o è la funzione zero o è un isomorfismo, poiché il nucleo e l'immagine sono sottorappresentazioni. In particolare, quando questo mostra che gli endomorfismi equivarianti di formano un'algebra di divisione associativa sul campo sottostante Se è algebricamente chiuso, gli unici endomorfismi equivarianti di una rappresentazione irriducibile sono i multipli scalari dell'identità. Le rappresentazioni irriducibili sono gli elementi costitutivi della teoria delle rappresentazioni per molti gruppi: se una rappresentazione non è irriducibile, allora è costruita apartire da una sottorappresentazione e da un quoziente entrambi, in un certo senso, "più semplici". Per esempio, se è di dimensione finita, allora sia la sottorappresentazione che il quoziente hanno dimensione minore. Ci sono controesempi in cui una rappresentazione ha una sottorappresentazione, ma ha solo una componente irriducibile non banale. Ad esempio, il gruppo additivo ha una rappresentazione bidimensionale
Questo gruppo ha il vettore fissato da questo omomorfismo, ma il sottospazio complementare manda
dando solo una sottorappresentazione irriducibile. Questo è vero per tutti i gruppi unipotenti[10], pag. 112.
Somme dirette e rappresentazioni indecomponibili
Se e sono rappresentazioni di un gruppo allora la somma diretta di e è una rappresentazione, in modo canonico, tramite l'identificazione
La somma diretta di due rappresentazioni non dà maggiori informazioni sul gruppo rispetto a quelle che le due rappresentazioni danno individualmente. Se una rappresentazione è la somma diretta di due sottorappresentazioni proprie non banali, si dice decomponibile. Altrimenti, si dice indecomponibile.
Riducibilità completa
In circostanze favorevoli, ogni rappresentazione di dimensione finita è una somma diretta di rappresentazioni irriducibili: tali rappresentazioni si dicono semisemplici. In questo caso, è sufficiente studiare solo le rappresentazioni irriducibili. Esempi in cui si verifica questo fenomeno di "riducibilità completa" includono i gruppi finiti (vedere il teorema di Maschke), i gruppi compatti e le algebre di Lie semisemplici.
Nei casi in cui la riducibilità completa non vale, si deve capire come le rappresentazioni indecomponibili possono essere costruite da rappresentazioni irriducibili come estensioni di un quoziente con una sottorappresentazione.
Prodotti tensoriali di rappresentazioni
Supponiamo che e siano rappresentazioni di un gruppo Allora possiamo formare una rappresentazione di che agisce sullo spazio vettoriale del prodotto tensoriale nel seguente modo:
Se e sono rappresentazioni di un'algebra di Lie, la formula corretta da usare è
Questo prodotto può essere riconosciuto come un coprodotto su una coalgebra. In generale, il prodotto tensoriale di rappresentazioni irriducibili non è irriducibile. Il processo di decomposizione di un prodotto tensoriale come somma diretta di rappresentazioni irriducibili è noto come teoria di Clebsch-Gordan.
Nel caso della teoria delle rappresentazioni del gruppo (o equivalentemente, della sua algebra di Lie complessificata ), la decomposizione è facile da determinare. Le rappresentazioni irriducibili sono parametrizzate da un parametro che è un numero intero non negativo o un numero semintero; la rappresentazione ha quindi dimensione . Supponiamo di prendere la rappresentazione prodotto tensoriale di due rappresentazioni, associate a e dove assumiamo . Allora il prodotto tensoriale si decompone come somma diretta di una copia di ciascuna rappresentazione associata a dove va da a con incrementi di 1. Se, ad esempio, , i valori di che si considerano sono 0, 1 e 2. Quindi, la rappresentazione prodotto tensoriale di dimensione si decompone come somma diretta di una rappresentazione unidimensionale una rappresentazione tridimensionale e una rappresentazione a 5 dimensioni .
Voci correlate
Note
- ^ (EN) The Definitive Glossary of Higher Mathematical Jargon — Mathematical Representation, su mathvault.ca, 1º agosto 2019.
- ^ representation theory in nLab, su ncatlab.org.
- ^ Sally e Vogan.
- ^ Constantin Teleman, Representation Theory (PDF), su math.berkeley.edu, 2005.
- ^ Sternberg.
- ^ a b www-math.mit.edu, http://www-math.mit.edu/~etingof/replect.pdf. URL consultato il 9 dicembre 2019.
- ^ math.berkeley.edu, https://math.berkeley.edu/~teleman/math/RepThry.pdf. URL consultato il 9 dicembre 2019.
- ^ Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Springer-Verlag, ISBN 978-0387901909
- ^ La rappresentazione {0} di dimensione zero è considerata non essere riducibile né irriducibile, analogamente al numero 1 che non è considerato compost né primo.
- ^ Humphreys, James E., Linear Algebraic Groups, New York, NY, Springer New York, 1975, ISBN 978-1-4684-9443-3, OCLC 853255426.
Bibliografia
- J. L. Alperin, Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups, 1986, ISBN 978-0-521-44926-7.
- Armand Borel, Essays in the History of Lie Groups and Algebraic Groups, 2001, ISBN 978-0-8218-0288-5.
- 1962, ISBN 978-0-470-18975-7, https://archive.org/details/representationth11curt.
- Stephen Gelbart, An Elementary Introduction to the Langlands Program, vol. 10, 1984, DOI:10.1090/S0273-0979-1984-15237-6.
- Brian Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222, 2nd, 2015, ISBN 978-3319134666.
- James E. Humphreys, Introduction to Lie Algebras and Representation Theory, 1972a, ISBN 978-0-387-90053-7.
- James E. Humphreys, Linear Algebraic Groups, Graduate Texts in Mathematics, vol. 21, 1972b, ISBN 978-0-387-90108-4, MR 0396773.
- Victor Kac, Lie superalgebras, vol. 26, 1977, DOI:10.1016/0001-8708(77)90017-2.
- Victor Kac, Infinite Dimensional Lie Algebras, 3rd, 1990, ISBN 978-0-521-46693-6.
- Anthony Knapp, Representation Theory of Semisimple Groups: An Overview Based on Examples, 2001, ISBN 978-0-691-09089-4.
- Alexei Kostrikin e Yuri Manin, Linear Algebra and Geometry, 1997, ISBN 978-90-5699-049-7.
- Yurii I. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
- David Mumford, J. Fogarty e F. Kirwan, Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34, 3rd, 1994, ISBN 978-3-540-56963-3, MR 0214602.; MR 0719371 (2nd ed.); MR 1304906(3rd ed.)
- Peter J. Olver, Classical invariant theory, 1999, ISBN 978-0-521-55821-1.
- vol. 97, 1927, DOI:10.1007/BF01447892, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0097&DMDID=DMDLOG_0039&L=1.
- Lev Pontryagin, The theory of topological commutative groups, vol. 35, 1934, DOI:10.2307/1968438, JSTOR 1968438.
- Jean-Pierre Serre, Linear Representations of Finite Groups, 1977, ISBN 978-0387901909.
- Shlomo Sternberg, Group Theory and Physics, 1994, ISBN 978-0-521-55885-3.
- Wu-Ki Tung, Group Theory in Physics, 1stª ed., New Jersey·London·Singapore·Hong Kong, World Scientific, 1985, ISBN 978-9971966577.
- Hermann Weyl, Gruppentheorie und Quantenmechanik, The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931, 1928, ISBN 978-0-486-60269-1.
- Hermann Weyl, The Classical Groups: Their Invariants and Representations, 2nd, 1946, ISBN 978-0-691-05756-9.
- Eugene Wigner, On unitary representations of the inhomogeneous Lorentz group, vol. 40, 1939, DOI:10.2307/1968551, JSTOR 1968551.
Link esterni
- (EN) Representation theory, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
- Alexander Kirillov Jr., Un'introduzione ai gruppi di Lie e alle algebre di Lie (2008). Libro di testo, versione preliminare pdf scaricabile dalla home page dell'autore.
- Kevin Hartnett, (2020), articolo sulla teoria della rappresentazione nella rivista Quanta.




























![{\displaystyle (2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afaecb499ef33395596d8b25191fc31577801b06)
![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)