Vai al contenuto

Statistica

Modifica collegamenti
Da Wikipedia, l'enciclopedia libera.
(Reindirizzamento da Analisi statistica)
Copertina di un libro sulla statistica del 1872 ("La Statistica e i suoi metodi, suo ufficio scientifico e competenza di applicazione").

La statistica è una scienza che ha come scopo lo studio quantitativo e qualitativo di un particolare fenomeno collettivo in condizioni di incertezza o non determinismo, cioè di non completa conoscenza di esso o di una sua parte.

Strumento del metodo scientifico,[1] si avvale della matematica per studiare i modi in cui un fenomeno collettivo può essere sintetizzato e compreso e ciò avviene attraverso la raccolta e l'analisi delle informazioni relative al fenomeno studiato;[2] con il termine statistica, nel linguaggio di tutti i giorni, si indicano anche semplicemente i risultati numerici (le statistiche richiamate nei telegiornali, ad es. l'inflazione, il PIL, ecc.) di un processo di sintesi dei dati osservati, cioè gli indici statistici.

Storia

[modifica | modifica wikitesto]
Lo stesso argomento in dettaglio: Storia della statistica.

Per molti etimologicamente legata a status (inteso come stato politico, così come stato delle cose: status rerum), la misura quantitativa dei fenomeni sociali ha una storia antica;[3] in Egitto si rilevava l'ammontare della popolazione già ai tempi della prima dinastia e durante la seconda si rilevavano vari beni a fini fiscali; durante le dinastie successive si tenevano elenchi delle famiglie dei soldati, dei dipendenti statali e delle merci; sotto la XX dinastia si tenevano liste delle abitazioni e dei loro abitanti.

Stando alla Bibbia, in Israele il primo censimento fu fatto ai tempi del soggiorno nel Sinai (da cui il libro dei Numeri della Bibbia) e altri ne seguirono. Anche l'immenso impero cinese ha sempre curato i censimenti, che nell'epoca dei Ming avevano cadenza decennale. Non si hanno invece notizie di censimenti nella Grecia antica, ma venivano registrati ogni anno i nati dell'anno precedente. La rilevazione dei cittadini e dei loro beni ebbe grande importanza nella Roma antica. Il primo censimento fu ordinato da Servio Tullio e si ebbero poi censimenti con periodicità quinquennale dalla fine del VI secolo a.C., decennale a partire da Augusto.

La caduta dell'Impero romano d'Occidente comportò la sospensione di tali attività per secoli, fino alla ricostituzione di organismi statali da parte dei Carolingi. Il sorgere dei Comuni, poi delle signorie, delle repubbliche marinare e degli Stati nazionali comportò una progressiva frammentazione non solo politica, ma anche amministrativa. Già dal XII secolo si ebbero rilevazioni statistiche in Italia, da Venezia alla Sicilia, con obiettivi prevalentemente fiscali. Ebbero poi crescente importanza le registrazioni su nascite, matrimoni e morti effettuate dalle parrocchie, iniziate in Italia ed in Francia fin dal XIV secolo.

L'esigenza di quantificare i fenomeni oggetto di studio, ossia di analizzarli e descriverli in termini matematici, fu una tendenza tipica del XVII secolo: non fu solo l'Universo ad essere concepito come un grande libro "scritto in caratteri matematici", come aveva affermato Galileo Galilei, ma si diffuse anche la convinzione che fosse possibile studiare la società tramite strumenti di tipo quantitativo.

In genere, le origini della statistica nella concezione più moderna, si fanno risalire a quella che un economista e matematico inglese, William Petty (1623-1687), chiamò "aritmetica politica", ovvero "l'arte di ragionare mediante le cifre sulle cose che riguardano il governo"; tra le cose che maggiormente interessavano al governo, del resto, vi erano l'entità della popolazione e la quantità di ricchezza che essa aveva a sua disposizione, dalle quali dipendeva in ultima analisi la forza degli Stati in competizione tra loro. Demografia e calcolo del reddito nazionale furono quindi gli ambiti in cui si esercitò la creatività dei primi "aritmeti politici".

Nel primo campo un autentico precursore fu John Graunt (1620-1674), un mercante londinese, che tramite lo studio dei registri di mortalità, riuscì per primo a rilevare l'approssimativa costanza di certi rapporti demografici e a costruire una prima e rudimentale "tavola della mortalità". Le sue Natural and Political Observations on the Bills of Mortality risalenti al 1662 possono essere considerate a buon diritto come l'opera fondatrice della demografia. Il metodo statistico elaborato da Graunt per il settore demografico fu poi ripreso da William Petty, che nel suo Political Arithmetic, pubblicato postumo nel 1690, espose i principi fondamentali della nuova disciplina.

Nei medesimi anni, venne data alle stampe l'opera di un altro grande aritmeta politico, Gregory King (1648-1712), il quale nelle sue Natural and Political Observations and Conclusion upon the State and Condition of England, risalenti al 1698, formulò una stima della popolazione e del reddito totale dell'Inghilterra, giungendo a conclusioni ritenute abbastanza verosimili. In Francia un tentativo simile venne effettuato dal ministro del re Luigi XIV ed economista Sébastien de Vauban (1633-1707), che stimò la popolazione del Regno di Francia intorno ai venti milioni di abitanti - valutazione condivisa dagli storici attuali.

Ai problemi statistici si interessarono anche alcune delle menti più brillanti dell'epoca: il fisico olandese Christiaan Huygens (1629-1695) elaborò delle tavole di mortalità, l'astronomo inglese Edmund Halley (1656-1742) avanzò una serie di ipotesi sul numero di abitanti dei vari Paesi europei, mentre in Germania il grande filosofo Gottfried Leibniz (1646-1716) suggerì la creazione di un ufficio statale di statistica. Degna di nota, in Italia, è anche l'opera di Luca de Samuele Cagnazzi (1764-1852), il quale per primo, in Italia, fornì una definizione di statistica, nonché dei suoi scopi e limiti, in un periodo in cui, con Melchiorre Gioia, la disciplina viaggiava ancora nell'indeterminato.[4][5]

Nel frattempo, in concomitanza con lo sviluppo di queste prime ed ancora rudimentali metodologie demografiche, ci si cominciò a porre questo tipo di problemi anche per quanto concerneva la storia precedente: ciò indusse a guardare in modo critico e diffidente ai dati forniti da quegli autori del passato che avevano cercato di quantificare il numero di abitanti di un territorio, le dimensioni di un esercito, i morti per un'epidemia, ecc. Un contributo importante, sotto questo profilo, venne da uno dei più grandi pensatori del XVIII secolo, lo scozzese David Hume (1711-1776) il cui Of the Populousness of Ancient Nations diede inizio alla cosiddetta "demografia storica". In tale testo Hume rilevò come le cifre tramandateci dagli antichi fossero particolarmente inaffidabili, non solo perché le loro stime non avevano basi solide, ma anche perché i numeri di ogni tipo contenuti negli antichi manoscritti sono stati soggetti ad un'alterazione molto maggiore di qualsiasi altra parte del testo, in quanto ogni altro tipo di alterazione modifica il senso e la grammatica, ed è quindi più facilmente individuata dal lettore e dal trascrittore.

Nel XVIII secolo fu definita e proposta dal filosofo tedesco Gottfried Achenwall come scienza deputata a raccogliere dati utili per governare meglio.

Descrizione

[modifica | modifica wikitesto]

La scienza statistica è comunemente suddivisa in due branche principali:

Statistica descrittiva

[modifica | modifica wikitesto]
Esempio di grafico statistico per la rappresentazione dei dati raccolti: popolazione per età e sesso a Mogliano Veneto (2007).

La statistica descrittiva ha come scopo quello di sintetizzare i dati attraverso i suoi strumenti grafici (diagrammi a barre, a torta, istogrammi, box-plot) e indici (indicatori statistici, indicatori di posizione come la media, di dispersione, come la varianza e la concentrazione, di correlazione, di forma, come la curtosi e l'asimmetria, ecc.) che descrivono gli aspetti salienti dei dati osservati, formando così il contenuto statistico.

Statistica inferenziale

[modifica | modifica wikitesto]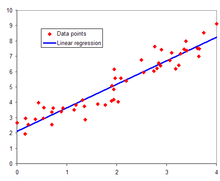
Esempio di inferenza (regressione lineare) dedotta a partire da un insieme di dati.

La statistica inferenziale ha come obiettivo, invece, quello di stabilire delle caratteristiche dei dati e dei comportamenti delle misure rilevate (variabili statistiche) con una possibilità di errore predeterminata. Le inferenze possono riguardare la natura teorica (la legge probabilistica) del fenomeno che si osserva.

La conoscenza di questa natura permetterà poi di fare una previsione (si pensi, ad esempio, che quando si dice che "l'inflazione il prossimo anno avrà una certa entità" deriva dal fatto che esiste un modello dell'andamento dell'inflazione derivato da tecniche inferenziali). La statistica inferenziale è fortemente legata alla teoria della probabilità.

Sotto questo punto di vista descrivere in termini probabilistici o statistici un fenomeno aleatorio nel tempo, caratterizzabile dunque da una variabile aleatoria, vuol dire descriverlo in termini di distribuzione di probabilità e dei suoi parametri, come media e varianza. La statistica inferenziale si suddivide poi in altri capitoli, di cui i più importanti sono la teoria della stima (stima puntuale e stima intervallare) e la verifica delle ipotesi.

Applicazioni

[modifica | modifica wikitesto]

La statistica è utile ovunque sia necessaria una delle seguenti condizioni:

  • procedere ad una raccolta ordinata, ad una stesura comprensibile e ad una elaborazione dei dati più svariati;
  • scoprire eventuali leggi che regolano i dati spesso solo in apparenza disordinati ed operarne il confronto;
  • definire una variabile di riferimento che assuma diversi valori definibili in un certo intervallo di variazione.

Il metodo e le tecniche statistiche, tipicamente teoriche, assumono importanza fondamentale in molti altri ambiti applicativi di studio quale ad esempio la fisica (fisica statistica) qualora per manifesta complessità di analisi si debba rinunciare ad avere informazioni di tipo deterministico su sistemi fisici complessi o a molti gradi di libertà accettandone invece una sua descrizione statistica. Tra queste discipline ci sono anche l'economia, che si appoggia fortemente alla statistica (statistica economica, statistica aziendale ed econometria, oltre alla teoria dei giochi e delle decisioni) nella descrizione qualitativa (serie storiche) e quantitativa (modelli statistici) dei fenomeni socio-economici che incorrono all'interno del sistema economico; e alla psicologia, che si appoggia alla statistica nella ricerca delle caratteristiche e degli atteggiamenti degli individui e le loro differenze (psicometria). La statistica è uno strumento essenziale nella ricerca medica. La biostatistica fornisce infatti gli strumenti per tradurre l'esperienza clinica e di laboratorio in espressioni quantitative, tese a individuare se, e in che misura, un trattamento o una procedura abbia avuto effetto su un gruppo di pazienti.[6] Un'altra applicazione estremamente comune nella società è quella dei sondaggi d'opinione, analisi di mercato e in generale qualunque analisi di dati campionari.

Nell'ambito dell'epistemologia post-positivista si sono sollevate voci critiche sull'attendibilità della statistica rispetto ai fenomeni non commensurabili e rispetto al concetto di inferenza statistica. Da un lato autori come il matematico Giorgio Israel criticano in radice la dignità epistemologica della statistica laddove non si limiti a descrivere gli andamenti delle popolazioni e laddove pretenda di occuparsi di fenomeni essenzialmente qualitativi come il comportamento individuale, la psicologia e persino i fenomeni biologici complessi.[7] Dall'altro autori come l'ingegnere e matematico Bruno de Finetti hanno messo in evidenza la natura essenzialmente soggettiva, e non più attendibile di una gradazione di fiducia, di ogni valutazione di probabilità, e di conseguenza di ogni induzione e inferenza che parta dal campione per "asserire" connotati di una popolazione.[8]

Note

[modifica | modifica wikitesto]
  1. ^ Pere Grima, La certezza assoluta e altre finzioni. I segreti della statistica. RBA Italia (Mondo matematico 13); 2011.
  2. ^ Glossario Istat, su www3.istat.it (archiviato dall'url originale il 31 dicembre 2011).
  3. ^ Le informazioni che seguono sono tratte dal Leti.
  4. ^ Gabaglio, pp. 88-100.
  5. ^ Lamiavita, pp. 72-73 e 313, nota 144.
  6. ^ Stanton A. Glantz. Statistica per discipline biomediche. McGraw-Hill; 2007. ISBN 978-88-386-3925-8.
  7. ^ Giorgio Israel, La matematica e la realtà. Capire il mondo con i numeri, Roma, Carocci, 2015.
  8. ^ Bruno de Finetti, Definizione soggettivista o il concetto bayesiano di probabilità, su progettomatematica.dm.unibo.it.

Bibliografia

[modifica | modifica wikitesto]
  • Massimiliano Gallo, L'esame di statistica, UNI Service, Trento, 2009, ISBN 978-88-6178-338-6.
  • Pietro Boccia, Metodologia della ricerca, Simone editore, Napoli, 2018, ISBN 978-88-914-1529-5.
  • S. Borra, A. Di Ciaccio. Statistica: metodologie per le scienze economiche e sociali, Milano, McGraw-Hill, 2008, ISBN 978-88-386-6428-1.
  • M. K. Pelosi, T. M. Sandifer, P. Cerchiello, P. Giudici. "Introduzione alla Statistica", Milano, McGraw-Hill, 2008, ISBN 978-88-386-6516-5.
  • D. Piccolo. Statistica. Bologna, Il Mulino, 2000.
  • Antonio Gabaglio, Storia e teoria generale della statistica, vol. 1, Milano, 1888, pp. 88-100.
  • G. Leti (1983): Statistica descrittiva, Bologna, Il Mulino, ISBN 88-15-00278-2.
  • G. Landenna, D. Marasini, P. Ferrari. Teoria della stima. Bologna, Il Mulino, 1997.
  • G. Landenna, D. Marasini, P. Ferrari. La verifica di ipotesi statistiche. Bologna, Il Mulino, 1998.
  • G. Landenna, D. Marasini, P. Ferrari. Probabilità e variabili casuali. Bologna, Il Mulino, 1997.
  • Yuri A. Rozanov (1995): Probability Theory, Random Processes and Mathematical statistics, Kluwer, ISBN 0-7923-3764-6.
  • Mark J. Schervish (1997): Theory of Statistics, Springer, ISBN 0-387-94546-6.
  • Jun Shao (1999): Mathematical statistics, Springer, ISBN 0-387-98674-X.
  • Vijay K. Rohatgi, A. K. Md. Ehsanes Saleh (2002): An introduction to Probability and Statistics, 2nd edition, J.Wiley, ISBN 0-471-34846-5
  • Luca de Samuele Cagnazzi, La mia vita, a cura di Alessandro Cutolo, Milano, Ulrico Hoepli, 1944.
  • Alberto Rotondi, Paolo Pedroni, Antonio Pievatolo, 4ª edizione (2021): Probabilità, Statistica e Simulazione, Springer, ISBN 978-88-470-4009-0
  • A.M. Mood, F.A. Graybill, D.C. Boes (1991): Introduzione alla statistica, McGraw Hill Italia, ISBN 88-386-0661-7.
  • A. Rizzi (1992): Inferenza Statistica, Torino, UTET, ISBN 88-7750-014-X.
  • O. Vitali (1993): Statistica per le scienze applicate, Cacucci editore, ISBN 600-04-1098-0.
  • A. Mondani (1991): Corso di statistica descrittiva, LED Edizioni Universitarie, ISBN 978-88-791-6002-5.
  • A. M. Gambotto Manzone, B. Consolini: Nuovo Matematica Generale e Applicata con gli strumenti informatici - Modulo 6 - Statistica e calcolo delle probabilità, Tramontana, 2005. ISBN 88-233-0288-9.
  • M. Ross Sheldon, Introduzione alla statistica, 2ª ed., Maggioli Editore, 2014, ISBN 88-916-0267-1.

Voci correlate

[modifica | modifica wikitesto]

Altri progetti

[modifica | modifica wikitesto]

Collegamenti esterni

[modifica | modifica wikitesto]
Controllo di autoritàThesaurus BNCF 5101 · LCCN (EN) sh85127580 · GND (DE) 4056995-0 · BNF (FR) cb11938470p (data) · J9U (EN, HE) 987007531886805171 · NDL (EN, JA) 00573173
  Portale Matematica
Estratto da "https://it.wikipedia.org/w/index.php?title=Statistica&oldid=141729335"