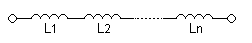Induttore
| Induttore | |
|---|---|
 | |
| Tipo | Passivo |
| Principio di funzionamento | Induzione elettromagnetica |
| Prima produzione | Michael Faraday (1831) |
| Simbolo elettrico | |

| |
| Vedi: componente elettronico | |
L'induttore è un componente elettrico che genera un campo magnetico al passaggio di corrente elettrica (continua o alternata o impulsiva).
Nella teoria dei circuiti, l'induttore è un componente ideale (la cui grandezza fisica è l'induttanza) in cui tutta l'energia elettrica assorbita è immagazzinata nel campo magnetico prodotto. Gli induttori reali, realizzati con un avvolgimento di un filo conduttore, presentano anche fenomeni dissipativi e capacitivi di cui si deve tenere conto.
Inoltre, nei circuiti in regime sinusoidale permanente, l'induttore determina una differenza di fase di 90 gradi fra la tensione applicata e la corrente che lo attraversa: in particolare, in queste condizioni di funzionamento, la corrente che attraversa un induttore ideale risulta essere sfasata in ritardo di un quarto di periodo rispetto alla tensione applicata ai suoi morsetti.
Gli induttori sono impiegati in una varietà di dispositivi elettrici ed elettronici, tra i quali i trasformatori e i motori elettrici, nonché in svariati circuiti a corrente alternata ad alta frequenza.
Fisica dell'induttore[modifica | modifica wikitesto]

Realizzazione[modifica | modifica wikitesto]
Un induttore è costituito da un avvolgimento di materiale conduttivo, generalmente filo di rame, ricoperto da una sottile pellicola isolante o un filo litz[1], in pratica, si può assumere un induttore come un solenoide. Per aumentare l'induttanza, si usa spesso realizzare l'avvolgimento su un nucleo di materiale con elevata permeabilità magnetica (ad esempio, ferriti), i quali di contro portano a perdite per le correnti parassite, con conseguente perdita del fattore qualità.[1] Un induttore può anche essere inserito in un circuito integrato. In questo caso comunemente si usa l'alluminio come materiale conduttore. È, tuttavia, raro che un induttore sia inserito in un circuito integrato: limiti pratici rendono molto più comune l'uso di un circuito chiamato "giratore", che usa un condensatore per simulare il comportamento di un induttore. Piccoli induttori usati per frequenze molto alte sono talvolta realizzati con un semplice filo che attraversa un cilindro o una perlina (piccolo anello) di ferrite.
Induttanza[modifica | modifica wikitesto]
Per capire il concetto di autoinduzione, la cui induttanza ne è il suo coefficiente, bisogna prendere in esame una spira circolare percorsa da una certa corrente I. La spira, come qualsiasi circuito conduttore percorso da corrente, secondo la legge elementare di Laplace, è sorgente di campo magnetico. La stessa spira, sorgente del campo magnetico B, risente del flusso di B concatenato al circuito. Si chiama dunque flusso magnetico autoindotto in quanto viene generato e percepito dallo stesso circuito conduttore. L’induttanza si chiama anche coefficiente di autoinduzione. L'induttore è l'elemento fisico, e la sua grandezza fisica si chiama induttanza. Naturalmente, il filo di rame ha una resistenza elettrica, particolarmente alle alte frequenze (effetto pelle), e tra le spire vicine vi è un accoppiamento capacitivo. Inoltre, vanno tenute presenti le perdite nel nucleo magnetico eventualmente introdotto. Questi ed altri fenomeni parassiti (parassiti perché non voluti) differenziano l'induttore reale dall'induttore ideale. Spesso nella pratica l'induttore viene chiamato con la sua grandezza fisica (induttanza).
Energia[modifica | modifica wikitesto]
L'energia immagazzinata nell'induttore (misurata in Joule nel SI) è uguale alla quantità di lavoro richiesta per ottenere la corrente che scorre in esso e quindi per generare il campo magnetico. Questa è data da:
dove I è la corrente che scorre nell'induttore e L l'induttanza. W invece corrisponde all'energia immagazzinata nell'induttore ed è anche espressa con questa lettera dell'alfabeto.
Circuiti elettrici[modifica | modifica wikitesto]

Un induttore si oppone solo alle variazioni di corrente. Se fosse ideale, non presenterebbe nessuna resistenza alla corrente continua, se non quando viene attivata e quando viene tolta (in questi fenomeni transitori l'induttore tende a smorzare le variazioni della corrente). Ma l'induttore reale presenta una resistenza elettrica non nulla e, quindi, il circuito in cui è inserito spende energia anche per mantenere una corrente costante che non varia il campo magnetico creato, ma si dissipa nella resistenza presentata dal filo di rame. In generale, trascurando gli eventi parassiti (resistenza e capacità), la relazione tra la tensione applicata agli estremi dell'induttore con induttanza L e la corrente i(t) che varia nel tempo e scorre nell'induttore è descritta dall'equazione differenziale:
se ne deduce che se una corrente variabile nel tempo, come ad esempio una corrente alternata sinusoidale, scorre nell'induttore, una tensione variabile nel tempo (alternata nel caso di corrente alternata) o forza elettromotrice (abbr. f.e.m.) viene indotta ai capi dell'induttore stesso. Questa relazione può essere dedotta dalle equazioni di base dell'elettromagnetismo considerando i fenomeni di induzione elettromagnetica (legge di Faraday-Neumann-Lenz) e la relazione costitutiva del campo magnetico prodotto da un solenoide. Infatti essendo il campo magnetico B prodotto da un solenoide:
(con N numero di spire, ℓ lunghezza del solenoide, μ permeabilità magnetica del mezzo posto all'interno al solenoide ed I intensità di corrente che vi scorre) se la corrente I che scorre nel solenoide/induttore è variabile nel tempo, anche B sarà variabile nel tempo. Essendo B variabile nel tempo, si produce una variazione di flusso del campo magnetico concatenato con il solenoide stesso il che produce, per la legge di Faraday-Neummann-Lenz, una f.e.m. auto-indotta ai capi dell'induttore. Questa differenza di potenziale indotta si oppone, per la legge di Lenz, alla causa che l'ha generata ovvero alla corrente variabile che scorre inizialmente sull'induttore (tramite quindi una corrente di segno opposto) da cui l'opposizione dell'induttore alle variazioni di corrente stessa, ed è questo il motivo per cui ai capi dell'induttore viene collegato il diodo volano quando si vuole eliminare la componente residua di segno opposto, infatti l'energia elettrica iniziale perduta viene immagazzinata sotto forma di energia del campo magnetico nel solenoide/induttore e poi nuovamente rilasciata in forma di energia elettrica (corrente) di segno opposto al cessare dell'alimentazione elettrica dell'induttore, da cui l'aggettivo di elemento 'reattivo' riferito a tale componente.
L'ampiezza della f.e.m. è correlata con l'intensità della corrente e con la frequenza delle sinusoidi dalla seguente equazione:
dove è la pulsazione della sinusoide legata alla frequenza dalla relazione . Si definisce reattanza induttiva (dimensionalmente uguale alla resistenza ed alla reattanza capacitiva):
La reattanza induttiva è la componente immaginaria positiva dell'impedenza. In termini di fasore, definita l'unità immaginaria, l'impedenza di un induttore è data da:
A meno di fenomeni parassiti come dissipazioni presenti nei casi reali, l'induttore ideale ha quindi impedenza puramente immaginaria pari alla sua reattanza indicando con essa la sua capacità di immagazzinare energia magnetica.
Reti di induttori[modifica | modifica wikitesto]
Se vi sono più induttori in parallelo nell'ipotesi che la mutua induzione tra di loro sia trascurabile, sono equivalenti ad un unico induttore con induttanza equivalente (Leq):
Infatti la corrente che viene iniettata su tale rete si distribuisce tra i vari induttori in maniera tale che i prodotti delle loro induttanze per le correnti che li attraversano siano eguali. Questo in virtù del fatto che se la corrente iniettata varia nel tempo, la differenza di potenziale ai capi dei vari induttori deve essere eguale.
Se consideriamo induttori in serie la corrente che li attraversa è la stessa, se la loro mutua induzione è trascurabile, il flusso concatenato all'insieme degli induttori è pari alla somma del flusso concatenato ad ogni singolo elemento.
Ne segue:
Applicazioni[modifica | modifica wikitesto]
Un induttore assomiglia ad un elettromagnete come struttura, ma è usato per uno scopo diverso: immagazzinare energia in un campo magnetico.
Un'applicazione molto comune è negli alimentatori a commutazione (ad esempio: gli alimentatori per computer) che, rispetto agli alimentatori tradizionali lineari, hanno un rendimento maggiore.
Per la loro capacità di modificare i segnali in corrente alternata, gli induttori sono usati nell'elettronica analogica e nel trattamento dei segnali elettrici, incluse le trasmissioni via etere.
Visto che la reattanza induttiva XL cambia con la frequenza, un filtro elettronico può usare induttori assieme a condensatori ed altri componenti per filtrare parti specifiche dello spettro di frequenza di un segnale. Due o più induttori (con il campo magnetico in comune) costituiscono un trasformatore comunemente usato sia negli apparati elettronici che in elettrotecnica.
Fattore Q[modifica | modifica wikitesto]
Un induttore ideale non presenta fenomeni dissipativi: l'energia immagazzinata nel campo magnetico viene restituita integralmente. In un induttore reale la corrente percorre un filo conduttore, con una sua resistenza, e genera un campo magnetico che attraversa il nucleo (se presente) ed eventuali altri oggetti nelle vicinanze (schermature o altro). La resistenza nel filo a frequenze elevate aumenta per l'effetto pelle, proporzionale in modo approssimativo con la radice quadrata della frequenza. Il nucleo ed eventuali materiali magnetici nelle vicinanze hanno un'isteresi che determina perdite proporzionali alla frequenza e correnti parassite proporzionali con il quadrato della frequenza. Se i materiali vicini sono conduttori avremo solo perdite per correnti parassite (proporzionali al quadrato della corrente). Tutto questo viene indicato mediante un fattore di qualità Q (in inglese: Q factor):
Più grande è il suo valore, migliore è il rendimento dell'induttore. In pratica è una funzione piuttosto complessa della frequenza (la frequenza compare al numeratore in ω, la pulsazione, ma la resistenza R che compare al denominatore è, come detto, fortemente legata ad essa). Si dovrà scegliere l'induttore in corrispondenza del massimo di questa funzione. In tutto questo non si è tenuto conto dei fenomeni di saturazione (corrente troppo intensa) che determinano un crollo dell'induttanza e quindi del fattore Q e che vanno anche tenuti presenti nella scelta dell'induttore.
Formule per il calcolo dell'induttanza[modifica | modifica wikitesto]
1. Solenoide con nucleo magnetico chiuso:
- RB: Riluttanza totale
- μ:Permeabilità magnetica assoluta del nucleo
- N: numero di spire
- A: area della sezione del nucleo magnetico
- l: lunghezza del nucleo
2. Filo conduttore rettilineo in aria:
- l = lunghezza del conduttore
- d = diametro del conduttore
Quindi se un conduttore lungo 10 mm con un diametro di 1 mm ha un'induttanza di circa 5,38 nH lo stesso filo lungo 100 mm ha un'induttanza di 100 nH.
3. Solenoide corto cilindrico senza nucleo magnetico:
- (è disponibile un calcolatore on line. Vedi nota:[2])
- r = raggio esterno dell'avvolgimento in pollici
- l = lunghezza dell'avvolgimento in pollici
- N = numero di spire
4. Induttore cilindrico a più strati in aria (senza nucleo magnetico):
- r = raggio medio dell'avvolgimento in pollici
- l = lunghezza degli avvolgimenti in pollici
- N = numero di spire
- d = spessore degli avvolgimenti (cioè raggio esterno meno raggio interno)
5. Filo a spirale piatta senza nucleo magnetico:
- r = raggio medio della spirale
- N = numero di spire
- d = spessore dell'avvolgimento (cioè raggio esterno meno raggio interno)
Quindi un avvolgimento a spirale di 8 spire, raggio medio di 25 mm e spessore di 10 mm dovrebbe avere un'induttanza di 5,13 µH.
6. Induttanza di un avvolgimento su un materiale magnetico di forma toroidale (di sezione circolare) di cui sia nota la permeabilità magnetica relativa :
- μ = permeabilità assoluta del nucleo magnetico
- N = numero di spire
- r = raggio dell'avvolgimento
- D = diametro totale del toroide
Le formule riportate sopra danno risultati approssimativi (specialmente la seconda, quella di un filo conduttore diritto). La più precisa è la sesta che si riferisce ad un induttore toroidale.
Va notato che, negli avvolgimenti circolari, l'induttanza è proporzionale al quadrato del numero delle spire. Questo è utile nella pratica perché, nota l'induttanza ed il numero di spire di un induttore, si può facilmente modificarne l'induttanza variando il numero di spire con una discreta precisione.
Storia[modifica | modifica wikitesto]
Nel 1885, William Stanley, Jr. realizzò il primo induttore basandosi su un'idea di Lucien Gaulard e John Gibbs. Era il precursore del moderno trasformatore.
Galleria d'immagini[modifica | modifica wikitesto]
Immagini di induttori per circuiti stampati:
-
Induttore per circuito stampato
-
Vista esplosa dello stesso induttore
-
Induttore per circuito stampato con le spire realizzate sul circuito stampato stesso
-
Vista esplosa dello stesso induttore
Varie forme di nuclei magnetici per induttanze (immagini realizzate al computer):
-
Nucleo C
-
Nucleo U
-
Nucleo E
-
Nucleo ER
-
Nucleo EFD
-
Nucleo toroidale
-
Nucleo EP
-
Nucleo RM
Note[modifica | modifica wikitesto]
Voci correlate[modifica | modifica wikitesto]
- Condensatore (elettrotecnica)
- Induttanza
- Autoinduzione
- Mutua induzione
- Legge di Lenz
- Elettromagnete
- Convertitore buck
- Convertitore boost
- Convertitore buck-boost
- Convertitore DC-DC
- Fattore Q
- Induzione elettromagnetica
- Circuito RL
- Circuito RLC
- Trasformatore
- Giratore
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «induttore»
Wikizionario contiene il lemma di dizionario «induttore» Wikimedia Commons contiene immagini o altri file su induttore
Wikimedia Commons contiene immagini o altri file su induttore
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) inductor, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- [1]
| Controllo di autorità | Thesaurus BNCF 24537 · LCCN (EN) sh85041716 · GND (DE) 4182601-2 · J9U (EN, HE) 987007536062305171 |
|---|