Convertitore ad accumulo elevatore

Un convertitore ad accumulo elevatore[1] o boost (o convertitore step-up) è un convertitore DC-DC con una tensione di uscita maggiore dell'ingresso. È una classe di alimentatori a commutazione contenenti almeno due commutatori a semiconduttore (un diodo e un transistor) e almeno un elemento accumulatore di energia. Filtri composti da combinazioni di induttori e capacità sono spesso aggiunti ad un convertitore boost per migliorarne le caratteristiche.
Panoramica[modifica | modifica wikitesto]
La tensione di una presa elettrica non può alimentare direttamente dispositivi come computer, orologi digitali o telefoni. La presa fornisce corrente alternata mentre il dispositivo richiede corrente continua. La conversione di potenza permette a dispositivi alimentabili in cc di utilizzare potenza proveniente da una sorgente in ca. Un dispositivo chiamato raddrizzatore è in grado di convertire una tensione ca in cc.
L'alimentazione cc può essere anche fornita direttamente da batterie, pannelli solari fotovoltaici generatori in cc. Il processo che converte una tensione cc in un'altra tensione cc viene chiamato conversione cc-cc o anche conversione dc-dc usando la sigla inglese per la corrente continua.
Un convertitore boost è un convertitore DC-DC con una tensione d'uscita maggiore di quella in ingresso. Un convertitore boost viene spesso chiamato anche convertitore step-up, (da step=gradino in inglese) ossia circuito "innalzatore di tensione" dato che esso "eleva" la tensione in ingresso. Dato che la potenza (V*I) deve conservarsi, la corrente di uscita sarà sempre una frazione di quella in ingresso, in genere all'incirca inversamente proporzionale al fattore di elevazione della tensione in uscita, tolte le perdite.
Storia[modifica | modifica wikitesto]
Per problemi di efficienza, il commutatore deve aprire e chiudere il circuito molto velocemente e avere poche perdite. L'avvento di commutatori a semiconduttore nei primi anni del 1950 ha rappresentato un passo fondamentale dato che ha in pratica reso possibile l'esistenza dei convertitori come il boost. I commutatori a semiconduttore si accendono e spengono velocemente e durano più a lungo rispetto ad altri commutatori come quelli a valvole o a relè. I primi convertitori cc-cc furono sviluppati nei primi anni del 1960 non appena divennero reperibili i primi commutatori a semiconduttore. La domanda nell'industria aerospaziale di convertitori piccoli, leggeri e efficienti ha provocato lo sviluppo di questa tecnologia.
I sistemi a commutazione come gli alimentatori switching sono una sfida per il progettista dato che il funzionamento del modello del circuito dipende dal fatto che il commutatore sia aperto o chiuso.
R.D. Middlebrook del Caltech nel 1977 pubblicò i modelli per i convertitori dc-dc in uso oggigiorno. Middlebrook fece una media della configurazione circuitale per ogni stato del commutatore usando una tecnica chiamata media dello spazio di stato (o state-space averaging). Questa semplificazione ha ridotto i due sistemi in uno. Il nuovo modello risultante portò alla comprensione delle equazioni di progettazione che sono state utili sino ad oggi alla crescita dei sistemi SMPS (Switched-mode power supply).
Applicazioni[modifica | modifica wikitesto]

I sistemi alimentati a batterie spesso sono costituiti da molte celle poste in serie per ottenere tensioni più elevate. Non è sempre possibile, per mancanza di spazio o per questioni di peso, mettere in serie tante batterie soprattutto nelle applicazioni dove è richiesta alta tensione. I convertitori boost possono aumentare la tensione e ridurre di conseguenza il numero di celle necessarie a questo scopo. Due tipiche applicazioni a batterie che usano i convertitori boost sono i veicoli elettrici ibridi (HEV) e i sistemi di illuminazione.
La Toyota Prius contiene un motore che usa tensioni di circa 500 V. Senza un convertitore boost, la Prius necessiterebbe di 417 batterie per alimentare il suo motore elettrico. In realtà la Prius usa solo 168 batterie e quindi eleva la tensione delle batterie da 202 V a 500 V. I convertitori boost alimentano anche dispositivi di scala molto più piccola, come i sistemi di illuminazione portatili. Un LED bianco richiede tipicamente 3.3V per emettere luce, e un convertitore boost può innalzare la tensione di una singola cella alcalina da 1.5 V per alimentare la lampada. I convertitori boost possono produrre anche tensioni più elevate per far funzionare i tubi fluorescenti a catodo freddo (CCFL) in dispositivi come retro illuminatori di LCD e lampade flash.
Analisi del circuito[modifica | modifica wikitesto]
Principio di funzionamento[modifica | modifica wikitesto]
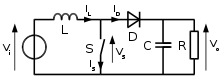

Il principio base di funzionamento di un convertitore boost consiste in due stati distinti (vedere figura 2):
- nello stato "on", il commutatore S (vedere figura 2) è chiuso, provocando un aumento di corrente nell'induttore;
- nello stato "off", il commutatore è aperto e l'unico percorso offerto alla corrente dell'induttore è attraverso il diodo D, la capacità C e il carico R. Ciò provoca il trasferimento dell'energia accumulata durante lo stato "on" dall'induttore verso la capacita'.
Modo di funzionamento continuo[modifica | modifica wikitesto]

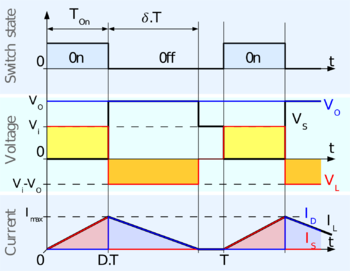
Quando un convertitore boost opera in modo continuo, la corrente che passa attraverso l'induttore (IL) non scende mai a zero. La figura 3 mostra le forme d'onda tipiche di corrente e tensione in un convertitore operante in questa modalità. La tensione di uscita può essere calcolata come segue, nel caso di un convertitore ideale (cioè usando componenti con un comportamento ideale) operante in condizioni stazionarie:
Durante lo stato di funzionamento acceso (on), il commutatore S è chiuso e la tensione di ingresso (Vi) appare ai capi dell'induttore; ciò provoca un cambiamento nella corrente (IL) che scorre attraverso l'induttore durante il periodo di tempo (t). Questo funzionamento viene descritto dalla formula:
Alla fine dello stato 'on' (acceso) l'incremento di IL è perciò:
D è il duty cycle: esso rappresenta la frazione del periodo di commutazione T in cui l'interruttore è chiuso. D varia pertanto da 0 (interruttore sempre aperto) a 1 (interruttore sempre chiuso).
Durante lo stato di 'off' (spento), il commutatore S è aperto, perciò la corrente dell'induttore fluisce attraverso il carico. Se consideriamo la caduta di tensione attraverso il diodo idealmente uguale a zero, e una capacità abbastanza grande da mantenere la sua tensione costante, l'evoluzione di IL è:
Perciò, la variazione di IL durante il periodo di spento è:
Se consideriamo che il convertitore operi in condizioni stabili, l'ammontare dell'energia accumulata in ogni suo componente deve essere la stessa all'inizio e alla fine del ciclo di commutazione. In particolare, l'energia immagazzinata nell'induttore è data da:
Perciò, è ovvio che la corrente dell'induttore deve essere la stessa all'inizio e alla fine del ciclo di commutazione. Questo può essere scritto come:
Sostituendo e con le loro espressioni si ottiene:
Questo può essere scritto come:
Dall'espressione precedente si può vedere che la tensione di uscita è sempre maggiore di quella di ingresso (come il duty cycle va da 0 a 1), e che essa cresce con D, teoricamente all'infinito come D raggiunge il valore di 1. Questa è la ragione per la quale questo convertitore viene spesso chiamato convertitore step-up (trad. gradino in alto).
Modo di funzionamento discontinuo[modifica | modifica wikitesto]
In molti casi, l'ammontare dell'energia richiesta dal carico è abbastanza piccola da essere trasferita in un tempo più piccolo della durata dell'intero ciclo di commutazione. In questo caso, la corrente che passa attraverso l'induttore cade a zero durante parte del periodo. L'unica differenza nel principio descritto in precedenza è che l'induttore viene completamente scaricato alla fine del ciclo di commutazione (vedere le forme d'onda presenti in figura 4). Malgrado piccola, la differenza ha un grande effetto sull'equazione della tensione di uscita. Essa può essere calcolata nel modo seguente:
Dato che la corrente nell'induttore all'inizio del ciclo è zero, il suo valore massimo (a t=D.T) è:
Durante il periodo di off, IL cade a zero dopo δ.T:
Usando le due precedenti equazioni, δ è:
La corrente di carico Io è uguale alla corrente media del diodo (ID). Come si può osservare in figura 4, la corrente del diodo è uguale alla corrente nell'induttore durante lo stato off. Perciò la corrente in uscita può essere scritta come:
Sostituendo ILmax e δ con le loro rispettive espressioni si ottiene:
Perciò, il guadagno di tensione in uscita può essere scritto come:
Confrontata con l'espressione della tensione di uscita per la modalità continua, questa espressione è molto più complicata. Inoltre, in modalità discontinua, la tensione di uscita non dipende solo dal duty cycle, ma anche dal valore dell'induttore, dalla tensione in ingresso e dalla corrente in uscita.
Limite tra il modo di funzionamento continuo e discontinuo[modifica | modifica wikitesto]

Come detto all'inizio di questa sezione, il convertitore opera in modo discontinuo quando il carico assorbe bassa corrente, e in modo continuo a regimi di corrente di carico superiori. Il limite tra i modi discontinuo e continuo viene raggiunto quando la corrente dell'induttore cade a zero esattamente alla fine del ciclo di commutazione. Con le notazioni di figura 4, ciò corrisponde a:
In questo caso, la corrente di uscita Iolim (corrente di uscita al limite tra modo continuo e discontinuo) è data da:
Sostituendo ILmax dall'espressione data nella sezione modo discontinuo si ottiene:
Dato che Iolim è la corrente al limite tra modo continuo e discontinuo, essa soddisfa le espressioni di entrambe le modalità. Perciò, usando l'espressione della tensione di uscita in modo continuo, la precedente espressione si può scrivere anche come:
Introduciamo altre due notazioni:
- la tensione normalizzata, definita da . Essa corrisponde al guadagno in tensione del convertitore;
- la corrente normalizzata, definita da . Il termine è uguale all'incremento massimo della corrente dell'induttore durante un ciclo, cioè l'incremento della corrente dell'induttore con un duty cycle D=1. Perciò, in regime stazionario del convertitore, ciò significa che è uguale a 0 per corrente di uscita nulla, e 1 per la massima corrente che il convertitore può fornire.
Usando queste notazioni avremo che:
- in modo continuo, ;
- in modo discontinuo, ;
- la corrente al limite tra modo continuo e discontinuo è . Perciò, il punto limite tra modo continuo e discontinuo viene dato da:
Queste espressioni sono state tracciate in figura 5. Le differenza di comportamento tra modo continuo e discontinuo può essere chiaramente osservata. Ciò è molto importante dal punto di vista di un circuito di controllo.
Analisi dello stato spaziale medio (State Space Averaging Analysis)[modifica | modifica wikitesto]

L'analisi del modello medio (average model analysis) è un metodo per calcolare la media nel tempo delle forme d'onda in un circuito a commutazione. Esso consiste nello scrivere le equazioni corrispondenti ad ogni stato di lavoro del convertitore (in questo caso due stati: on e off, come mostrato in figura 2), e poi moltiplicarle per il tempo che il convertitore spende in ogni stato.
Nel caso del convertitore boost, durante lo stato di on, la rapidità di cambiamento della corrente nell'induttore è data da:
Nello stato off, la tensione ai capi del commutatore è uguale alla tensione di uscita (si assume una caduta di tensione uguale a zero nel diodo polarizzato direttamente):
Perciò, il tasso medio di cambiamento della corrente nell'induttore viene ottenuto moltiplicando le due precedenti equazioni per il tempo impiegato negli stati corrispondenti (DT nello stato on e (1-D) T nello stato off, assumendo che il convertitore operi in modo continuo) e dividendo per il periodo di commutazione:
È importante notare che rappresenta i cambiamenti nella corrente dell'induttore in una scala di tempo più lenta della frequenza di commutazione. Per un convertitore operante in modo continuativo, . Perciò la precedente equazione diventa:
Che può essere riscritta come
(stessa equazione di sopra)
L'aspetto interessante di questo metodo è che esso maschera il comportamento in commutazione del convertitore, permettendo l'uso delle tecniche classiche di analisi in corrente alternata e continua.
Circuito reale / non ideale[modifica | modifica wikitesto]
Effetti delle resistenze parassite[modifica | modifica wikitesto]

Nell'analisi precedente, non sono stati considerati gli elementi dissipativi di potenza, cioè le (resistenze). Ciò significa che la potenza viene trasmessa senza perdite dalla sorgente al carico. In realtà, esistono sempre delle resistenze parassite in tutti i circuiti reattivi, dovute alla resistività dei materiali di cui sono fatti i componenti che li compongono. Perciò, una frazione della potenza gestita dal convertitore, viene dissipata da queste resistenze parassite.
Per semplicità, consideriamo che l'induttore sia l'unico componente non ideale del circuito, e che sia equivalente ad un induttore ideale in serie ad una resistenza ideale. Quest'assunto è accettabile dato che un induttore è costituito solitamente da un lungo spezzone di filo avvolto, che è probabile che presenti una resistenza parassita non trascurabile (RL). Inoltre la corrente scorre attraverso l'induttore, sia durante lo stato acceso (on) che durante quello spento (off).
Usando il metodo state-space averaging, possiamo scrivere:
dove e sono rispettivamente la tensione media ai capi dell'induttore e del commutatore nel ciclo di commutazione. Se consideriamo che il convertitore operi in modo stazionario, la corrente media che passa attraverso l'induttore è costante. La tensione media ai capi dell'induttore è:
Quando il commutatore è in stato on, VS=0. Quando è in stato off, il diodo viene polarizzato direttamente (consideriamo il modo di funzionamento continuo), perciò VS=Vo. Dunque, la tensione media ai capi del commutatore sarà:
La corrente di uscita è uguale alla corrente nell'induttore durante lo stato off. La corrente media nell'induttore è dunque:
Assumendo che la corrente e la tensione di uscita abbiano ripple trascurabile, il carico del convertitore può essere considerato come puramente resistivo. Se R è la resistenza del carico, l'espressione sopra diventa:
Usando le precedenti equazioni, la tensione in ingresso diventa:
Questo può essere scritto come:
Se la resistenza nell'induttore è zero, la precedente equazione diventa uguale a quella del caso ideale. Ma come aumenta RL, il guadagno in tensione del convertitore diminuisce in confronto al circuito ideale. Inoltre, l'influenza di RL cresce con il duty cycle. Tutto ciò è descritto in figura 7.
Note[modifica | modifica wikitesto]
- ^ Gli alimentatori switching (PDF), su itiomar.it (archiviato dall'url originale il 24 luglio 2015).
Bibliografia[modifica | modifica wikitesto]
- Ned Mohan, Undeland, Tore M., Robbins, William P., Power Electronics, Hoboken, John Wiley & Sons, Inc., 2003, ISBN 0-471-42908-2.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sui convertitori ad accumulo elevatore
Wikimedia Commons contiene immagini o altri file sui convertitori ad accumulo elevatore
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Boost PFC Mathematical Calculations, su smps.com. URL consultato il 23 maggio 2007 (archiviato dall'url originale il 22 maggio 2008).
- (EN) Daycounter Switching Converter Power Supplies, su daycounter.com.
| Controllo di autorità | GND (DE) 7570977-6 |
|---|













































