Convertitore buck-boost

Convertitore buck-boost.

Con il termine convertitore riduttore-elevatore o buck-boost ci si può riferire a due diverse tipologie di convertitori DC-DC. Entrambe possono produrre una tensione maggiore (in valore assoluto) rispetto alla tensione di ingresso; possono altresì produrre una tensione di uscita che varia dal massimo valore possibile, fino quasi a zero.

1. Tipologia invertente: la tensione di uscita è di polarità opposta rispetto all'ingresso
2. Convertitore buck (riduttore o step-down) seguito da convertitore boost (elevatore o step-up): la tensione di uscita è della stessa polarità dell'ingresso, e può essere maggiore o minore in valore. Questo tipo di buck-boost non invertente può impiegare un singolo induttore utilizzato sia come induttore del buck e come induttore del boost.

Questa pagina si occupa di descrivere la topologia invertente.

Il convertitore buck-boost è una tipologia di convertitore DC-DC, che presenta una uscita continua di valore maggiore o minore del valore della tensione in ingresso. È un alimentatore che ha una topologia circuitale simile a quella del convertitore buck e del boost. Il livello dell'uscita può essere aggiustato agendo sul duty cycle del transistore che commuta. Uno dei possibili lati negativi di questo convertitore è il fatto che l'interruttore non abbia uno dei terminali a terra: questo complica la circuiteria di pilotaggio; inoltre, la polarità dell'uscita è opposta a quella dell'ingresso. Lo switch può essere posto sia al lato della terra, o su quello dell'alimentazione.

Principio di operazione

Fig 1: Schematico di un convertitore buck-boost.

Fig 2: I due stati di operazione di un buck-boost: quando l'interruttore è acceso, l'ingresso fornisce corrente all'induttore e la capacità fornisce corrente al resistore (carico di uscita). Quando l'interruttore è spento, l'energia dell'alimentazione è immagazzinata dell'induttanza, e l'induttore fornisce corrente al carico tramite il diodo D.

Il principio di base del buck-boost è mostrato in figura 2:

• in stato ON (interruttore chiuso), la tensione di ingresso è direttamente connessa all'induttore L; si accumula pertanto energia in L. In questo stadio, il condensatore fornisce energia al carico di uscita.
• in stato OFF (interruttore aperto), l'induttore è collegato all'uscita ed alla capacità, in modo da trasferire energia da L a C ed R.

Rispetto al convertitore buck e al boost, le caratteristiche del buck-boost sono principalmente:

• la polarità dell'uscita, opposta a quella dell'ingresso;
• l'uscita può variare in modo continuo da 0 a $-\infty$ (per un convertitore ideale). Le variazioni dell'uscita per un buck ed un boost sono rispettivamente da 0 a $V_{i}$ e da $V_{i}$ a $\infty$.

Funzionamento in modo continuo (CCM)

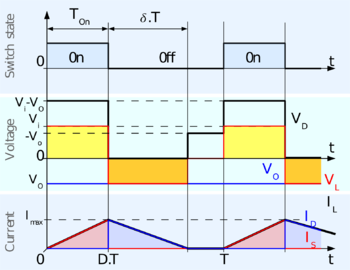
Se la corrente nell'induttore L non giunge mai a zero durante un ciclo di commutazione, si dice che il convertitore opera in continua (continuous current mode, CCM). Le forme d'onda di corrente e tensione in un convertitore ideale sono mostrate in figura 3.

Da $t=0$ a $t=D\,T$, il convertitore è in stato ON, e lo switch S è pertanto chiuso. La variazione di corrente nell'induttore (I_L) è data dalla relazione

${\frac {\operatorname {d} I_{\text{L}}}{\operatorname {d} t}}={\frac {V_{i}}{L}}$

Al termine della fase ON, l'incremento di I_L è:

$\Delta I_{{\text{L}}_{\text{On}}}=\int _{0}^{D\,T}\operatorname {d} I_{\text{L}}=\int _{0}^{D\,T}{\frac {V_{i}}{L}}\,\operatorname {d} t={\frac {V_{i}\,D\,T}{L}}$

D è il duty cycle: esso rappresenta la frazione del periodo di commutazione T in cui l'interruttore è chiuso. D varia pertanto da 0 (interruttore sempre aperto) a 1 (interruttore sempre chiuso).

Durante lo stato OFF, lo switch è aperto, quindi la corrente dell'induttore fluisce verso il carico. Se si suppone pari a zero la caduta di tensione sul diodo e si suppone un condensatore grande abbastanza da poter considerare la sua tensione costante, l'evoluzione di I_L è:

${\frac {\operatorname {d} I_{\text{L}}}{\operatorname {d} t}}={\frac {V_{o}}{L}}$

La variazione di I_L durante lo stato OFF è pertanto:

$\Delta I_{{\text{L}}_{\text{Off}}}=\int _{0}^{\left(1-D\right)T}\operatorname {d} I_{\text{L}}=\int _{0}^{\left(1-D\right)T}{\frac {V_{o}\,\operatorname {d} t}{L}}={\frac {V_{o}\left(1-D\right)T}{L}}$

Fig 3: Forme d'onda di corrente e tensione in un buck-boost operante in CCM.

Considerando il fatto che il convertitore opera in regime statico, l'energia immagazzinata in ognuno dei componenti deve essere la stessa all'inizio ed alla fine del ciclo di commutazione. Dato che l'energia dell'induttore deriva dalla relazione

$E={\frac {1}{2}}L\,I_{\text{L}}^{2}$

è ovvio che il valore di I_L al termine dello stato OFF deve essere lo stesso di I_L all'inizio dello stato ON, cioè la somma delle variazioni di I_L durante gli stati ON e OFF devono dare come risultato zero:

$\Delta I_{{\text{L}}_{\text{On}}}+\Delta I_{{\text{L}}_{\text{Off}}}=0$

Sostituendo $\Delta I_{{\text{L}}_{\text{On}}}$ e $\Delta I_{{\text{L}}_{\text{Off}}}$ con le loro espressioni, si ottiene:

$\Delta I_{{\text{L}}_{\text{On}}}+\Delta I_{{\text{L}}_{\text{Off}}}={\frac {V_{i}\,D\,T}{L}}+{\frac {V_{o}\left(1-D\right)T}{L}}=0$

La precedente espressione può essere riscritta come:

${\frac {V_{o}}{V_{i}}}=\left({\frac {-D}{1-D}}\right)$

il che significa che:

$D={\frac {V_{o}}{V_{o}-V_{i}}}$

Dalla precedente espressione, si può notare che la polarità dell'uscita è sempre negativa (dato che il duty cycle varia tra 0 e 1), e che il suo valore assoluto cresce con D, teoricamente fino a meno infinito, man mano che D tende a 1. A parte la polarità, questo convertitore è sia step-up (come un convertitore boost) che step-down (come un convertitore buck): questo è il motivo per cui ha nome buck-boost.

Regime discontinuo (DCM)

Fig 4: Forme d'onda di corrente e tensione in un buck-boost operante in regime discontinuo.

In alcuni casi il valore dell'energia richiesta dal carico è bassa abbastanza da poter essere trasferita in un periodo di tempo minore dell'intero periodo di commutazione. In tal caso, la corrente che scorre nell'induttore raggiunge lo zero durante il periodo. L'unica differenza nel principio di funzionamento sopra descritto è che l'induttore viene completamente scaricato al termine del ciclo di commutazione (vedi Fig.4); anche se lieve, la differenza ha un forte effetto sull'equazione della tensione di uscita, che può essere calcolata come segue:

Dato che la corrente nell'induttore all'inizio del ciclo è pari a zero, il suo valore massimo $I_{L_{\text{max}}}$ (in $t=D\,T$) è

$I_{L_{\text{max}}}={\frac {V_{i}\,D\,T}{L}}$

Durante il periodo OFF, I_L torna a zero dopo δ.T:

$I_{L_{\text{max}}}+{\frac {V_{o}\,\delta \,T}{L}}=0$

Utilizzando le due precedenti equazioni,

$\delta =-{\frac {V_{i}\,D}{V_{o}}}$

La corrente nel carico $I_{o}$ è uguale alla corrente media nel diodo ($I_{D}$). Come si può vedere dalla figura 4, la corrente del diodo è pari a quella dell'induttore durante il periodo OFF; pertanto, si può scrivere la corrente di uscita come

$I_{o}={\bar {I_{D}}}={\frac {I_{L_{\text{max}}}}{2}}\delta$

Sostituendo $I_{L_{\text{max}}}$ e δ con le loro rispettive espressioni, si ha

$I_{o}=-{\frac {V_{i}\,D\,T}{2L}}{\frac {V_{i}\,D}{V_{o}}}=-{\frac {V_{i}^{2}\,D^{2}\,T}{2L\,V_{o}}}$

Pertanto la tensione di uscita può essere espressa come segue:

${\frac {V_{o}}{V_{i}}}=-{\frac {V_{i}\,D^{2}\,T}{2L\,I_{o}}}$

Comparando all'espressione dell'uscita per il modo continuo, questa espressione è molto più complicata. Inoltre, in regime discontinuo, la tensione di uscita non dipende solo dal duty cycle, ma anche dal valore dell'induttanza, dalla tensione di ingresso e dalla corrente di uscita.

Limite tra CCM e DCM

Fig 5: Evoluzione della tensione di uscita normalizzata con la corrente di uscita normalizzata in un buck-boost.

Come già detto, il convertitore opera in regime discontinuo quando il carico assorbe una bassa corrente, e in continua a più alti livelli di corrente assorbita. Il limite tra modo continuo e discontinuo viene raggiunto quando la corrente dell'induttore raggiunge lo zero esattamente al termine del ciclo di commutazione. Con le notazioni in figura 4, questo corrisponde a:

$D\,T+\delta \,T=T$

$D+\delta =1$

In questo caso, la corrente di uscita $I_{o_{\text{lim}}}$ (corrente di uscita al limite tra regime continuo e discontinuo) è data dalla relazione

$I_{o_{\text{lim}}}={\bar {I_{D}}}={\frac {I_{L_{\text{max}}}}{2}}\left(1-D\right)$

Sostituendo $I_{L_{\text{max}}}$ con l'espressione fornita per il modo discontinuo, si ha

$I_{o_{\text{lim}}}={\frac {V_{i}\,D\,T}{2L}}\left(1-D\right)$

Dato che $I_{o_{\text{lim}}}$ è la corrente al limite tra CCM e DCM, essa soddisfa le equazioni di entrambi i modi di funzionamento. Pertanto, utilizzando l'espressione della tensione di uscita in CCM, la precedente espressione può essere riscritta come

$I_{o_{\text{lim}}}={\frac {V_{i}\,D\,T}{2L}}{\frac {V_{i}}{V_{o}}}\left(-D\right)$

Si introducano ora due ulteriori notazioni:

• tensione normalizzata, definita come $\left|V_{o}\right|={\frac {V_{o}}{V_{i}}}$, che corrisponde al guadagno in tensione del convertitore
• corrente normalizzata, definita come $\left|I_{o}\right|={\frac {L}{T\,V_{i}}}I_{o}$. Il termine ${\frac {T\,V_{i}}{L}}$ è pari al massimo incremento della corrente dell'induttore in un ciclo, cioè l'incremento della corrente nell'induttore con un duty cycle D=1. Perciò, se il convertitore opera in regime stazionario, significa che $\left|I_{o}\right|$ non è mai uguale 0 per nessun valore della corrente di uscita, e uguale a 1 per il valore massimo della corrente che il convertitore può erogare.

Utilizzando queste notazioni, si ottiene:

• in CCM, $\left|V_{o}\right|=-{\frac {D}{1-D}}$;
• in DCM, $\left|V_{o}\right|=-{\frac {D^{2}}{2\left|I_{o}\right|}}$;
• la corrente al limite tra CCM e DCM vale $I_{o_{\text{lim}}}={\frac {V_{i}\,T}{2L}}D\left(1-D\right)={\frac {I_{o_{\text{lim}}}}{2\left|I_{o}\right|}}D\left(1-D\right)$. Pertanto, il limite tra CCM e DCM è dato dalla relazione ${\frac {1}{2\left|I_{o}\right|}}D\left(1-D\right)=1$.

Tali espressioni sono raffigurate in figura 5; si può vedere chiaramente la differenza di andamento tra modo continuo (CCM) e modo discontinuo (DCM).

Circuito non ideale

Effetto delle resistenze parassite

Fig 6: evoluzione della tensione di uscita in un convertitore buck-boost in funzione del duty-cycle, al crescere della resistenza parassita dell'induttore.

Nell'analisi effettuata sopra, non sono stati considerati elementi dissipativi (resistori). Ciò significa che la potenza viene trasmessa senza perdite dall'ingresso verso l'uscita. Tuttavia, le resistenze parassite esistono in ogni circuito, a causa della resistività dei materiali con cui sono costruiti; pertanto, una frazione della potenza gestita dal convertitore è dissipata attraverso gli elementi parassiti.

Per semplicità, si considera qui che l'unico elemento non ideale sia l'induttore, e che il suo equivalente reale sia pertanto rappresentato da un induttore ideale con una resistenza serie. Questa ipotesi risulta accettabile, in quanto un'induttanza è realizzata tramite un lungo avvolgimento di filo, che mostra pertanto una resistenza parassita (R_L) non trascurabile. Inoltre, la corrente scorre nell'induttore sia nello stato ON che nella fase OFF.

Utilizzando la media, si può scrivere:

$V_{i}={\bar {V}}_{\text{L}}+{\bar {V}}_{S}$

in cui ${\bar {V}}_{\text{L}}$ e ${\bar {V}}_{S}$ sono rispettivamente la tensione media che cade sull'induttore e sull'interruttore durante il ciclo di commutazione. Se si considera che il convertitore operi in regime stazionario, la corrente media attraverso l'induttore risulta costante; la tensione media, invece, è:

${\bar {V}}_{\text{L}}=L{\frac {\bar {dI_{\text{L}}}}{dt}}+R_{\text{L}}{\bar {I}}_{\text{L}}=R_{\text{L}}{\bar {I}}_{\text{L}}$

Quando l'interruttore è chiuso, $V_{S}=0$; quando è aperto, il diodo è polarizzato in diretta (si considera di operare in CCM), pertanto $V_{S}=V_{i}-V_{o}$. Quindi, la tensione media che cade sull'interruttore è:

${\bar {V}}_{S}=D\,0+(1-D)(V_{i}-V_{o})=(1-D)(V_{i}-V_{o})$

La corrente di uscita è opposta a quella dell'induttore durante la fase OFF; la corrente media dell'induttore è quindi:

${\bar {I}}_{\text{L}}={\frac {-I_{o}}{1-D}}$

Supponendo che la corrente e la tensione di uscita abbiano un ripple trascurabile, il carico del convertitore può essere considerato puramente resistivo. Se R è la resistenza del carico, l'ultima espressione diviene

${\bar {I}}_{\text{L}}={\frac {-V_{o}}{(1-D)R}}$

Utilizzando le precedenti equazioni, la tensione di ingresso diventa

$V_{i}=R_{\text{L}}{\frac {-V_{o}}{(1-D)R}}+(1-D)(V_{i}-V_{o})$

Si può quindi riscrivere:

${\frac {V_{o}}{V_{i}}}={\frac {-D}{{\frac {R_{\text{L}}}{R(1-D)}}+1-D}}$

Se la resistenza dell'induttore è nulla, quest'ultima equazione torna ad essere uguale a quella del caso ideale. Al crescere di R_L, però, il guadagno di tensione del convertitore diminuisce rispetto al caso ideale. Inoltre, l'influenza di R_L aumenta all'aumentare del duty-cycle; questo effetto è raffigurato in figura 6.

Bibliografia

• Daniel W. Hart, "Introduction to Power Electronics", Prentice Hall, Upper Saddle River, New Jersey USA, 1997 ISBN 0-02-351182-6
• Christophe Basso, Switch-Mode Power Supplies: SPICE Simulations and Practical Designs. McGraw-Hill. ISBN 0-07-150858-9.

Voci correlate

• Convertitore buck
• Convertitore boost
• Convertitore DC-DC

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sui convertitori buck-boost