Coefficiente di Gini

Il coefficiente di Gini, introdotto dallo statistico italiano Corrado Gini[1], è una misura della diseguaglianza di una distribuzione. È spesso usato come indice di concentrazione per misurare la diseguaglianza nella distribuzione del reddito o anche della ricchezza. È un numero compreso tra 0 ed 1. Valori bassi del coefficiente indicano una distribuzione abbastanza omogenea, con il valore 0 che corrisponde alla pura equidistribuzione, ad esempio la situazione in cui tutti percepiscono esattamente lo stesso reddito; valori alti del coefficiente indicano una distribuzione più diseguale, con il valore 1 che corrisponde alla massima concentrazione, ovvero la situazione dove una persona percepisca tutto il reddito del paese mentre tutti gli altri hanno un reddito nullo.
Definizione[modifica | modifica wikitesto]
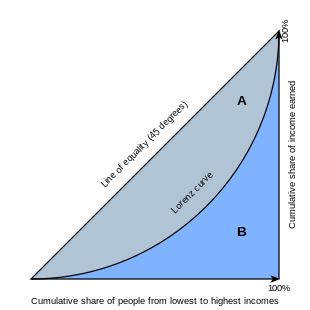
Il grafico mostra che il coefficiente di Gini è pari all'area indicata come A divisa per la somma delle aree indicate come A e B, cioè, G = A / (A + B). È anche pari a 2A e a 1 - 2B a causa del fatto che A + B = 0,5 (poiché i 2 assi vanno da 0 a 1).
La definizione matematica del coefficiente di Gini si basa sulla curva di Lorenz della distribuzione ed è legata all'area compresa fra la linea di perfetta uguaglianza e la curva di Lorenz[2]. Il coefficiente di Gini è definito come il rapporto fra l'area compresa tra la linea di perfetta uguaglianza e la curva di Lorenz () e l'area totale sotto la linea di perfetta uguaglianza (), ossia . Siccome l'intervallo sull'asse va da 0 a 1, allora e dunque il coefficiente di Gini è anche uguale a .
Perché esso sia correttamente definito, la variabile in considerazione non deve assumere valori negativi. Ad esempio, se si applica alla valutazione nella distribuzione della ricchezza, non si può dare il caso di individui a ricchezza negativa.
Si può incontrare la notazione con indice di Gini espresso in percentuale (0% - 100%), ovvero anche tra 0 e 100.
L'indice di Gini può anche essere definito in maniera indipendente dalla curva di Lorenz. L'indice di Gini è infatti pari alla metà della differenza media assoluta divisa per la media dei valori; questa divisione è necessaria per normalizzare l'indice.
Calcolo[modifica | modifica wikitesto]
Se la curva di Lorenz è rappresentata dalla funzione , il valore di B può essere ricavato attraverso l'integrazione:
In alcuni casi, questa equazione può essere utilizzata per calcolare il coefficiente di Gini senza conoscere direttamente la curva di Lorenz. Per esempio:
- Per una popolazione con valori yi, i = 1 fino a n, che sono indicizzati in modo non decrescente ( yi ≤ yi+1):
- Per una distribuzione di probabilità discreta f(y), dove yi, i = 1 a n, sono i punti con probabilità diversa da zero e che sono indicizzati in ordine crescente ( yi < yi+1):
- dove:
- and
- Per una funzione di distribuzione cumulativa F(y) differenziabile a tratti, che abbia media , e sia zero per tutti i valori negativi di y:[senza fonte]
Dato che il coefficiente di Gini è uguale alla metà della differenza relativa media, può anche essere calcolato ricorrendo alle formule per ricavare la differenza media relativa, indipendentemente dalla curva di Lorenz. L'indice di Gini è infatti pari alla metà della Differenza media assoluta divisa per la media dei valori; questa divisione è necessaria per normalizzare l'indice.
Per una popolazione discreta con valori yi, i = 1, ..., n, il coefficiente di Gini G è dato da:
Per una distribuzione di probabilità continua f(x), si ha invece la seguente formula:
Per un campione casuale S composto dai valori yi, i = 1 fino a n, che siano indicizzati in ordine non decrescente ( yi ≤ yi+1), la statistica:
è uno stimatore consistente della popolazione del coefficiente di Gini, ma non è, in generale, privo di bias. Come per la differenza media relativa, non esiste un campione statistico che in generale sia uno stimatore privo di pregiudizio statistico per la popolazione del coefficiente di Gini. Gli intervalli di confidenza per la popolazione del coefficiente di Gini possono essere calcolati con tecniche di bootstrap.
È possibile che in alcuni casi l'intera curva di Lorenz non sia nota, e siano conosciuti solo i valori in alcuni intervalli. In questo caso, il coefficiente di Gini può essere approssimato usando diverse tecniche per l'interpolazione e l'estrazione dei valori mancanti della curva di Lorenz. Se sono i punti noti sulla curva di Lorenz, con indicizzati in modo crescente (), si ha che:
- è la proporzione cumulata della variabile della popolazione, per con .
- è la proporzione cumulata della variabile di reddito, for con .
Se la curva di Lorenz è approssimata in ciascun intervallo come una linea tra due punti noti consecutivi, allora l'area può essere approssimata a dei trapezi e:
è l'approssimazione per . Si possono ottenere risultati più accurati utilizzando altri metodi di integrazione numerica per la stima dell'area , come ad esempio approssimando la curva di Lorenz con una funzione quadratica tra le coppie di intervalli noti, o costruendo una approssimazione appropriata che colleghi in modo appropriato tutti i punti noti della curva di Lorenz. Se la popolazione media e i valori al contorno di ciascun intervallo sono noti, questi dati possono essere utilizzati per migliorare l'accuratezza della approssimazione.
Coefficiente di Gini relativo al reddito nel mondo[modifica | modifica wikitesto]

Osservando la mappa mondiale del coefficiente di Gini sul reddito, si nota che i paesi scandinavi sono quelli dove il reddito è più equamente distribuito. Seguono la Germania, l'Austria, il Belgio, ecc. La maggior parte delle nazioni Europee sviluppate ha coefficienti di Gini compresi tra 0,24 e 0,36. Questo è anche il valore di Australia e Canada. Il coefficiente di Gini degli Stati Uniti d'America invece supera 0,4, indicando una maggiore diseguaglianza di reddito nella popolazione statunitense.
Tuttavia si deve tenere presente che il coefficiente di Gini può essere fuorviante quando si facciano paragoni tra i paesi geograficamente grandi e i piccoli (vedi la sezione dedicata alle critiche); il coefficiente di Gini, infatti, misurato per paesi geograficamente molto grandi, risulta generalmente molto più alto rispetto a ciascun coefficiente calcolato per le sue regioni. Infatti il coefficiente di Gini tiene conto anche delle diseguaglianze regionali, oltre che di quelle locali, all'interno di una stessa popolazione. Per questa ragione i punteggi calcolati per i Paesi europei sono difficilmente comparabili con il punteggio totalizzato dagli Stati Uniti o dalla Cina.
L'uso del coefficiente di Gini può aiutare nella quantificazione delle differenze nella politica e nella filosofia adottate per il benessere e per gli stipendi.
Coefficiente di Gini negli USA nel tempo[modifica | modifica wikitesto]

Il coefficiente di Gini per gli Stati Uniti d'America in diversi periodi di tempo è riportato qui a fini comparativi (fonte US Census Bureau):
Vantaggi per la misura dell'uguaglianza[modifica | modifica wikitesto]
- Il coefficiente di Gini ha come vantaggio principale quello di misurare la disuguaglianza attraverso l'analisi di un rapporto, invece di usare una variabile che non rappresenti la maggior parte della popolazione, come ad esempio il reddito pro capite o il prodotto interno lordo
- Può essere utilizzato per confrontare le distribuzioni della ricchezza in diversi settori della popolazione o in diversi stati; ad esempio il coefficiente di Gini per le aree urbane è diverso da quello delle aree rurali in molti Paesi (sebbene, ad esempio, negli Stati Uniti siano quasi identici).
- È sufficientemente semplice da poter essere confrontato tra diversi stati e facilmente interpretato. Le statistiche legate al PIL sono spesso criticate dato che non rappresentano i cambiamenti di tutta la popolazione; il coefficiente di Gini dimostra come il reddito cambi per ricchi e poveri. Se il coefficiente di Gini sale insieme al PIL, significa che lo stato di povertà non sta cambiando per la maggior parte della popolazione.
- Il coefficiente di Gini può essere utilizzato per indicare come la distribuzione del reddito sia cambiata nel tempo in un dato Paese, rendendo possibile osservare se la disuguaglianza stia crescendo o diminuendo.
- Il coefficiente di Gini soddisfa quattro importanti principi:
- Anonimia: non importa chi siano quelli che guadagnano molto e quelli che guadagnano poco.
- Indipendenza di scala: il coefficiente di Gini non considera la dimensione dell'economia, come sia misurata, o quanto sia ricco o povero in media un Paese.
- Indipendenza dalla popolazione: non importa quanto sia grande la popolazione di un Paese.
- Principio di trasferibilità, detto anche principio di Pigou-Dalton: se il reddito (meno la differenza), fosse trasferito da una persona ricca a una povera (trasferimento progressivo) la distribuzione risulterebbe più equa.
Svantaggi per la misura della disuguaglianza[modifica | modifica wikitesto]
- Come gli altri indici di tipo relativo (calcolati dal rapporti di altre due grandezze), presenta il limite di restare invariato se i redditi dei più ricchi e dei più poveri aumentano nella stessa proporzione, e quindi di non tenere conto della forbice fra i valori assoluti, che in realtà aumenta. Ad esempio se l'individuo ‘A' possiede 10.000 dollari e l'individuo ‘B' 100.000 dollari ed entrambi raddoppiano il loro reddito, il Gini non cambia anche se il divario tra i due è salito da 90.000 a 180.000 dollari.
- Il coefficiente di Gini misurato per paesi geograficamente molto grandi risulta generalmente molto più alto rispetto a ciascun coefficiente calcolato per le sue regioni. Per questa ragione i punteggi calcolati per i Paesi europei sono difficilmente comparabili con il punteggio totalizzato dagli Stati Uniti, ad esempio.
- Comparare le distribuzioni di reddito tra stati diversi può essere difficoltoso perché i sistemi di beneficio possono cambiare. Per esempio, alcuni stati offrono benefici monetari, mentre altri offrono buoni pasto, che non possono essere tenuti in conto come reddito nella curva di Lorenz e quindi non sono presi in considerazione nel calcolo del coefficiente di Gini.
- La misura può dare risultati diversi se applicata agli individui o alle unità familiari. Quando le popolazioni non vengono misurate con definizioni consistenti il confronto non ha senso.
- La curva di Lorenz può sottostimare la reale disuguaglianza se le unità familiari più ricche possono usare il loro reddito in modo più efficiente delle unità familiari povere. Da un altro punto di vista, la misura dell'ineguaglianza potrebbe essere il risultato di una maggiore o minore efficienza nell'uso del reddito.
- Come per tutte le statistiche, ci saranno sempre sistematiche ed errori casuali nei dati. Il valore del coefficiente di Gini diminuisce quando i dati diventano meno accurati. Inoltre gli stati possono raccogliere i dati in modo diverso, rendendo difficile un confronto.
- Economie con redditi e coefficiente di Gini simili possono ancora avere distribuzioni di reddito molto diverse. Questo effetto è dovuto al fatto che le curve di Lorenz possono avere andamenti diversi dando comunque lo stesso risultato per G. Come esempio limite, una economia dove metà delle unità familiari non abbiano reddito, e l'altra metà si distribuisca l'intero reddito in modo equo ha un coefficiente di ½; ma un'economia con completa equità nella distribuzione del reddito, eccetto una unità familiare che abbia metà del reddito totale, ha anch'essa un coefficiente di Gini di ½.
- Si suppone che il coefficiente di Gini sia più sensibile al reddito delle classi medie che a quello degli estremi.
- Molto spesso si riporta il coefficiente di Gini senza descrivere le proporzioni dei quantili usati per le misure. Come per gli altri coefficienti di disuguaglianza, il coefficiente di Gini è influenzato dalla granularità delle misure. Per esempio, cinque quantili del 20% (bassa granularità) daranno un coefficiente di Gini più basso di 20 quantili del 5% ciascuno (alta granularità) presi dalla stessa distribuzione.
Come risultato di queste critiche, oltre o in competizione con il coefficiente di Gini sono utilizzate spesso misure di entropia (ad esempio gli indici Atkinson e Theil). Queste misure cercano di confrontare le distribuzioni delle risorse di giocatori intelligenti in un mercato con una distribuzione casuale con massima entropia, con quelle che sono ottenute considerando i giocatori come particelle non intelligenti che seguano le leggi della fisica statistica.
Coefficiente di Gini ottimale[modifica | modifica wikitesto]
In un loro studio[4], Giovanni Andrea Cornia e Julius Court (2001) giungono a suggerire politiche per il raggiungimento della distribuzione ottimale di ricchezza. Gli autori raccomandano di ricercare la moderazione anche per quanto riguarda la distribuzione della ricchezza cercando di tenersi lontani dai casi estremi. Sia un egualitarismo eccessivo che una grande diseguaglianza condurrebbero a una crescita lenta. Un eccessivo egualitarismo porta a incentivi-trappola, speculazione, grandi costi di operazione e corruzione nel sistema di redistribuzione, che limiterebbe il potenziale di crescita del Paese.
D'altra parte, una iniquità estrema diminuirebbe anch'essa il potenziale di crescita distruggendo la coesione sociale, aumentando il malcontento pubblico e alimentando il conflitto sociale, e causando incertezze riguardo ai diritti di proprietà. Quindi la politica pubblica deve avere come obbiettivo un "intervallo di inegualità efficiente". Gli autori sostengono che questo intervallo di efficienza sia rappresentato da valori del coefficiente di Gini compreso tra 0,25 (iniquità tipica dei paesi Nord europei) e 0,40 (quello di Paesi come la Cina e gli USA). Il profilo preciso della relazione tra iniquità e crescita riportata nella tabella varia, naturalmente, cambiando Paese dipendendo dalle risorse investite, la storia del Paese, eventuali livelli di povertà assoluta ancora presenti, e la quantità di programmi sociali presenti, così come dipende dalla distribuzione dei capitali fisici ed umani nel territorio.
Note[modifica | modifica wikitesto]
- ^ Gini 1912.
- ^ Lanza, pp. 188-200.
- ^ È da notare che l'indice utilizzato per gli Stati Uniti è cambiato nel 1992, facendo crescere il coefficiente di circa 0,02. Confronti tra i periodi precedenti e successivi a questo cambiamento possono essere fuorvianti. (dati ottenuti da US Census Bureau Archiviato il 6 ottobre 2006 in Internet Archive..)
- ^ (EN) Giovanni Andrea Cornia e Julius Court, Inequality, Growth and Poverty in the Era of Liberalization and Globalization, World Institute for Development Economics Research. Ospitato su ResearchGate.
Bibliografia[modifica | modifica wikitesto]
- (EN) P.M. Dixon, J. Weiner, T. Mitchell-Olds e R. Woodley, Bootstrapping the Gini coefficient of inequality, in Ecology, n. 68, 1987, pp. 1548-1551.
- Corrado Gini, Variabilità e mutabilità, 1912. Ristampato in E. Pizetti e T. Salvemini (a cura di), Memorie di metodologica statistica, Roma, Libreria Eredi Virgilio Veschi, 1955.
- (EN) Corrado Gini, Measurement of Inequality and Incomes, in The Economic Journal, vol. 31, 1921, pp. 124-126. Ospitato su archive.org.
- (EN) Xu Kuan, How Has the Literature on Gini's Index Evolved in the Past 80 Years? (PDF), Department of Economics, Dalhousie University, gennaio 2004. URL consultato il 1º giugno 2006.
- (EN) James Morgan, The Anatomy of Income Distribution, in The Review of Economics and Statistics, vol. 44, 1962, pp. 270-283.
- Giuseppe Lanza, La misurazione della disuguaglianza economica. Approcci, metodi e strumenti, Milano, Franco Angeli, 2015, ISBN 9788891711335.
- (EN) Joseph L. Gastwirth, The Estimation of the Lorenz Curve and Gini Index, in The Review of Economics and Statistics, vol. 54, 1972, pp. 306-316.
- (EN) Sudhir Anand, Inequality and Poverty in Malaysia, New York, Oxford University Press, 1983. Ospitato su archive.org.
- (EN) S. R. Chakravarty, Ethical Social Index Numbers, New York, Springer-Verlag, 1990.
- (EN) Robert Dorfman, A Formula for the Gini Coefficient, in The Review of Economics and Statistics, vol. 61, 1979, pp. 146-149. Ospitato su archive.org.
- (EN) Jeffrey A. Mills e Sourushe Zandvakili, Statistical Inference via Bootstrapping for Measures of Inequality, in Journal of Applied Econometrics, vol. 12, 1997, pp. 133-150.
- (EN) Malcolm Brown, Using Gini-Style Indices to Evaluate the Spatial Patterns of Health Practitioners: Theoretical Considerations and an Application Based on Alberta Data, in Social Science Medicine, vol. 38, 1994, pp. 1243-1256. Ospitato su archive.org.
Voci correlate[modifica | modifica wikitesto]
- Stati per uguaglianza di reddito
- Indice di sviluppo umano
- Stati per indice di sviluppo umano
- Stato sociale
- Variabile casuale paretiana
- Indice di concentrazione di Gini
- Indice di eterogeneità di Gini
- Indice Atkinson
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su coefficiente di Gini
Wikimedia Commons contiene immagini o altri file su coefficiente di Gini
Collegamenti esterni[modifica | modifica wikitesto]
- Coefficiente di Gini stimato dal Cia World Factbook, su cia.gov. URL consultato il 28 febbraio 2011 (archiviato dall'url originale il 13 giugno 2007).
- [1] Confronto del valore del coefficiente di Gini per aree rurali ed urbane. (EN)
- [2] World Income Inequality Database (EN)
- [3], Articolo di Forbes In praise of inequality (EN)
- (EN) mappa dei coefficienti di gini presa da WorldPolicy.org, su worldpolicy.org. URL consultato il 6 ottobre 2006 (archiviato dall'url originale il 1º settembre 2006).
- Software:
- Calcolatore gratis online Archiviato il 4 dicembre 2012 in Archive.is. calcola il coefficiente di Gini, disegna la curva di Lorenz e calcola molte altre misure di concentrazione dei dati forniti.
- Calcolatore gratis: script scaricabili e (in Python e Lua) per il calcolo delle disuguaglianze di Atkinson, Gini e Hoover.
- Gli utenti del software di analisi dei dati R possono installare il pacchetto "ineq" che consente di calcolare una vasta gamma di indici di disuguaglianza come quelli di Gini, Atkinson e Theil.
- (EN) A complete handhout about the Lorenz curve including various applications, including an Excel spreadsheet graphing Lorenz curves and calculating Gini coefficients as well as coefficients of variation.
| Controllo di autorità | J9U (EN, HE) 987007529599505171 · NDL (EN, JA) 01126754 |
|---|


























