Interpolazione
In matematica, e in particolare in analisi numerica, per interpolazione si intende un metodo per individuare nuovi punti del piano cartesiano a partire da un insieme finito di punti dati, nell'ipotesi che tutti i punti si possano riferire ad una funzione di una data famiglia di funzioni di una variabile reale.
Nelle attività scientifiche e tecnologiche, e in genere negli studi quantitativi di qualsiasi fenomeno, accade molto spesso di disporre di un certo numero di punti del piano ottenuti con un campionamento o con apparecchiature di misura e di ritenere opportuno individuare una funzione che passi per tutti i punti dati o almeno nelle loro vicinanze (vedi curve fitting).
Definizione del problema[modifica | modifica wikitesto]
Sia data una sequenza di n numeri reali distinti chiamati nodi e per ciascuno di questi sia dato un secondo numero . Ci proponiamo di individuare una funzione di una certa famiglia che sia in grado di descrivere una relazione tra l'insieme degli e quello degli , ovvero
- .
Una coppia viene chiamato punto dato ed viene detta funzione interpolante, o semplicemente interpolante, per i punti dati.
Talora i valori , quando si intendono riferiti a una funzione definita, si scrivono .
Esempio[modifica | modifica wikitesto]
Si supponga di avere la seguente tabella, che dà alcuni valori di una funzione che si può considerare nota in altra sede.

| 0 | 0 |
| 1 | 0,8415 |
| 2 | 0,9093 |
| 3 | 0,1411 |
| 4 | -0,33 |
| 5 | -0,9589 |
| 6 | -0,2794 |
L'interpolazione consente di stabilire il valore di per valori di compresi tra gli estremi dell'intervallo in esame ma che non sono tra quelli per cui è noto, ad esempio per .
Esistono molti metodi differenti di interpolazione; verranno di seguito descritti, a grandi linee, solo quelli più rilevanti per la comprensione della problematica.
Per capire se il metodo scelto e la funzione interpolante trovata sono adatti, occorre rispondere a quattro quesiti di linea generale:
- Quanto è esatto il metodo?
- Quanto è costoso computazionalmente il metodo?
- Quanto è buona la funzione interpolante?
- Quanti punti dati sono necessari per procedere?
Interpolazione lineare[modifica | modifica wikitesto]

Uno dei metodi più semplici è l'interpolazione lineare. Si consideri di voler determinare nell'esempio precedente. Poiché 2.5 è il punto medio fra 2 e 3, è ragionevole individuare come il valore medio fra e : in tal modo si ottiene .
In generale, l'interpolazione lineare per ogni coppia di punti dati consecutivi, denotati e , definisce come funzione interpolante nell'intervallo :
- .
Questa formula può essere interpretata come valutazione della media ponderata.
L'interpolazione lineare è rapida e facile, ma non è molto precisa e porta ad ottenere una funzione non differenziabile nei punti .
La seguente stima dell'errore indica la scarsa precisione dell'interpolazione lineare. Indichiamo con la funzione interpolante e supponiamo che la sia compresa fra e e che sia due volte differenziabile. Allora l'errore dell'interpolazione lineare è
- .
Quindi, l'errore è proporzionale al quadrato della distanza fra i punti dati. Altri metodi, comprese l'interpolazione polinomiale e l'interpolazione spline, descritti di seguito, producono funzioni più lisce ed errori di interpolazione proporzionali a potenze superiori della distanza fra i punti dati, quindi sono preferibili.
Interpolazione polinomiale[modifica | modifica wikitesto]
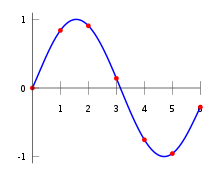
L'interpolazione polinomiale può considerarsi una generalizzazione dell'interpolazione lineare. Mentre l'interpolante lineare è una sequenza di funzioni lineari, nell'interpolazione polinomiale si cerca come interpolante un polinomio di un grado opportuno (grado che nel caso dell'interpolazione lineare sarebbe pari a 1).
Per il problema dato sopra si trova che il seguente polinomio di sesto grado passa attraverso tutti i sette punti:
. Assegnando , troviamo che .
In generale, quando si hanno n punti dati, esiste esattamente un polinomio di grado n−1 che passa attraverso tutti tali punti. L'errore di interpolazione è proporzionale alla distanza fra i punti dati elevata alla potenza n-esima. L'interpolante, inoltre, in quanto polinomio, è illimitatamente differenziabile. L'interpolazione polinomiale, quindi, evita tutte le difficoltà incontrate dalla interpolazione lineare.
Se si riprendono i 4 quesiti visti in precedenza, si vede che l'interpolazione polinomiale presenta alcuni svantaggi. Il calcolo del polinomio d'interpolazione è molto costoso in termini computazionali e l'interpolazione polinomiale non risulta molto esatta nell'intero dominio della funzione; in particolare nei punti estremi dell'intervallo si manifesta il cosiddetto fenomeno di Runge. Questi svantaggi possono essere evitati usando altre interpolazioni, in particolare l'interpolazione spline.
Interpolazione razionale[modifica | modifica wikitesto]
L'interpolazione razionale, simile a quella polinomiale, utilizza delle funzioni razionali
.
I più noti metodi di interpolazione razionale sono
- Bulirsch - Stoer, da non confondere con quello per le equazioni differenziali[1].
- Berrut, un miglioramento del precedente[2]
- Hormann - Floater[3]
Dei tre, l'ultimo non produce mai asintoti e garantisce un modesto errore anche con piccoli intervalli, anche con le funzioni che con i polinomi causano il fenomeno di Runge. Il vantaggio dell'approssimazione razionale è che, ad esempio nella funzione , l'interpolazione polinomiale causa delle forti oscillazioni, soprattutto fuori dai valori tabellati (estrapolazione), mentre la razionale ha meno oscillazioni e coinvolge meno calcoli dell'interpolazione spline, essendo generalmente implementata in per il calcolo dei pesi, da farsi una tantum per i valori tabulati, e per l'interpolazione.
Interpolazione spline[modifica | modifica wikitesto]

Mentre l'interpolazione lineare utilizza una funzione lineare per ciascuno degli intervalli , la interpolazione spline si serve nei suddetti intervalli di polinomi di grado piccolo, scegliendoli in modo che due polinomi successivi si saldino in modo liscio. La funzione che si ottiene con un procedimento di questo genere si chiama funzione spline.
Per esempio, la spline naturale cubica è a tratti cubica, due volte differenziabile e presenta derivata seconda uguale a zero nei punti finali. La spline naturale cubica che interpola i punti nella tabella qui sopra è così definita
La funzione interpolante ottenuta con la interpolazione spline, come quella ottenuta con la interpolazione polinomiale, rispetto a quella ottenuta con l'interpolazione lineare, presenta errori inferiori, è più liscia, risulta più facile da valutare e non soffre del fenomeno di Runge.
Altre forme di interpolazione[modifica | modifica wikitesto]
Si individuano altri procedimenti di interpolazione servendosi di famiglie di interpolanti differenti. Si studiano quindi, per esempio, l'interpolazione razionale, cioè l'interpolazione mediante funzioni razionali e l'interpolazione trigonometrica che si serve di polinomi trigonometrici. La trasformata discreta di Fourier è un caso speciale di interpolazione trigonometrica. Un'altra possibilità interessante consiste nell'utilizzare le cosiddette wavelets.
Quando si dispone di un insieme illimitato di punti dati si può adottare le formula interpolante di Nyquist-Shannon.
Si studia anche l'interpolazione multivariata, attività di interpolazione concernente le funzioni di più variabili reali. I suoi metodi includono interpolazione bilineare e interpolazione bicubica in due dimensioni e interpolazione trilineare in tre dimensioni.
In alcuni ambiti applicativi può accadere di disporre non solo di alcuni valori della funzione che vogliamo interpolare, ma anche di valori della sua derivata. In questi casi si trattano i cosiddetti problemi della interpolazione di Hermite.
Nozioni collegate[modifica | modifica wikitesto]
Si usa il termine estrapolazione per l'attività finalizzata a trovare valori di una funzione reale per valori della che sono al di fuori dell'intervallo dell'asse reale che contiene i punti nei quali sono noti i valori che essa assume.
Nei problemi di regressione o di adattamento di curve (curve fitting) si abbandona il vincolo che impone alla funzione interpolante di passare esattamente per i punti dati e si richiede solo una curva approssimante che si avvicini il più possibile ai punti dati.
Un problema diverso dalla interpolazione, ma strettamente collegato con esso, è l'approssimazione di una funzione complicata mediante una più semplice e che presenti un andamento simile. Supponiamo di conoscere la funzione di partenza , ma che questa sia tanto complessa da non potersi valutare efficientemente. Possiamo allora considerare un determinato insieme dei suoi punti e cercare di interpolarli per individuare una funzione più semplice. Naturalmente quando si utilizzerà la funzione approssimante per calcolare nuovi valori si avranno risultati diversi dagli ottenibili se calcolassimo la funzione originale; tuttavia, in certi ambiti applicativi e in seguito all'adozione di opportuni metodi di interpolazione, il vantaggio della maggiore semplicità e della conseguente maggiore manovrabilità può rendere poco rilevante l'errore.
La teoria dell'approssimazione studia come trovare la migliore approssimazione di una funzione con una funzione che appartiene ad una classe predeterminata e quanto risulta buona una tale funzione approssimante. Naturalmente si incontrano delle limitazioni a quanto una interpolante riesca ad approssimare la funzione originale.
Note[modifica | modifica wikitesto]
- ^ Numerical Recipes in C, II ed, (1992) §3.2 Rational Function Interpolation an Extrapolation (PDF), su nrbook.com.
- ^ Jean–Paul Berrut, Richard Baltensperger, Hans D. Mittelmannin, Recent developments in barycentric rational interpolation (PDF), su plato.asu.edu, 2005. URL consultato il 03.06.2008.
- ^ Michael S. Floater, Kai Hormann, Barycentric rational interpolation with no poles and high rates of approximation (PDF), su cg.in.tu-clausthal.de. URL consultato il 03.06.2008 (archiviato dall'url originale il 16 novembre 2010).
Bibliografia[modifica | modifica wikitesto]
- Rice, Herbert Louis (1899) The theory and practice of interpolation; including mechanical quadrature and other important problems concerned with the tabular values of functions.
- Gibb, David (1915): A course in interpolation and numerical integration for the mathematical laboratory.
- Whittaker, Edmund Taylor; Robinson G (1923): A short course in interpolation.
- Whittaker, Edmund Taylor; Robinson G (1924): The calculus of observations, Blackie & Sons. (capitoli 1-4 per interpolazione polinomiale e capitolo 10 per interpolazione con serie di Fourier).
- Abramowitz, Milton; Stegun, Irene (1972): Handbook of Mathematical Functions, Dover. p.877 (Capitolo 25).
- Comincioli, Valeriano (1990): Analisi numerica. metodi, modelli, applicazioni, Capitolo 3, McGraw-Hill Italia. ISBN 88-386-0646-3
- H. Dym, B. Fritzsche, V. Katsnelson, B. Kirstein eds. (1997): Topics in Interpolation Theory, Birkhäuser, ISBN 3-7643-5723-1
- Kincaid, David; Cheney, Ward (2002): Numerical Analysis (3rd ed.), Chapter 6, Brooks/Cole. ISBN 0-534-38905-8
- Schatzman, Michelle (2002): Numerical Analysis: A Mathematical Introduction, Chapters 4 and 6. Clarendon Press, Oxford. ISBN 0-19-850279-6.
- George M. Phillips (2003): Interpolation and Approximation by Polynomials, Springer, ISBN 0-387-00215-4, pp. 328
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «interpolazione»
Wikizionario contiene il lemma di dizionario «interpolazione» Wikimedia Commons contiene immagini o altri file sull'interpolazione
Wikimedia Commons contiene immagini o altri file sull'interpolazione
Collegamenti esterni[modifica | modifica wikitesto]
- interpolazione, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- (EN) interpolation, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Interpolazione, su MathWorld, Wolfram Research.
- Strumento online per l'interpolazione cubica spline con visualizzazione e codice sorgente JavaScript
| Controllo di autorità | Thesaurus BNCF 30706 · LCCN (EN) sh85067492 · BNF (FR) cb11978011w (data) · J9U (EN, HE) 987007558186905171 |
|---|

















![{\displaystyle \,[x_{a},x_{b}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d2c120eaad932a16500410c65d777e65ab24b8)




![{\displaystyle |f(x)-g(x)|\leq C(x_{b}-x_{a})^{2}\quad {\mbox{dove}}\quad C={\frac {1}{8}}~\max _{y\in [x_{a},x_{b}]}~g''(y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1002cb808deb24579002e518136200fc430987d)







![{\displaystyle \,[x_{k},y_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dbec576174286ca6c11e6c73995269631b59bd6)
![{\displaystyle f(x)=\left\{{\begin{matrix}-0.1522x^{3}+0.9937x,&{\mbox{se }}x\in [0,1],\\-0.01258x^{3}-0.4189x^{2}+1.4126x-0.1396,&{\mbox{se }}x\in [1,2],\\0.1403x^{3}-1.3359x^{2}+3.2467x-1.3623,&{\mbox{se }}x\in [2,3],\\0.1579x^{3}-1.4945x^{2}+3.7225x-1.8381,&{\mbox{se }}x\in [3,4],\\0.05375x^{3}-0.2450x^{2}-1.2756x+4.8259,&{\mbox{se }}x\in [4,5],\\-0.1871x^{3}+3.3673x^{2}-19.3370x+34.9282,&{\mbox{se }}x\in [5,6].\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bd6a2cd797d0a4a1f5b777a7fb3ad5f7062185d)


